Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод наименьших квадратов
Содержание
- 1. Метод наименьших квадратов
- 2. 1. Метод наименьших квадратов.В естествознании, в частности
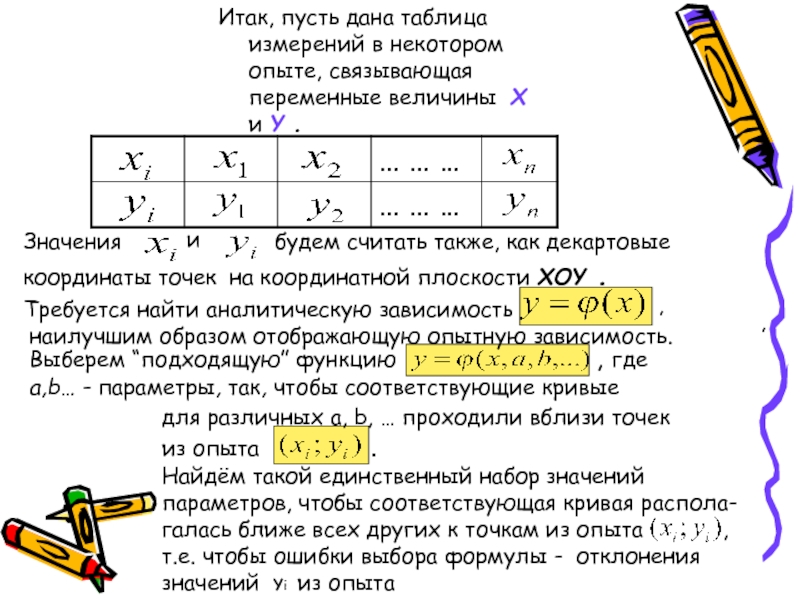
- 3. Итак, пусть дана таблица измерений в некотором
- 4. от соответствующих значений
- 5. Согласно необходимому условию экстремума должна выполнятся следующая
- 6. Пример.Дана таблица измерений.
- 7. Найдем наилучшую из таких прямых, т.е. найдем
- 8. Для решения этой системы составим следующую расширенную
- 9. Найденные значения коэффициентов а и b
- 10. 11457236-1-1-точки из опыта-точки для построения прямойyx-прямая Нетрудно
- 11. 2. Дифференциальные уравнения.Рассмотрим физическую задачу: найти закон
- 12. Определение.Уравнение, связывающее независимую переменную, функцию и ее
- 13. *Решением дифференциального уравнения называется функция
- 14. найти решение
- 15. *Общее решение уравнения (1)- это решение в
- 16. Подставляем y’’ и y в уравнение:т.е. функцияявляется
- 17. Подставляем найденное С в (*):Это и есть
- 18. Для решения уравнения разделим переменные x и
- 19. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3
Итак, пусть дана таблица измерений в некотором опыте, связывающая переменные
величины X и Y .
Значения
и
будем считать также, как
декартовые координаты точек на координатной плоскости XOY .
Требуется найти аналитическую зависимость
наилучшим образом отображающую опытную зависимость.
Выберем “подходящую” функцию , где
а,b… - параметры, так, чтобы соответствующие кривые
для различных a, b, … проходили вблизи точек
из опыта .
Найдём такой единственный набор значений параметров, чтобы соответствующая кривая распола- галась ближе всех других к точкам из опыта ,
т.е. чтобы ошибки выбора формулы - отклонения значений Yi из опыта
,
,
Слайд 4
от соответствующих значений
из
Формулы были наименьшими по абсолютной
величине.Для этого составляется сумма
,
где суммируются квадраты указанных ошибок выбора формулы.
Тогда ошибки выбора будет наименьшими (по абсолютной величине), если наименьшей будет сумма S .
Следовательно, нужно решить задачу на экстремум функции S (a, b, …): найти минимум функции нескольких переменных a, b, … .
Слайд 5
Согласно необходимому условию экстремума должна выполнятся следующая система :
Решение этой
системы даст те значения параметров a, b, …
, при которых функциябудет наилучшей. (Можно доказать, что необходимое условие экстремума при решении таких задач будет и достаточным).
(*)
Слайд 6
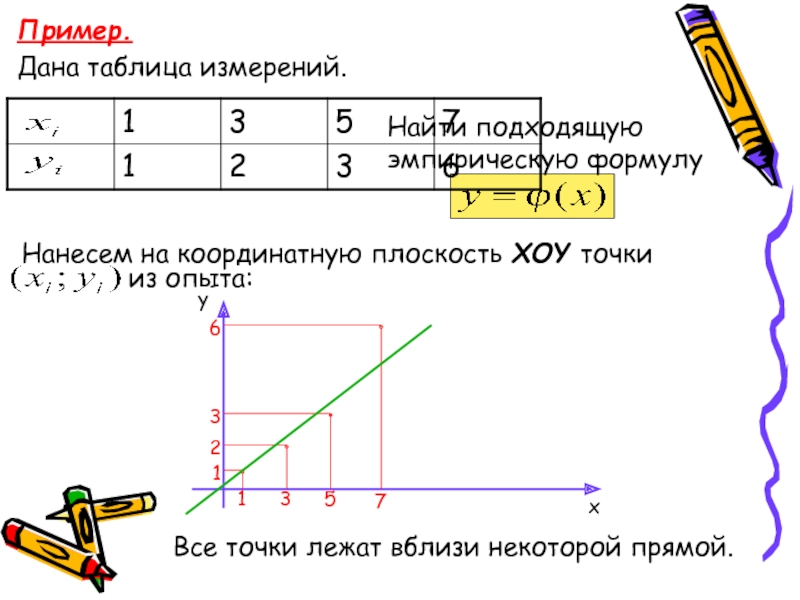
Пример.
Дана таблица измерений.
Найти подходящую эмпирическую формулу
Нанесем на координатную плоскость XOY точки
Все точки лежат вблизи некоторой прямой.
из опыта:
1
3
5
7
1
2
3
6
y
x
Слайд 7
Найдем наилучшую из таких прямых, т.е. найдем линейную зависимость
, наиболее точно описывающую опытную зависимость.
Для такой зависимости система (*) имеет вид:
В нашем случае n=4 и система(**) перепишется :
(**)
(***)
Слайд 8
Для решения этой системы составим следующую расширенную таблицу и заполним
пустые клетки:
Найденные суммы подставляем в систему (***):
Слайд 9
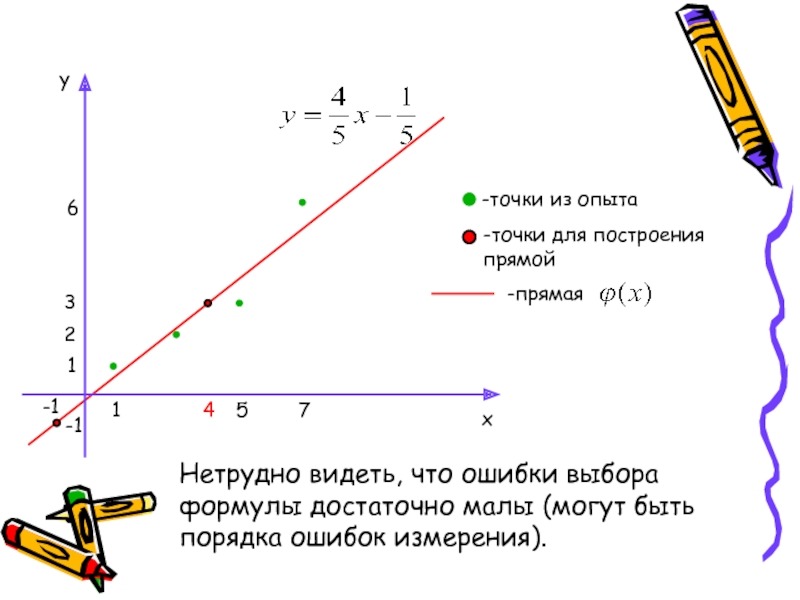
Найденные значения коэффициентов а и b подставляем в уравнение
линейной функции:
По двум точкам строим этупрямую на координатной
плоскости , данной выше:
Слайд 10
1
1
4
5
7
2
3
6
-1
-1
-точки из опыта
-точки для построения прямой
y
x
-прямая
Нетрудно видеть, что ошибки
выбора формулы достаточно малы (могут быть порядка ошибок измерения).
Слайд 112. Дифференциальные уравнения.
Рассмотрим физическую задачу: найти закон прямолинейного движения, при
котором в каждый момент времени путь в 2 раза больше
скорости движения.Путь S(f) – путь, пройденный к моменту t
V(f)- скорость движения
, тогда S=2S’
Решение этого дифференциального уравнения, в которое входит производная, дает искомый закон движения S(t) .
Слайд 12Определение.
Уравнение, связывающее независимую переменную, функцию и ее производные или дифференциалы
различных порядков, называются обыкновенным дифференциальным уравнением.
* Порядком дифференциального уравнения
называется порядок старшей производной, входящей в уравнение.-первого порядка
-второго порядка
-третьего порядка и т.д.
Слайд 13
*Решением дифференциального уравнения называется функция
, удовлетворяющая этому уравнению.
Нахождение этого решения называется
интегрированием дифференциального уравнения.*Если решение уравнения получено в неявном виде
, то оно называется интегралом уравнения.
*Задача Коши.
Задача Коши для уравнения
ставится таким образом: среди всех решений уравнения (1)
(1)
Слайд 14 найти решение
, удовлетворяющее системе следующих условий:
(2)
где
- заданные числа
Эти
условия (2) называются начальными условиями, а соответствующее решение y = y(x) - частным решением уравнения (1).
,
Слайд 15
*Общее решение уравнения (1)- это решение в виде
зависящее от
n
произвольных постоянных
Частные решения уравнения (1) также могут быть получены
из общего решения при некоторых числовых значениях констант Пример.
1.Показать что функция
есть решение
уравнения
Найдем y’’:
Слайд 16
Подставляем y’’ и y в уравнение:
т.е. функция
является решением исходного дифференциального
уравнения.
2.Общий интеграл дифференциального уравнения
имеет вид
(*)
Найти его
частный интеграл, удовлетворяющий начальному условию Найдем значение С, соответствующее искомому частному интегралу, подставив в общий интеграл (*) заданные начальные условия.
У нас
, тогда
, (с – const)