Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы и Системы Поддержки Принятия Решений Methods and Systems for
Содержание
- 1. Методы и Системы Поддержки Принятия Решений Methods and Systems for
- 2. Реализация FMAVT: В Основе – Аддитивная модель
- 3. FMAVT A(x) – ф-я принадл. g(x)=x- Y1- центр тяжести
- 4. FMAA (Fuzzy-MAA)Подход к реализации ранжирования V(ai) на
- 5. Базовый алгоритм MAA (general model)i =(ai) = f(C(ai),w) (1); Sik – Событие ранга, i,k=1,…,n.
- 6. FMAA: Fuzzy MAAНечеткое число Z: normal convex
- 7. FMAA: Fuzzy MAAi =(ai) = f(C(ai),w) (1); ij =i - j :
- 8. Ранжирование в FMAAРанжирование/выбор альтернатив {i=1,…n} в FMAA
- 9. Задание весов в FMAAMAVT/MAUT – коэффициенты масштабирования
- 10. FMAA (-V): setting criterion values, weights
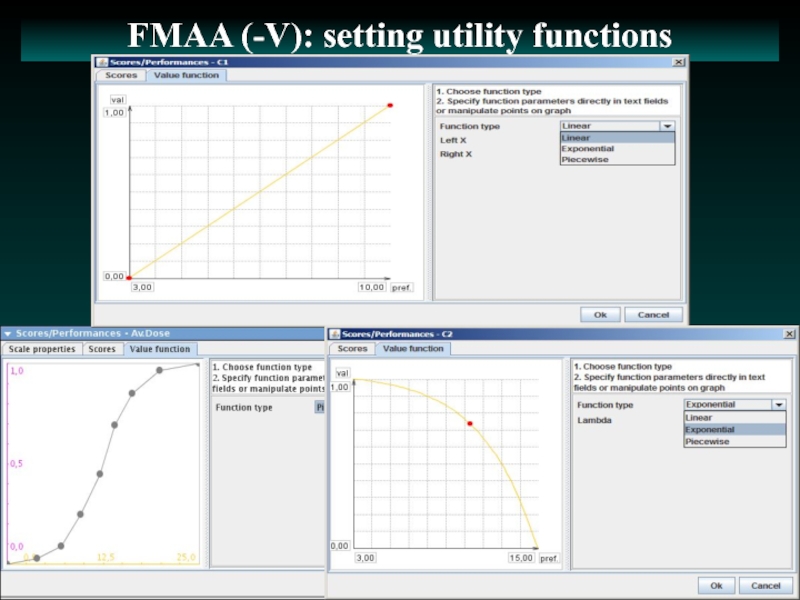
- 11. FMAA (-V): setting utility functions
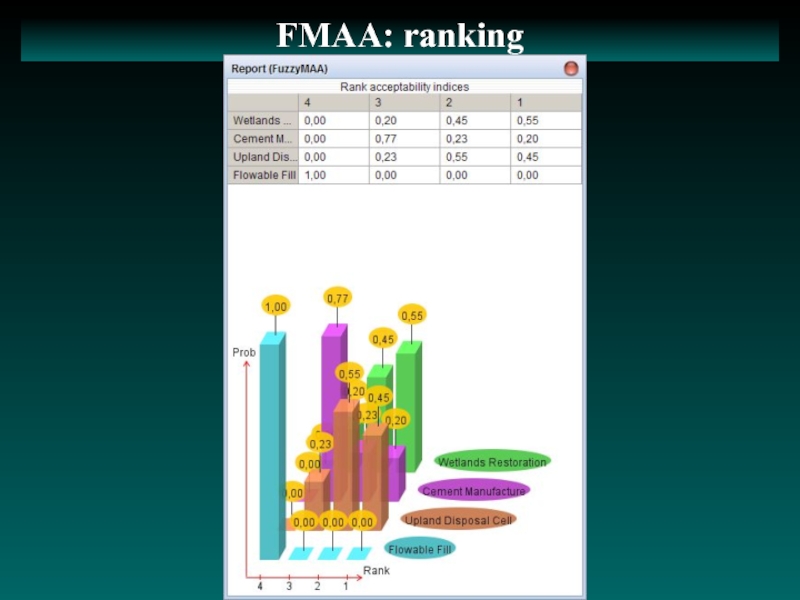
- 12. FMAA: ranking
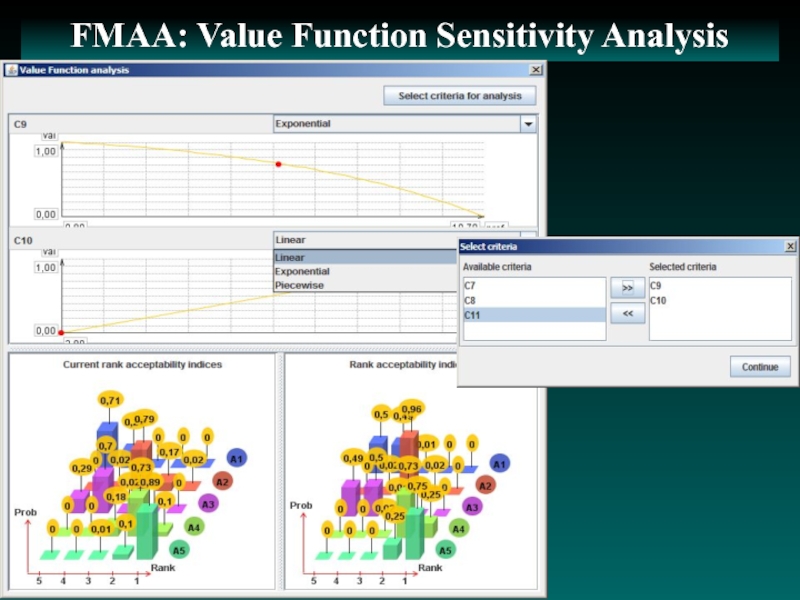
- 13. FMAA: Value Function Sensitivity Analysis
- 14. Conclusion FMAA is an approaches to MAA
- 15. THANK YOUwww.deesoft.ruyatsalo@gmail.com
- 16. Скачать презентанцию
Реализация FMAVT: В Основе – Аддитивная модель MAVT:V(a) = w1 V1(a1) +…+ wm Vm(am ), wj > 0,- Задание нечетких значений/чисел для критериев aj=Cj(ai) и альтернатив ai
Слайды и текст этой презентации
Слайд 1Методы и Системы Поддержки Принятия Решений Methods and Systems for Decision-Making
Support
множеств/чисел (Fuzzy Sets/ Numbers): F-MAVT, FMAA
Слайд 2Реализация FMAVT:
В Основе – Аддитивная модель MAVT:
V(a) = w1
V1(a1) +…+ wm Vm(am ), wj > 0,
- Задание
нечетких значений/чисел длякритериев aj=Cj(ai) и альтернатив ai
(см. формы для задания нечетких чисел в DecernsMCDA)
Задание частных функций полезности Vj(х) – как и функций ценности Vj(х) в MAVT;
Задание весовых коэффициентов в виде нечетких чисел (~как в MAUT; на основе swing процедур, модифицированных для FMAVT)
FMAVT (= Fuzzy-MAVT)
Слайд 3FMAVT
A(x) – ф-я принадл.
g(x)=x- Y1- центр тяжести (среднее)
Проблема ранжирования нечетких
чисел
V(ai) , i=1,…,n
Использование различных методов ранжиования
Слайд 4FMAA (Fuzzy-MAA)
Подход к реализации ранжирования V(ai) на основе методологии MAA:
Событие
ранга (Rank Event):
Sik={Альтернатива ai имеет ранг k}, i,k=1,…,n.
μ(Sik) Индекс
Приемлемости Ранга (ИПР)(rank acceptability index): = Мера события Sik
Как вычислить меру Sik
= аналитический подход + численные методы
1) FMAA – “fuzzy approach”: μ(Sik)
2) ProMAA – “probabilistic approach”: P(Sik)
Слайд 5Базовый алгоритм MAA
(general model)
i =(ai) = f(C(ai),w) (1); Sik
– Событие ранга, i,k=1,…,n.
Слайд 6FMAA: Fuzzy MAA
Нечеткое число Z: normal convex bounded fuzzy set
in
Степень неотрицательности нечеткого числа z
- (непрерывная)
функция принадлежности
Слайд 8Ранжирование в FMAA
Ранжирование/выбор альтернатив
{i=1,…n} в FMAA базируется на анализе
матрицы {μ(i,k)}, i,k=1,…,n.
Интегральный индекс приемлемости альтернативы ai (the ‘holistic acceptability
indices’) Ri, i=1,…,n, может применяться:(however, the recommendations concerning implementation of such a secondary ranking as a decision rule are restricted)
Слайд 9Задание весов в FMAA
MAVT/MAUT – коэффициенты масштабирования (scaling factors);
Swing
метод: (+ задание диапазона изменения весового коэф.)
FMAA (swing):
w1=1
– для наиболее значимого критерия (C1), в соотв со свинг процедурами); 
Слайд 14Conclusion
FMAA is an approaches to MAA
which treat uncertainties of
criteria and weights with the use of Fuzzy Numbers - FMAA
method is based on analytical approach/ model to Rank Event formation and numerical calculation of Rank Acceptability Indices - FMAA, F-MAVT have been realized in DecernsSDSS (DecernsMCDA)
