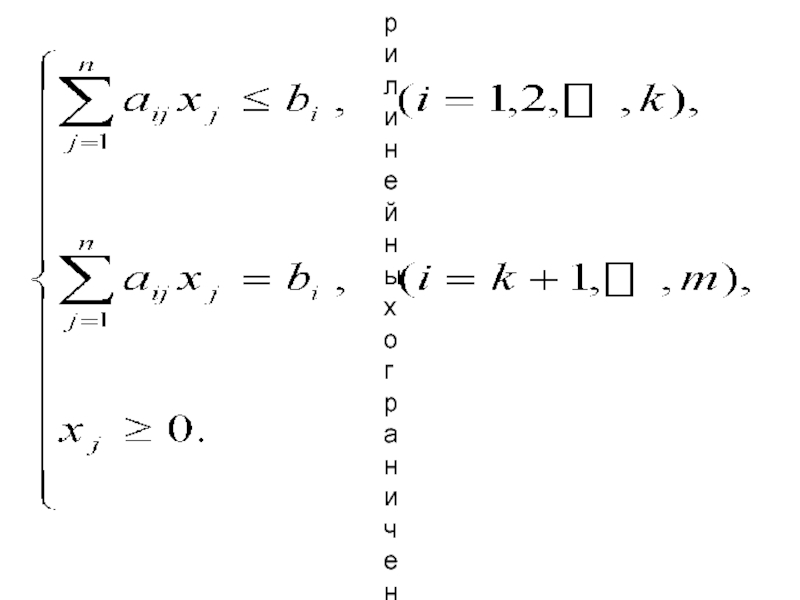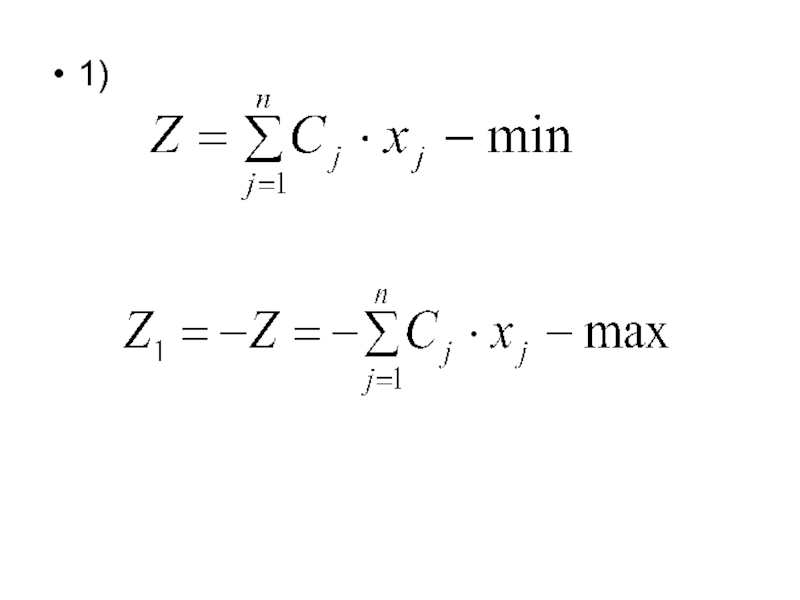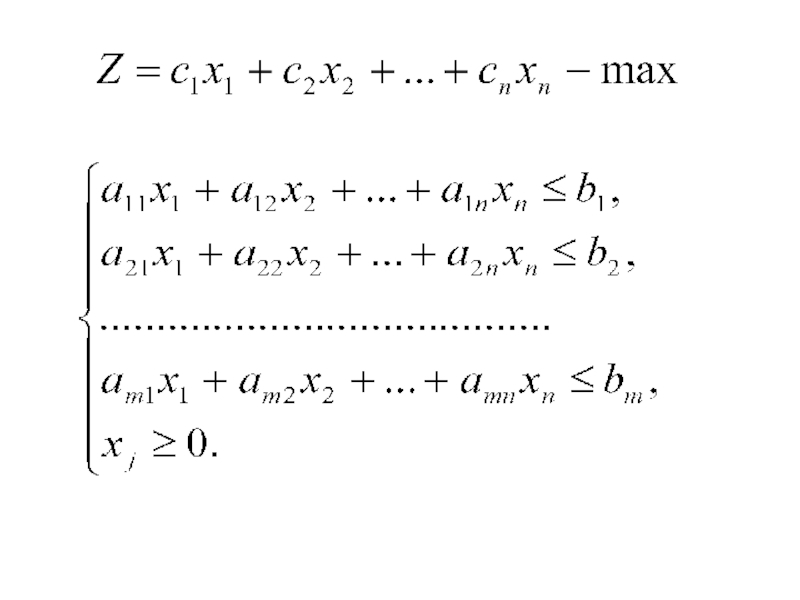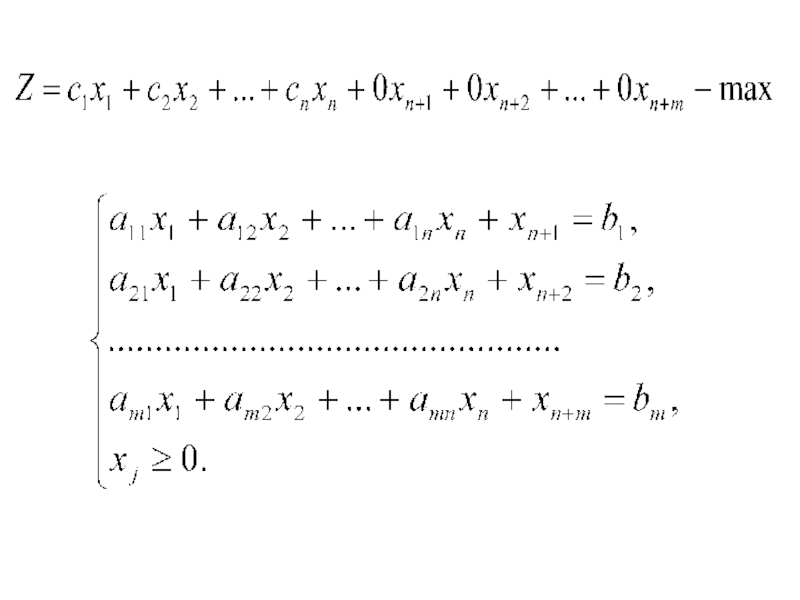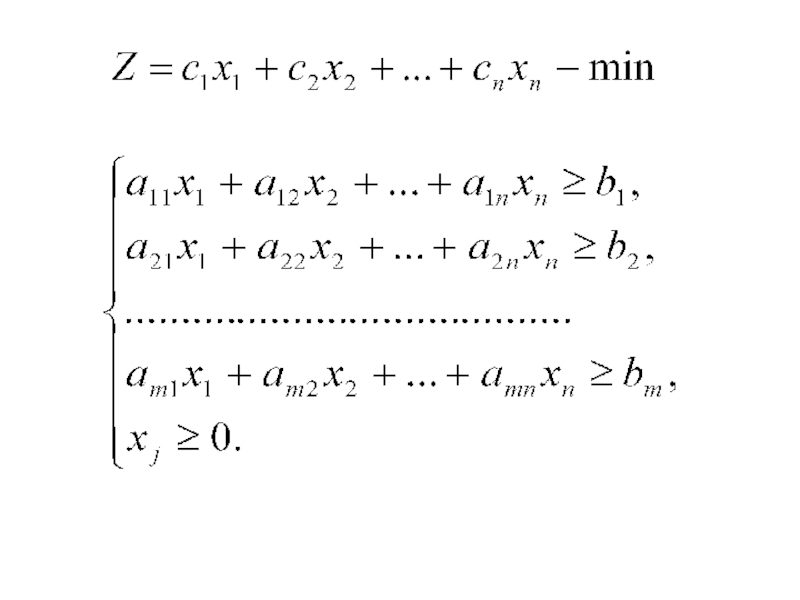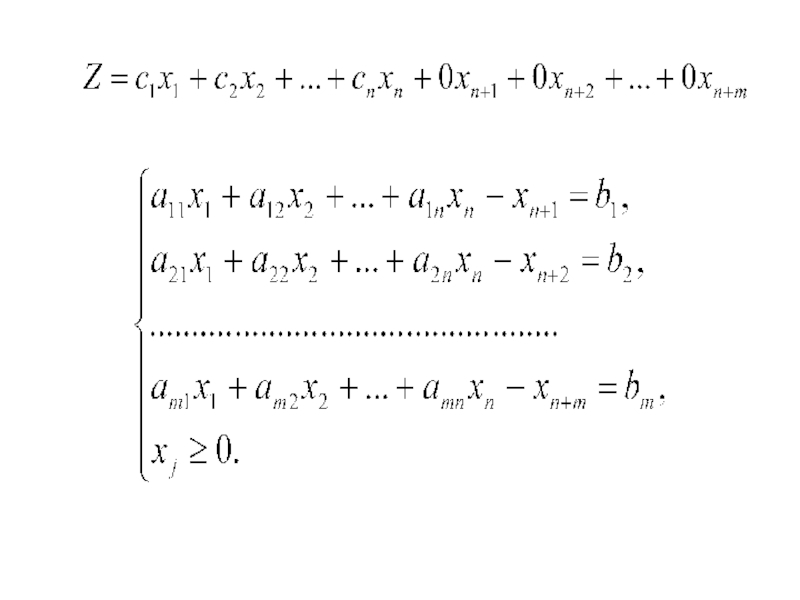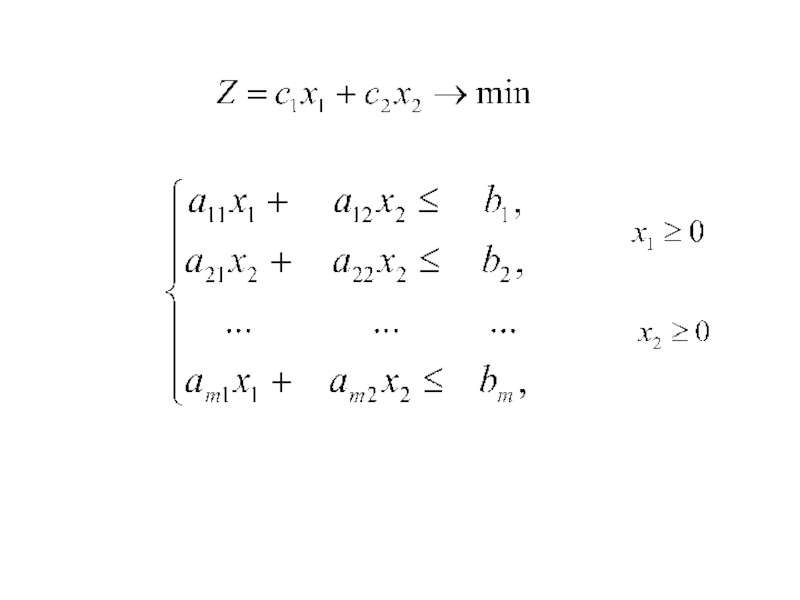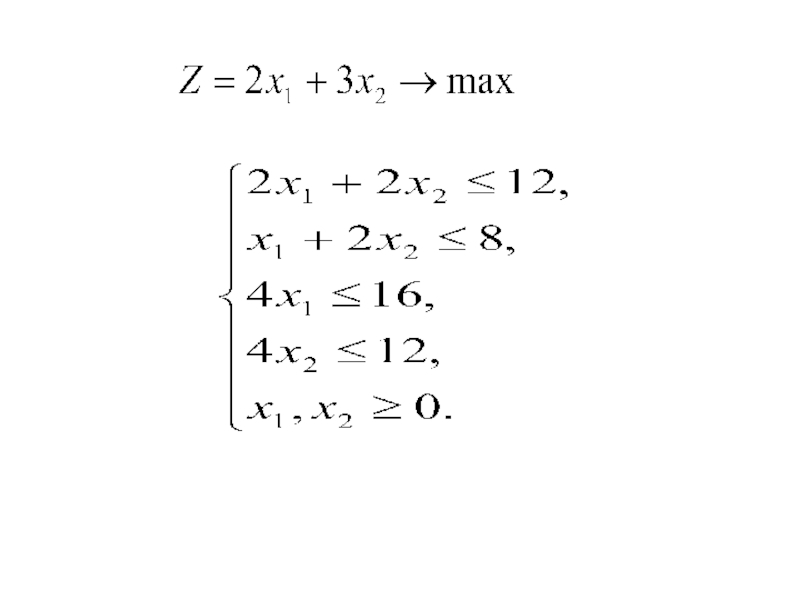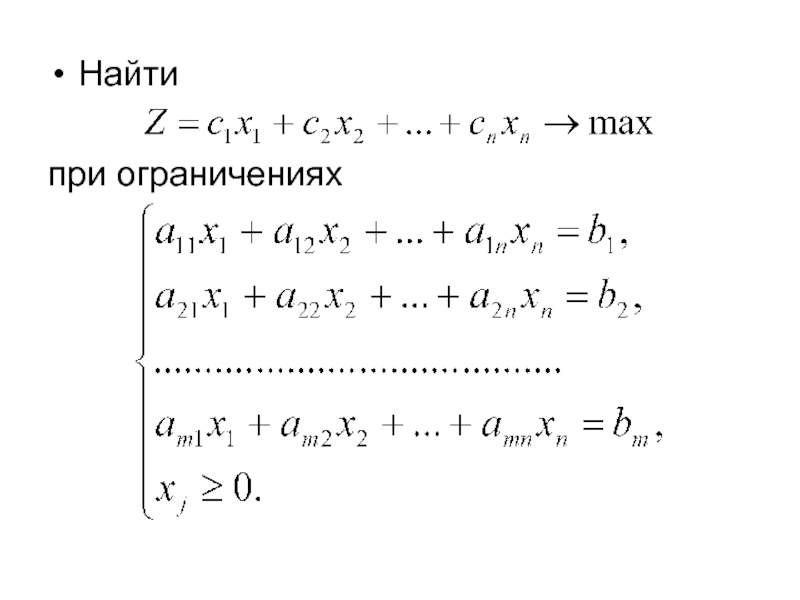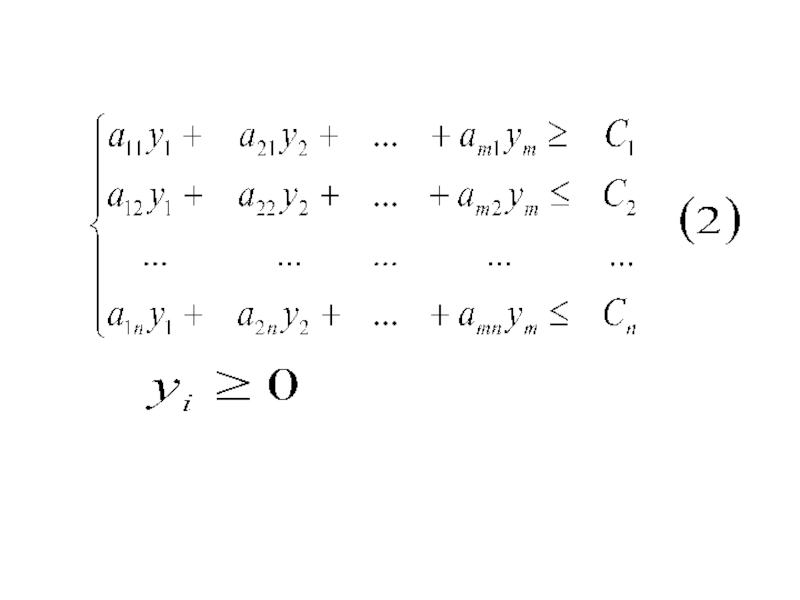Слайд 21. Введение
2. Линейное программирование.
3. Определение опорного плана. Выпуклые множества.
4. Свойства решений задачи линейного программирования.
5. Графический метод решения ЗЛП.
6.
Неединственность оптимального решения.
7. Симплексный метод решения ЗЛП.
8. Метод искусственного базиса.
9. Двойственность в линейном программировании
10. Правила составления двойственных задач.
11. Транспортная задача.
12. Построение первоначального опорного плана.
13. Методы северо-западного угла и минимальной стоимости.
14. Метод потенциалов.
15. Открытая модель транспортной задачи.
Слайд 3 Введение
Данный курс охватывает достаточно обширный круг математических методов
и моделей, в том числе и моделей оптимизации, которые нашли
широкое применение в экономической науке.
Слайд 4 Например, в модели поведения потребителя предполагается, что он ищет максимум
полезности.
Модели фирмы основаны на предпосылке максимума прибыли для предпринимателя.
Слайд 5 Модели рынка - на предпосылке оптимальных стратегий участников обмена.
Модели
общего равновесия – на предпосылке цен оптимального плана.
Модели воспроизводства – на предпосылке оптимального роста.
Слайд 6 При изучении дисциплины
“ ЭММ и модели “ особое внимание
уделяется не только изучению известных моделей и методов моделирования, но
и анализу этих моделей, применению их на практике с учетом конкретных условий.
Слайд 7 Экономико-математическое моделирование, является одним из эффективных
методов описания сложных социально-экономических объектов и процессов, позволяющих овладеть искусством
принятия управленческих и инвестиционно-финансовых решений, распределения и оптимизации ресурсов, анализа и обработки данных и прогнозирования последствий.
Слайд 8Экономико-математические методы- обобщающее название комплекса экономических и математических научных дисциплин,
объединенных для изучения социально-экономических систем и процессов.
Слайд 9 Раздел математики, который занимается решением задач о нахождении
экстремума функции на множествах, определяемых линейными или нелинейными ограничениями, называется
математическим программированием.
Слайд 10 Математическое программирование включает такие разделы как
линейное
программирование
нелинейное программирование
динамическое программирование
теория игр.
Слайд 11Линейное программирование. Разработка моделей линейного программирования.
Слайд 12Линейное программирование- это наука о методах исследования и отыскания наибольшего
и наименьшего значений линейной функции ( которую будем называть целевой
функцией) на неизвестные которой наложены линейные ограничения.
Слайд 13 Разработка моделей линейного программирования включает следующие основные этапы:
- определение переменных задачи,
-представление ее ограничений в виде линейных уравнений или неравенств;
- задание линейной целевой функции подлежащей минимизации или максимизации.
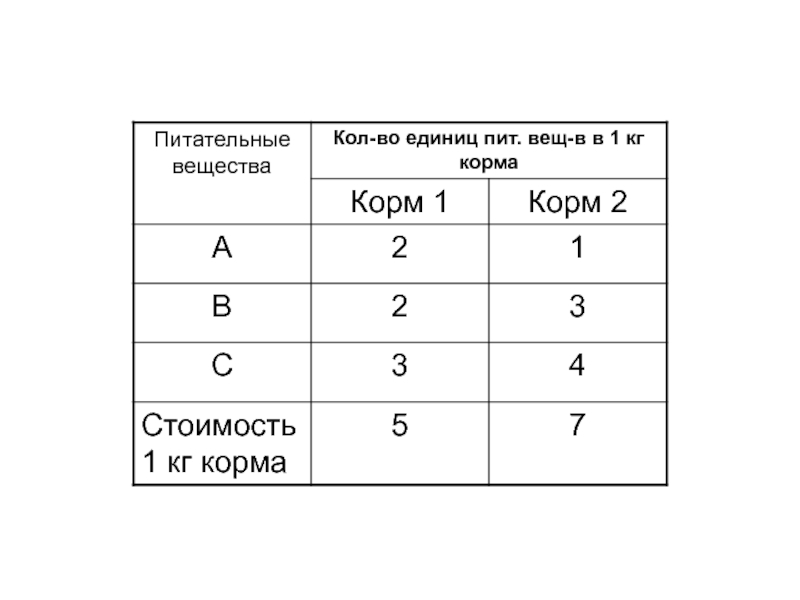
Слайд 15В ОТК некоторой фирмы работают контролеры 1 и 2 разрядов.
Норма выработки ОТК за 8 часовой рабочий день составляет неменее
1800 изделий. Контролер 1 разряда проверяет
25 изд./час , причем не ошибается в 98% случаев. Контролер 2 разряда проверяет
15 изд./час, его точность- 95%. Заработная плата контролера 1 разряда равна
4 д.е./час, контролер 2 разряда получает 3. д.е./час. При каждой ошибке контролера фирма несет убыток в размере 2 д.е.
Слайд 16Фирма может использовать 8 контролеров 1 разряда и 10 контролеров
2 разряда. Руководство фирмы хочет определить оптимальный состав ОТК, при
котором общие затраты на контроль будут минимальны.
Слайд 19 Общей задачей линейного программирования называется задача, которая
состоит в определении max (min) значения функции
при условиях
Слайд 21Стандартной (симметричной) задачей ЛП наз-ся задача , которая состоитв определении
оптимального значения функции
при условиях
Слайд 23 Основной (или канонической) задачей линейного программирования называется задача, которая
состоит в определении оптимального значения функции
при выполнении условий
Слайд 25 Совокупность чисел
удовлетворяющих ограничениям задачи называется допустимым решением (или планом).
Слайд 26 Оптимальным решением ЗЛП называют допустимое решение
при котором целевая функция принимает максимальное или минимальное значение.
Слайд 27Совокупность чисел
удовлетворяющих условию
наз-ся оптимальным
Слайд 31соответствует единственное решение
уравнения
(2)
и неравенства (3)
Слайд 32И наоборот каждому решению
уравнения (2) и неравенства
(3)
соответствует единственное решение
неравенства (1)
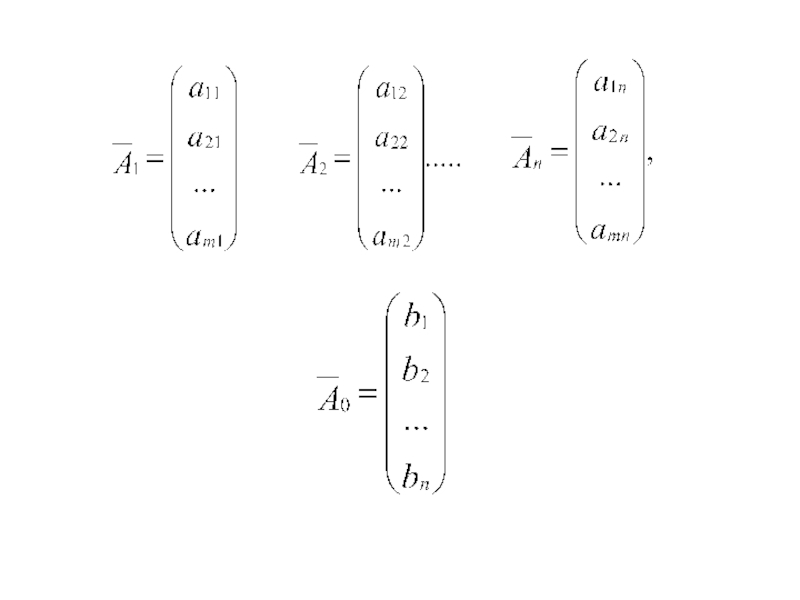
Слайд 37Векторная форма записи
задачи линейного программирования.
Слайд 38Минимизировать линейную функцию
при ограничениях
(*) , ,
где ,
Слайд 40Матричная форма записи задачи линейного программирования.
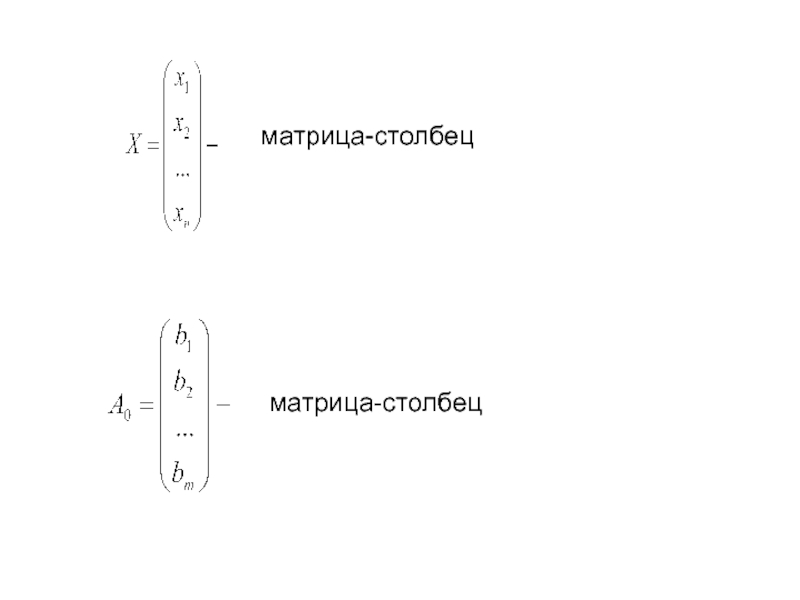
Слайд 41Минимизировать линейную функцию
при ограничениях
где
- матрица-строка,
матрица-системы
Слайд 43Определение опорного плана. Выпуклые множества.
называется опорным, если векторы
, входящие в разложение (*) с положительными коэффициентами являются линейно независимыми.
Слайд 45Выпуклые множества
Пусть на плоскости заданы
две
точки
определяющие отрезок
Слайд 47 Точка ,для которой выполняется условие
,
где , ,
называется выпуклой линейной комбинацией
точек .
Слайд 48Точки называются угловыми или
крайними точками отрезка
.
Угловая точка не может быть
представлена как выпуклая линейная
комбинация двух других точек отрезка.
Слайд 49
Пусть имеется точек
-мерного пространства, то точка – выпуклая линейная комбинация, если выполняется условие
Слайд 50 Множество точек называется выпуклым, если оно вместе с
любыми двумя точками содержит и отрезок их соединяющий.
Слайд 51 Геометрический смысл:
Множеству вместе с его
двумя произвольными точками полностью принадлежит и прямолинейный отрезок, их соединяющий.
Слайд 52 Точка множества называется граничной, если любой шар сколь угодно
малого радиуса с центром в этой точке содержит как точки
принадлежащие множеству, так и точки не принадлежащие ему.
Граничные точки множества образуют его границу.
Замкнутое - множество, содержащее все свои граничные точки.
Слайд 53В треугольнике угловые точки –вершины.
Угловые точки круга- точки окружности,
которая его ограничивает.
Выпуклое множество может иметь конечное или бесконечное число
угловых точек.
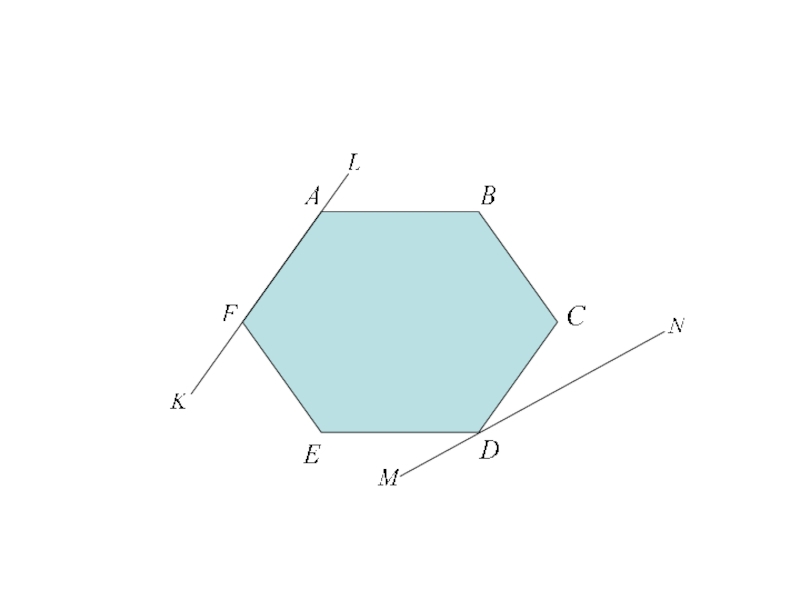
Слайд 54 Выпуклый многоугольник - выпуклое замкнутое ограниченное множество на
плоскости, имеющее конечное число угловых точек.
Опорная прямая выпуклого
многоугольника - прямая, имеющая с многоугольником расположенным по одну сторону от ее, хотя бы одну общую точку.
Слайд 56Свойства решений задачи линейного программирования.
Слайд 57 Теорема 1:
Множество всех планов задачи линейного программирования
выпукло.
Слайд 58 Теорема 2:
Линейная функция задачи линейного программирования
достигает своего оптимального значения в угловой вершине многоугольника решений. Если
линейная функция принимает оптимальное значение более, чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.
Слайд 59 Теорема 3:
Если известно, что система векторов
в разложении
линейно независима и
такова, что,
где все , то точка является
угловой точкой многоугольника решений.
– n-мерный вектор; n-k – компонент 0.
– угловая точка
многоугольника решений, то векторы в
разложении, соответствующие
положительным , являются линейно
независимыми.
Слайд 61Следствие 1:
Так как векторы
имеют размерность
, то угловая точка многоугольника решений имеет не более чем положительных компонент
Слайд 62Следствие 2:
Каждой угловой точке многоугольника
решений соответствует
линейно независимых векторов системы
Слайд 64 Графический метод основан на геометрической интерпретации задачи линейного
программирования.
Слайд 65Найти минимальное решение функции
Слайд 66 Предположим, что эта система совместна (имеет хотя бы
одно решение) и ее многоугольник решений ограничен. Линейная функция
при фиксированных значениях является уравнением прямой .
Слайд 67 Построим многоугольник решений системы ограничений и график линейной
функции
. Тогда задачу линейного программирования можно сформулировать так: найти точку многоугольника решений, в которой прямая
опорная и функция при этом достигает минимума.
возрастают в
направлении
,
поэтому прямую передвигаем
параллельно самой себе в направлении
Слайд 70 Прямая становится опорной в (∙) и
.
min значение функция принимает
в (∙)
, координаты которой находим,
решая систему уравнений прямых AE и ED.
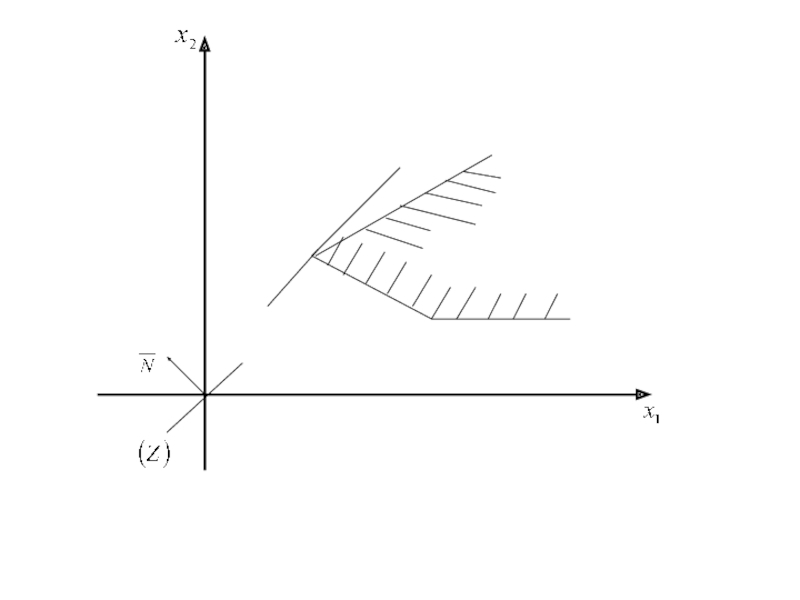
Слайд 75Неединственность оптимального решения. Неограниченный оптимум.
Слайд 76 Неединственность оптимального решения.
Для некоторых задач линейного
программирования может существовать несколько допустимых решений со значением целевой функции
равной оптимальному значению задачи. В таких случаях все эти допустимые решения оптимальны и говорят, что задача линейного программирования имеет альтернативные оптимальные решения.
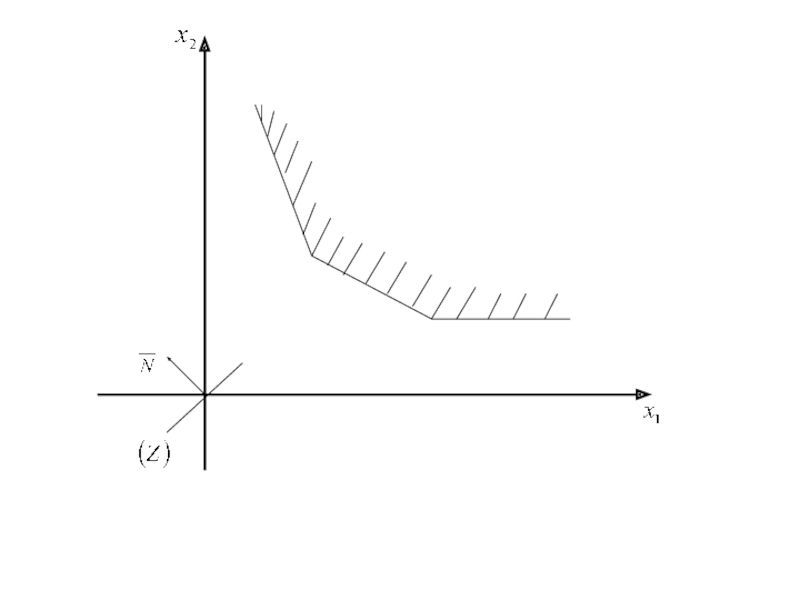
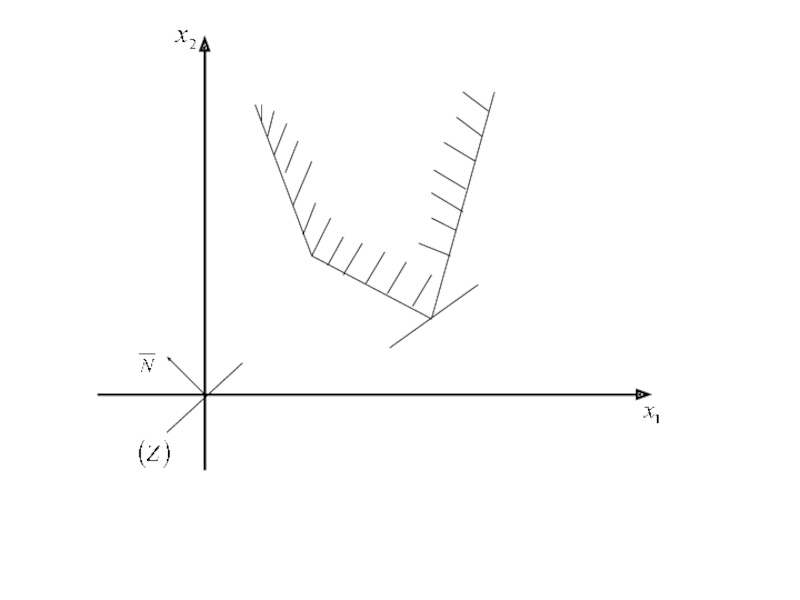
Слайд 77 Неограниченный оптимум.
Для некоторых задач линейного
программирования
не существует оптимального
решения, то есть для любого допустимого
решения
можно найти другое допустимое
решение, которому соответствует лучшее
значение целевой функции.
В этом случае удаление от начала координат
вызывает рост целевой функции и
если не существует конечного оптимума,
говорят что задача линейного
программирования имеет неограниченный
оптимум.
Слайд 78 На практике такая ситуация не встречается, так как
иначе можно было бы получить бесконечный доход при конечном запасе
ресурсов.
Если в практической задаче такое решение получено, это значит, что на этапе построения модели пропущено одно (или несколько) из ограничений.
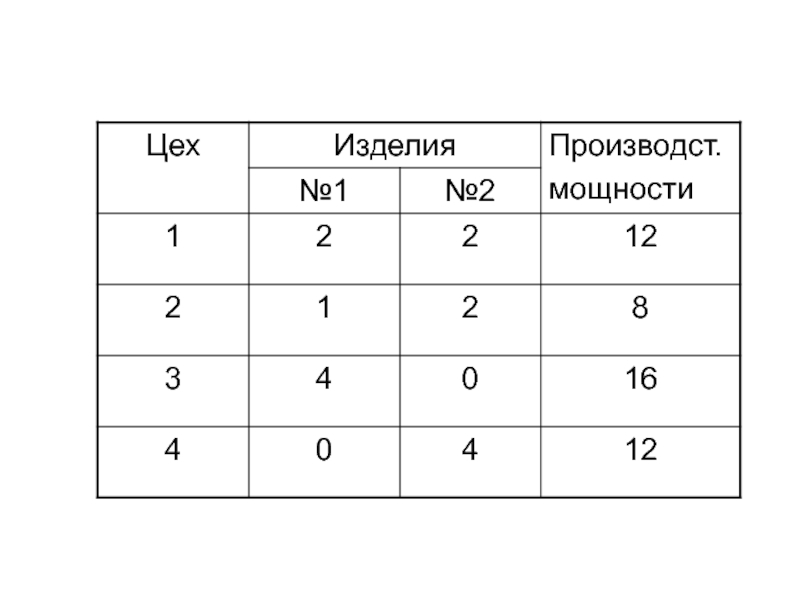
Слайд 80На предприятии, в состав которого
входят 4 производственных цеха,
изготовляются два изделия.
Производственные
мощности цехов (в
часах) в расчете на сутки соответственно
составляют: 12, 8,
16, 12.
Нормы времени, необходимого для
изготовления единицы изделия №1 и №2
в соответствующих цехах, приведем в
таблице.
Слайд 82Прибыль от продажи единицы изделия №1 составляет 2 тыс.ед, а
единицы изделия №2 составляет 3 тыс.ед. Следует выбрать тот из
возможных вариантов производственного плана, при котором обеспечивается max прибыль
Слайд 85 Из свойств решений задачи ЛП следует, что существует
такая угловая точка (вершина) многогранника решений, в которой целевая функция
достигает своего наибольшего (наименьшего) значения.
Слайд 86 Каждой угловой точке многогранника решений соответствует опорный план,
а каждый опорный план определяется системой m линейно независимых векторов,
содержащихся в данной системе из n векторов .
Слайд 87 Для отыскания оптимального плана необходимо исследовать только опорные
планы. Количество опорных планов, содержащихся в данной задаче, определим через
Слайд 89Условие оптимальности опорного плана.
1.При решении задачи ЛП, решаемой на отыскание
минимального значения целевой функции, неравенства
являются условием оптимальности
Слайд 90 Если для некоторых
j,
то можно перейти от исходного плана к новому опорному, при котором значение целевой функции будет меньше, чем предыдущее. Этот переход осуществляется исключением из исходного базиса какого-нибудь вектора и введением в базис нового.
Слайд 91
2. При решении задачи ЛП, решаемой на отыскание максимального значения
целевой функции, неравенства
являются условием оптимальности
Слайд 92 Если для некоторых j,
то можно перейти от исходного плана к новому опорному, при
котором значение целевой функции будет больше, чем предыдущее. Этот переход осуществляется исключением из исходного базиса какого-нибудь вектора и введением в базис нового.
Слайд 93 Неединственность оптимума.
Если в оптимальной таблице небазисный
вектор имеет нулевую оценку, то задача ЛП будет иметь неединственное
решение. Можно перейти к другой оптимальной таблице с другим решением, но значение целевой функции будет оставаться прежним. График целевой функции параллелен той прямой, на которой лежит точка min или max.
Слайд 94 Неограниченность оптимума.
Говорят, что задача
ЛП имеет неограниченный оптимум, если у нее нет конечного оптимального
решения.
В таком случае
(для задачи максимизации),
(для задачи минимизации).
Слайд 95 Вырожденность и зацикливание
При рассмотрении симплекс-метода предполагаем,
что все . Если какое-то
, то такой план задачи в качестве базисной переменной содержит нулевое значения, т.к. план называется вырожденным.
Слайд 96Правило для устранения зацикливания
Если на каком-либо этапе расчета
возникает неопределенность в выборе разрешающей строчки, т.е. 2 и более
одинаковых min отношений, то следует выбрать ту строку, для которой отношение элементов следующего столбца к разрешающему является наименьшим. Если снова оказываются равными минимальные отношения, то выбирают следующий столбец и так до тех пор, пока разрешающая строка не определится однозначно.
Слайд 98Двойственный симплекс-метод заключается в построении оптимального недопустимого плана с последующим
преобразованием его в допустимый, не нарушая оптимальности
Слайд 99Алгоритм двойственного симплекс-метода.
Слайд 1001. Выбирают разрешающую строку по наибольшему по абсолютной величине отрицательному
элементу столбца правых частей.
Слайд 1012.Выбирают разрешающий столбец по наименьшему по абсолютной величине отношению элементов
строки к отрицательным элементам разрешающей строки
Слайд 1023.Пересчитывают симплексную таблицу по правилам обычного симплекс-метода.
Слайд 1034. Решение проверяют на оптимальность. Признаком получения допустимого оптимального решения
является отсутствие в столбце правых частей отрицательных элементов.
Слайд 1051.Если в разрешающей строке нет ни одного отрицательного элемента, задача
неразрешима.
2.Если ограничения задачи заданы неравенствами типа «≥», двойственный симплекс-метод позволяет
избавиться от необходимости введения искусственных переменных.
Слайд 107 Этот метод применяется в тех случаях, когда система
ограничений содержит неравенство типа «≥» или равенство и при этом
явно не видно базисных векторов
Слайд 108 Если ограничения задачи ЛП можно преобразовать к виду
,
то всегда существует базис из единичных векторов.
Существуют задачи ЛП, которые имеют решения, но не имеют единичных векторов и ограничения не приводятся к указанному виду. В этом случае для решения задач применяется метод искусственного базиса.
и система ограничений не содержит единичную матрицу.
Чтобы получить единичную матрицу к каждому равенству прибавим по одной переменной
,
которые назовем искусственными и рассмотрим расширенную задачу
Слайд 111Найти
Величина M достаточно большое положительное число.
Слайд 113Найти
Величина M достаточно малое отрицательное число.
Слайд 114 Для отыскания оптимального плана исходной задачи используют теорему:
если в оптимальном плане
расширенной задачи искусственные
переменные ,то план
является оптимальным планом для исходной задачи.
Слайд 115 Применение симплекс-метода к расширенной задаче обеспечивает построение плана,
в котором все искусственные переменные равны нулю.
Если
первоначальная задача не обладает планами, то оптимальное решение расширенной задачи содержит, по крайней мере, хотя бы одну положительную искусственную переменную.
Слайд 116Двойственность в линейном программировании.
Слайд 117 С каждой ЗЛП тесно связана другая линейная задача, называемая
двойственной.
Слайд 118 Экономическая интерпретация
этих задач следующая:
- исходная задача: сколько и какой продукции
, необходимо
произвести, чтобы при заданных
стоимостях единицы продукции и размерах имеющихся ресурсов
максимизировать выпуск продукции в
стоимостном выражении;
Слайд 119- двойственная задача: какова должна
быть цена единицы каждого из
ресурсов,
чтобы при заданных количествах ресурсов
и величинах стоимости единицы
продукции
минимизировать общую стоимость
затрат
Слайд 120 Первоначальный опорный план
составляется, так же как и
при решении ЗЛП
симплекс-методом. Обозначим через
количество единиц j-й продукции.
За единицу стоимости ресурсов примем
единицу стоимости выпускаемой продукции.
Обозначим через стоимость единицы
i-го ресурса.
Слайд 121Тогда стоимость всех затраченных
ресурсов, идущих на изготовление
единицы j-й продукции равна
где - количество единиц i-го ресурса,
которое
идет на производства 1ед. j-ой
продукции
Слайд 122
Стоимость затраченных ресурсов не
может быть меньше стоимости
окончательного продукта
Слайд 123 Стоимость всех имеющихся ресурсов
выразится величиной
Слайд 124 Итак, двойственную задачу сформулируем следующим образом:
найти
вектор
который удовлетворяет ограничениям
доставляет минимальное значение
линейной функции
Слайд 127
Каждая из задач двойственной пары
фактически является ЗЛП и
может
быть решена независимо одна от другой.
Однако при определении
симплексным
методом оптимального плана одной из
задач тем самым находится решение и
другой задачи.
Слайд 128 Связь между оптимальными планами пары двойственных задач устанавливает
Теорема двойственности:
Если из пары двойственных задач одна обладает
оптимальным планом, то и другая имеет решение, причем для экстремальных значений линейных функций выполняется соотношение
Если линейная функция одной из задач неограниченна, то другая не имеет решения.
Слайд 129Правила составления двойственных задач.
Слайд 130 1. Целевая функция исходной задачи задается на максимум,
целевая функция двойственной – на минимум.
Слайд 1312. Матрица , составленная из
коэффициентов (при неизвестных в
системе
ограничениях) при неизвестных в исходной
задаче, и матрица получаются друг из
друга транспонированием.
Слайд 132 3. Число переменных ( ) в двойственной задаче
равно числу ограничений исходной задачи. Число ограничений двойственной задачи равно
числу переменных исходной задачи.
Слайд 1334. Коэффициентами при неизвестных в целевой функции двойственной задачи являются
правые части системы ограничений исходной задачи.
Правыми частями
в системе ограничений двойственной задачи являются коэффициенты при неизвестных целевой функции исходной задачи.
Слайд 1345. Если переменная исходной задачи может принимать
только положительные значения, то j – ое условие двойственной задачи
является неравенством вида ≥.
Слайд 1356.Если переменная может принимать как положительные так
и отрицательные значения, то j – ое ограничение у двойственной
задачи представляет собой уравнение.
Слайд 1367. Если i - ое ограничение исходной задачи является неравенством
вида «≤», то двойственной задачи может принимать
только положительное значение.
Если i - ое ограничение исходной задачи является равенством, то двойственной задачи может принимать как положительные, так и отрицательные значения.
Слайд 1378. Если исходная задача имеет ограничения вида «≤» и все
, то двойственная задача имеет
ограничения «≥», и все .
Если в исходной задаче встречаются неравенства разного вида, то их приводят к виду «≤».
Слайд 138 Геометрическая интерпретация двойственной задачи.
Если число переменных в
прямой и двойственной задачах, образующих данную пару, равно двум, то,
используя геометрическую интерпретацию ЗЛП, можно легко найти решение данной пары задач.
Слайд 139 При этом имеет место один из следующих трех взаимно
исключающих друг друга случаев:
1.Обе задачи имеют планы
2.План имеет только одна
задача
3.Для каждой задачи двойственной пары множество планов пусто
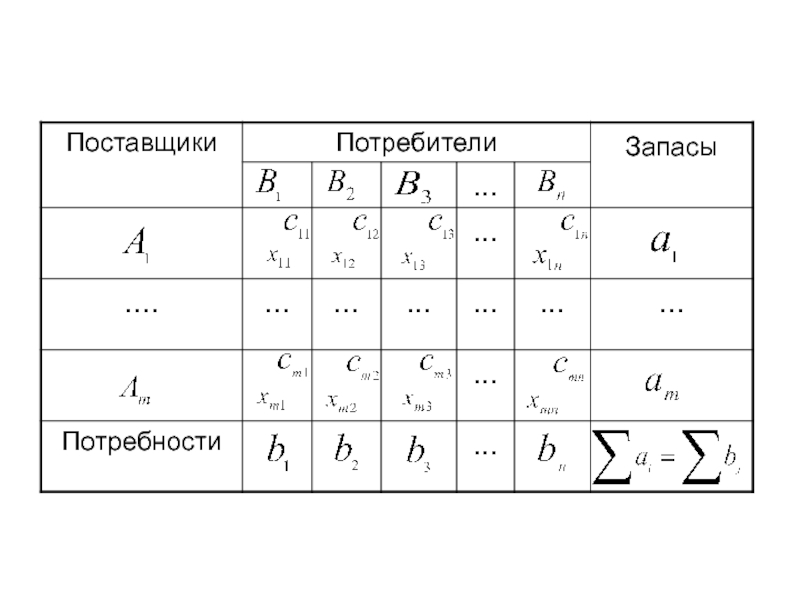
Слайд 141Пусть однородный продукт, сосредоточенный в m отправления в количествах
единиц, необходимо доставить в каждый из n пунктов назначения в количествах единиц. Стоимость перевозки единицы продукта из -го пункта отправления в -й пункт назначения равна и известна для всех комбинаций .
Слайд 142 Пусть – количество продукта, перевозимого
по маршруту . Задача заключается в
определении таких величин для всех маршрутов , при которых суммарная стоимость перевозок минимальна.
Слайд 145Математическая модель транспортной задачи сводится к минимизации целевой функции, выражающей
суммарные затраты на перевозку всего груза
Слайд 146Систему ограничений получаем из следующих условий задачи:
1. Все грузы должны
быть вывезены, т.е.
2. Все потребности должны быть удовлетворены, т.е.
Слайд 148Это есть задача ЛП с
уравнениями и
неизвестными.
В рассмотренной модели предполагается, что суммарные запасы равны суммарным потребностям
Такая модель называется закрытой
Слайд 149Теорема. Любая транспортная задача, у которой
,
имеет решение.
Слайд 150Построение первоначального опорного плана.
Слайд 151При решении задач ЛП итерационный процесс по описанию оптимального плана
начинают с определения опорного плана.
Слайд 152В общем случае система ограничений
должна содержать
линейно-
независимых уравнений, значит
невырожденный опорный план
транспортной
задачи содержит положительных
компонент или перевозок, т.е. в матрице
значений компонент положительными являются
только , а остальные равны 0
Слайд 153Клетки в таблице матрицы планирования, в которых находятся отличные от
0 перевозки, называются занятыми, остальные незанятыми. Занятые клетки соответствуют базисным
неизвестным и для невырожденного опорного плана их должно быть m+n-1.
Слайд 154Опорность плана заключается в его ацикличности (это ситуация, при которой
нельзя построить замкнутый многоугольник или цикл, все вершины которого будут
лежать в занятых клетках).
Слайд 155Циклом называется набор клеток, в котором две и только две
соседние клетки расположены в одном столбце или в одной строке
таблице, причем последняя клетка находится в той же строке или столбце, что и первая.
Слайд 156Построение циклов начинают с какой-либо занятой клетки и переходят по
столбцу (строке) к другой занятой клетке, в которой делают поворот
под прямым углом и движутся по строке (столбцу) к следующей занятой клетке и т.д., пытаясь возвратиться к первоначальной клетке.
Слайд 157Клетки, в которых происходит поворот под прямым углом, определяют вершины
цикла.
Слайд 158Если план транспортной задачи содержит более m+n-1 занятых клеток, он
не является опорным, т.к. ему соответствует линейно-зависимая система векторов.
В этом
случае в таблице всегда можно поставить замкнутый цикл, с помощью которого всегда уменьшают число занятых клеток до m+n-1.
Слайд 159Если к занятым клеткам, определяющим опорный невырожденный план, а значит
и цикличный, присоединить какую-либо незанятую клетку, то план становится не
опорным, появляется единственный цикл, все вершины которого за исключением одной, лежат в занятых клетках.
Слайд 160Метод Северо-западного угла. Метод минимальной стоимости (элемента).
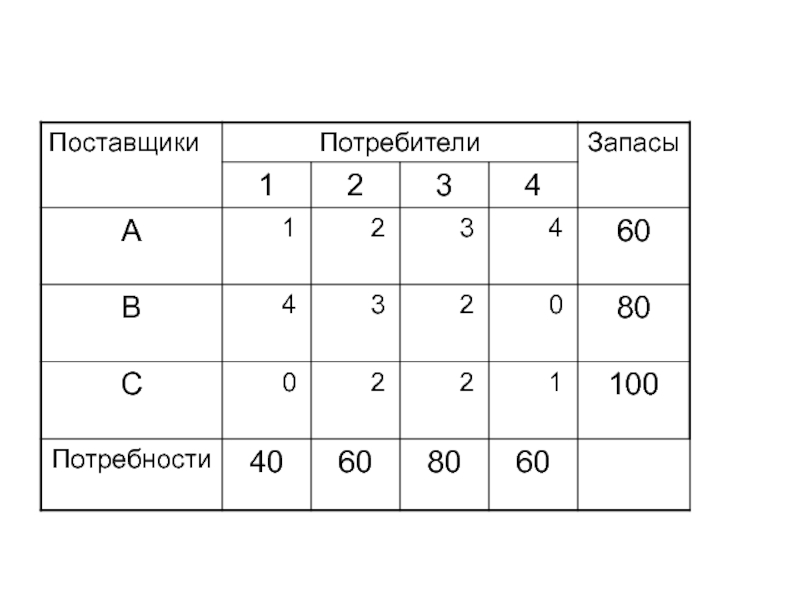
Слайд 161ПРИМЕР. В резерве трех железнодорожных станций A, B, C находятся
соответственно 60, 80, 100 вагонов. Составить оптимальный план перегона этих
вагонов к 4-ем пунктам погрузки хлеба, если пункту №1 необходимо 40 вагонов, №2 – 60, №3 – 80, №4 – 60. Стоимость перегонов одного вагона со станции A в в указанные пункты соответственно равны 1, 2, 3, 4 ден.ед., со станции B – 4, 3, 2, 0 ден.ед. и со станции C – 0, 2, 2, 1 ден.ед..
Слайд 164Общая стоимость составленного плана:
Z=40·1+20·2+40·3+40·2+40·2+60·1=
=40+40+120+80+80+60=420
Это не оптимальное решение.
Слайд 165Если при составлении опорного плана учитывать стоимость перевозки единицы груза,
то очевидно, что план будет ближе к оптимальному.
Слайд 167Суть метода минимальной стоимости (элемента) заключается в том, что из
всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ему
соответствует, помещают меньшее из чисел и .
Слайд 168Затем из рассмотренного исключают либо строку, соответствующую поставщику, запасы которого
полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены,
либо и строку и столбец. Затем из оставшейся части опять выбирают наименьшую стоимость и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.
Слайд 169Итак, опорный план трансформированной задачи построен, теперь надо из него
получит оптимальный. Можно было получить оптимальный план используя симплекс-метод, но
в нашем случае симплексная таблица будет содержать mn неизвестных, что приведет к громоздким вычислениям.
Слайд 170Поэтому для нахождения оптимального плана транспортной задачи используют другие методы,
самый распространенный из которых метод потенциалов.
Слайд 172Если решение транспортной задачи является оптимальным, то ему соответствует система
из чисел
и удовлетворяющих условиям
Слайд 173Для того чтобы план был оптимальным, необходимо выполнение следующих условий:
1)
для каждой занятой клетки сумма потенциалов должна быть равно стоимости
единицы перевозки, стоящей в этой клетке;
2) для каждой незанятой клетки сумма потенциалов должна быть меньше, либо равна стоимости единицы перевозки, стоящей в этой клетке.
Слайд 174Если хотя бы одна незанятая клетка удовлетворяет условию (2), то
опорный план не является оптимальным, и его улучшают, перемещая в
клетку некоторое количество единиц груза).
Слайд 175Проверяем условие оптимальности для незанятых клеток: если
,
то план не является оптимальным, и для каждой клетки, в которой не выполняется условие оптимальности, находим величину и записываем в левый нижний угол.
Слайд 176Выбор клетки в которую необходимо послать перевозку: транспортная задача линейного
программирования решается на min линейной функции, поэтому алгоритм ее решения
тот же, что и алгоритм симплекс-метода.
Загрузке подлежит в первую очередь клетка, которой соответствует
Слайд 177Построение цикла и определение
величины перераспределения груза:
-отмечаем знаком « +
» незанятую клетку, которую надо загрузить (знаки «-»и «+» чередуются);
-затем
находим min , где – перевозки, стоящие в вершинах цикла, отмеченных знаком « - ». Величина min определяет сколько единиц груза над перераспределить.
Слайд 178После перераспределения должно получиться m+n-1 занятых клеток.
Если для какой-либо клетки
условие оптимальности не выполняется, то можно улучшить решение двойственной задачи,
а заодно и исходной задачи, сделав эту клетку занятой и перебросив груз по циклу.
Слайд 179Для свободных клеток сумма потенциалов меньше, либо равна стоимости, следовательно
в последней таблице должно быть получено оптимальное решение исходной транспортной
задачи.
Слайд 180Открытая модель транспортной задачи.
Слайд 181Транспортная задача называется открытой если
Слайд 182Для такой задачи может быть два случая:
1) суммарные запасы превышают
суммарные
потребности, т.е.
2) суммарные потребности превышают
суммарные запасы, т.е.
Слайд 183Линейная функция остается без изменения, изменяются только ограничения:
1)
2)
Слайд 184 1) вводится фиктивный потребитель ,
потребности
которого
;
2) вводится фиктивный поставщик ,
запасы которого .
Стоимость перевозки ед.груза в этих
случаях полагают равными 0.