Методы построения сечений Комбинированный метод построения сечений

Содержание

1. Методы построения сечений Комбинированный метод построения сечений
2. Комбинированный метод построения сечений Суть
3. Пример №1. На
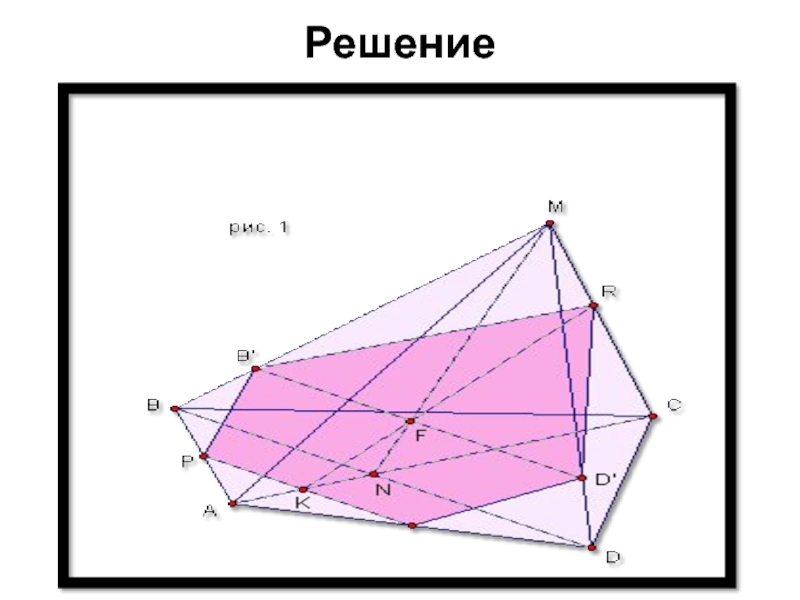
4. Решение
5. Построение сечения, проходящего через заданную
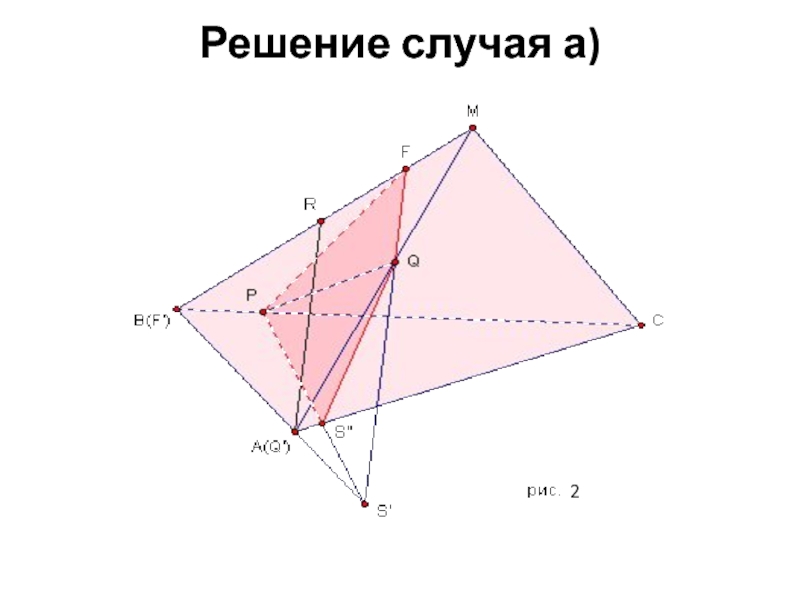
6. Решение случая а) 2
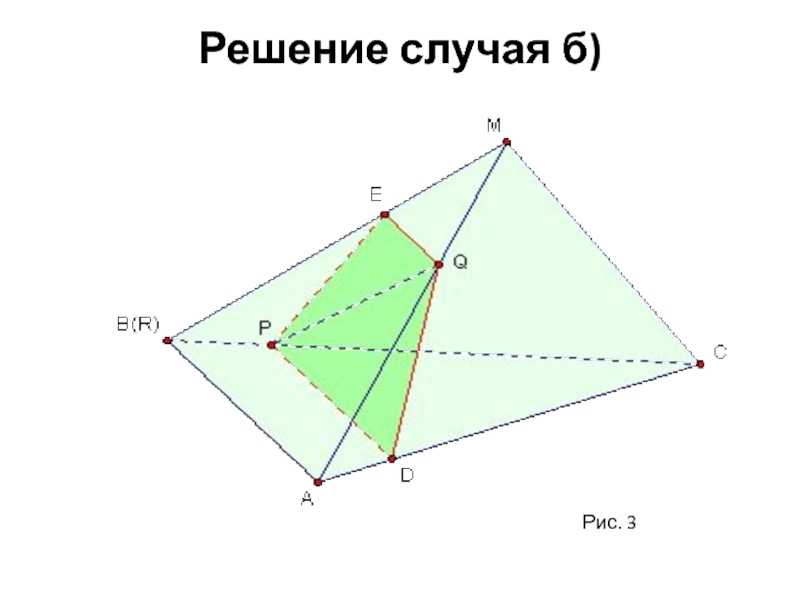
7. Решение случая б) Рис. 3
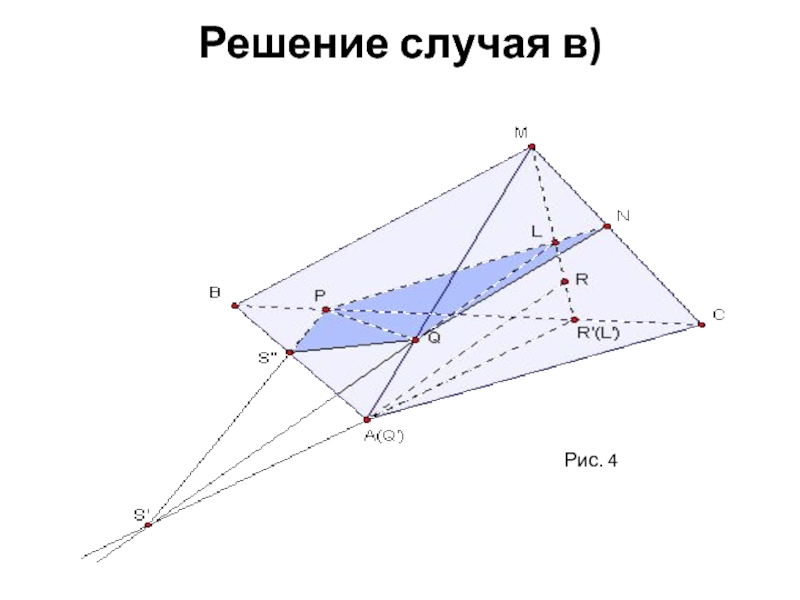
8. Решение случая в) Рис. 4
9. Пример №3. На диагоналях АС и
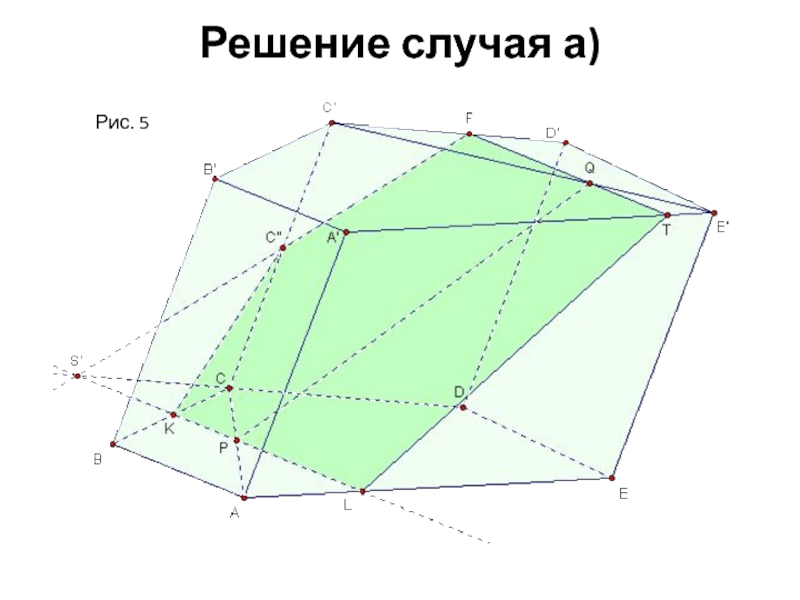
10. Решение случая а) Рис. 5
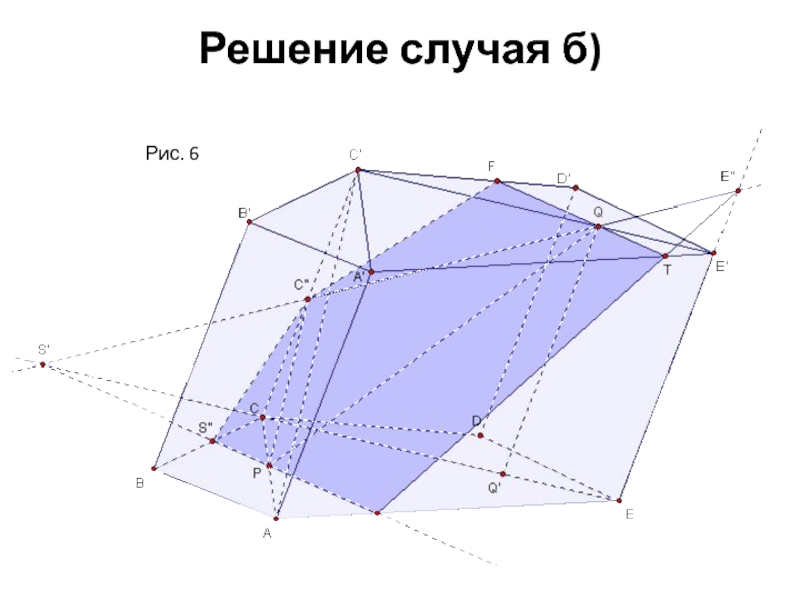
11. Решение случая б) Рис. 6
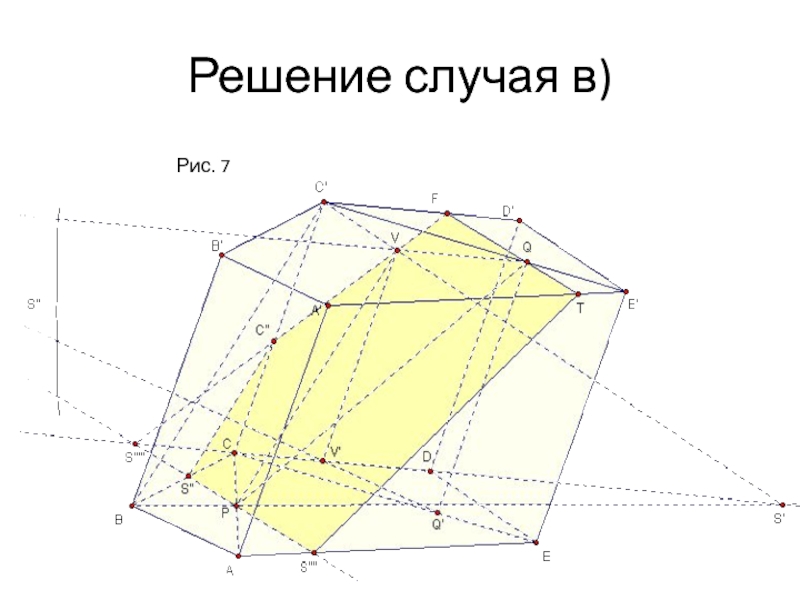
12. Решение случая в)Рис. 7
13. 2. Построение сечения, проходящего через заданную точку
14. П р и м е р 4.На
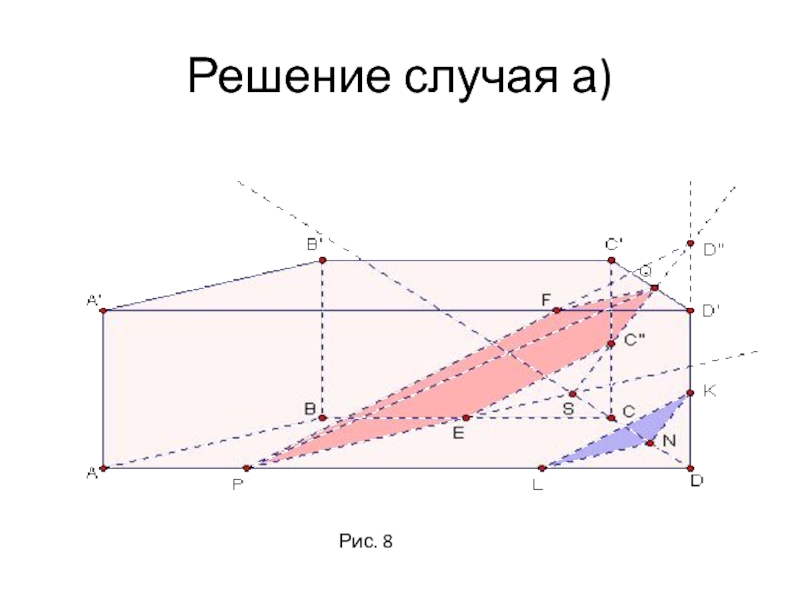
15. Решение случая а)Рис. 8
16. Решение случая б)Рис. 9
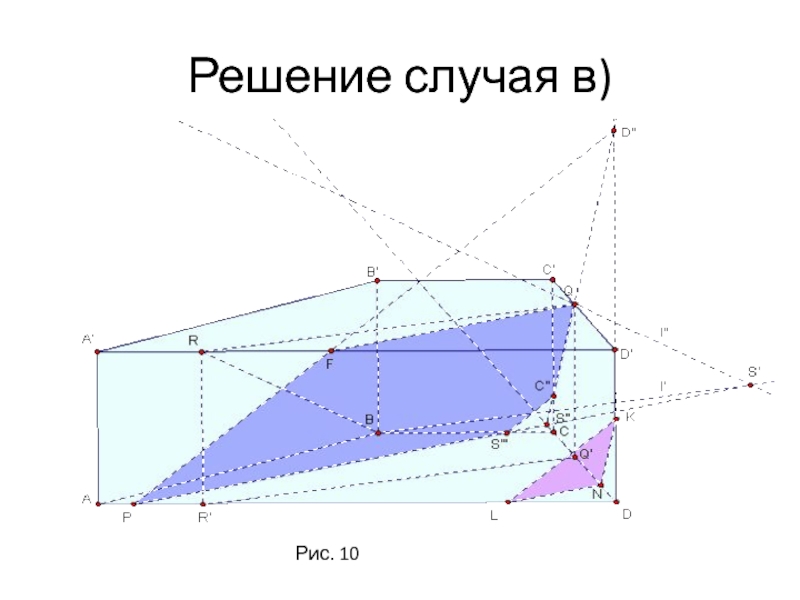
17. Решение случая в)Рис. 10
18. Пример №5На ребрах МВ и МА пирамиды
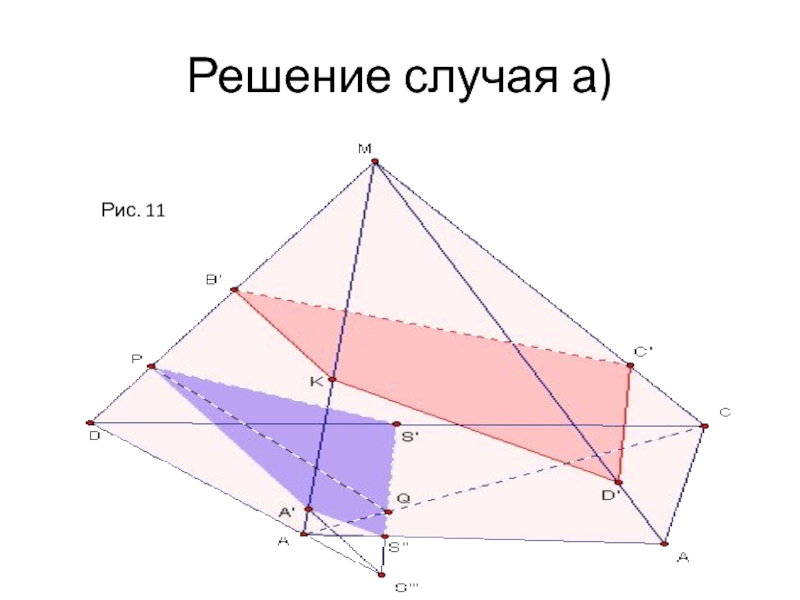
19. Решение случая а)Рис. 11
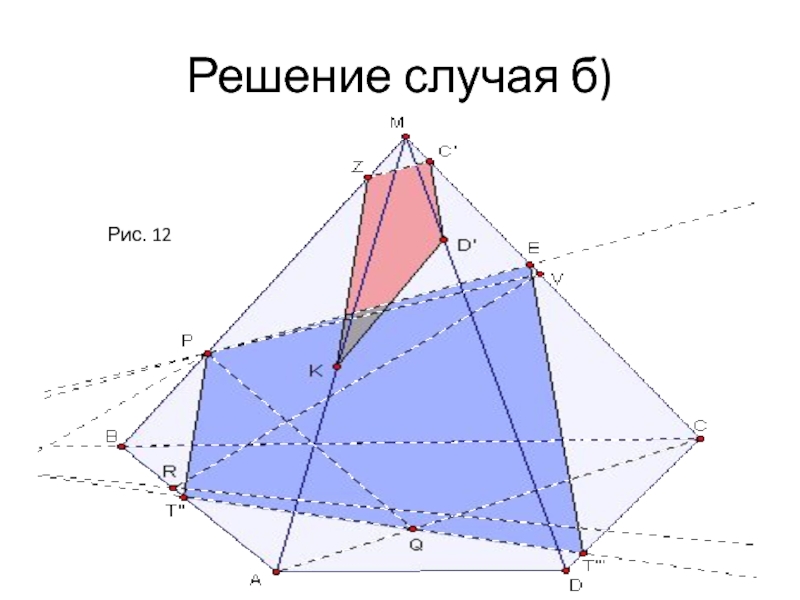
20. Решение случая б)Рис. 12
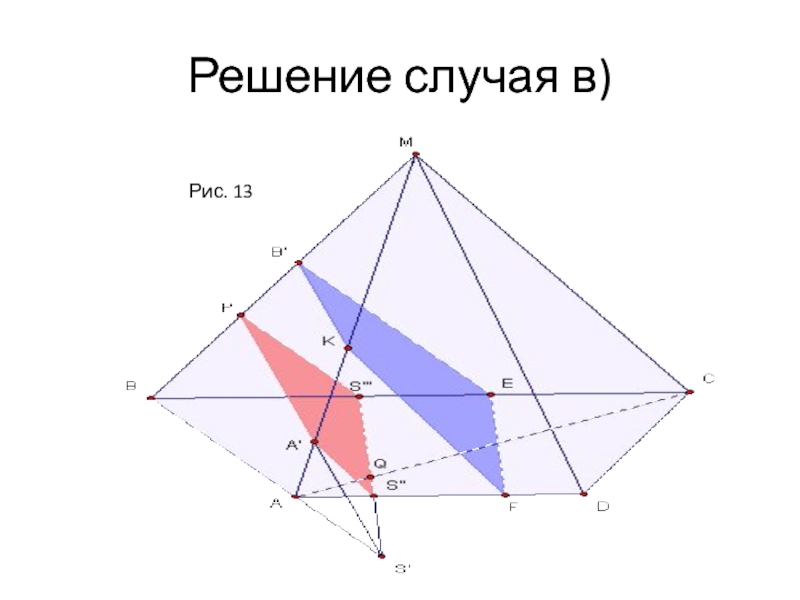
21. Решение случая в)Рис. 13
22. Скачать презентанцию

Комбинированный метод построения сечений Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом.

Главная
Разное
Методы построения сечений Комбинированный метод построения сечений

Слайды и текст этой презентации

Слайд 1Методы построения сечений Комбинированный метод построения сечений
Презентационные материалы

к практическому занятию
Методы изображений

Методы построения сечений Комбинированный метод построения сечений Презентационные материалы к практическому занятиюМетоды

Слайд 2 Комбинированный метод построения сечений
Суть комбинированного метода построения сечений многогранников состоит

в применении теорем о параллельности прямых и плоскостей в пространстве

в сочетании с аксиоматическим методом.

Комбинированный метод построения сечений Суть комбинированного метода построения сечений многогранников состоит в применении теорем о

Слайд 3 Пример №1.
На ребрах AB и AD пирамиды

MABCD зададим соответственно точки P и Q - середины этих

ребер, а на ребре MC зададим точку R. Построим сечение пирамиды плоскостью, проходящей через точки P, Q и R.

Пример №1. На ребрах AB и AD пирамиды MABCD зададим соответственно точки P

Слайд 4 Решение

Слайд 5 Построение сечения, проходящего через заданную прямую параллельную другой заданной

прямой.
Пример№2.

На ребрах BC и MA пирамиды MABC зададим соответственно точки

P и Q. Построим сечение пирамиды плоскостью @, проходящей через прямую PQ параллельно прямой AR, точку R, которую зададим следующим образом:
а) На ребре MB;
б) Она совпадает с точкой В;
в) В грани MAB.

Построение сечения, проходящего через заданную прямую параллельную другой заданной прямой. Пример№2.На ребрах BC и

Слайд 6 Решение случая а)
2

Слайд 7 Решение случая б)
Рис. 3

Слайд 8 Решение случая в)
Рис. 4

Слайд 9 Пример №3.
На диагоналях АС и C'E' оснований призмы ABCDEA'B'C'D'E' зададим

соответственно точки P и Q. Построим сечение призмы плоскостью ,

проходящей через прямую PQ параллельно одной из следующих прямых:
А) АВ;
Б) АС';
В) BC‘.

Пример №3. На диагоналях АС и C'E' оснований призмы ABCDEA'B'C'D'E' зададим соответственно точки P и Q.

Слайд 10 Решение случая а)
Рис. 5

Слайд 11Решение случая б)
Рис. 6

Слайд 12Решение случая в)
Рис. 7

Слайд 132. Построение сечения, проходящего через заданную точку параллельно двум заданным

скрещивающимся прямым.
Пусть требуется построить сечение многогранника плоскостью, проходящей через заданную

точку К параллельно двум заданным скрещивающимся прямым l и m. При решении задач этого вида можно применять следующий план построения:

1.Выберем некоторую точку W. (Эта точка может лежать на одной из заданных скрещивающихся прямых, может совпадать с точкой К.)
2.Через точку W проведем прямые l' и m'. (Естественно, если точка W лежит на одной из прямых, например на прямой l, то прямая l' совпадает с прямой l.)
3. Пересекающимися прямыми l' и m' определяется плоскость бетта - плоскость вспомогательного сечения многогранника. Строим сечение многогранника плоскостью бетта.
4. Построим сечения многогранника плоскостью альфа, проходящей через точку K, параллельно плоскости бетта.

2. Построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым. Пусть требуется построить сечение многогранника

Слайд 14П р и м е р 4.
На ребрах AD и

С'D' призмы ABCDA'В'С'D', зададим соответственно точки P и Q, а

на ребре DD' зададим точку К. Построим сечение призмы плоскостью альфа, проходящей через точку К параллельно прямой PQ и одной из следующих прямых:
а) АВ;
б) А'В;
в) BR, точку R которой зададим на ребре A'D'.

П р и м е р 4.На ребрах AD и С'D' призмы ABCDA'В'С'D', зададим соответственно точки P

Слайд 15Решение случая а)
Рис. 8

Слайд 16Решение случая б)
Рис. 9

Слайд 17Решение случая в)
Рис. 10

Слайд 18Пример №5
На ребрах МВ и МА пирамиды МАВСD зададим соответственно

точки Р и К, и на отрезке АС зададим точку

Q. Построим сечение пирамиды плоскостью альфа, проходящей через точку К параллельно прямой PQ и одной из следующих прямых:
а) CD;
б) МС;
в) RV, точки R и V которой зададим соответственно на ребрах АВ и МС пирамиды.