Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Механика грунтов
Содержание
- 1. Механика грунтов
- 2. Основная литератураЦытович Н.А. Механика грунтов. – М.:
- 3. Дополнительная литератураБерлинов М.В. Основания и фундаменты. –
- 4. Справочно-нормативные учебно-методические материалы СТ РК 25100-2002
- 5. Структура дисциплины «Геотехника II»
- 6. Механика грунтовГрунт – это горная порода, находящаяся в сфере воздействия инженерной деятельности человека.
- 7. Схема электромолекулярного взаимодействия в системе твердая частица
- 8. Формы воды в грунтах1 – абсолютно сухой
- 9. Состав грунтов Грунт = твердые частицы +
- 10. Схема электромолекулярного взаимодействия в системе твердая частица
- 11. Физические свойства грунтовПесчаныхГранулометрический составПлотность, ρ г/см³Влажность W
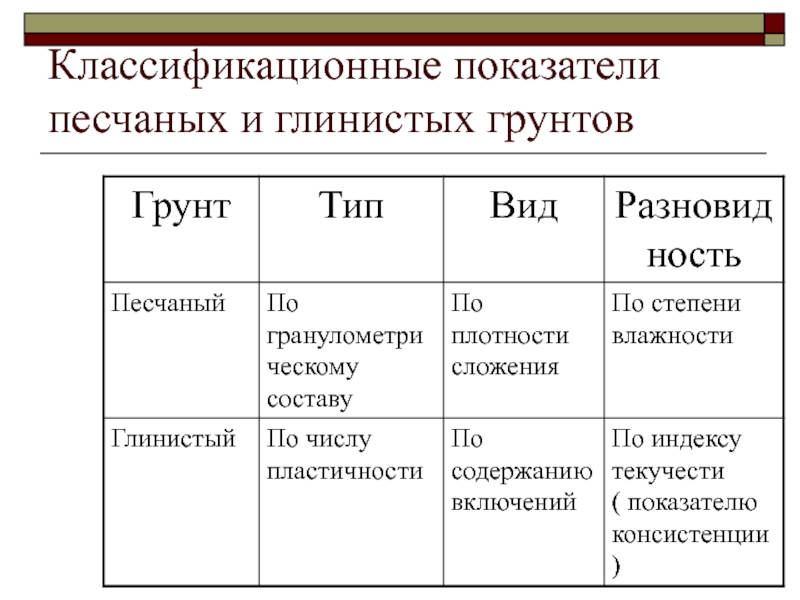
- 12. Классификационные показатели песчаных и глинистых грунтов
- 13. Классификационные характеристики глинистых грунтовЧисло пластичности: Ip=WL-WpПоказатель консистенции: IL=(W-Wp)/(WL-Wp)
- 14. Оценка плотности сложения песков Динамическое зондирование
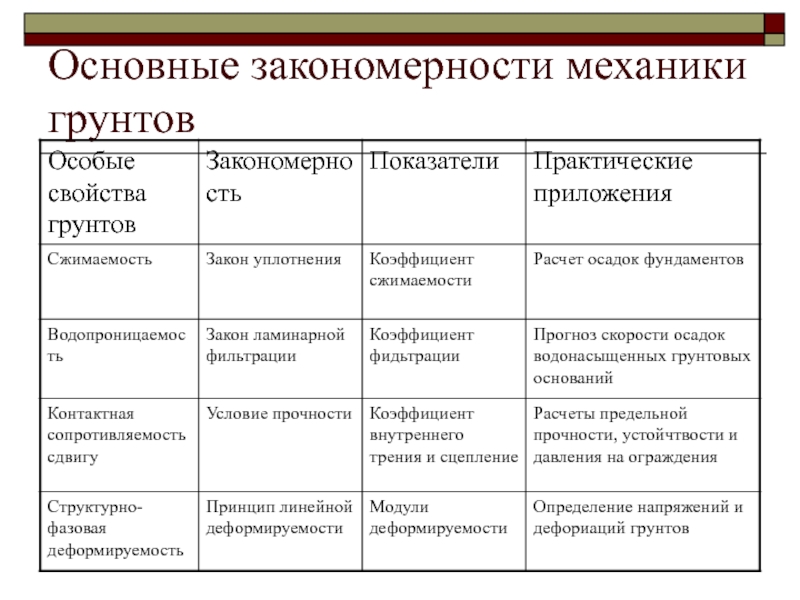
- 15. Основные закономерности механики грунтовСжимаемость – обусловлена изменением
- 16. Основные закономерности механики грунтов
- 17. Сжимаемость грунтовРазличают: - уплотняемость (при кратковременном действии
- 18. Компрессионная зависимостьХарактеризует: - коэффициент сжимаемости грунтов mо=tgα - коэффициент относительной сжимаемости mυ=mo/(1+eo)
- 19. Закон уплотнения (сформулировал Н.А.Цытович, 1934г.)Бесконечно малое изменение
- 20. Общий случай компрессионной зависимостиХарактеризуется:- σx=σy- σz=p-
- 21. Коэффициент бокового давленияКоэффициент бокового давления (ξ) –
- 22. Давление в грунтахPz – эффективные - давления
- 23. Давление в грунтахВ любой момент времени в
- 24. Схемы, поясняющие две системы давлений в водонасыщенных
- 25. Сопротивление грунтов сдвигуСпособность грунта сопротивляться внешним нагрузкам
- 26. Схемы испытаний грунтов на сдвигА) при постоянно
- 27. Закон Кулона, 1773г.Предельное сопротивление сыпучих грунтов сдвигу
- 28. Общий вид сдвигового прибора с кинематической схемой проведения испытаний
- 29. Схема сдвигового прибора (Италия)
- 30. Сопротивление сдвигу связных грунтовВ связных грунтах частицы
- 31. Испытание грунтов на трехосное сжатиеОтражают наиболее реальную работу грунта основанияСхема стабилометра: σ1=P; σ2=σ3;
- 32. Приборы трехосного сжатия (стабилометры)
- 33. Методика проведения испытаний в трехосных приборахВ процессе
- 34. Случаи предельных напряжений при сдвиге (теория прочности
- 35. Прочность грунтовВ настоящее время наиболее оправданной для
- 36. Основные критерии прочностиКритерий прочности Кулона-мора ( для
- 37. Прибор трехосного сжатия1- нагружающее устройство при принудительно
- 38. Структурно-фазовая деформируемость грунтовПри действии внешней нагрузки отдельные
- 39. Определение напряжений в грунтовой толщеВ механике грунтов
- 40. Доказательство применимости теории упругости к грунтам (постулаты теории упругости).
- 41. Случай пространственных задачДействие сосредоточенной силы ( задача
- 42. Определение напряжений в точке грунтового массиваВ случае
- 43. Определение напряжений в точке грунтового массива
- 44. Действие местной равномерно распределенной нагрузкиДля площадок под
- 45. Влияние площади загруженияЧем больше площадь загружения, тем медленнее загасают с глубиной напряжения от внешнего давления.
- 46. Распределение напряжений в случае плоской задачиПрименяется для
- 47. Эпюры распределения сжимающих напряжений σz в массиве
- 48. Линии равных напряжений в линейно деформируемом массиве
- 49. Эллипсы напряжений при действии равномерно распределенной нагрузки в условиях плоской задачи
- 50. Произвольный вид нагрузкиа – разбивка криволинейной эпюры
- 51. Контактная задачаКонтактным называют давление по подошве фундаментаДля
- 52. Распределение напряжений на подошве фундамента (Контактная
- 53. Теоретические исследования по этому вопросу провел Буссинеcко
- 54. Напряжение по подошве штампа
- 55. Напряжения от собственного веса грунта
- 56. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Казахская головная архитектурно-строительная академия
Факультет общего строительства Дисциплина
«Геотехника II»
Доктор технических
наук
Слайд 2Основная литература
Цытович Н.А. Механика грунтов. – М.: Издательство АСВ, 1983.
– 288 с.
Далматов Б.И., Бронин В.Н., Карлов В.Д. и др.
Механика грунтов. Ч.1. Основы геотехники в строительстве. – М.: АСВ, 2000. – 204 c.Далматов Б.И., Бронин В.Н., Карлов В.Д. и др. Основания и фундаменты. Ч.2. Основы геотехники. – М.: АСВ, 2002. – 392 c.
Ухов С.Б., Семёнов В.В., Знаменский В.В. и др. Механика грунтов, основания и фундаменты. – М.: Высшая школа, 2002. – 566 с.
Слайд 3Дополнительная литература
Берлинов М.В. Основания и фундаменты. – М.: Высшая школа,1999.
– 319 с.
Далматов Б.И., Бронин В.Н., Голли А.В. и др.
Проектирование фундаментов зданий и подземных сооружений. – М.: АСВ, 2001. – 440 c.Веселов В.А. Проектирование оснований и фундаментов. – М.: Стройиздат, 1990. – 415 с.
Шутенко Л.Н., Гильман А.Д., Лупан Ю.Т. Основания и фундаменты. – Киев: Высшая школа, 1989. – 328 с.
Основания, фундаменты и подземные сооружения. Справочник проектировщика./Под ред. Е.А.Сорочана, Ю.Г.Трофименкова. - М.: Стройиздат, 1985. – 480 с.
Берлинов М.В.,Ягупов Б.А. Примеры расчета оснований и фундаментов. М.: Стройиздат, 1986. – 173 с.
Слайд 4Справочно-нормативные учебно-методические материалы
СТ РК 25100-2002 Грунты. Классификация. 2002г.
СНиП
РК 5.01-01-2002 Основания зданий и сооружений . – Астана, 2002.
– 83 с.СНиП РК 1.02-18-2004 Инженерные изыскания для строительства. 2004 г.
СН РК 1.02-18-2007. Инженерно-геологические изыскания для строительства. Технические требования к производству работ. Астана. 2008г.
МСП 5.01-102-2002 Проектирование и устройство оснований зданий и сооружений. Астана, 2005- 106 с.
СНиП 2.01.15-88. Инженерная защита территорий, зданий и сооружений от опасных геологических процессов. Основные положения проектирования. М.: Стройиздат, 1989
СНиП 5.01.03-2002. Свайные фундаменты. Астана, 2002.
СНиП РК 2.03-30-2006 Строительство в сейсмических районах.
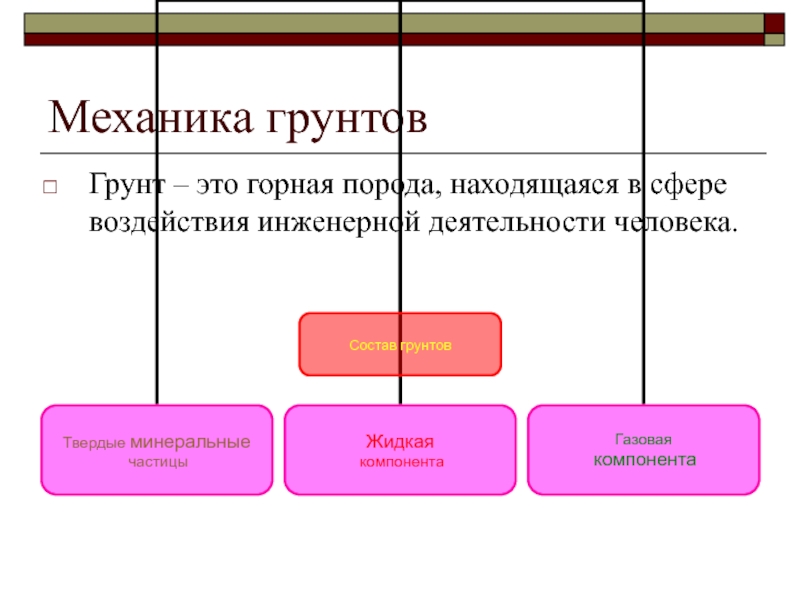
Слайд 6Механика грунтов
Грунт – это горная порода, находящаяся в сфере воздействия
инженерной деятельности человека.
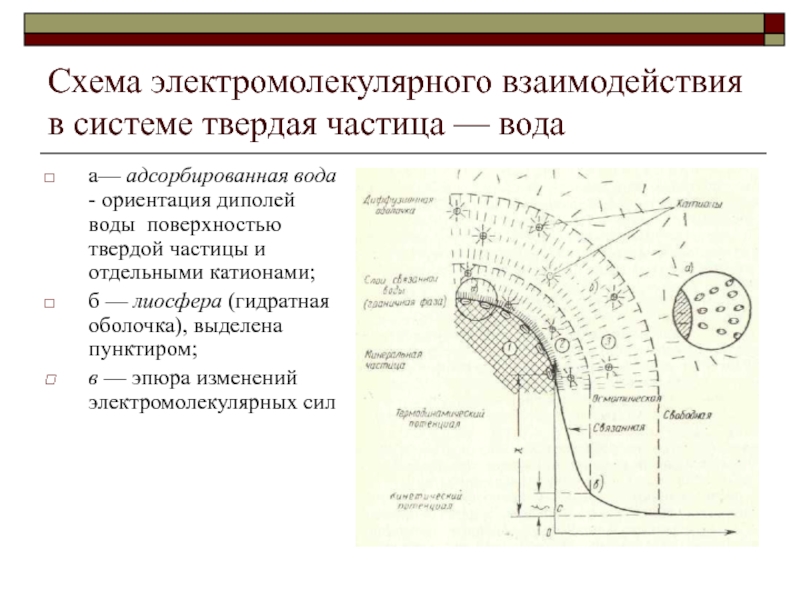
Слайд 7Схема электромолекулярного взаимодействия в системе твердая частица — вода
а— адсорбированная
вода - ориентация диполей воды поверхностью твердой частицы и отдельными
катионами;б — лиосфера (гидратная оболочка), выделена пунктиром;
в — эпюра изменений электромолекулярных сил
Слайд 8Формы воды в грунтах
1 – абсолютно сухой грунт
2 – воздушно-сухой
грунт
3 – грунт, насыщенный гигроскопической (прочносвязанной водой)
4 - грунт в
состоянии максимального насыщения молекулярно связанной водой5 – грунт, содержащий гравитационную воду
Слайд 9Состав грунтов
Грунт = твердые частицы + вода + газ
Свойства
твердых частиц.
Свойства твердых (минеральных) частиц зависят от размеров.
Классификация твердых частиц:
Классификация
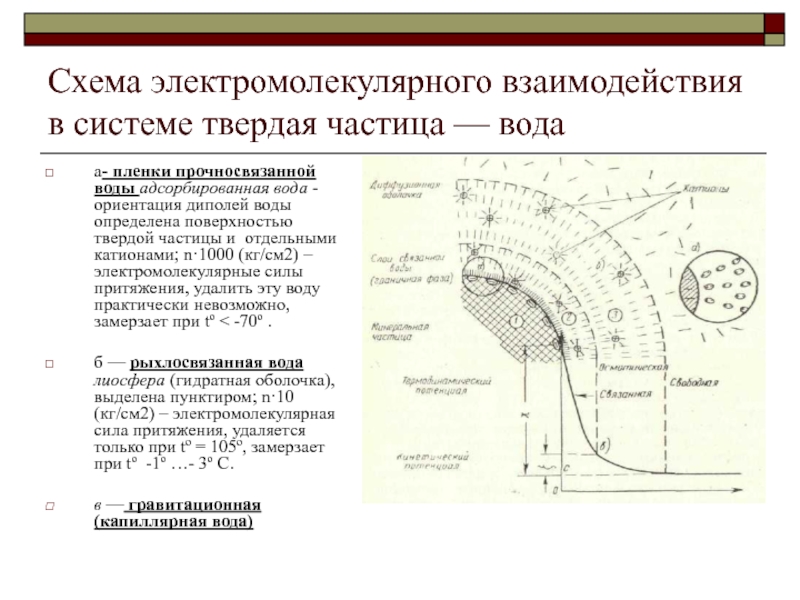
грунтов (простейшая) Слайд 10Схема электромолекулярного взаимодействия в системе твердая частица — вода
а- пленки
прочносвязанной воды адсорбированная вода - ориентация диполей воды определена поверхностью
твердой частицы и отдельными катионами; n·1000 (кг/см2) – электромолекулярные силы притяжения, удалить эту воду практически невозможно, замерзает при tº -70º .б — рыхлосвязанная вода лиосфера (гидратная оболочка), выделена пунктиром; n·10 (кг/см2) – электромолекулярная сила притяжения, удаляется только при tº = 105º, замерзает при tº -1º …- 3º C.
в — гравитационная (капиллярная вода)
Слайд 11Физические свойства грунтов
Песчаных
Гранулометрический состав
Плотность, ρ г/см³
Влажность W %
Плотность сухого грунта,
ρ г/см³
Пористость, п
Коэффициент пористости, е
Степень влажности, Sr
Глинистых
Плотность, ρ г/см³
Влажность, W
%Влажность на границе раскатывания, Wp %
Влажность на границе текучести, WL %
Плотность сухого грунта, ρ г/см³
Пористость, п
Коэффициент пористости, е
Степень влажности, Sr
Число пластичности, Ip
Показатель консистенции, IL
Слайд 13Классификационные характеристики глинистых грунтов
Число пластичности: Ip=WL-Wp
Показатель консистенции: IL=(W-Wp)/(WL-Wp)
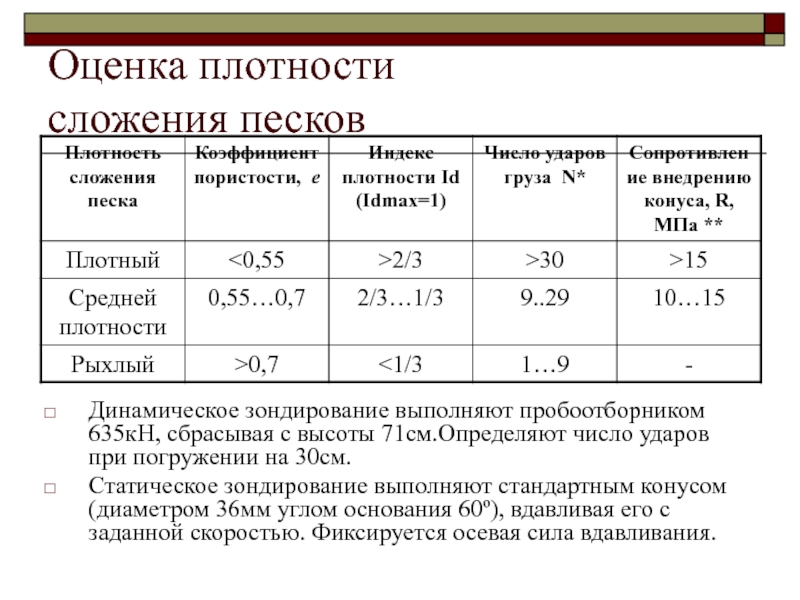
Слайд 14Оценка плотности
сложения песков
Динамическое зондирование выполняют пробоотборником 635кН, сбрасывая
с высоты 71см.Определяют число ударов при погружении на 30см.
Статическое зондирование
выполняют стандартным конусом (диаметром 36мм углом основания 60º), вдавливая его с заданной скоростью. Фиксируется осевая сила вдавливания.Слайд 15Основные закономерности механики грунтов
Сжимаемость – обусловлена изменением пористости, а следовательно
и объема. Происходит переупаковка частиц
Контактная сопротивляемость сдвигу – обусловлена лишь
внутренним трением в сыпучих грунтах и трением со сцеплением в связных.Водопроницаемость – свойство пористых тел, является для грунтов переменной величиной, изменяющейся в процессе уплотнения под нагрузкой.
Деформируемость – зависит от податливости и сопротивляемости структурных связей грунтов, отдеформируемости отдельных компонентов образующих грунты.
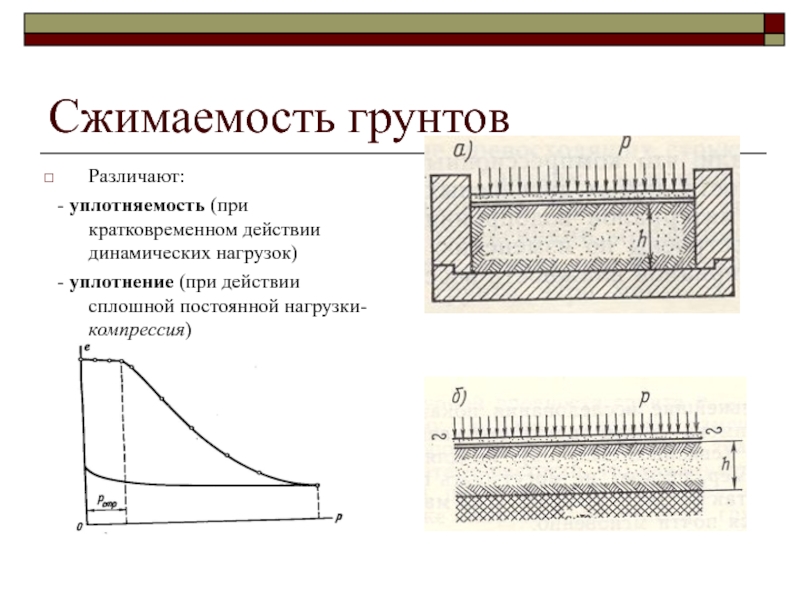
Слайд 17Сжимаемость грунтов
Различают:
- уплотняемость (при кратковременном действии динамических нагрузок)
-
уплотнение (при действии сплошной постоянной нагрузки- компрессия)
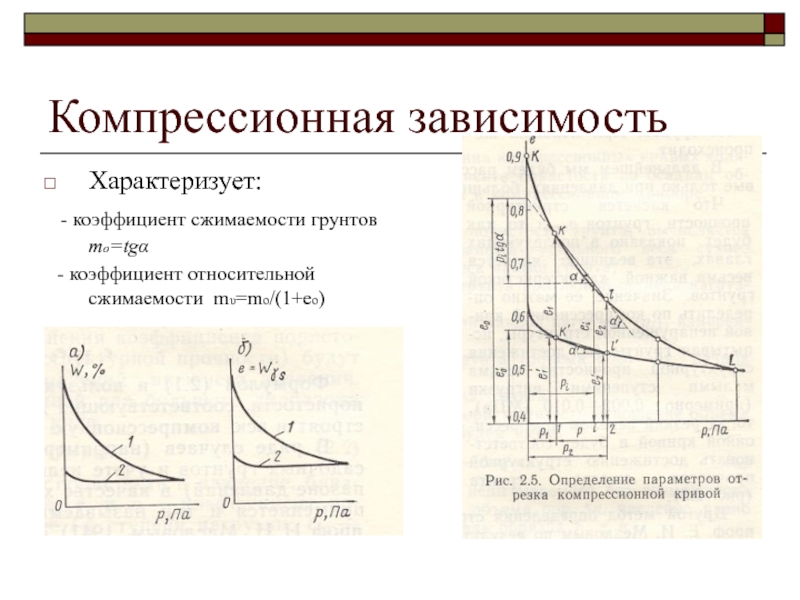
Слайд 18Компрессионная зависимость
Характеризует:
- коэффициент сжимаемости грунтов mо=tgα
- коэффициент относительной
сжимаемости mυ=mo/(1+eo)
Слайд 19Закон уплотнения
(сформулировал Н.А.Цытович, 1934г.)
Бесконечно малое изменение относительного объема пор грунта
прямо пропорционально бесконечно малому изменению давления:
de=-modP
Слайд 20Общий случай
компрессионной зависимости
Характеризуется:
- σx=σy
- σz=p
- εx=0
Θ=σx+σy+σz=p(1+2ξο)
Изменение коэффициента пористости (или
влажности)грунтовой массы в данной точке может произойти лишь при суммы
главных напряжений в этой же точке.Слайд 21Коэффициент бокового давления
Коэффициент бокового давления (ξ) – есть отношение приращения
горизонтального давления грунта dq к приращению действующего вертикального давления
ξ=dq/dp
Для
песчаных грунтов: ξ=0,25-0,37;Для глинистых грунтов: ξ=0,11-0,82;
Слайд 22Давление в грунтах
Pz – эффективные - давления в скелете грунта,
уплотняют и упрочняют грунт, передаются только через точки и площадки
контактов твердых частиц.Pw – нейтральные – не уплотняют и не упрочняют грунт, а создают лишь напор в воде, вызывающий ее фильтрацию.
В полностью водонасыщенной грунтовой массе имеет место соотношение P=Pz+Pw или σ=ē+u;
Эффективное давление ē в любой точке водонасыщенного грунта равно разности между полным σ и нейтральным u напряжениями
Слайд 23Давление в грунтах
В любой момент времени в полностью водонасыщенной грунтовой
массе имеет место соотношение: Р = Рz + Рw
, где Р – полное давлениеПри t = 0 Р = Рw
При t = t1 Р = Рw+ Рz
При t = Р = Рz – это теоретически, практически для того чтобы Рw=0, требуется длительный период времени. времени в полностью
Осадка может происходить и при Р = Рz за счет явлений ползучести скелета.
Слайд 24Схемы, поясняющие две системы давлений в водонасыщенных грунтах
а) Схема передачи
давления на скелет грунта
б) Модель сжатия грунтовой массы
( нагрузка
вначале вся передается на воду, затем по мере сжатия на скелет грунта) Слайд 25Сопротивление грунтов сдвигу
Способность грунта сопротивляться внешним нагрузкам определяется внутренним сопротивлением
сдвигу частиц за счет сил трения на их контактах и
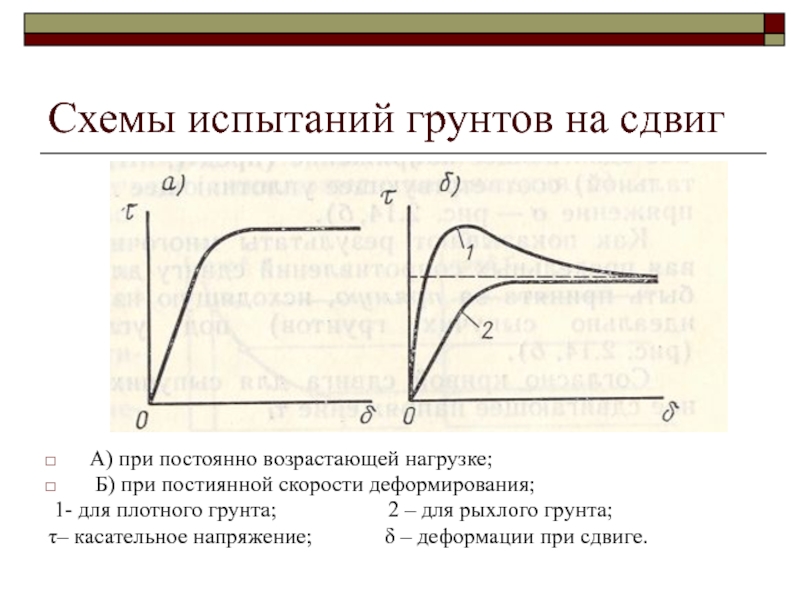
силами сцепления, под которым понимают сопротивление структурных связей всякому перемещению связываемых ими частиц.Слайд 26Схемы испытаний грунтов на сдвиг
А) при постоянно возрастающей нагрузке;
Б) при постиянной скорости деформирования;
1- для плотного грунта;
2 – для рыхлого грунта;τ– касательное напряжение; δ – деформации при сдвиге.
Слайд 27Закон Кулона, 1773г.
Предельное сопротивление сыпучих грунтов сдвигу есть сопротивление трению,
прямо пропорциональное нормальному давлению
предτi=tgφ*σi ;
где: φ – угол внутреннего
трения грунта.Слайд 30Сопротивление сдвигу связных грунтов
В связных грунтах частицы и агрегаты частиц
связанны пластичными водно-колоидными и частично жесткими, цементационно-кристализационными связями, поэтому сопротивление
сдвигу будет в высокой степени зависеть от связности, т.е. сил сцепления.предτi=tgφ*σi + с ;
где: φ – угол внутреннего трения грунта;
с – удельное сцепление.
Выделяют три режима испытаний грунтов:
1 – консолидированно-дренированное;
2 – неконсолидированно-недренированное;
3 – консолидированно-недренированное
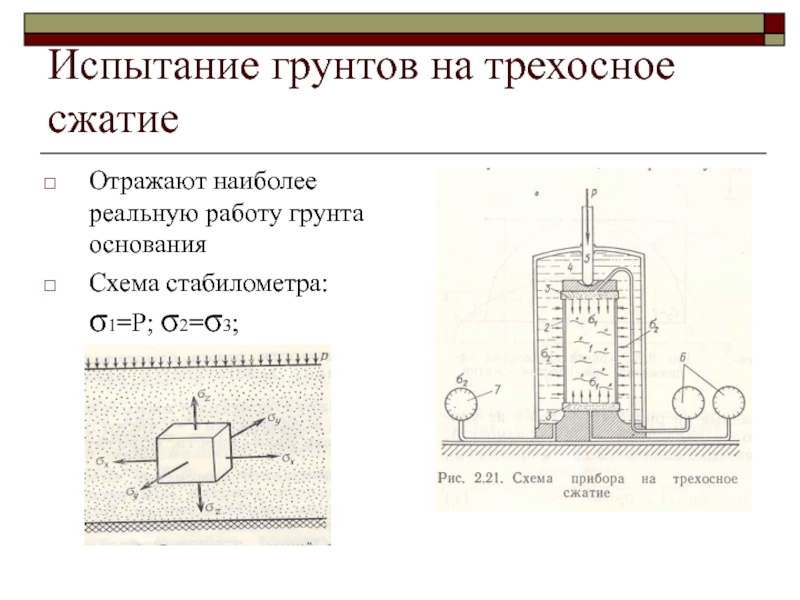
Слайд 31Испытание грунтов на трехосное сжатие
Отражают наиболее реальную работу грунта основания
Схема
стабилометра: σ1=P; σ2=σ3;
Слайд 33Методика проведения испытаний в трехосных приборах
В процессе испытаний оставляем неизменным
Р2 и увеличиваем Р1. Максимальное значение Р1 будет тогда, когда
круг коснется прямой Кулона τпр = Р tg φ - уравнение, описывающие предельное сопротивление грунта сдвигу для песчаного грунта, т.е. процесс разрушения.Слайд 34Случаи предельных напряжений при сдвиге (теория прочности Мора)
Условие предельного равновесия
сыпучих грунтов
sinφ=(σ1-σ2)/(σ2+σ1) ;
Условие предельного равновесия связных грунтов
sinφ=(σ1-σ2)/(σ2+σ1+2сtgφ) ;
Слайд 35Прочность грунтов
В настоящее время наиболее оправданной для грунтовых материалов является
концепция, по которой разрушение грунта происходит по определенным площадкам скольжения.
Эта концепция в развернутом виде состоит из 3-х положений:Разрушение происходит по площадкам скольжения, определяемым в пространстве главных напряжений σ1>σ2>σ3 нормалью ν с направляющими косинусами {l,m,n};
Положение площадки определяется определяется некоторыми дополнительными условиями;
На площадке с нормалью ν разрушение происходит по закону сухого трения Кулона, т.е. |τν|= сν - tgφ*σν;
Слайд 36Основные критерии прочности
Критерий прочности Кулона-мора ( для решения плоских задач);
Критерий
прочности Хилла- Треска (для решения плоских задач);
Критерий прочности Мизеса-Шлейхера-Боткина (для
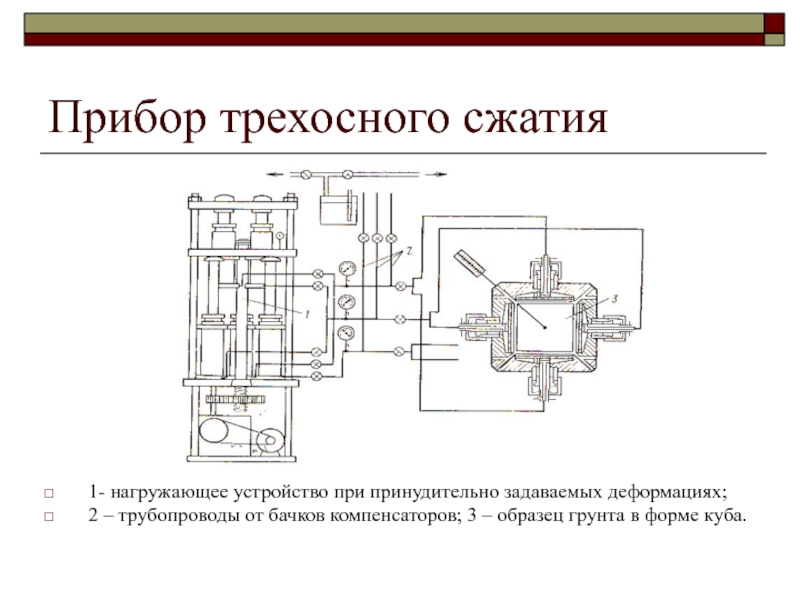
решения пространственных задач)Слайд 37Прибор трехосного сжатия
1- нагружающее устройство при принудительно задаваемых деформациях;
2 –
трубопроводы от бачков компенсаторов; 3 – образец грунта в форме
куба.Слайд 38Структурно-фазовая деформируемость грунтов
При действии внешней нагрузки отдельные фазы грунтов (компоненты)
по разному сопротивляются силовым воздействиям и по разному деформируются.
Общий вид:
ε=αс*σс+αn*(σn-σс)
m;αс=l/E; αn=β/Еro(z
E – модуль упругости (Юнга),
Еro(z) – модуль общей линейной деформации
Слайд 39Определение напряжений в грунтовой толще
В механике грунтов для изучения напряженного
состояния грунтов применяют аппарат теории упругости.
При решении вопроса о распределении
напряжений в грунтовой толще используют теорию линейно-деформируемых тел.При определении общих деформаций грунтов учитывают добавочные условия, вытекающие из физической природы грунтов, их сжимаемость, ползучесть и т.п.
Дополнительным условием будет также отсутствие перераспределений фаз грунта в рассматриваемом объеме во времени.
Слайд 41Случай пространственных задач
Действие сосредоточенной силы ( задача Ж.Буссинеско)
Требуется определить:
Составляющие напряжения
σz σy σx τxy τzy τzx
Получаемое решение:
σz=3pz3/2πR5τzy=3pyz2/2πR5
τzx=3pxz2/2πR5
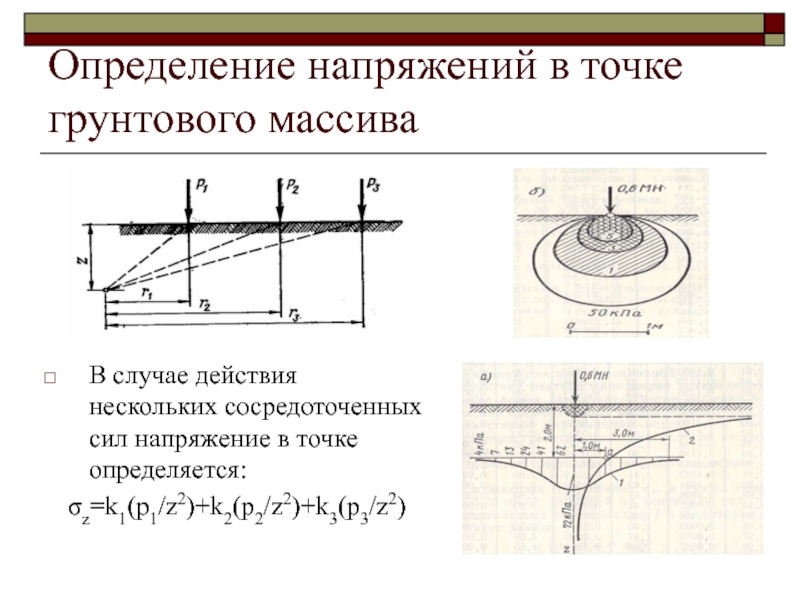
Слайд 42Определение напряжений в точке грунтового массива
В случае действия нескольких сосредоточенных
сил напряжение в точке определяется:
σz=k1(p1/z2)+k2(p2/z2)+k3(p3/z2)
Слайд 44Действие местной равномерно распределенной нагрузки
Для площадок под центром загруженного прямоугольника
максимальное сжимающее напряжение равно: maxσzo=kop;
Для площадок под углом загруженного прямоугольникасжимающее
напряжение равно: σzс=kсp;Где: ko , kс –коэффициенты, определояемые по таблице СНиП 2.02.01-83; р – интенсивность нагрузки.
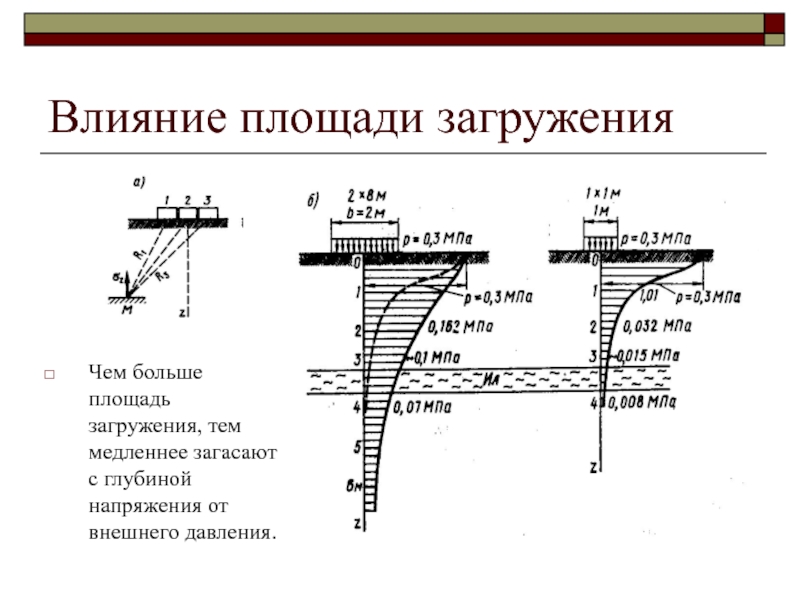
Слайд 45Влияние площади загружения
Чем больше площадь загружения, тем медленнее загасают с
глубиной напряжения от внешнего давления.
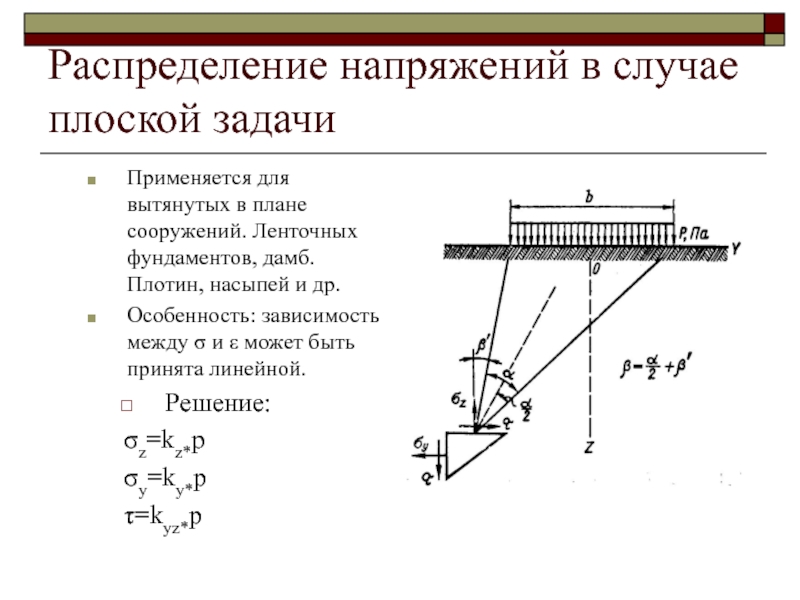
Слайд 46Распределение напряжений в случае плоской задачи
Применяется для вытянутых в плане
сооружений. Ленточных фундаментов, дамб. Плотин, насыпей и др.
Особенность: зависимость между
σ и ε может быть принята линейной.Решение:
σz=kz*p
σy=ky*p
τ=kyz*p
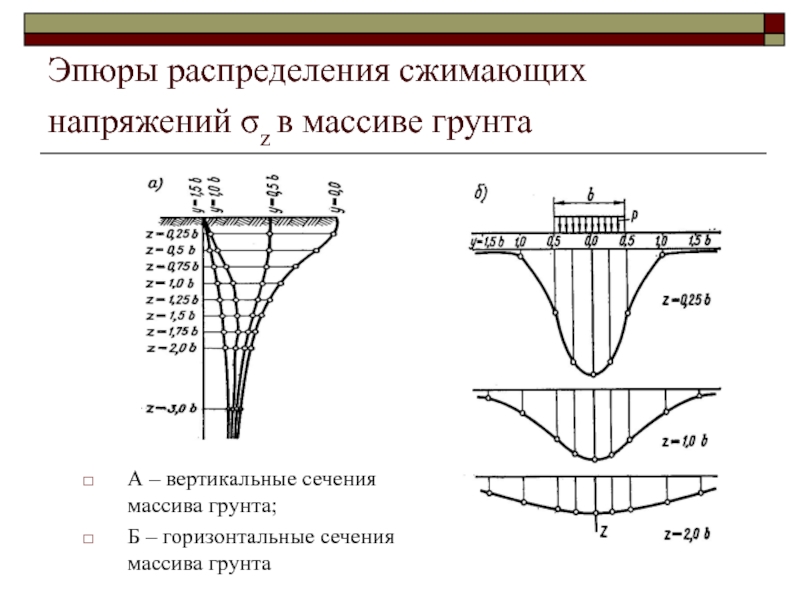
Слайд 47Эпюры распределения сжимающих напряжений σz в массиве грунта
А –
вертикальные сечения массива грунта;
Б – горизонтальные сечения массива грунта
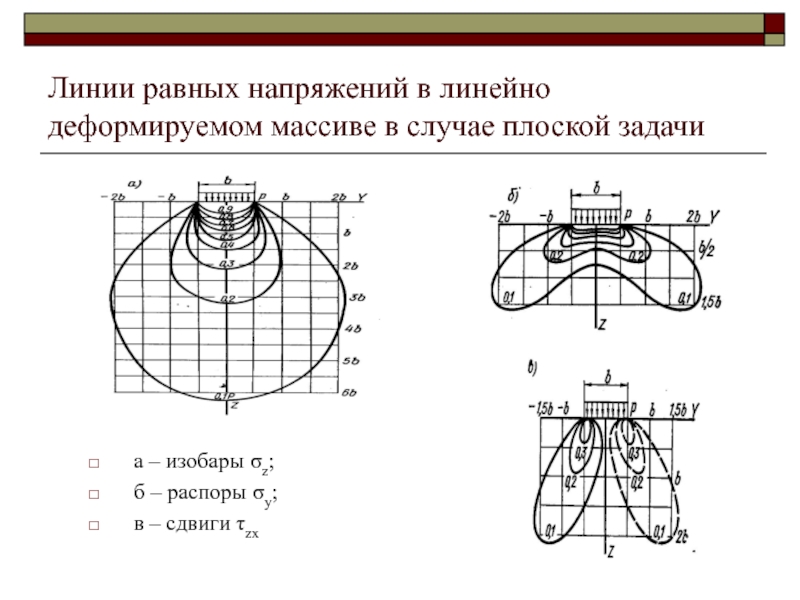
Слайд 48Линии равных напряжений в линейно деформируемом массиве в случае плоской
задачи
а – изобары σz;
б – распоры σy;
в – сдвиги
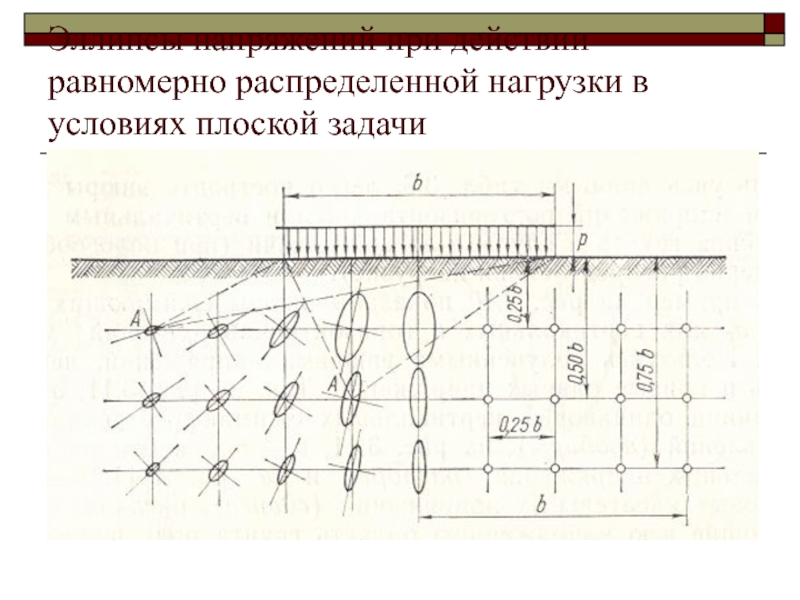
τzxСлайд 49Эллипсы напряжений при действии равномерно распределенной нагрузки в условиях плоской
задачи
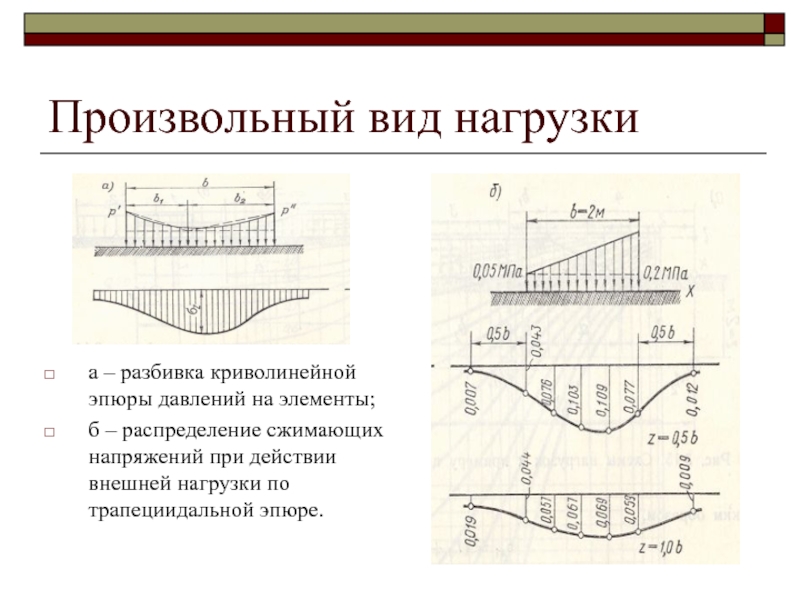
Слайд 50Произвольный вид нагрузки
а – разбивка криволинейной эпюры давлений на элементы;
б
– распределение сжимающих напряжений при действии внешней нагрузки по трапециидальной
эпюре.Слайд 51Контактная задача
Контактным называют давление по подошве фундамента
Для определения контактного напряжения
совместно решается два уравнения:
Дифференциальное уравнение изогнутой оси балки;
Физическое уравнение связей
между действующим давлением и осадкой.EбJб(d4s/dx4)=qxpx;
где: EбJб-жесткость балки
S – прогиб балки
Слайд 52Распределение напряжений на подошве фундамента
(Контактная задача)
Этот вопрос имеет
особое значение для гибких фундаментов, рассчитываемых на изгиб.
Если известно Рконт,
то загружая этой величиной фундамент, можно легко определять усилия в конструкции тела фундамента.Из курса сопротивления материалов известно, что напряжения для сжатых конструкций при прямолинейной эпюре определяются по обобщенной формуле:
max, min =(N/F) +-(M/W) - но здесь не учитывается работа сжимаемого основания.
Слайд 53Теоретические исследования по этому вопросу провел Буссинеcко для жесткого круглого
штампа
Ео – модуль деформации грунта
l – полудлина фундамента (балки)
Е1
– модуль упругости материала фундаментаh1 – высота фундамента