МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ МОСКОВСКИЙ

Кафедра «Динамика, прочность машин и сопротивление материалов»
Тема 3. Линейная

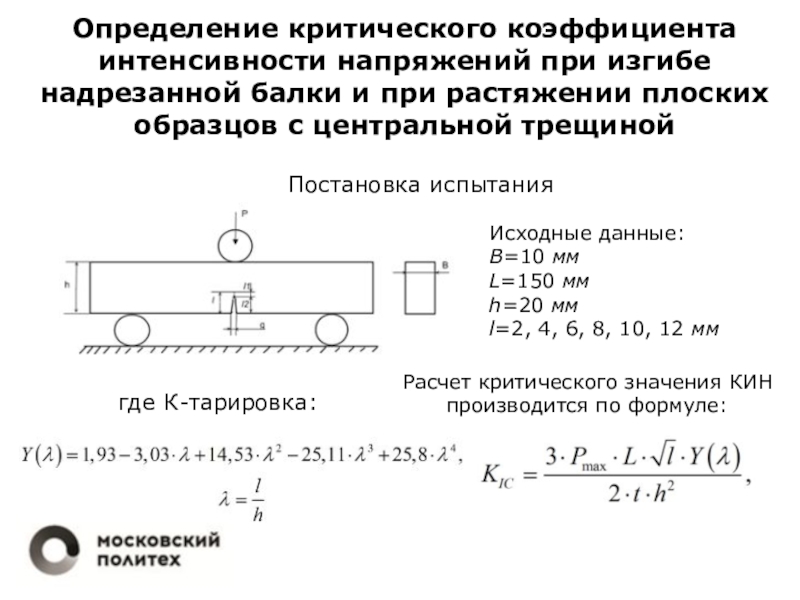
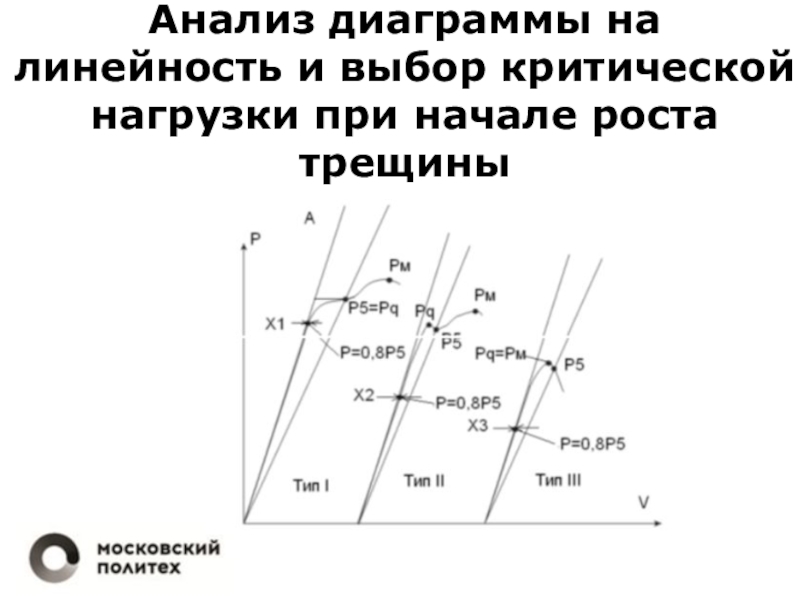
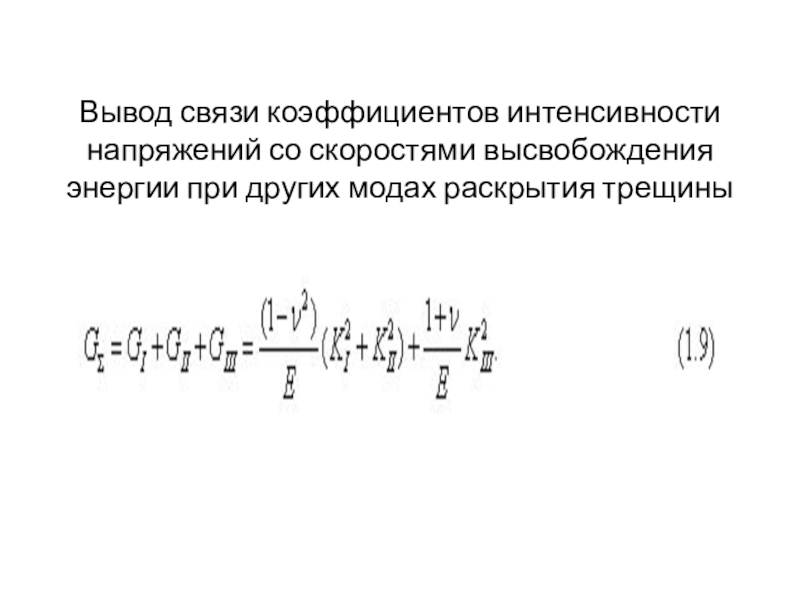
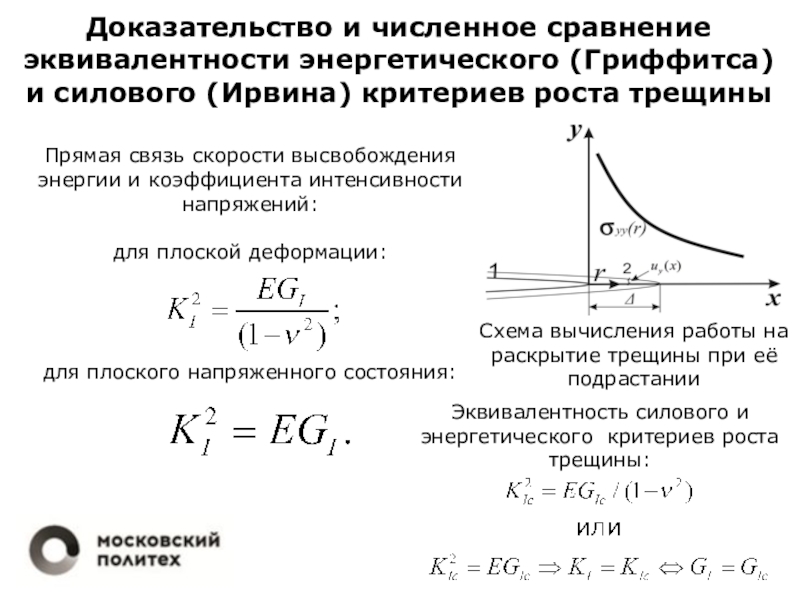
механика разрушения
Семинар 3.2. Оценка КИН методом сечений, экспериментально и с помощью МКЭ. Решение практических задач по анализу хрупкой прочности.

Дисциплина «Основы физики прочности и механики разрушения»

Лектор:
д.т.н., профессор
Полилов А.Н.

Москва, 2020

податливости для определения критической скорости высвобождения энергии, а также метод

экспериментального определения КИН. Доказана эквивалентность энергетического (Гриффитса) и силового (Ирвина) критериев роста трещины – в линейно упругой постановке задачи.

к линейности диаграммы и к размерам образцов.

С3.2.2. Решение практических

задач по анализу хрупкой прочности различных конструктивных элементов.
С3.2.3. Инженерный метод сечений для оценки КИН.

С3.2.4. Доказательство и численное сравнение эквивалентности энергетического (Гриффитса) и силового (Ирвина) критериев роста трещины.

диаграммы и к размерам образцов
Трещина получает возможность распространяться тогда, когда:

Интенсивность освобождающей энергии G достигает критического значения.
Коэффициент интенсивности К достигает критического значения.

вблизи вершины трещины:
Модель трещины в виде «математического» разреза
Коэффициентом интенсивности напряжений

(КИН):

КИН при одноосном
равномерном растяжении:

К-тарировка.

(CNT – central notch tension);
б - с боковыми надрезами

(DENT – double edge notch tension);
в – с одной боковой трещиной (SENT – single edge notch tension)

Образец в виде надрезанной балки для испытаний на трехточечный (поперечный) или четырехточечный (чистый) изгиб - (NBB – notched beam bending)

Компактный двухконсольный образец на внецентренное растяжение (CT – compact tension, double cantilever beam – DCB)

внецентренное растяжение

балок, испытываемых на трехточечный изгиб:
и четырехточечный изгиб:

при растяжении плоских образцов с центральной трещиной
Постановка испытания
Исходные данные:
B=10 мм
L=150

мм
h=20 мм
l=2, 4, 6, 8, 10, 12 мм

Расчет критического значения КИН производится по формуле:

где К-тарировка:

В линейном случае поле напряжений около вершины трещины определяется единственным

параметром – коэффициентом интенсивности напряжений:

где r – расстояние от вершины трещины. Если предельный размер пластической зоны мал, то он также определяется критическим КИН и пределом текучести:

роста трещины

касательную ОА к начальному, линейному участку диаграммы.
2. Проводят секущую ОВ

с тангенсом угла наклона на 5% меньшим, чем у ОА: ВН=0,95АН.
3. Проводят секущую ОС с тангенсом угла наклона на 20% меньше начального.

Анализ диаграмм нагружения

разрушения:
при E=21000 кг/мм2

с внутренней (или для пластины со сквозной) трещиной с начальной

длиной

Критическая длина трещины

Расчеты допустимых длин трещин через критический КИН
Непосредственное использование в расчетах

энергетической теории Гриффитса требует анализа напряженного состояния конструкции в целом. В связи с этим английский инженер-механик Ирвин предложил использовать в расчетах единственный локальный параметр трещиностойкости – коэффициент интенсивности напряжений (КИН), представляющий собой коэффициент при сингулярном члене в выражении для напряжений вблизи вершины трещины. Если значение КИН в конструкции такое же, как в испытанном образце, то по условию хрупкого разрушения конструкция и образец равноопасны. Если в конструкции достигается критическое значение КИН, определенное в корректных испытаниях на образцах, то это означает, что конструкция находится в критическом состоянии.

интенсивности напряжений, КИН (англ. Stress Intensity factor) используется в линейной

механике разрушения для описания полей напряжений у вершины трещины. Рост трещины начинается когда КИН достигает критического значения

Три вида роста трещины

трещиной:
КИН для широкой пластины с наклонной трещиной:
Иллюстрация к методу сечений

для определения КИН

накопленной в теле упругой энергии dU достаточно для образования двух

новых поверхностей трещины площадью dS:

толщиной t=1 со сквозной трещиной длиной 2l

состояния это условие принимает вид:

а для плоской деформации:

других модах раскрытия трещины

для материалов с высоким пределом текучести и с низкой трещиностойкостью,

поэтому надо четко сформулировать те ограничения, в рамках которых ЛМР поставляет адекватные результаты.

деформирования
2. Ограниченность деформаций
3. Малый размер пластической зоны по отношению

к длине трещины.
4. Достаточная линейность диаграммы нагружения
5. Достаточно выраженный момент начала роста трещины

размеры образца
Ограничиться испытаниями при низких температурах
Перейти к нелинейной

механике разрушения, к ее более универсальному критерию.

критериев роста трещины
Прямая связь скорости высвобождения энергии и коэффициента интенсивности

напряжений:

для плоской деформации:




для плоского напряженного состояния:

Схема вычисления работы на раскрытие трещины при её подрастании

Эквивалентность силового и энергетического критериев роста трещины:

механики разрушения состоит в учете несингулярных членов в степенном разложении

выражения для напряжений около вершины трещины. Эти несингулярные члены (не обращающиеся в бесконечность в вершине трещины) получили название «Т-напряжения».