Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Множества и операции над ними
Содержание
- 1. Множества и операции над ними
- 2. Понятие множестваИстория развития человечестваСмена законов природыСмена языка математикиСовременный язык математикиЯзык теории множеств
- 3. Исторические личности в развитии математикиГалилео Галилей(1564-1642) – итальянский физик, механик, астроном и математикwww. Vikipedia.ru
- 4. Исторические личности в развитии математикиМухаммед ибн Муса ал-Хорезми(IX в.н.э.) учёныйиз Средней Азииwww. Vikipedia.ru
- 5. Множество
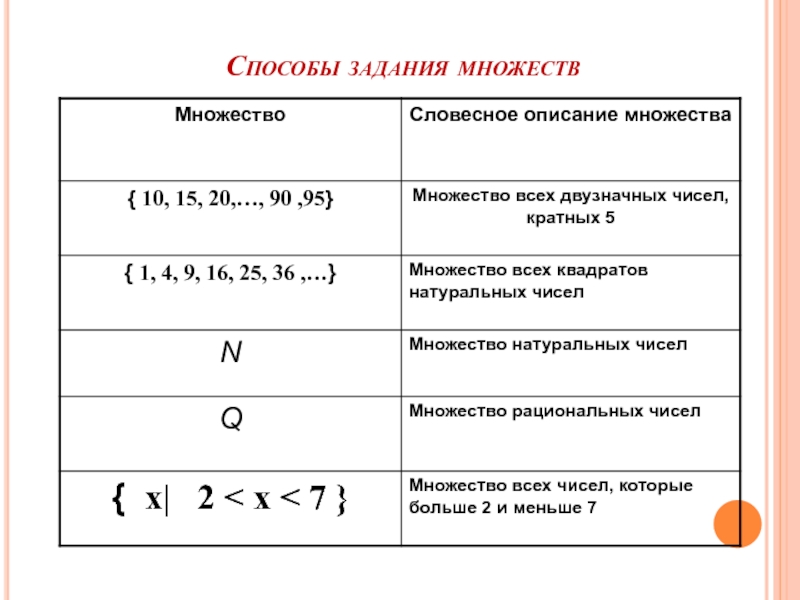
- 6. Способы задания множеств
- 7. ПодмножествоЭлементы, образующие множество А, можно объединять не
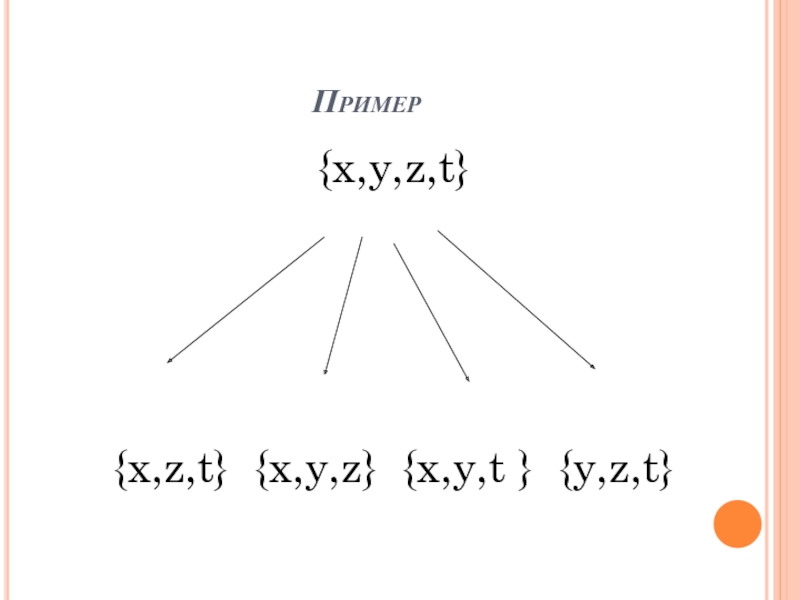
- 8. Пример{x,y,z,t}
- 9. Исторические личности в развитии математики Леонард Эйлер(1707-1783)-швейцарский математикwww. Vikipedia.ru
- 10. Операции над множествамиПересечение множествОбъединение множеств
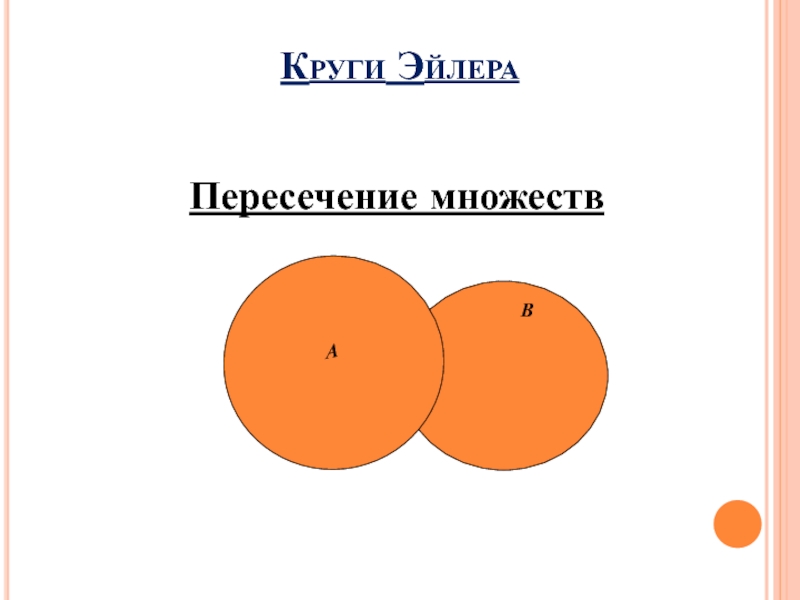
- 11. Круги ЭйлераПересечение множествАВ
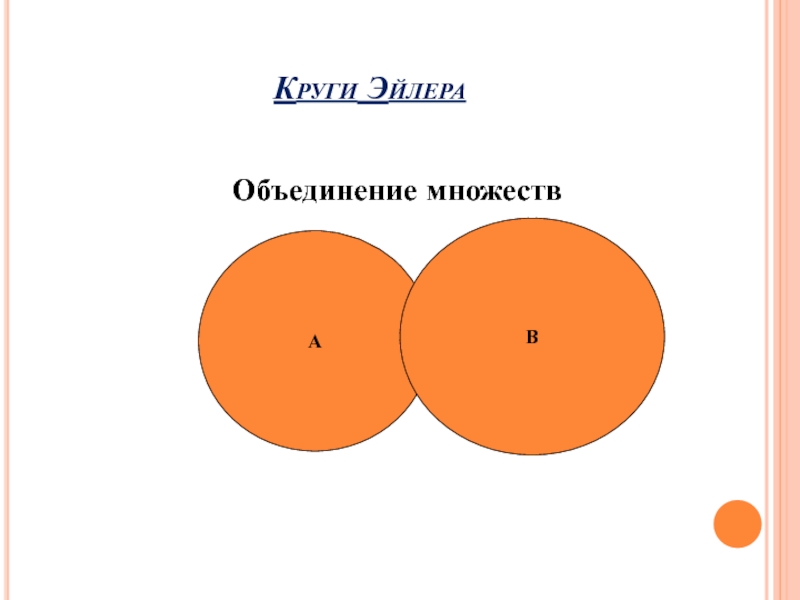
- 12. Круги ЭйлераОбъединение множествАВ
- 13. Слайд 13
- 14. Домашнее задание! § 3,
- 15. Скачать презентанцию
Понятие множестваИстория развития человечестваСмена законов природыСмена языка математикиСовременный язык математикиЯзык теории множеств
Слайды и текст этой презентации
Слайд 2Понятие множества
История развития человечества
Смена законов природы
Смена языка математики
Современный язык математики
Язык
теории множеств
Слайд 3Исторические личности в развитии математики
Галилео Галилей(1564-1642) – итальянский физик, механик,
астроном и математик
www. Vikipedia.ru
Слайд 4Исторические личности в развитии математики
Мухаммед ибн Муса ал-Хорезми(IX в.н.э.) учёный
из
Средней Азии
www. Vikipedia.ru
Слайд 7Подмножество
Элементы, образующие множество А, можно объединять не сразу все вместе,
а группируя их в разных комбинациях.
Если каждый элемент множества В
является элементом множества А, то множество В называют подмножеством множества А.Обозначение: В ϲ А
Слайд 9Исторические личности в развитии математики
Леонард Эйлер(1707-1783)-швейцарский математик
www. Vikipedia.ru
Слайд 14Домашнее задание!
§ 3, определение; замечания; примеры.
№ 3.1; 3.4; 3.6(а);
на повторение: 2.31(г).
