Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Модель Атома по Резерфорду
Содержание
- 1. Модель Атома по Резерфорду
- 2. Рис. 28.1.Альфа-частицы испускались источником 1, помещенным внутри
- 3. происходило дополнительного рассеяния α-частиц в воздухе. Конструкция
- 4. атома. Остальная часть атома представляет собой облако
- 5. которые проходят вблизи от ядра, испытывают резкие
- 6. где r — расстояние между α-частицей и
- 7. Резерфорду удалось вывести формулу, которая связывала число
- 8. экран под определенными углами, сотрудники Резерфорда Гейгер
- 9. Сведения о заряде ядра Ze позволили определить
- 10. электростатического взаимодействия и α-частица на мгновение остановится:Здесь
- 11. обстоятельство, наряду с другими важными причинами, о
- 12. Слайд 12
- 13. Скачать презентанцию
Слайды и текст этой презентации
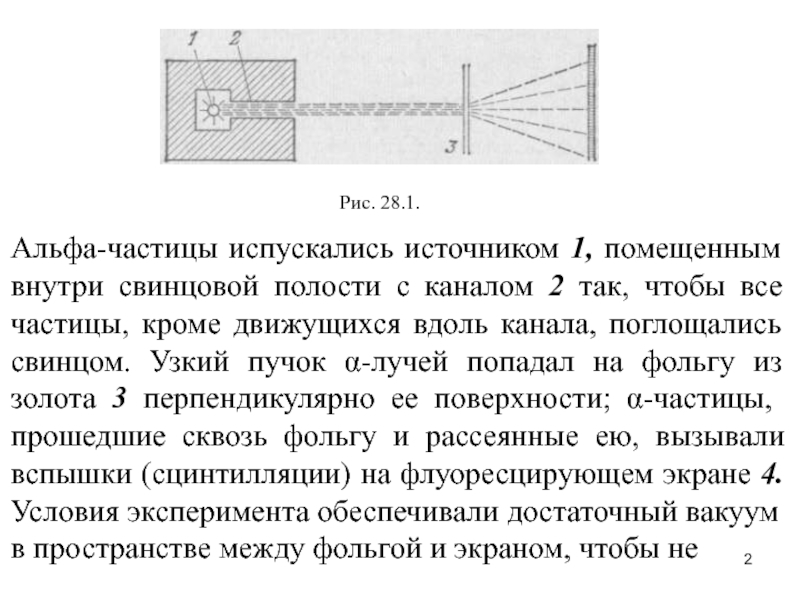
Слайд 2Рис. 28.1.
Альфа-частицы испускались источником 1, помещенным внутри свинцовой полости с
каналом 2 так, чтобы все частицы, кроме движущихся вдоль канала,
поглощались свинцом. Узкий пучок α-лучей попадал на фольгу из золота 3 перпендикулярно ее поверхности; α-частицы, прошедшие сквозь фольгу и рассеянные ею, вызывали вспышки (сцинтилляции) на флуоресцирующем экране 4. Условия эксперимента обеспечивали достаточный вакуум в пространстве между фольгой и экраном, чтобы неСлайд 3происходило дополнительного рассеяния α-частиц в воздухе. Конструкция прибора позволяла наблюдать
α-частицы, рассеянные под углами до 150°.
Опыты показали, что в подавляющем
большинстве случаев α-частицы после прохождения через фольгу сохраняли прежнее направление движения или отклонялись на очень малые углы. Однако некоторые α-частицы отклонялись на большие углы, порядка 135-150°. Объяснить эти резкие отклонения накоплением малых отклонений на пути α-частицы в фольге оказалось невозможным. Для объяснения результатов своих опытов Резерфорд предположил, что весь положительный заряд атома сосредоточен в его ядре — области, занимающей весьма малый объем по сравнению со всем объемомСлайд 4атома. Остальная часть атома представляет собой облако отрицательно заряженных электронов,
полный заряд которых равен положительному заряду ядра. Так в 1911
г. была создана ядерная модель атома, сыгравшая большую роль в развитии современной физики.Результаты опытов Резерфорда получили простое объяснение с точки зрения ядерной модели атома. При прохождении α-частицы сквозь электронную оболочку атома она не должна испытывать заметного отклонения от своего пути. Электроны имеют весьма малую массу по сравнению с массой α-частицы, и отрицательный заряд всех электронов распределен по всему объему электронной оболочки. Поэтому α-частицы, встречающие на своем пути электроны атомов золота, проходят сквозь фольгу, практически не рассеиваясь. Только те α-частицы,
Слайд 5которые проходят вблизи от ядра, испытывают резкие отклонения. На малых
расстояниях силы отталкивания между положительно заряженной α-частицей и массивным ядром
должны быть велики, и это вызывает резкие отклонения таких α-частиц от их первоначальной траектории. Вместе с тем вероятность попадания α-частиц в малое по объему ядро невелика. Поэтому и число α-частиц, испытавших отклонения на большие углы, должно быть весьма невелико.Резерфорд теоретически рассмотрел задачу о движении α-частицы в электрическом кулоновском поле ядра, сосредоточенном в малом объеме. Между α-частицей, заряд которой 2е, и ядром, заряд которого q, действует кулоновская сила отталкивания, равная
Слайд 6где r — расстояние между α-частицей и ядром, ε0— электрическая
постоянная в СИ, е — элементарный электрический заряд. Можно показать,
что под действием силы отталкивания (28.1) α-частица, приближающаяся к ядру, будет отклоняться от него по ветви гиперболы. Это изображено на рис. 28.2. К ядру, находящемуся в точке А, на некотором прицельном расстоянии l приближается α-частица. Под действием силы (27.1) она рассеивается под углом θ и движется по гиперболе. На рис. 27.2 изображено две гиперболические траектории для α-частиц одной и той же энергии при различных значениях прицельного расстояния l.(28.1)
Слайд 7Резерфорду удалось вывести формулу, которая связывала число α-частиц, рассеянных на
определенный угол θ, с энергией α-частиц и числом N положительных
зарядов в ядре. Формула Резерфорда допускала экспериментальную проверку при опытах с заданной энергией α-частиц. Подсчитывая число α-частиц, падавших наРис. 28.2
Слайд 8экран под определенными углами, сотрудники Резерфорда Гейгер и Марсден в
1913 г. в опытах с золотыми и серебряными фольгами подтвердили
теорию Резерфорда. При этом им удалось показать, что q/e приблизительно равняется половине массового числа. Несколько позднее Чэдвик в более совершенных опытах с медными, серебряными и золотыми фольгами показал, что q/e очень близко к порядковому атомному номеру Z в периодической системе Менделеева: q=Ze. Таким образом, идея Резерфорда о ядерной модели атома получила блестящее экспериментальное подтверждение и позволила установить физический смысл порядкового номера в периодической системе элементов.Слайд 9Сведения о заряде ядра Ze позволили определить размеры области, занятой
ядром атома,— верхний предел «радиуса» ядра. Слово «радиус» поставлено в
кавычки не случайно. Столкновение α-частицы с ядром нельзя рассматривать как соударение двух упругих шаров. Если считать, что и ядро, и α-частица имеют сферическую форму, то сумма их радиусов окажется меньшей, чем то минимальное расстояние d, на которое они могут сблизиться при наличии силы отталкивания. Предположим, что между α-частицей и ядром происходит центральное соударение. Из закона сохранения энергии следует, что на расстоянии d наибольшего сближения с ядром кинетическая энергия α-частицы полностью перейдет в потенциальную энергию ихСлайд 10электростатического взаимодействия и α-частица на мгновение остановится:
Здесь υ — начальная
скорость α-частицы вдали от ядра. Для α-частиц, испускаемых одним из
радиоактивных атомов, так называемым радием-С, υ =l,9·107 м/с. Для золота (Z=79) по формуле (71.2) можно определить d:(28.2)
d = (2е)·(Ze)/(2πε0mυ2) ≈ 3,1·10-14 м.
Ядро атома золота имеет линейные размеры, меньшие этой величины. Если считать, что электрон — это заряженный шарик, то его «классический радиус» должен иметь такой же порядок величины. Это