Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Модель Рамсея-Касса- Купманса
Содержание
- 1. Модель Рамсея-Касса- Купманса
- 2. Домашнее задание 1
- 3. Функция полезностиМгновенная функция полезности с постоянной эластичностью
- 4. Функция полезностиМежвременная функция полезностиесли n=0где ρ –
- 5. Функция полезностиЕсли n≠0, то LT=(1+n)tL0Тогда (1+n)t ~ ent (опраксимируется)Аналогично для ρ
- 6. Функция полезностиМежвременная функция полезностиили
- 7. Задача 2GRGRmУсловие задачи: y=k0,5n=0,01δ=0,05gA=0,05ρ=0,04Найти:для GR k**, y**, c**, mps**для GRm k**, y**, c**, mps**
- 8. Домашнее задание 2
- 9. Задачи домашнего задания 2Задача 1.Нам известно, что
- 10. Задачи домашнего задания 2Задача 2. Снижение нормы
- 11. Слайд 11
- 12. Задачи домашнего задания 2Задача 3.Введем в модель
- 13. Домашнее задание 3
- 14. Задачи домашнего задания 3Задача 1. Решите задачу максимизации полезностиесли мгновенная функция полезности имеет следующий вид
- 15. Задачи домашнего задания 3Задача 2.Посмотреть, каким образом
- 16. Задачи домашнего задания 3Задача 3.В модели РКК
- 17. Задачи домашнего задания 3Задача 3.
- 18. Скачать презентанцию
Домашнее задание 1
Слайды и текст этой презентации
Слайд 3Функция полезности
Мгновенная функция полезности с постоянной эластичностью замещения
θ - мера
относительной несклонности к риску
Слайд 4Функция полезности
Межвременная функция полезности
если n=0
где ρ – норма дисконтирования полезности
(чем выше ρ, тем ниже домашние хозяйства ценят будущее потребление
по отношению к текущемуСлайд 5Функция полезности
Если n≠0, то LT=(1+n)tL0
Тогда (1+n)t ~ ent (опраксимируется)
Аналогично
для ρ
Слайд 7Задача 2
GR
GRm
Условие задачи:
y=k0,5
n=0,01
δ=0,05
gA=0,05
ρ=0,04
Найти:
для GR k**, y**, c**, mps**
для GRm
k**, y**, c**, mps**
Слайд 9Задачи домашнего задания 2
Задача 1.
Нам известно, что для функции Кобба-Дугласа
в модели Солоу GR mps**=α
Нужно найти mps** для GRm
Слайд 10Задачи домашнего задания 2
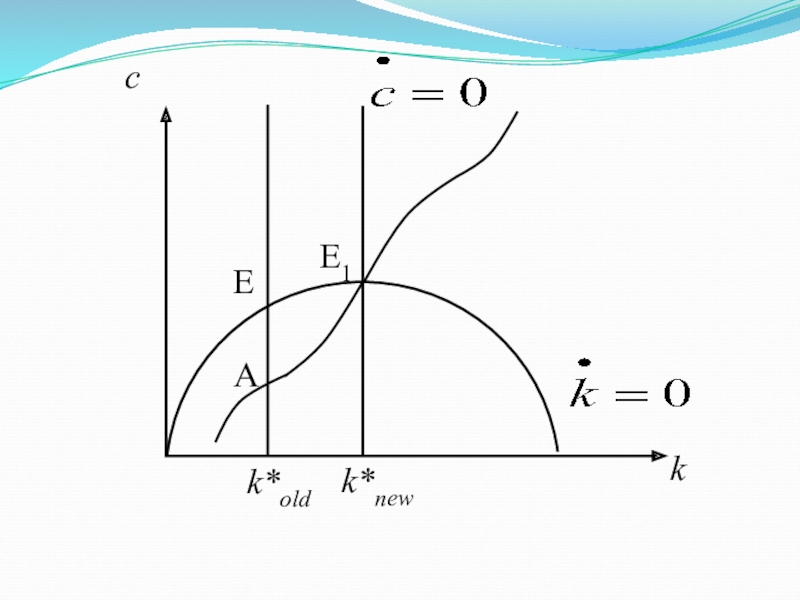
Задача 2. Снижение нормы дисконтирования ρ
Значение k
при котором задается условием
Т.к. то если ρ снижается, k – растет
и кривая сдвигается вправо Слайд 12Задачи домашнего задания 2
Задача 3.
Введем в модель государственные расходы на
закупку товаров и услуг G и пропорциональную налоговую ставку τ,
при этом G = τ·Y, илиСлайд 14Задачи домашнего задания 3
Задача 1. Решите задачу максимизации полезности
если мгновенная
функция полезности имеет следующий вид
Слайд 15Задачи домашнего задания 3
Задача 2.
Посмотреть, каким образом определяется скорость сходимости
в модели РКК
Предположим, что α=1/3, ρ=4%, n=2%, gA=1%, σ=1, амортизация
отсутствуетОпределите на ТСР ставку процента, норму сбережения, скорость сходимости и сравните скорость сходимости при тех же параметрах в модели Солоу.
Слайд 16Задачи домашнего задания 3
Задача 3.
В модели РКК на ТСР рассмотрите
с помощью фазовой диаграммы снижение gA.
Как изменится ли положение кривой
? Как изменится ли положение прямой ?
Что произойдет с в момент сокращения темпов роста производительности?