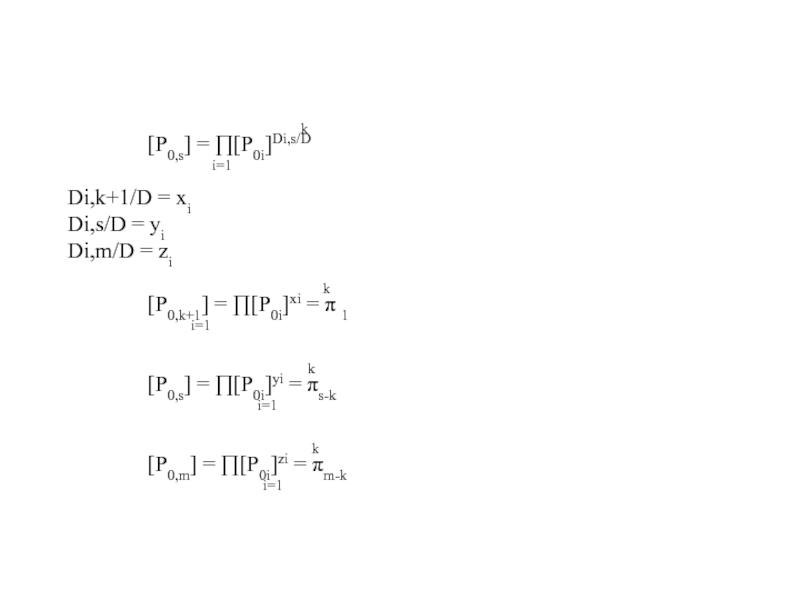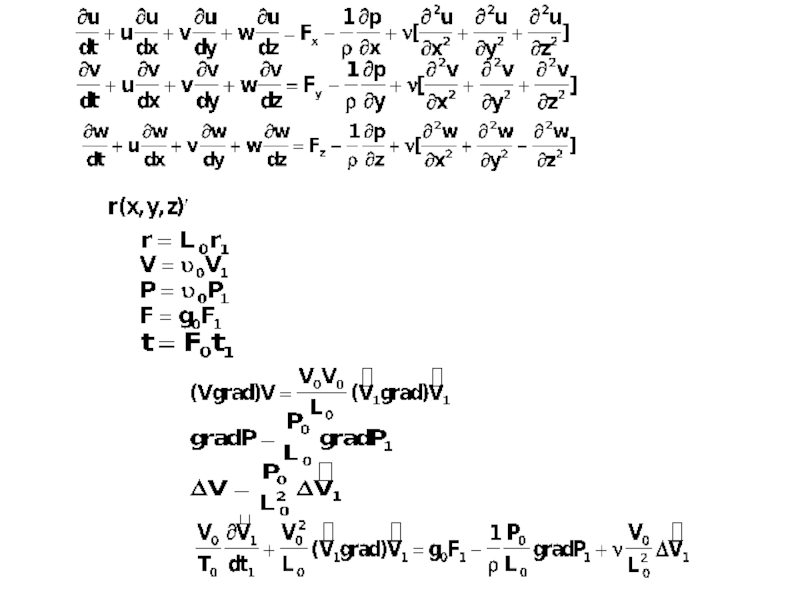Слайд 1
Теория подобия и моделирования.
Подобие
Подобие Подобие геометрическое скоростей и ускорений динамическое
- критерий подобия; безразмерная величина; отношение размерных величин
M = v/a- число Маха, отношение скорости объекта к скорости звука.
Если М<1, то работает докритическое течение.
При М>1 происходят скачки уплотнения.
Скачок уплотнения -характерная для сверхзвукового течения область, в которой происходит резкое увеличение давления, плотности, температуры и уменьшение скорости течения газа. В ряде случаев тождествен ударной волне.
М=1- граница между событиями, надкритическое течение.
Докритическое и надкритическое течения качественно отличаются.
Слайд 2Турбулентное и ламинарное течение
Критерий Рейнольдса
Re = dw/
d -
диаметр;
w - скорость потока;
- плотность;
- динамическая вязкость.
Труба и движение вещества.
w d Ламинарное течение (слоистое).
Линейная зависимость между P и Q.
w d Турбулентное течение.
Нелинейная зависимость между P и Q.
Если Re < 2300, то ламинарное течение;
Re > 2300, то турбулентное течение.
Слайд 3Турбулентность
Турбуле́нтность (лат.. turbulentus — бурный, беспорядочный)- явление, заключающееся в том, что, обычно,
при увеличении скорости течения жидкости или газа в среде самопроизвольно
образуются многочисленные нелинейные фрактальные волны и обычные, линейные различных размеров, без наличия внешних, случайных, возмущающих среду сил и/или при их присутствии. Волны появляются случайно, и их амплитуда меняется хаотически в некотором интервале. Возникают чаще всего либо на границе, у стенки, и/или при разрушении или опрокидывании волны. Могут образоваться на струях. Экспериментально турбулентность можно наблюдать на конце струи пара из электрочайника. Количественные условия перехода к турбулентности были экспериментально открыты английским физиком и инженером О. Рейнольдсом в 1883г. при изучении течения воды в трубах.
До настоящего момента не получено ни одного точного аналитического решения этой системы уравнений Навье-Стокса для турбулентной области течения.
Обычно турбулентность наступает при превышении критической величины неким параметром, например, числом Рейнольдса.
Слайд 4Динамические аналогии
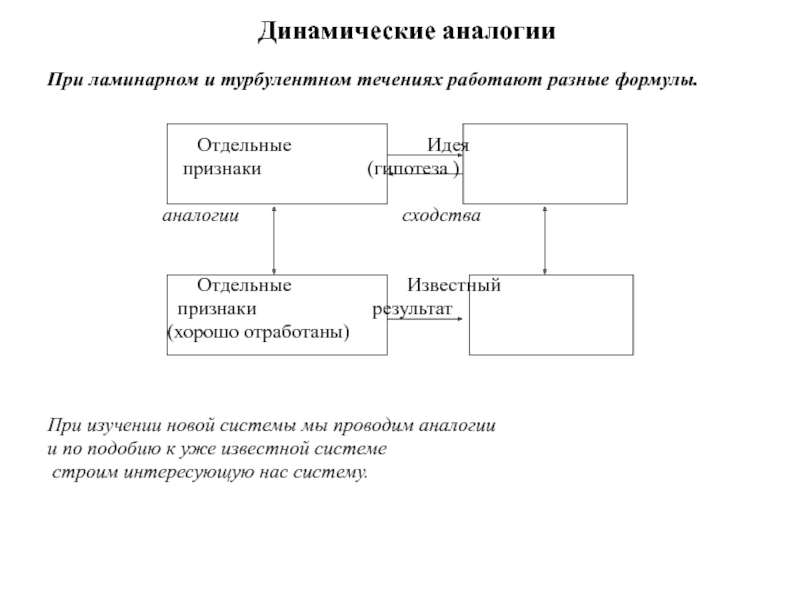
При ламинарном и турбулентном течениях работают разные формулы.
Отдельные Идея
признаки (гипотеза )
аналогии сходства
Отдельные Известный
признаки результат
(хорошо отработаны)
При изучении новой системы мы проводим аналогии
и по подобию к уже известной системе
строим интересующую нас систему.
Слайд 5
Методы получения критериев подобия.
Метод основан на использовании:
а). - теоремы
(теоремы Букингема)
б). Метода интегральных аналогов
В основе лежит теория размерности.
A =
{A}[A]
[A] - единицы размерности, т.е.
A = {30}[км/час]
Есть единицы основные и произвольные.
Слайд 6Пример
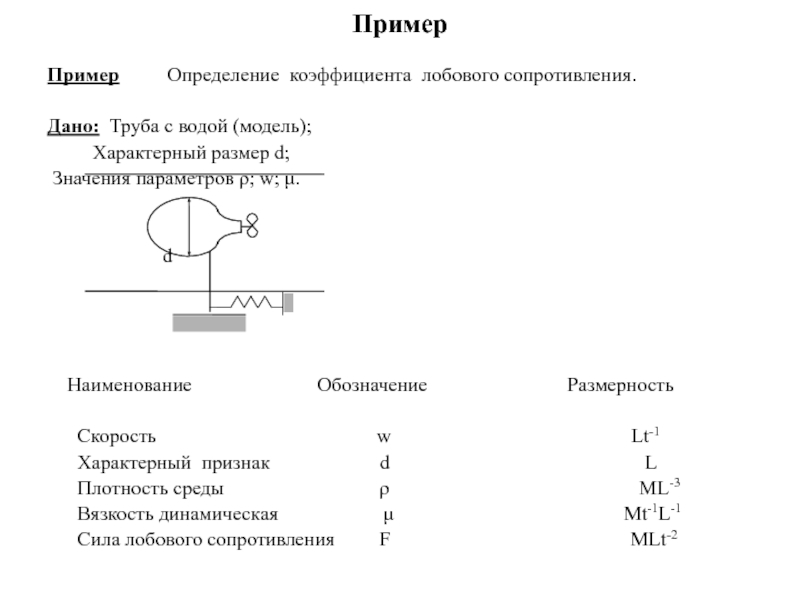
Пример Определение коэффициента лобового сопротивления.
Дано: Труба с водой (модель);
Характерный размер d;
Значения параметров ; w; .
d
Наименование Обозначение Размерность
Скорость w Lt-1
Характерный признак d L
Плотность среды ML-3
Вязкость динамическая Mt-1L-1
Сила лобового сопротивления F MLt-2
Слайд 7Есть некая функция, которая определяет силу лобового сопротивления как
(wa, db,
c, λ) = F
Определим размерность
([Lt-1]a, [L]b, [ML-3]c, [Mt-1L-1] λ)
= [MLt-2]
M: c + λ = 1
L: a + b - 3c - λ = 1
t: - a - λ = -2
Решаем систему уравнений и получаем
c = 1 - λ
a = 2 - λ
2 - λ + b - 3 + 3 λ - λ = 1
b = 2 - λ
Перепишем исходную формулу в несколько ином виде
(w2- λ, d2- λ, 1- λ, λ) = F
т.е. можем записать
F/w2d2 = (/wd) = (1/Re)
- теорема
Всякое полное уравнение физического процесса записанное в определенной системе единиц может быть представлена в виде зависимости между критериями подобия, т.е. безразмерных соотношений, составленных из входящих в уравнение переменных и параметров.
f(P1, P2,..., Pi,..., Pk,..., Ps,..., Pm) = 0
1 i k k+1 s m f(P1/P01;P2/P02,...;Pi/P0i,...;Pk/P0k,...;Ps/P0s,...;Pm/P0m)=0
Основные и производные единицы. Производные можно выразить через основные.
Для этого надо:
а) Выбрать те параметры, которые являются независимыми.
Б) Выразить зависимые через независимые. Имеем матрицу размерностью [mn], в которой число строк больше числа столбцов (m > n).
Ранг не больше n.
Слайд 9Пусть
P1,..., Pk - независимые параметры;
Pk+1,..., Pm - зависимые параметры.
Pk+1,...,
Pm. следует выразить через P1,..., Pk
Тогда
получим
f(1,...,1, 1,..., s-k,..., m-k) = 0
Каждый параметр P выражается в виде
Р = {Р}[Р]
где {Р}- число, [Р] - размерность.
[P1] = [a1, b1,..., q1] = [P01]
[P2] = [a2, b2,..., q2] = [P02]
. . . . . . . . . . .
[Pi] = [ai, bi,..., qi] = [P0i]
. . . . . . . . . . .
[Pk] = [ak, bk,..., qk] = [P0k]
k q
q - количество независимых параметров.
Слайд 10[P0,k+1] = k+1{[P01],...,[P0k]}
. . . .
. . . . .
.
[P0,s] = s{[P01],...,[P0k]}
. . . . . . . . . .
[P0,n] = n{[P01],...,[P0k]}
Определим зависимости k+1,...,s,...,n
ln[P01] = 1ln[a] + 1ln[b] +...+ 1ln[q]
ln[P02] = 2ln[a] + 2ln[b] +...+ 2ln[q]
. . . . . . . . . . . . . . .
ln[P0k] = kln[a] + kln[b] +...+ kln[q]
1 1 ... 1 ln[P01]
2 2 ... 2 = D ln[P02]
. . . . . . . .
k k ... k ln[P0k]
D - определитель
ln[a] = (ln[P01])A11/D(ln[P02])A21/D...(ln[P0k])Ak1/D
Ak1 - определить получаемый из определителя D путем вычеркивания k-ой строки и 1-го столбца.
k
ln[a] = (Ai1/D)ln[P0i]
i=1
Слайд 11Пусть k = q
ln[a] =
ln[b] =
. .
. .
ln[q] =
Определяем [a],[b],...,[q]
[a] = [P01]A11/D[P02]A21/D...[P0k]Ak1/D
[b] =
.
. .
[q] =
Полученные выражения подставим в формулы
[P0,k+1] = [P01]D1,k+1/D[P02]D2,k+1/D... [P0k]Dk,k+1/D
. . . . . . . . . .
[P0,s] = [P01]D1,s/D[P02]D2,s/D... [P0k]Dk,s/D
. . . . . . . . . .
[P0,m] = [P01]D1,m/D[P02]D2,m/D... [P0k]Dk, m/D
Di,k+1 - определитель, в котором i-ая строка заменена (k+1) строкой из формул размерности.
k
[P0,s] = [P0i]Di,s/D
i=1
Di,k+1/D = xi
Di,s/D = yi
Di,m/D = zi
k
[P0,k+1] = [P0i]xi = 1
i=1
k
[P0,s] = [P0i]yi = s-k
i=1
k
[P0,m] = [P0i]zi = m-k
i=1
Слайд 13Пусть
P1 = P01
P2 = P02
.
. . .
Pk = P0k
k k k
f(1,...,1, Pk+1/[P0i]xi,...,Ps/[P0i]yi,..., Pm/[P0i]zi) = 0
i=1 i=1 i=1
f(1,...,1, 1,..., s-k,..., m-k)
1 = (2,..., m-k)
Реальность Модель
1 1
2
. . . . . .
m-k m-k
P1, P2,...,Pk,...,Pm
- подобие сил.
Слайд 14Планирование эксперимента;
основные понятия
Слайд 15 Планирование эксперимента
Основные понятия.
- Активный эксперимент
-
Пассивный эксперимент
Основная идея активного эксперимента - добиться требуемых
свойств, выбирая условия проведения эксперимента.
1. План эксперимента X
1 j n 1 i N
n - число факторов, N - число экспериментов
xi = (x1i, x2i,..., xni)
x11, x21,..., xn1
X = xji = x12, x22,..., xn2
. . . . . .
x1N, x2N,..., xnN
2. Центр плана
. . +1, -1
. .
3.Центральный план
- это план, в котором центр расположен в начале координат.
Слайд 164. Область определения. Нормированные переменные.
Пусть
xj- реальные факторы
xj - нормированные факторы
-1 xj 1 1 j
n
n - факторы
Надо определить xjmin и xjmax
xj = [xj- (xjmin + xjmax)/2] / [(xjmax - xjmin)/2]
5. Матрица M = FF
y = a0 + a1x1 + a2x2 +... + anxn
1 план
1 экспе-
f = 1 римен-
1 та
1
Слайд 17М - информационная матрица плана X размерности (k+1)(k+1)
det(A-I) = 0
где
- корни характеристического уравнения.
0
M =
0
План X,
которому соответствует диагональная информационная матрица, называется ортогональным.
Если при применении МНК какие-либо коэффициенты а оказываются незначимыми, то в общем случае необходимо произвести перерасчет коэффициентов для новой модели.
Если использовался критерий ортогональности плана, то замена на 0 любого коэффициента в уравнении модели не изменит оценок других коэффициентов.
Преимущества ортогонального плана:
а) упрощение вычислений
б) независимые коэффициенты оценок
6. Свойство ротатабельности
План X является ротатабельным, если дисперсия оценки зависит только от расстояния точки x от центра плана.
Слайд 18Пример
Пусть модель
y(a,x) = a0 + a1x1 + a2x2 +...
+ anxn
x0 = 0 - центр плана
M = 4I3
f(x) = (1, x1, x2)
= (1, x1, x2)(1/4)I3 = (1/4)(1+ x12 + x22) =
= (1/4)(1+r2)
Дисперсия всех равноудаленных точек одинакова.
7. План X называется ненасыщенным , если N > k+1;
насыщенным , если N = k+1
Слайд 198. Критерий планирования эксперимента.
План эксперимента зависит от выбранного
критерия. Критерий в основном определяет либо требования к модели, либо
требования к точности.
Кроме критериев ортогональности и ротатабельности назовем критерии А-оптимальности и Д-оптимальности.
Критерий А-оптимальности требует такого выбора плана X, при котором матрица C имеет минимальный след (т.е. сумма диагональных элементов минимальна). Практически это означает минимизацию средней дисперсии оценок коэффициента а.
Критерий D-оптимальности требует такого расположения точек, при котором определитель матрицы C минимален.
Слайд 20Полный (простой) факторный эксперимент.
Факторы - число n (n=3)
Уровни (2) - (значения
факторов - +1, -1 )
2n - полный факторный
эксперимент
2n-р - дробный эксперимент, где р -число генераторов
Пусть есть факторы x1,x2,x3
x1 x2 x3 = x1x2 n=3 p=1
1 1 1 23-1=4 (вместо восьми)
1 -1 -1
-1 1 -1
-1 -1 1
Слайд 21 Планы для квадратичных моделей.
Композиционный план второго порядка
y = a0 +
a1x1 + a2x2 + a3x3 + a4x12 + a5x22 +
a6x32 +
+ a7x1x2 + a8x1x3 + a9x2x3
(n+1)(n+2)/2 = 10 - количество коэффициентов.
x1 x2 x3
1 1 1 1
2 1 1 -1
3 1 -1 1 23 = 8
4 1 -1 -1
5 -1 1 1
6 -1 1 -1
7 -1 -1 1
8 -1 -1 -1
9 0 0 0 - центр плана
10 + 0 0
11 - 0 0
12 0 + 0 - 2n звездных точек
13 0 - 0
14 0 0 +
15 0 0 -
Звездные точки обычно выбирают так,
чтобы обеспечить ортогональность получаемого плана.
Слайд 22Понятие рандомизации.
Рандомизация заключается в том, что планируемые опыты
выписываются в логическом порядке, а затем их номера случайным образом
перемешиваются. И именно в таком случайном порядке они и производятся.
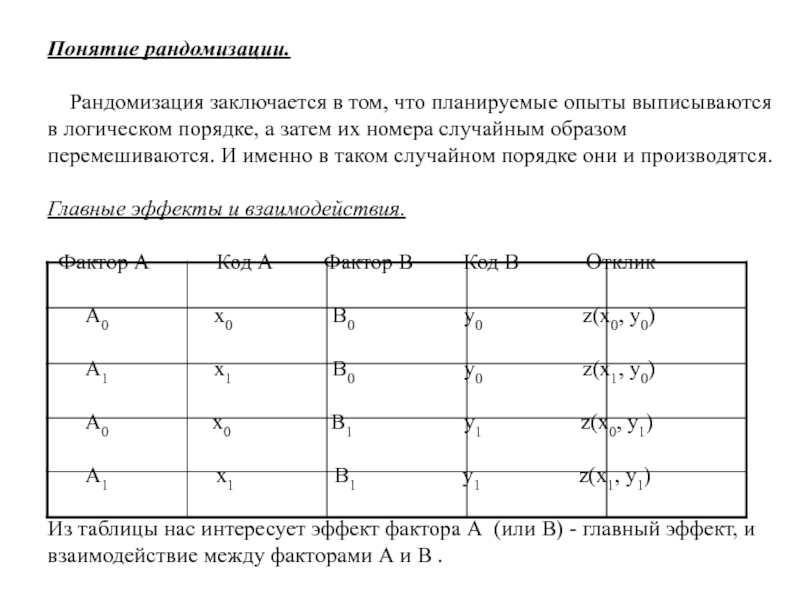
Главные эффекты и взаимодействия.
Фактор А Код А Фактор В Код В Отклик
A0 x0 B0 y0 z(x0, y0)
A1 x1 B0 y0 z(x1, y0)
A0 x0 B1 y1 z(x0, y1)
A1 x1 B1 y1 z(x1, y1)
Из таблицы нас интересует эффект фактора А (или В) - главный эффект, и взаимодействие между факторами А и В .
Слайд 23Главный эффект фактора А пропорционален разности между:
а) средним значением по
всем откликам, включающим обработку фактора А на верхнем уровне (А1).
б)
средним значением по всем откликам из комбинации обработок, включающих нижний уровень фактора А (А0).
А = [z(x1, y0) + z(x1, y1)]/2 - [z(x0, y0) + z(x0, y1)]/2
аналогично для В
- определяется какой из факторов весомее.
Эффект взаимодействия между А и В пропорционален разности между:
а) эффектом увеличения А при В, зафиксированном на верхнем уровне;
б) эффектом увеличения А при В, зафиксированном на нижнем уровне.
Пусть
число уровней - 4; число факторов - 3;
Тогда число опытов - 43 = 64.
Слайд 24 Греко-латинские квадраты.
Латинский квадрат.
Пусть имеются 3 фактора - P,
L, S, и 4 уровня - i = 1, 2,
3, 4.
P1 P2 P3 P4
L1 S1 S2 S3 S4 В каждой строке и в каждом столбце Si L2 S2 S3 S4 S1 встречается только один раз.
L3 S3 S4 S1 S2 16 вместо 64.
L4 S4 S1 S2 S3
Греко-латинский квадрат - это то же самое, что латинский, но с обобщением на 4 фактора.
A B C D
B C D A
C D A B
D A B C
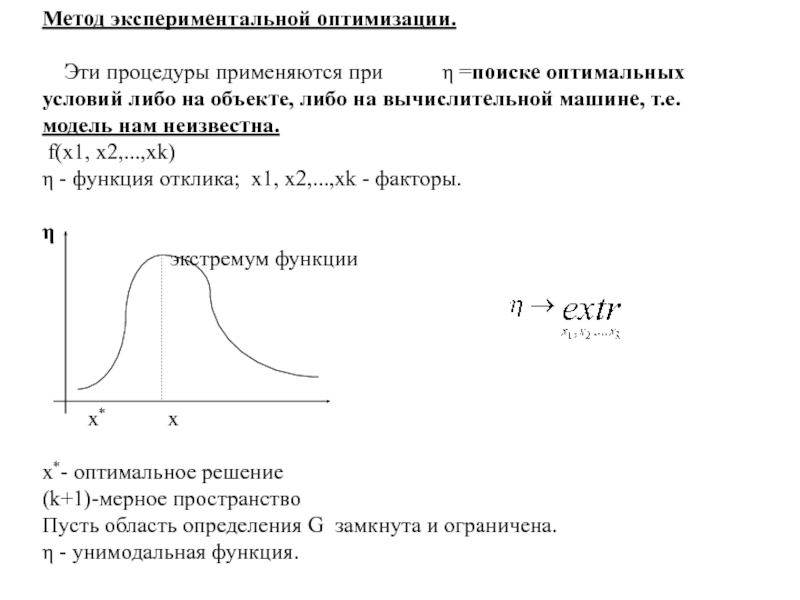
Слайд 25Метод экспериментальной оптимизации.
Эти процедуры применяются при =поиске
оптимальных условий либо на объекте, либо на вычислительной машине, т.е.
модель нам неизвестна.
f(x1, x2,...,xk)
- функция отклика; x1, x2,...,xk - факторы.
экстремум функции
x x
x- оптимальное решение
(k+1)-мерное пространство
Пусть область определения G замкнута и ограничена.
- унимодальная функция.
Слайд 26 Метод Бокса-Уилсона.
Идея метода заключается в использовании метода крутого
восхождения в сочетании с последовательно планируемым факторным экспериментом для нахождения
оценки градиента.
Процедура состоит из нескольких повторяющихся этапов:
- построение факторного эксперимента в окрестностях некоторой точки;
- вычисление оценки градиента в этой точке по результатам эксперимента;
- крутое восхождение в этом направлении;
- нахождение максимума функции отклика по этому направлению.
Допущения:
- функция отклика непрерывна и имеет непрерывные частные производные на множестве G ;
- функция унимодальная (т.е. экстремум - внутренняя точка).
Слайд 27
m – номер итерации
α влияет на шаг.
- оператор Набла
Δх нужно
подсчитать
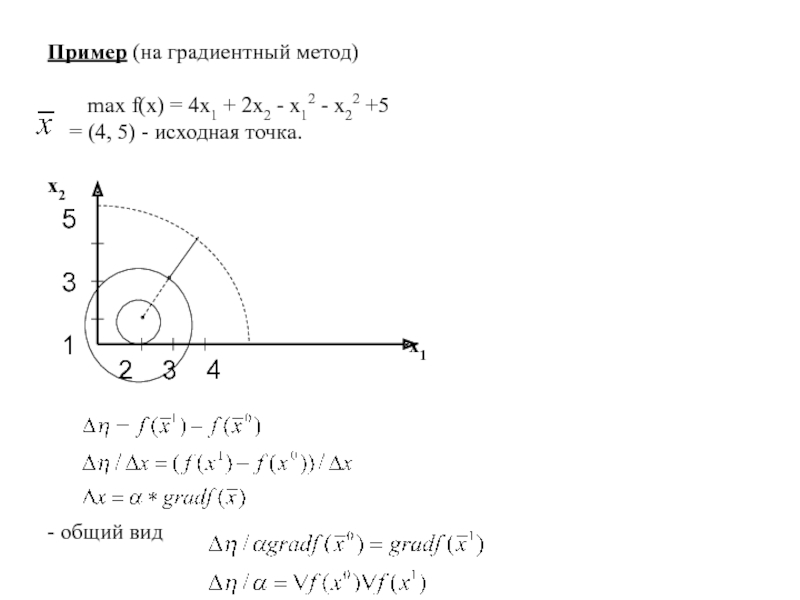
Слайд 28Пример (на градиентный метод)
max f(x) = 4x1 + 2x2 -
x12 - x22 +5
= (4, 5) - исходная
точка.
х2
х1
- общий вид
Слайд 29
f/x1 = 4 - 2x1
f/x2 = 2 - 2x2
f(x0) =
(4-24, 2-25) = (-4, -8)
- градиент в точке x0
Вторая итерация
т.е.
точка - решение задачи
Слайд 30Оценивание градиента.
Если функция (x1, x2,..., xk),
где x1,
x2,..., xk - размерные величины, то перейдем к безразмерному виду:
f(x1,
x2,..., xk),
где x1, x2,..., xk - безразмерные величины.
Разложим эту функцию в ряд Тейлора в точке 0.
Для линейной зависимости.
f(x1, x2,..., xk) = a0 + a1x1 + a2x2 +...+ akxk
где
ai = f/xi i = 1…k i 0
a0 = f(x10, x20,..., xk0)0
Слайд 31
x2
x1
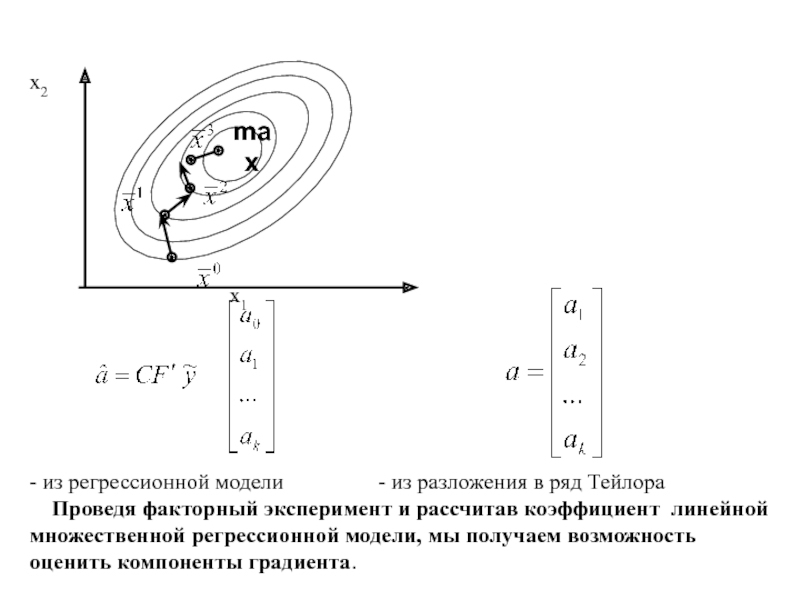
- из регрессионной модели
- из разложения в ряд Тейлора
Проведя
факторный эксперимент и рассчитав коэффициент линейной множественной регрессионной модели, мы получаем возможность оценить компоненты градиента.
Слайд 32 Метод интегральных аналогов.
Для получения критериев подобия по методу
интегральных аналогов необходимо знать уравнения системы или процесса.
Если все члены уравнения разделить на один из них, то получим уравнение в безразмерной форме (Фурье - все члены уравнения имеют одну и ту же размерность).
Пример
Уравнение Навье-Стокса.
V- скорость потока в точке.
F - объемная или массовая сила
Р - давление
- плотность жидкости
- кинетическая вязкость
- лапласиан или дифференциальный оператор второго порядка
- оператор набла
=
- скалярное произведение
Слайд 34
Пренебрегаем индексом 1; Разделим члены уравнения на
- число подобия Струхаля
- число подобия Фруда
- число подобия Эйлера
- число подобия Рейнольдса
Слайд 35Фракталы.
Размерность Хаусдорфа-Безиковича.
Слайд 36Введение
Автор понятия и первых работ по фрактальной геометрии Бенуа Мандельброт
Нестрогое
определение: Фрактал - это структура, состоящая из частей, которые в
каком-то смысле подобны целому.
Большинство структур, которые мы можем вычленить из реальных объектов, обладают свойством геометрической регулярности или самоподобием, что проявляется в их инвариантности по отношению к масштабу
Автор понятия и первых работ по фрактальной геометрии Бенуа Мандельброт
Нестрогое определение: Фрактал - это структура, состоящая из частей, которые в каком-то смысле подобны целому.
Большинство структур, которые мы можем вычленить из реальных объектов, обладают свойством геометрической регулярности или самоподобием, что проявляется в их инвариантности по отношению к масштабу
Слайд 37IFS (Iterated Functions Systems)
Kern: xk+1= Fx (xk, yk)
yk+1= Fy (xk,
yk)
Mandel / Julia zk+1=zk2+z0 (z0=c0)
Слайд 40Неформально о размерностях
Топологическая размерность:
принимает исключительно целые значения
размерность одноточечного множества равна
нулю, отрезка и прямой - единица, размерность n-мерного куба равна
n
Проблемы топологической размерности
Размерность Хаусдорфа-Безиковича – обобщение, геометрический смысл







![Теория подобия и моделирования [P0,k+1] = k+1{[P01],...,[P0k]} . . . . . . . [P0,k+1] = k+1{[P01],...,[P0k]} . . . . . . .](/img/thumbs/b778229f8b5c029fcbea19b6f41cb9bc-800x.jpg)
![Теория подобия и моделирования Пусть k = q ln[a] = ln[b] = . . Пусть k = q ln[a] = ln[b] = . . . . ln[q]](/img/thumbs/fc545bf1a0a695b63c0ef90252da82d8-800x.jpg)