Слайд 1№ 24-25 Дәріс
Тақырыбы:
Регрессиялық талдау
Слайд 2Дәріс жоспары:
Регрессиялық талдау: негізгі түсініктер.
Регрессия түрлері.
Сызықты регрессия параметрлерін ең кіші
квадраттар әдісі бойынша бағалау.
Регрессия коэффициентінің маңыздылығы туралы болжамды тексеру.
Регрессия
теңдеуінің маңыздылығы туралы болжамды тексеру.
Детерминация коэффициенті.
Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы.
Слайд 3Регрессиялық талдау
«Регрессия» терминін алғаш рет биометрияның негізін салушы Ф. Гальтон
енгізген, оның ойын ізбасары К. Пирсон дамытқан.
Ф. Гальтон
(1822—1911)
К. Пирсон
(1857—1936)
Регрессиялық
талдау - бір немесе бірнеше белгілердің (факторлық белгілердің) және салдардың (нәтижелі белгілердің) арасындағы байланысты өлшеуге мүмкіндік беретін статистикалық өңдеу әдісі.
Слайд 4Регрессиялық талдау: негізгі түсініктер
Белгі – бұл зерттелетін құбылыстың немесе үдерістің
негізгі ерекшелігі.
Нәтижелік белгі – зерттелелетін көрсеткіш.
Факторлық белгі - нәтижелік белгінің
мәніне әсер ететін көрсеткіш.
Регрессиялық талдаудың мақсаты регрессия теңдеуі түрінде берілген орташа мәннің (у) нәтижелік белгісінің, (х1, х2, …, хn), факторлық белгіге функционалдық байланысын бағалау болып табылады:
Слайд 5Регрессиялық талдау: негізгі түсініктер
Регрессия
Жұптасқан
у = f (x)
КӨПШЕ
Регрессиялық талдау келесі кезеңдерден
тұрады:
функция түрін анықтаудан;
регрессия коэффициенттерін анықтаудан;
нәтижелі белгінің теориялық мәндерін есептеуден;
регрессия коэффициентінің
статистикалық маңыздылығын тексеруден;
регрессия теңдеуінің статистикалық маңыздылығын тексеруден.
Слайд 6Дәріс жоспары:
Регрессиялық талдау: негізгі түсініктер.
Регрессия түрлері.
Сызықты регрессия параметрлерін ең кіші
квадраттар әдісі бойынша бағалау.
Регрессия коэффициентінің маңыздылығы туралы болжамды тексеру.
Регрессия
теңдеуінің маңыздылығы туралы болжамды тексеру.
Детерминация коэффициенті.
Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы.
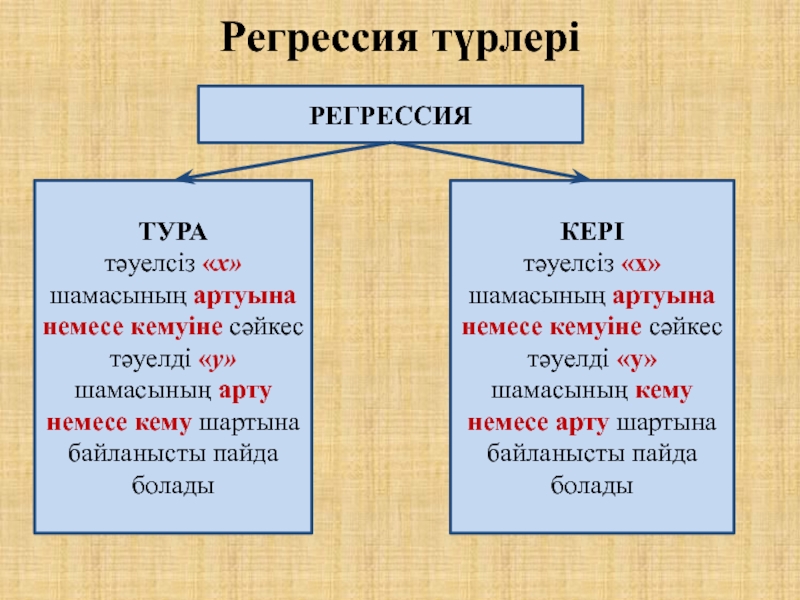
Слайд 7Регрессия түрлері
Регрессия
Тура
тәуелсіз «х» шамасының артуына немесе кемуіне сәйкес тәуелді «у»
шамасының арту немесе кему шартына байланысты пайда болады
КЕРІ
тәуелсіз «х»
шамасының артуына немесе кемуіне сәйкес тәуелді «у» шамасының кему немесе арту шартына байланысты пайда болады
Слайд 8Жұптасқан регрессия теңдеуілер
Байланысты сипаттау үшін келесі жұптасқан регрессия теңдеулерінің түрлерін
қолданады:
у=a+bx – сызықтық;
y=eax+b – экспоненциалды;
y=a+b/x – гиперболалық;
y=a+b1x+b2x2 –
параболалық;
y=abx – көрсеткіштік және т.б.
мұндағы a, b1, b2 - теңдеудің коэффициенттері (параметрлері); у – нәтижелі белгі; х – факторлық белгі.
Слайд 9Дәріс жоспары:
Регрессиялық талдау: негізгі түсініктер.
Регрессия түрлері.
Сызықты регрессия параметрлерін ең кіші
квадраттар әдісі бойынша бағалау.
Регрессия коэффициентінің маңыздылығы туралы болжамды тексеру.
Регрессия
теңдеуінің маңыздылығы туралы болжамды тексеру.
Детерминация коэффициенті.
Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы.
Слайд 10
Сызықты регрессия параметрлерін ең кіші квадраттар әдісі бойынша бағалау
Регрессия теңдеуін
құру, оның коэффициенттерін (параметрлерін) бағалауға алып келеді, ол үшін ең
кіші квадраттар әдісі қолданылады.
Ең кіші квадраттар әдісі: болғанда параметрлерді бағалауға мүмкіндік береді.
Ең кіші квадраттар әдісі бойынша сызықты регрессия у=a+bх теңдеуінің параметрлерін анықтау формуласы:
Слайд 11Дәріс жоспары:
Регрессиялық талдау: негізгі түсініктер.
Регрессия түрлері.
Сызықты регрессия параметрлерін ең кіші
квадраттар әдісі бойынша бағалау.
Регрессия коэффициентінің маңыздылығы туралы болжамды тексеру.
Регрессия
теңдеуінің маңыздылығы туралы болжамды тексеру.
Детерминация коэффициенті.
Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы.
Слайд 12Регрессия коэффициентінің маңыздылығын тексерудің сызбасы
1) Н0: a=0, b=0.
Н1: a≠0, b≠0.
2) р=0,05 – маңыздылық деңгейі.
3)
мұндағы mb, ma - кездейсоқ қателіктер:
4) tкесте(р; f), мұндағы f=n-k-1, n - бақылау саны, k - айнымалылары «х» теңдеудегі параметрлер саны.
5) Егер болса, онда Н0 қабылданбайды, яғни коэффи-циент маңызды.
Егер болса, онда Н0 қабылданады, яғни коэффициент маңызды емес.
Слайд 13Дәріс жоспары:
Регрессиялық талдау: негізгі түсініктер.
Регрессия түрлері.
Сызықты регрессия параметрлерін ең кіші
квадраттар әдісі бойынша бағалау.
Регрессия коэффициентінің маңыздылығы туралы болжамды тексеру.
Регрессия
теңдеуінің маңыздылығы туралы болжамды тексеру.
Детерминация коэффициенті.
Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы.
Слайд 14Регрессия теңдеуінің маңыздылығын тексерудің сызбасы
1) Н0: регрессия теңдеуі маңызды емес.
Н1: регрессия теңдеуі маңызды.
2) р=0,05 – маңыздылық деңгейі.
3)
мұндағы n - бақылау саны; k - айнымалылары «х» теңдеудегі параметрлер саны; у - нәтижелі белгінің нақты мәні; yx - нәтижелі белгінің теориялық мәні; - жұпталған корреляция коэффициенті.
4) Fкесте(р; f1; f2),
мұндағы f1=k, f2=n-k-1- еркіндік дәрежелерінің саны
5) Егер Fесеп>Fкесте, онда регрессия теңдеуі дұрыс таңдалған.
Егер Fесеп
Слайд 15Дәріс жоспары:
Регрессиялық талдау: негізгі түсініктер.
Регрессия түрлері.
Сызықты регрессия параметрлерін ең кіші
квадраттар әдісі бойынша бағалау.
Регрессия коэффициентінің маңыздылығы туралы болжамды тексеру.
Регрессия
теңдеуінің маңыздылығы туралы болжамды тексеру.
Детерминация коэффициенті.
Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы.
Слайд 16 Детерминация коэффициенті
Регрессиялық талдаудың сапалық өлшемінің негізгі көрсеткіші детерминация коэффициенті
(R2) болып табылады
Детерминация коэффициенті «у» айнымалының қандай бөлігі талдауда ескерілгендігін
және талдауға енгізілген фактордың туғызатын әсерін көрсетеді.
Детерминация коэффициенті (R2) [0,1] аралығында мәндерді қабылдайды. Егер R2 ≥0,8 болса, регрессия теңдеуі сапалы болып табылады.
Детерминация коэффициенті корреляция коэффициентінің квадратына тең, яғни:
Слайд 17Дәріс жоспары:
Регрессиялық талдау: негізгі түсініктер.
Регрессия түрлері.
Сызықты регрессия параметрлерін ең кіші
квадраттар әдісі бойынша бағалау.
Регрессия коэффициентінің маңыздылығы туралы болжамды тексеру.
Регрессия
теңдеуінің маңыздылығы туралы болжамды тексеру.
Детерминация коэффициенті.
Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы.
Слайд 18Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы
1 мысал.
Төмендегі берілгендер бойынша регрессия теңдеуін тұрғызу және талдау:
Шешуі.
Корреляция коэффициентін есептеу:
.
Белгілер арасындағы байланыс түзу және қалыпты.
Слайд 19Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы
1 мысал.
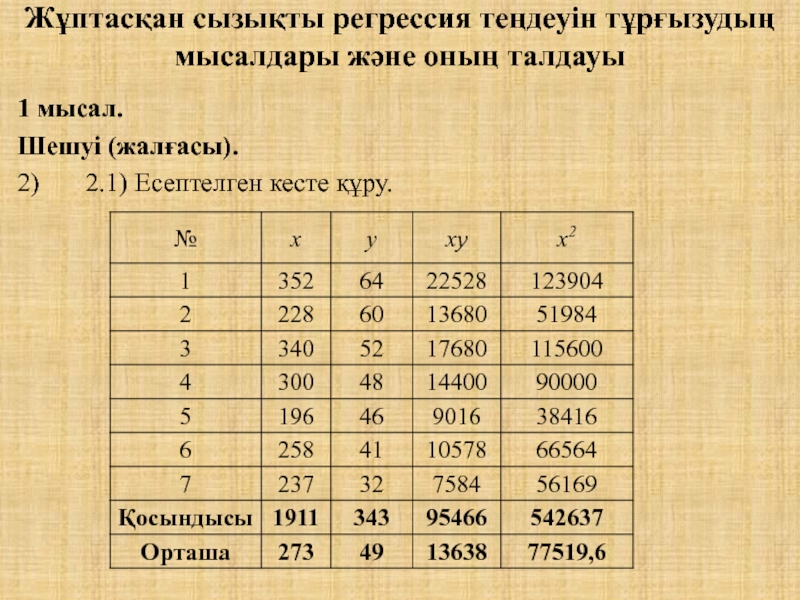
Шешуі (жалғасы).
2) 2.1) Есептелген кесте құру.
Слайд 20Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы
1 мысал.
Шешуі (жалғасы).
2.2) Регрессия коэффициенттерін есептеу:
Жұптасқан сызықты регрессия теңдеуі: ух=25,17+0,087х.
Слайд 21Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы
1 мысал.
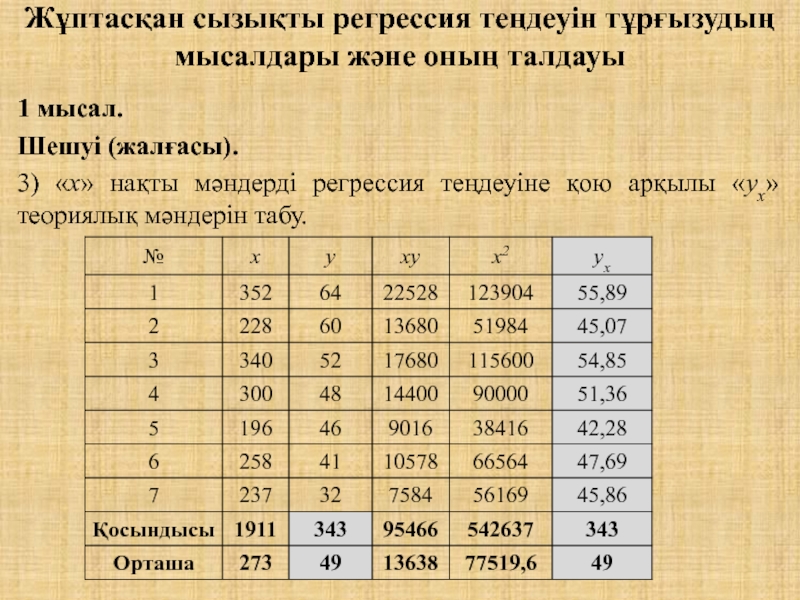
Шешуі (жалғасы).
3) «х» нақты мәндерді регрессия теңдеуіне қою арқылы «уx»
теориялық мәндерін табу.
Слайд 22Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы
1 мысал.
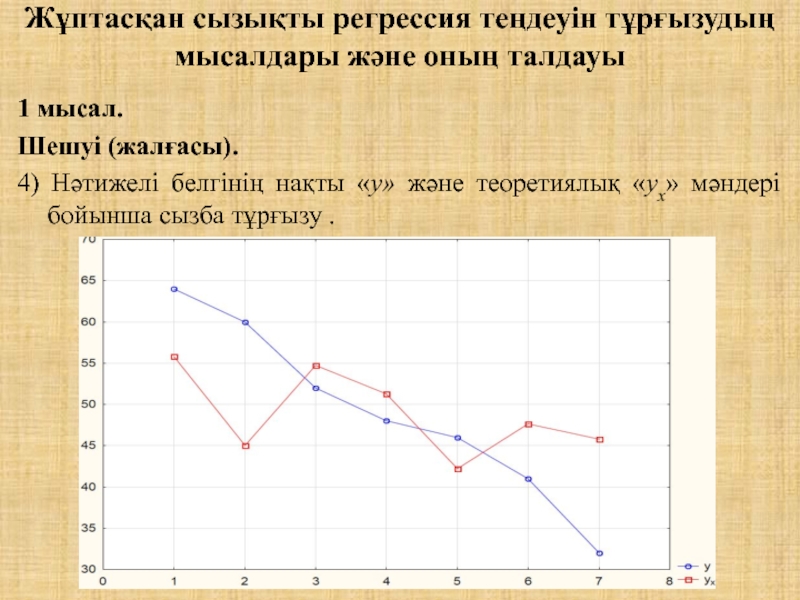
Шешуі (жалғасы).
4) Нәтижелі белгінің нақты «у» және теоретиялық «ух» мәндері
бойынша сызба тұрғызу .
Слайд 23Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы
1 мысал.
Шешуі (жалғасы).
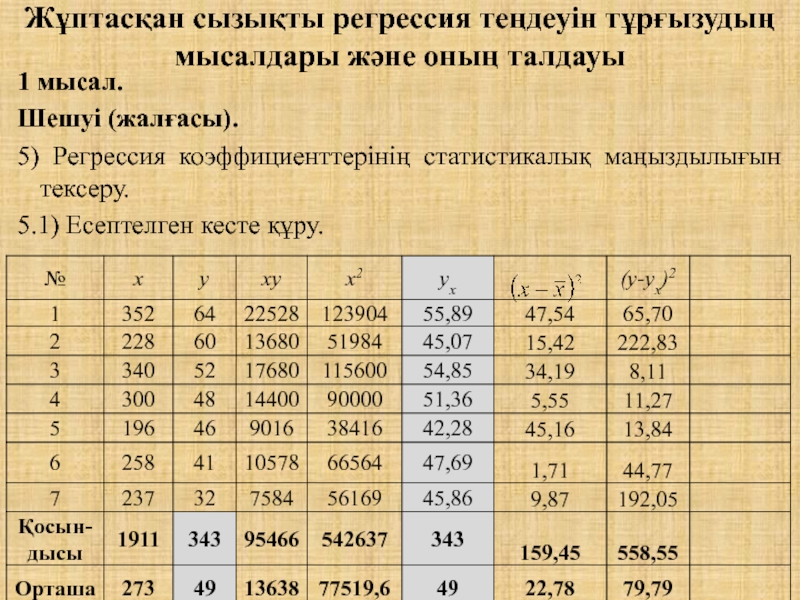
5) Регрессия коэффициенттерінің статистикалық маңыздылығын тексеру.
5.1) Есептелген кесте құру.
Слайд 24Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы
1 мысал.
Шешуі (жалғасы).
5.2) Кездейсоқ қателіктерді есептеу:
Слайд 25Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы
1 мысал.
Шешуі (жалғасы).
5.3)
5.4) tкесте(0,05; 5)=2,57.
5.5)
, яғни «b» коэффициенті – маңызды емес,
, яғни «a» коэффициенті – маңызды емес.
Слайд 26Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы
1 мысал.
Шешуі (жалғасы).
6) Регрессия теңдеуінің статистикалық маңыздылығын тексеру:
6.1)
6.2) Fкесте (р; k;
n-k-1)=(0,05; 1; 5)=6,61.
6.3) Fесеп
Слайд 27Жұптасқан сызықты регрессия теңдеуін тұрғызудың мысалдары және оның талдауы
1 мысал.
Шешуі (жалғасы).
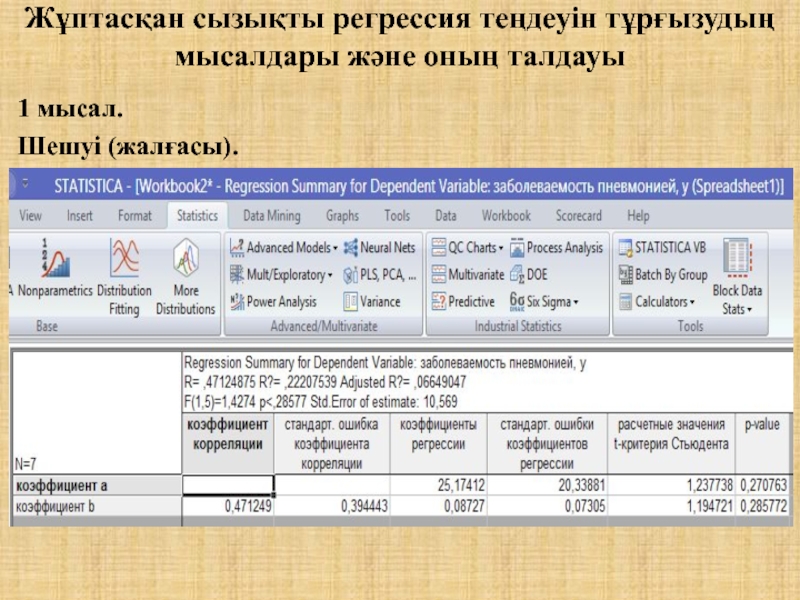
7) Детерминация коэффициентін есепте: R2=(0,47)2=0,22. Тұрғызылған теңдеу сапалы емес.
Себебі, регессиялық талдау жүргізгенде ессептеу көлемді болғандықтан, арнайы бағдарламаларды қолдану ұсынылады (Statistica 10, SPSS және т.б.)
Слайд 28Бақылау сұрақтары:
1. Регрессиялық талдау қандай кезеңдерден тұрады?
2. Регрессияның қандай
түрлерін білесіңдер?
3.Жұптасқан сызықтық регрессия теңдеуінің коэффициенттері қалай анықталады?
4. Регрессия коэффициентінің
маңыздылығы қалай тексеріледі?
5. Регрессия теңдеуінің маңыздылығы қалай тексеріледі?