Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Нечеткие знания и способы их обработки
Содержание
- 1. Нечеткие знания и способы их обработки
- 2. Лекция 6Абсолютная ясность - одна из форм полного тумана.Из фильма «Семнадцать мгновений весны»
- 3. Лекция 6При разработке интеллектуальных систем знания о
- 4. Лекция 6Даже количественные данные, полученные путем достаточно
- 5. Лекция 6Наряду с количественными характеристиками в базах
- 6. Лекция 6Разрешить это противоречие можно или путем
- 7. Лекция 6Смысл термина нечеткость многозначен, основные его компоненты следующие:недетерминированность выводов;многозначность;ненадежность;неполнота;неточность.
- 8. Лекция 6Недетерминированность выводов означает, что заранее путь
- 9. Лекция 6Ненадежность знаний и выводов. Ненадежность знаний
- 10. Лекция 6В данном подходе связи между элементами
- 11. Лекция 6Пусть Р(Н) — вероятность некоторой гипотезы
- 12. Лекция 6где P(E) - вероятность свидетельства Е,
- 13. Лекция 6Например, в экспертной системе MYSIN, предназначенной
- 14. Лекция 6В идеальном мире можно вычислить вероятность
- 15. Лекция 6Правило Байеса позволяет выполнить такие вычисления
- 16. Лекция 6В системе MYCIN применен альтернативный подход
- 17. Лекция 6ЕСЛИ пациент имеет показания и симптомы
- 18. Лекция 6Коэффициент уверенности ρ принимает значения в
- 19. Лекция 6Отличные от +1 положительные значения коэффициента
- 20. Лекция 6Основная идея состоит в том, чтобы
- 21. Лекция 6Роль фоновых знаний состоит в том,
- 22. Лекция 6Неполнота знаний и немонотонная логика. Абсолютно
- 23. Лекция 6Многие экспертные системы основаны на модели
- 24. Лекция 6Недостатки модели закрытого мира связаны с
- 25. Лекция 6Для организации логических выводов в интеллектуальных
- 26. Лекция 6Индукция (от лат. inductio выведение) процесс
- 27. Лекция 6Рассуждения, ведущие от знания о части
- 28. Лекция 6Пример: Валеев – человек, Иткис –
- 29. Лекция 6ДедукцияДедукция (от лат. deductio выведение) процесс
- 30. Лекция 6Такая последовательность мыслей называется выводом, а
- 31. Лекция 6В узком смысле слова, принятом в
- 32. Лекция 6Дедуктивное умозаключение, являющееся предметом традиционной логики,
- 33. Лекция 6Рассмотрим простейший пример абдуктивного вывода. Предположим,
- 34. Лекция 6Для того чтобы его вывести, необходимо
- 35. Лекция 6Целью абдуктивного вывода является формирование одного
- 36. Лекция 6В большинстве случаев абдуктивные гипотезы выбираются
- 37. Лекция 6Абдуктивные выводы используются в задачах диагностики
- 38. Лекция 6Характеризуя три указанных основных вида логического
- 39. Лекция 6Неточность знаний. Известно, что количественные данные
- 40. Для учета неточности лингвистических знаний используется теория
- 41. Отметим, что, идея построения нечетких множеств появилась
- 42. Теория нечетких множествразработана для оперирования с такого
- 43. Слайд 43
- 44. Слайд 44
- 45. Слайд 45
- 46. Слайд 46
- 47. Следует отметить, что первоначально теория нечетких множеств
- 48. В настоящее время теория нечетких множеств является
- 49. Развитие исследований в области нечеткий математики привело
- 50. Лекция 6Нечетким множеством А во множестве U
- 51. Лекция 6Нечеткое множество можно записать следующим образом:
- 52. Лекция 6Примеры записи нечетких множествЕсли U =
- 53. Лекция 6Обычные множества составляют подкласс класса нечетких множеств. Функцией принадлежности обычного множества является функция:
- 54. Лекция 6Носителем нечеткого множества А
- 55. Высотой h(A) нечеткого множества А называется величинаНечеткое
- 56. Лекция 6Примеры нечетких множествПусть универсальное множество U
- 57. Лекция 6Пусть U — множество людей в
- 58. Слайд 58
- 59. Лекция 6Пусть U = (-8, -5, -3,
- 60. Лекция 6Нечеткое подмножество универсального множества U может
- 61. Лекция 6А есть подмножество В или содержится
- 62. Лекция 6Множеством α-уровня нечеткого множества А является
- 63. Лекция 6Множество α-уровня называют иногда сечением α
- 64. Лекция 6Рассмотрим более подробно физический смысл функции
- 65. Лекция 6В работе Лотфи А. Заде «Fuzzy
- 66. Лекция 6В случае, когда А - некоторое
- 67. Лекция 6Методы построения функции принадлежности:Пусть имеется коллективный
- 68. Лекция 6При применении метода построения функции принадлежности
- 69. Лекция 6В методе парных соотношений пусть имеется
- 70. Лекция 6Экспертная оценка для i-го эксперта находится
- 71. Слайд 71
- 72. Слайд 72
- 73. Слайд 73
- 74. Лекция 6
- 75. Скачать презентанцию
Лекция 6Абсолютная ясность - одна из форм полного тумана.Из фильма «Семнадцать мгновений весны»
Слайды и текст этой презентации
Слайд 3Лекция 6
При разработке интеллектуальных систем знания о конкретной предметной области,
для которой создается система, редко бывают полными и абсолютно достоверными.
Слайд 4Лекция 6
Даже количественные данные, полученные путем достаточно точных экспериментов, имеют
статистические оценки достоверности, надежности, значимости и т.д. Информация, которой заполняются
экспертные системы, получается в результате опроса экспертов, мнения которых субъективны и могут расходиться.
Слайд 5Лекция 6
Наряду с количественными характеристиками в базах знаний ИИС должны
храниться качественные показатели, эвристические правила, текстовые знания и т.д. При
обработке знаний с применением жестких механизмов формальной логики возникает противоречие между нечеткими знаниями и четкими методами логического вывода.
Слайд 6Лекция 6
Разрешить это противоречие можно или путем преодоления нечеткости знаний
(когда это возможно), или с использованием специальных методов представления и
обработки нечетких знаний.
Слайд 7Лекция 6
Смысл термина нечеткость многозначен, основные его компоненты следующие:
недетерминированность выводов;
многозначность;
ненадежность;
неполнота;
неточность.
Слайд 8Лекция 6
Недетерминированность выводов означает, что заранее путь решения конкретной задачи
в пространстве ее состояний определить невозможно. Поэтому в большинстве случаев
методом проб и ошибок выбирается некоторая цепочка логических заключений, согласующихся с имеющимися знаниями, а в случае если она не приводит к успеху, организуется перебор с возвратом для поиска другой цепочки и т.д. Такой подход предполагает определение некоторого первоначального пути.
Слайд 9Лекция 6
Ненадежность знаний и выводов. Ненадежность знаний означает, что для
оценки их достоверности нельзя применить двухбалльную шкалу (1 — абсолютно
достоверные; 0 — недостоверные знания). Для более тонкой оценки достоверности знаний применяется вероятностный подход, основанный на теореме Байеса и другие методы.
Слайд 10Лекция 6
В данном подходе связи между элементами знаний не разделяются
на типы; вместо этого каждому элементарному фрагменту знаний (факту, представленному
парой атрибут — значение или утверждением) ставится в соответствие минимальное или максимальное значение байесовской вероятности, после чего степени надежности выводимых заключений рассчитываются как апостериорные (условные) вероятности по формулам, полученным на базе формулы Байеса.
Слайд 11Лекция 6
Пусть Р(Н) — вероятность некоторой гипотезы (заключения) при отсутствии
каких-либо свидетельств (т.е. априорная вероятность, назначаемая экспертом) и пусть Р(Н
: Е) — апостериорная вероятность гипотезы H при наличии свидетельства (факта) Е, вычисляемая по формуле:
Слайд 12Лекция 6
где P(E) - вероятность свидетельства Е, которая вычисляется по
формуле
Р(Е:Н) - вероятность наличия свидетельства Е при условии истинности
гипотезы H (например, вероятность наличия высокой температуры при заболевании гриппом); Р(Е :¬H) — вероятность свидетельства Е при условии ложности заключения H (вероятность высокой температуры у пациента, не болеющего гриппом) 
Слайд 13Лекция 6
Например, в экспертной системе MYSIN, предназначенной для диагностики и
выбора метода лечения инфекционных заболеваний, разработан метод вывода с использованием
коэффициентов уверенности
Слайд 14Лекция 6
В идеальном мире можно вычислить вероятность P(di| E), где
di — i-я диагностическая категория, а E представляет все необходимые
дополнительные свидетельства или фундаментальные знания, используя только вероятности P(di|Sj), где Sj является j-м клиническим наблюдением (симптомом).
Слайд 15Лекция 6
Правило Байеса позволяет выполнить такие вычисления только в том
случае, если, во-первых, доступны все значения P(dj|Si), и, во-вторых, правдоподобно
предположение о взаимной независимости симптомов.
Слайд 16Лекция 6
В системе MYCIN применен альтернативный подход на основе правил
влияния, которые следующим образом связывают имеющиеся данные (свидетельства) с гипотезой
решения:
Слайд 17Лекция 6
ЕСЛИ пациент имеет показания и симптомы s1,..., sk и
имеют место определенные фоновые условия t1…tm ,
ТО можно с
уверенностью ρ заключить, что пациент страдает заболеванием di.
Слайд 18Лекция 6
Коэффициент уверенности ρ принимает значения в диапазоне [-1,+ 1].
Если ρ = +1, то это означает, что при соблюдении
всех оговоренных условий составитель правила абсолютно уверен в правильности заключения di, а если ρ = -1, то значит, что при соблюдении всех оговоренных условий существует абсолютная уверенность в ошибочности этого заключения.![Лекция 6Коэффициент уверенности ρ принимает значения в диапазоне [-1,+ 1]. Если ρ = +1, то это означает,](/img/thumbs/c180c34a4078bb927bee767e2a50f472-800x.jpg "Нечеткие знания и способы их обработки Лекция 6Коэффициент уверенности ρ принимает значения в диапазоне [-1,+ 1]. Если")
Слайд 19Лекция 6
Отличные от +1 положительные значения коэффициента указывают на степень
уверенности в правильности заключения di, а отрицательные значения — на
степень уверенности в его ошибочности.
Слайд 20Лекция 6
Основная идея состоит в том, чтобы с помощью порождающих
правил такого вида попытаться заменить вычисление P(di | s1 ...sk)
приближенной оценкой и таким образом сымитировать процесс принятия решения экспертом-человеком.
Слайд 21Лекция 6
Роль фоновых знаний состоит в том, чтобы разрешить или
запретить применение правила в данном конкретном случае. Пусть, например, имеется
диагностическое правило, связывающее появление болей в брюшной полости с возможной беременностью. Применение этого правила блокируется фоновым знанием, что оно справедливо только по отношению к пациентам-женщинам.
Слайд 22Лекция 6
Неполнота знаний и немонотонная логика. Абсолютно полных знаний не
бывает, поскольку процесс познания бесконечен. В связи с этим состояние
базы знаний должно изменяться с течением времени. В отличие от простого добавления информации, как в базах данных, при добавлении новых знаний возникает опасность получения противоречивых выводов, т.е. выводы, полученные с использованием новых знаний, могут опровергать те, что были получены ранее.
Слайд 23Лекция 6
Многие экспертные системы основаны на модели закрытого мира, обусловленной
применением аппарата формальной логики для обработки знаний. Модель закрытого мира
предполагает жесткий отбор знаний, включаемых в базу, а именно: БЗ заполняется исключительно верными понятиями, а все, что ненадежно или неопределенно, заведомо считается ложным. Другими словами, все, что известно базе знаний, является истиной, а остальное — ложью.
Слайд 24Лекция 6
Недостатки модели закрытого мира связаны с тем, что формальная
логика исходит из предпосылки, согласно которой набор определенных в системе
аксиом (знаний) является полным (теория является полной, если каждый ее факт можно доказать, исходя из аксиом этой теории). Для полного набора знаний справедливость ранее полученных выводов не нарушается с добавлением новых фактов. Это свойство логических выводов называется монотонностью. Реальные знания, закладываемые в экспертные системы, крайне редко бывают полными.
Слайд 25Лекция 6
Для организации логических выводов в интеллектуальных системах с неполными
знаниями вместо традиционных дедукции и индукции применяется абдукция .
Слайд 26Лекция 6
Индукция (от лат. inductio выведение) процесс логического вывода на
основании перехода от частных положений к общим. Среди наиболее важных
законов индуктивной логики выступают правила доказательства, связывающие причину и следствие: всегда, когда возникает причина, возникает и феномен (следствие); всегда, когда есть феномен (следствие).
Слайд 27Лекция 6
Рассуждения, ведущие от знания о части предметов (частного знания)
к знанию обо всех предметах определенного класса (общему знанию), —
это типичные индукции. Всегда остается вероятность того, что обобщение окажется поспешным и необоснованным.
Слайд 28Лекция 6
Пример: Валеев – человек, Иткис – человек, Антонов –
человек, Немцов – человек.
Валеев – студент АС – 663, Иткис
- студент АС – 663, Антонов - студент АС – 663, Немцов - студент АС – 663.Значит все люди студенты. Все студенты АС –663 –люди.
Слайд 29Лекция 6
Дедукция
Дедукция (от лат. deductio выведение) процесс логического вывода на
основании перехода от общих положений к частным.Дедукция - в широком
смысле слова - такая форма мышления, когда новая мысль выводится чисто логическим путем (т.е. по законам логики) из предшествующих мыслей.
Слайд 30Лекция 6
Такая последовательность мыслей называется выводом, а каждый компонент этого
вывода является либо ранее доказанной мыслью, либо аксиомой, либо гипотезой.
Последняя мысль данного вывода называется заключением.Процессы дедукции на строгом уровне описываются в исчислениях математической логики.
Слайд 31Лекция 6
В узком смысле слова, принятом в традиционной логике, под
термином “дедукция” понимают дедуктивное умозаключение, т. е. такое умозаключение, в
результате которого получается новое знание о предмете или группе предметов на основании уже имеющегося некоторого знания об исследуемых предметах и применения к ним некоторого правила логики.
Слайд 32Лекция 6
Дедуктивное умозаключение, являющееся предметом традиционной логики, применяется нами всякий
раз, когда требуется рассмотреть какое - либо явление на основании
уже известного нам общего положения и вывести в отношении этого явления необходимое заключение.Пример: Если Кабалдин отличник, то он получит красный диплом. Кабалдин не получил красный диплом. Значит он не отличник.
Слайд 33Лекция 6
Рассмотрим простейший пример абдуктивного вывода. Предположим, теория содержит правило:
«ЕСЛИ студент отлично знает математику, ТО он может стать хорошим
инженером» и факт: «Студент Иванов отлично знает математику». Кроме того, имеется наблюдение: «Студент Иванов стал хорошим экономистом», которое не выводится из заданной теории.
Слайд 34Лекция 6
Для того чтобы его вывести, необходимо сформировать абдуктивную (объясняющую)
гипотезу, которая не будет противоречить вышеприведенной теории. Такой гипотезой может
быть, например, следующая: «Хороший математик может стать хорошим экономистом».
Слайд 35Лекция 6
Целью абдуктивного вывода является формирование одного (или более) объяснения
∆ наблюдаемого факта G на основе информации, хранящейся в БЗ
интеллектуальной системы (теория T). Объяснение А должно быть таким, чтобыT υ ∆├ G и чтобы T υ ∆ было непротиворечиво.
Наблюдение G можно вывести из теории T лишь при ее расширении некоторым множеством гипотез А.
Слайд 36Лекция 6
В большинстве случаев абдуктивные гипотезы выбираются из заранее определенного
множества предложений, обращающих определенный аспект знаний конкретной предметной области.
Слайд 37Лекция 6
Абдуктивные выводы используются в задачах диагностики для обнаружения причин
наблюдаемого неправильного поведения систем, в задачах, связанных с пониманием естественного
языка, для решения проблем накопления и усвоения знаний и т.д.
Слайд 38Лекция 6
Характеризуя три указанных основных вида логического выведения умозаключений, Ч.
Пирс писал: "Дедукция доказывает, что нечто должно быть, индукция показывает,
что нечто действительно в настоящий момент, абдукция всего лишь предполагает, что нечто может быть".
Слайд 39Лекция 6
Неточность знаний.
Известно, что количественные данные (знания) могут быть
неточными, при этом существуют количественные оценки такой неточности Доверительный интервал,
уровень значимости, степень адекватности и т.д.). Лингвистические знания также могут быть неточными.
Слайд 40Для учета неточности лингвистических знаний используется теория нечетких множеств, предложенная
Л. Заде в 1965 г. Этому ученому принадлежат слова: «Фактически
нечеткость может быть ключом к пониманию способности человека справляться с задачами, которые слишком сложны для решения на ЭВМ».
Слайд 41Отметим, что, идея построения нечетких множеств появилась в связи с
исследованием известного античного «парадокса кучи» в трудах Е. Бореля еще
в 1959 г., т. е. за 15 лет до Л. А. Заде. Однако, именно благодаря Л. А. Заде теория приобрела математически формализованный вид.До появления аппарата теории нечетких множеств любая неопределенность, появляющаяся при решении практических задач, отождествлялась со случайностью. В то же время в повседневной жизни мы часто используем такие понятия, как большой, малый, хороший, простой, сложный, горячий и т. д., которые являются нечеткими, расплывчатыми, однако эта неопределенность не носит вероятностного характера.
Слайд 42Теория нечетких множеств
разработана для оперирования с такого рода объектами. Случайность
всегда связана с
неопределенностью, касающейся принадлежности некоторого объекта к вполне четкому
множеству.
Понятие же нечеткости относится к классам, в которых имеются различныеградации степени принадлежности, промежуточные между полной принадлежностью и не
принадлежностью объектов к данному классу. Иными словами, нечеткое множество есть
класс объектов, в котором нет резкой границы между теми объектами, которые входят в этот
класс, и теми, которые в него не входят.
Слайд 47Следует отметить, что первоначально теория нечетких множеств была откровенно негативно
оценена научной общественностью. Наиболее критически воспринималась явная направленность теории на
оперирование с субъективными неопределенностями. В конце 60- х годов работы Л. Заде даже были рассмотрены в Конгрессе США как яркий пример бессмысленной траты государственных средств, выделяемых на развитие науки .
Слайд 48В настоящее время теория нечетких множеств является развитым научным направлением,
имеющим большое прикладное значение. Она широко применяется в решении технических
проблем. На ее основе получены решения большого числа задач анализа и управления энергетическими системами , технологическими процессами и установками: химическими реакторами, электрическими двигателями , процессами сварки , установками для очищения воды , холодильными агрегатами, вентиляторами и кондиционерами , нагревательными приборами и др.
Слайд 49
Развитие исследований в области нечеткий математики привело к появлению нечеткой
логики и нечетких выводов, которые выполняются с использованием знаний, представленных
нечеткими множествами, нечеткими отношениями, нечеткими соответствиями и т. д.
Слайд 50Лекция 6
Нечетким множеством А во множестве U называется совокупность пар
вида
(u, μA(u)),
где ,
а μA(u)) –
это функция принадлежности нечеткого множества А, μA(u)): U→ [0,1]. Здесь U- некоторое обычное множество, называемое универсальным множеством.
Слайд 52Лекция 6
Примеры записи нечетких множеств
Если U = (a, b, с,
d, e, f); М = (0, 0.5, 1), тогда А
можно представить в виде: А = (0/а, 1/b, 0.5/c, 0/d, 0.5/e, 0/f).Если А = (0.8/a1, 1/а2, 0.4/аз, 0.2/а4, 0.5/а5, 0/а6), то U = (a1, a2, аз, a4, а5,a6); М=(0, 0.2, 0.4, 0.5, 0.8, 1).
Слайд 53Лекция 6
Обычные множества составляют подкласс класса нечетких множеств. Функцией принадлежности
обычного множества является функция:
Слайд 54Лекция 6
Носителем нечеткого множества А называется
обычное подмножество таких точек U, для которых величина μA(u)),
положительна.Носитель обозначается S(A) или SuppA:
Слайд 55Высотой h(A) нечеткого множества А называется величина
Нечеткое множество А называется
нормальным, если его высота равна единице. В противном случае нечеткое
множество А субнормально.Субнормальное нечеткое множество всегда можно нормализовать, поделив функцию принадлежности μA(u)на величину h(A).
Элементы множества U, для которых степень принадлежности μA(u) = 0.5 называются точками перехода нечеткого множества.
Слайд 56Лекция 6
Примеры нечетких множеств
Пусть универсальное множество U представлено в виде
(а, Ь, с, d, e) и нечеткое подмножество А, заданное
на U, имеет вид А = (0/а, 0.5/b, 0.6/c, 0.7/d, 0.85/е).Тогда носителем нечеткого множества А является S(A) = (b, с, d, e). Высота нечеткого множества А - h(A)=0.85. Точка перехода u=b. Множество А - субнормально. Нормализованное множество будет иметь вид:
А = (0/а, 0.6/b, 0.7/c, 0.8/d, 1/е).
Слайд 57Лекция 6
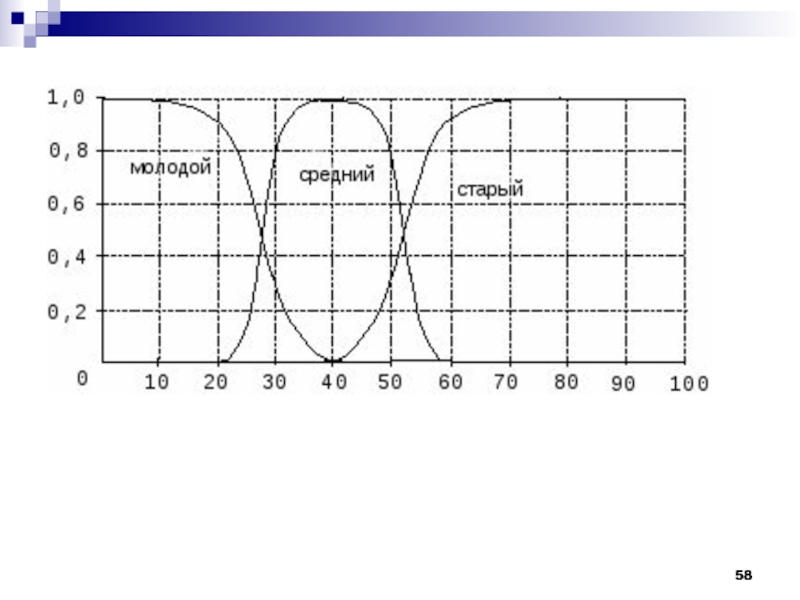
Пусть U — множество людей в возрасте от 0
до 100 лет и пусть понятия «молодой», «среднего возраста» и
«старый» представлены нечеткими множествами F1, F2 и F3 соответственно. Эти нечеткие множества являются подмножествами множества U. Функции принадлежности элементов множества U к понятиям, представленным нечеткими множествами F1,F2,F3 имеют следующий вид:
Слайд 59Лекция 6
Пусть U = (-8, -5, -3, 0, 1,2, 4,
6, 9) - множество целых чисел. Тогда нечеткое подмножество чисел,
по абсолютной величине близких к нулю, можно определить, например, так:А = (0/-8, 0.5/-5, 0.7/-3, 1/0, 0.9/1, 0.8/2, 0.6/4, 0.4/6, 0/9)
Слайд 60Лекция 6
Нечеткое подмножество универсального множества U может быть подмножеством другого
нечеткого или обычного подмножества (то есть с функцией принадлежности, принимающей
значения 0 или 1) множества A.
Слайд 61Лекция 6
А есть подмножество В или содержится в В тогда
и только тогда, когда μa(u) < μb(u) для любого и
множества U.Пример
Если универсальное множество U = (а, Ь, с, d), определенные на нем нечеткие подмножества А и В равны соответственно А = (0.5/а, 0.8/b, 0.3/d), В = (0.7/а, 1/b, 0.3/с, 1/d), то
Слайд 62Лекция 6
Множеством α-уровня нечеткого множества А является обычное множество Аα
всех таких элементов универсального множества U, степень принадлежности которых нечеткому
множеству А больше или равна α :
Слайд 63Лекция 6
Множество α-уровня называют иногда сечением α нечеткого множества А.
Причем, если µA(u) > α , то говорят о сильном
сечении, если µA(u) ≥ α , то о слабом сечении.Пример
Если нечеткое множество А = {0.3/а, 0.4/d, 0.7/c, 0.8/f, 0.6/b}, то множеством α -уровня при α =0.7 будет множество А 0.7 = {с, f}.
Слайд 64Лекция 6
Рассмотрим более подробно физический смысл функции принадлежности. Спектр мнений
по этому вопросу чрезвычайно широк. Так, например, очень часто на
функцию принадлежности накладывается условие нормировки, тем самым, выбирая в качестве функции принадлежности плотность распределения вероятности.
Слайд 65Лекция 6
В работе Лотфи А. Заде «Fuzzy sets» предполагается, что
функция принадлежности - это некоторое "невероятностное субъективное измерение неточности", и
что она отлична от плотности вероятности и от функции распределения вероятности. Иногда под функцией принадлежности понимают возможность или полезность того или иного события.
Слайд 66Лекция 6
В случае, когда А - некоторое понятие естественного языка,
a U -множество объектов, обозначаемых этим понятием A, µa(u) -
есть вероятность того, что лицо, принимающее решение, использует А в качестве имени объекта. Такая интерпретация функции принадлежности называется вероятностной и не исключает существование других интерпретаций.
Слайд 67Лекция 6
Методы построения функции принадлежности:
Пусть имеется коллективный ЛПР, состоящий из
n экспертов. О том, что и е U принадлежит нечеткому
множеству А, n1(n1 ≤ n) экспертов отвечают положительно. В этом случаеμa(u)=n1/n
Данный метод называется частотным, а сама схема вычисления соответствует вероятностной интерпретации функции принадлежности.
Слайд 68Лекция 6
При применении метода построения функции принадлежности на основе стандартного
набора графиков ЛПР выбирает наиболее подходящий, по его мнению, график
из стандартного набора, а затем в диалоговом режиме с ЭВМ выясняет и корректирует (при необходимости) параметры выбранного графика.
Слайд 69Лекция 6
В методе парных соотношений пусть имеется n экспертов и
необходимо найти степени принадлежности k точек. Каждый i-ый эксперт должен
определить парные соотношения (по своему усмотрению) типа:
Слайд 70Лекция 6
Экспертная оценка для i-го эксперта находится по формуле
Окончательно,
функция принадлежности для i-го параметра имеет вид
