Слайд 1Нейронные вычислительные сети
Слайд 2Теория нейронных сетей: предмет
Хорошо известно, что человеческий
мозг по своим возможностям далеко превосходит обычные компьютеры при решении
многих задач. Кроме того, мозг обладает еще целым рядом особенностей, которые ставят его вне конкуренции по сравнению с современными компьютерами, а также с лучшими приборами, созданными человеком. Это следующие особенности, которые были выработаны биологическими нейронными сетями в процессе биологической эволюции в течении 600 млн. лет:
надежность и устойчивость к повреждениям;
способность к адаптации и обучению;
способность иметь дело с неполной, избыточной, зашумленной информацией;
высокая степень параллельности при функционировании;
очень низкие энергетические затраты.
При этом все процессы обработки информации выполняются биологическими системами автоматически, без какого-либо напряжения сознания или специального управления.
Мозг – высоко распараллеленная система, в которой информация передается в виде пространственно-временных
структур нервного возбуждения. Это значительно более гибкий и эффективный способ обработки информации, чем тот, который используется в современных традиционных компьютерах (несмотря на то, что скорость работы нейронов в раз меньше, чем скорость работы транзисторов).
Способность к обучению – адаптации к условиям и возможностям в изменяющейся внешней среде – столь важная особенность нейронных сетей, что теперь присоединена в качестве отдельного пункта к так называемому «тесту Тьюринга», являющемуся операционным определением понятия интеллект.
Основные цели исследований в области теории нейронных сетей – выяснение принципов работы мозга, а также изучение общих возможностей систем, осуществляющих параллельную распределенную обработку информации. Основное средство – построение и изучение моделей искусственных нейронных сетей.
Одна из основных целей – создание нейрокомпьютеров.

Слайд 3Cтроение биологического нейрона
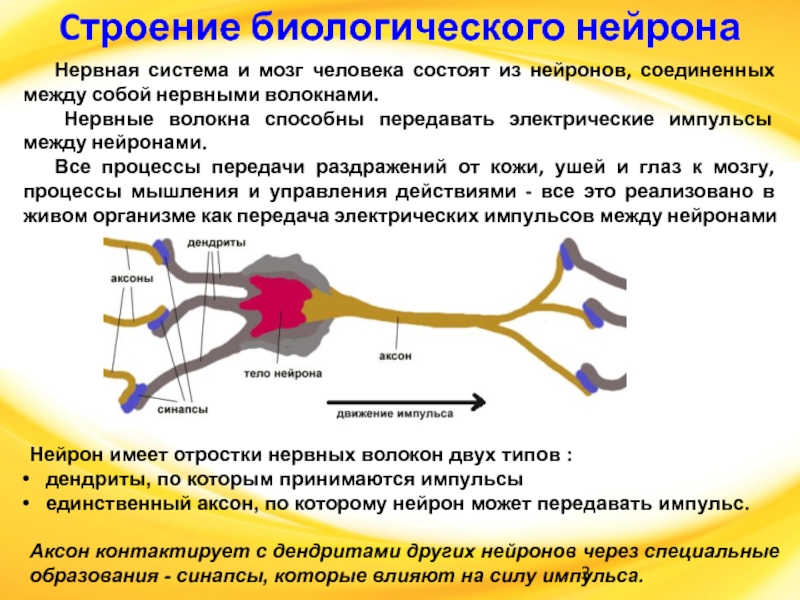
Нервная система и мозг человека состоят из нейронов,
соединенных между собой нервными волокнами.
Нервные волокна способны передавать электрические
импульсы между нейронами.
Все процессы передачи раздражений от кожи, ушей и глаз к мозгу, процессы мышления и управления действиями - все это реализовано в живом организме как передача электрических импульсов между нейронами
Нейрон имеет отростки нервных волокон двух типов :
дендриты, по которым принимаются импульсы
единственный аксон, по которому нейрон может передавать импульс.
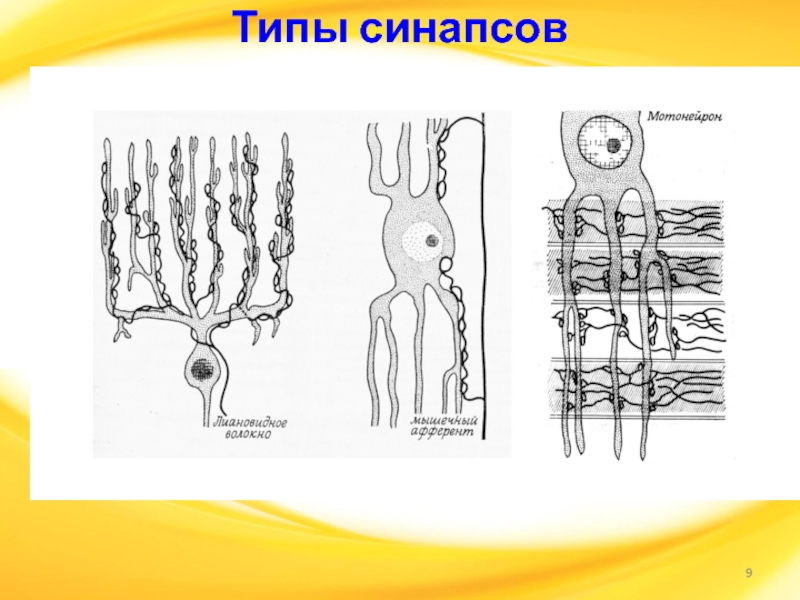
Аксон контактирует с дендритами других нейронов через специальные образования - синапсы, которые влияют на силу импульса.
Слайд 4Биологический прототип: нейронные структуры мозга
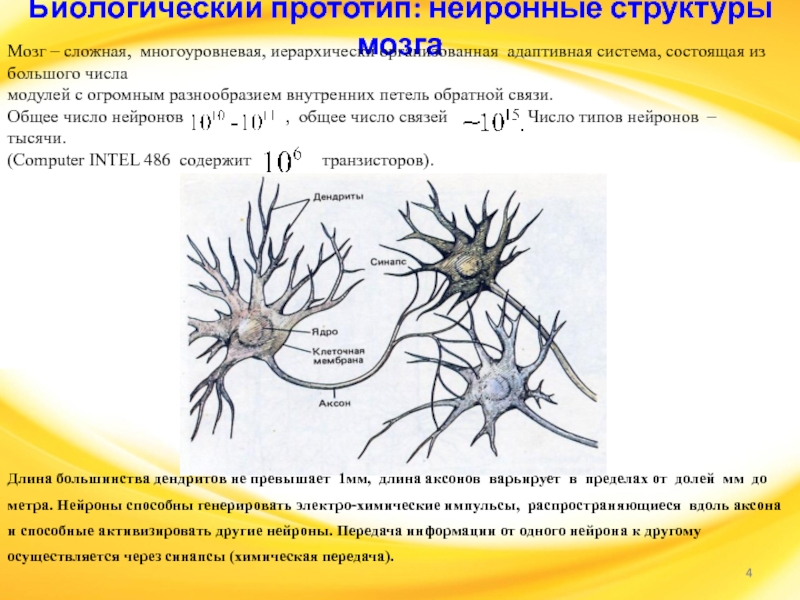
Мозг – сложная,
многоуровневая, иерархически организованная адаптивная система, состоящая из большого числа
модулей с
огромным разнообразием внутренних петель обратной связи.
Общее число нейронов , общее число связей Число типов нейронов – тысячи.
(Сomputer INTEL 486 содержит транзисторов).
Длина большинства дендритов не превышает 1мм, длина аксонов варьирует в пределах от долей мм до метра. Нейроны способны генерировать электро-химические импульсы, распространяющиеся вдоль аксона и способные активизировать другие нейроны. Передача информации от одного нейрона к другому осуществляется через синапсы (химическая передача).
Слайд 5Нейроны мозга
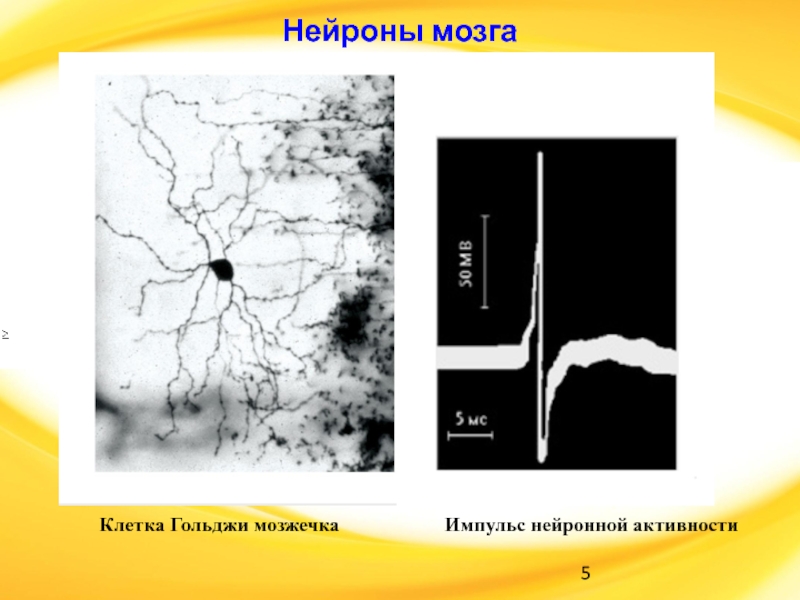
Клетка Гольджи мозжечка
Импульс нейронной активности
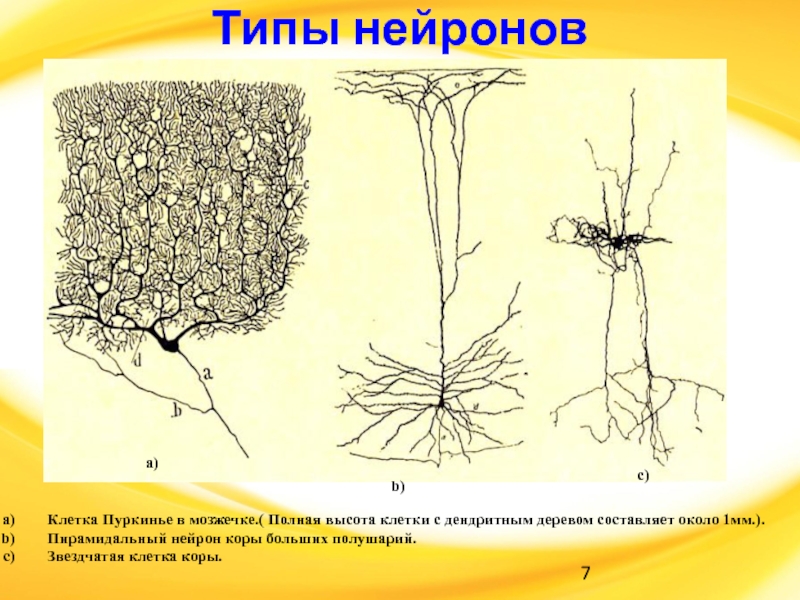
Слайд 7Типы нейронов
a)
b)
c)
Клетка Пуркинье в мозжечке.( Полная высота клетки с
дендритным деревом составляет около 1мм.).
Пирамидальный нейрон коры больших полушарий.
Звездчатая клетка
коры.
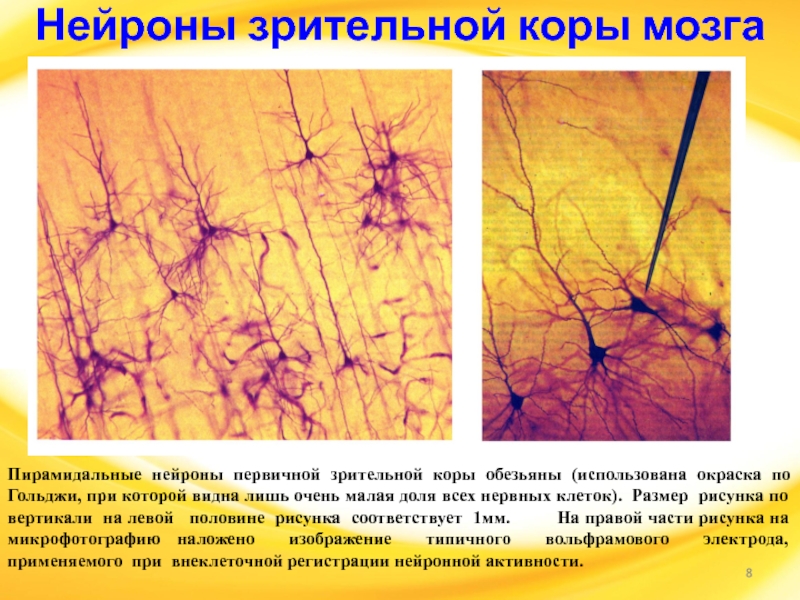
Слайд 8Нейроны зрительной коры мозга
Пирамидальные нейроны первичной зрительной коры
обезьяны (использована окраска по Гольджи, при которой видна лишь очень
малая доля всех нервных клеток). Размер рисунка по вертикали на левой половине рисунка соответствует 1мм. На правой части рисунка на микрофотографию наложено изображение типичного вольфрамового электрода, применяемого при внеклеточной регистрации нейронной активности.
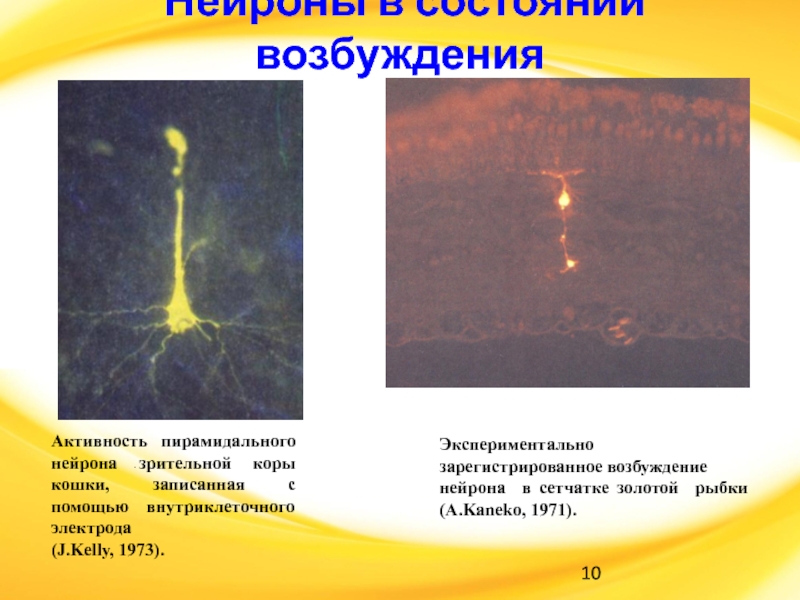
Слайд 10 Нейроны в состоянии возбуждения
.
Активность пирамидального нейрона зрительной коры
кошки, записанная с помощью внутриклеточного электрода
(J.Kelly, 1973).
Экспериментально зарегистрированное возбуждение
нейрона
в сетчатке золотой рыбки (A.Kaneko, 1971).
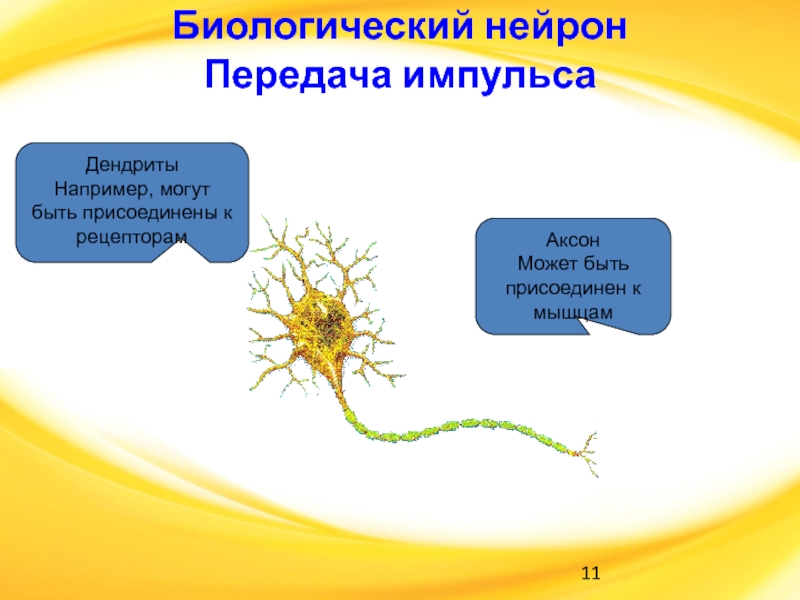
Слайд 11Биологический нейрон
Передача импульса
Дендриты
Например, могут быть присоединены к рецепторам
Аксон
Может быть присоединен
к мышцам
Слайд 12Биологические нейронные сети
1872-1895 гг.
Понятие нейрона и нейронной сети;
Первые предположения о
принципе работы;
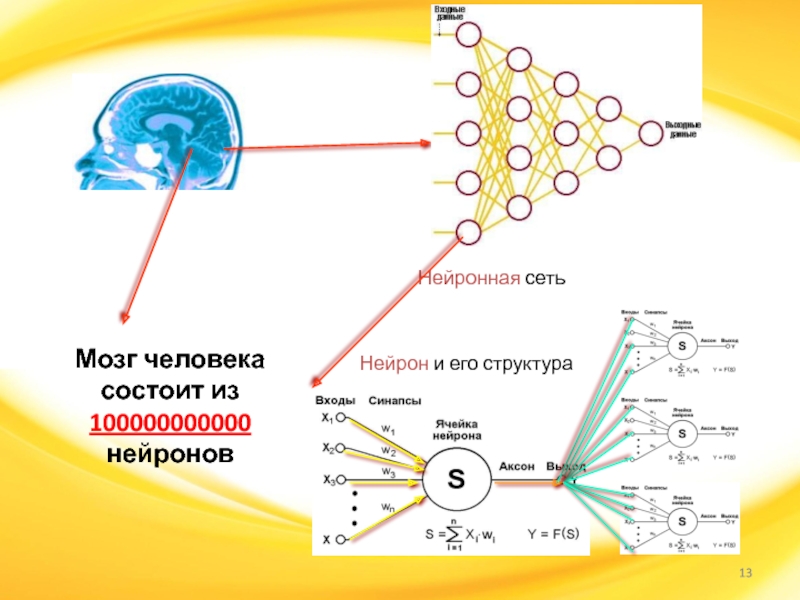
Нейронная сеть
Нейрон и его структура
Мозг человека
состоит из
100000000000
нейронов
Слайд 14Нейронная сеть
Совокупность соединенных между собой нейронов;
Сеть осуществляет преобразование входного сигнала
с рецепторов в выходной, являющейся реакцией организма на внешнюю среду
Слайд 15Нейровычислительная архитектура
Для повышения производительности ЭВМ необходимо перейти от принципов фон-Неймана
к параллельной обработке информации. Тем не менее, параллельные компьютеры пока
не получили распространения по нескольким причинам
Одним из вариантов реализации классов архитектур вычислительных систем является нейрокомпьютер.
Нейрокомпьютер - это вычислительная система с MIMD архитектурой, которая представляет собой совокупность очень простых однотипных процессорных элементов (нейронов), объединенных множественными связями.
Основные преимущества нейрокомпьютеров связаны с массовым параллелизмом обработки, который обуславливает высокое быстродействие при низких требованиях к параметрам элементарных узлов. Устойчивые и надёжные нейросистемы могут создаваться из низконадёжных элементов, имеющих большой разброс параметров
Любой нейрокомпьютер по своему строению представляет нейронную сеть (нейросеть). Нейронная сеть - это сеть с конечным числом слоёв, состоящих из однотипных элементов - аналогов нейронов с различными типами связи между слоями.
Элементарным строительным элементом нейронной сети (НС) является нейрон, который осуществляет взвешенное суммирование поступающих на его вход сигналов. Результат такого суммирования образует промежуточный выходной сигнал, который преобразуется активационной функцией в выходной сигнал нейрона.

Слайд 16Нейронные сети
Предпосылка:
Известно, что биологические системы (люди, животные) прекрасно справляются со
сложными задачами распознавания образов;
Основная идея:
Применить знания о работе мозга (людей,
животных) для решения задач распознавания образов;
Слайд 17Искусственные нейронные сети
Искусственная нейронная сеть – массивный
параллельный распределенный процессор, в котором заложены возможности для хранения и
воспроизведения информации, и который имеет сходство с мозгом в двух отношениях:
1) информация приобретается посредством процесса обучения;
2) хранение информации является распределенным и осуществляется в форме распределения связей между элементами сети.
(S.Haykin, 1994)
Сеть состоит из большого числа простых активных элементов, каждый из которых оперирует только локальной информацией. Вся сеть осуществляет параллельную обработку информации.
Термин «нейронная» отражает тот факт, что объект возник под влиянием представления о биологических нейронных сетях.
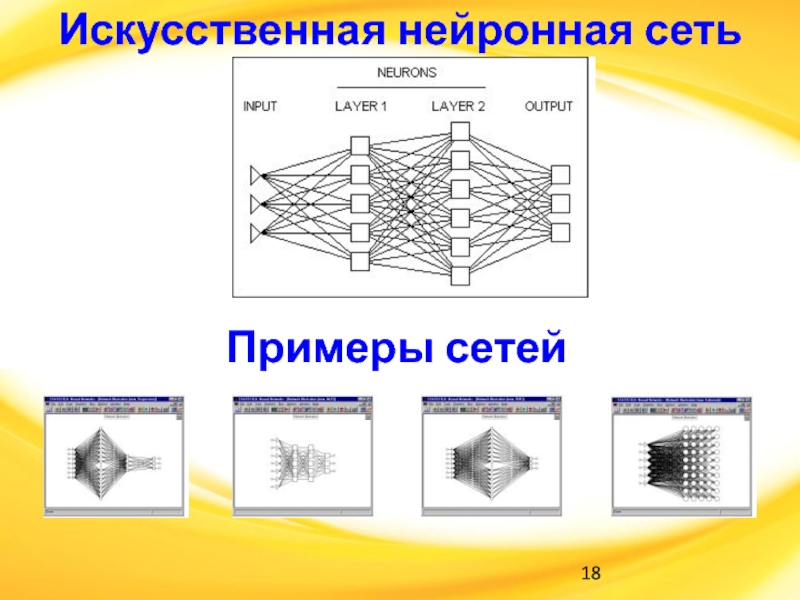
Слайд 18Примеры сетей
Искусственная нейронная сеть
Слайд 20Области применения
Распознавание образов
Оценка кредитного риска
Прогнозирование финансовых
потоков и объемов продаж
Маркетинговые исследования
Медицинская
диагностика
Автоматизированные
системы управления
“Добыча данных”
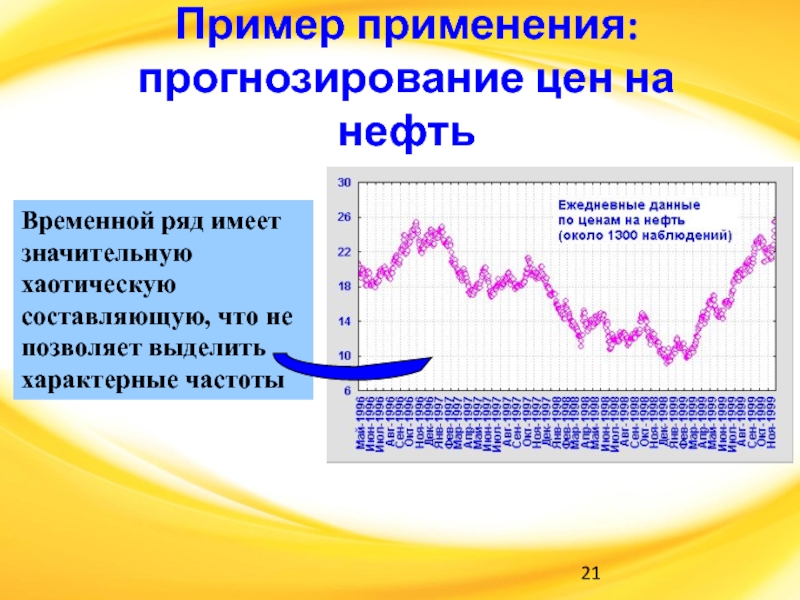
Слайд 21Пример применения:
прогнозирование цен на нефть
Временной ряд имеет значительную хаотическую составляющую,
что не позволяет выделить характерные частоты
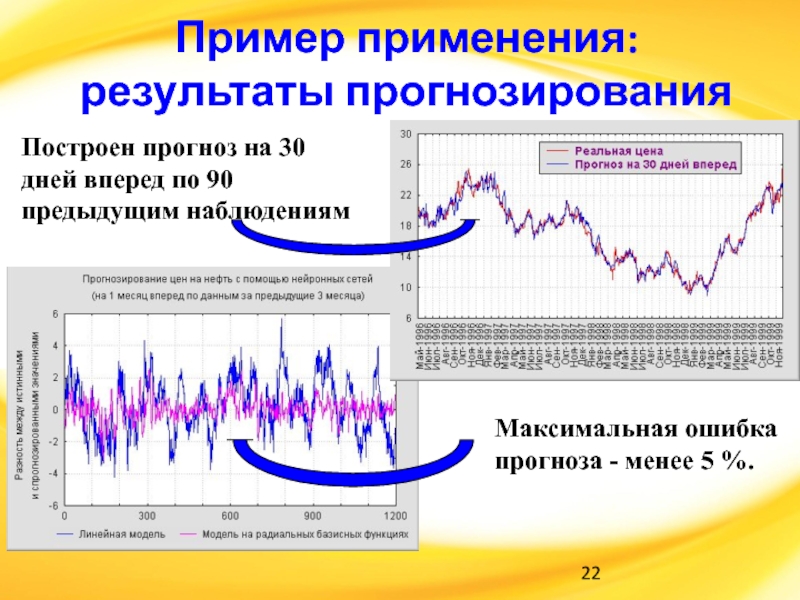
Слайд 22Пример применения:
результаты прогнозирования
Построен прогноз на 30 дней вперед по 90
предыдущим наблюдениям
Максимальная ошибка прогноза - менее 5 %.
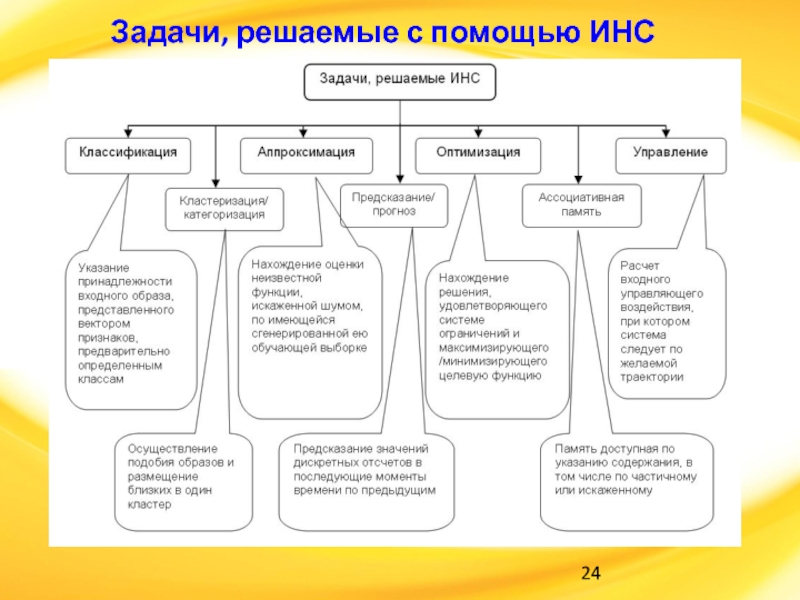
Слайд 23Решаемые задачи
Задачи, успешно решаемые НС на данном этапе их развития:
формирование
моделей и различных нелинейных и трудно описываемых математически систем, прогнозирование
развития этих систем во времени:
системы управления и регулирования с предсказанием; управление роботами, другими сложными устройствами
разнообразные конечные автоматы: системы массового обслуживания и коммутации, телекоммуникационные системы;
распознавание зрительных, слуховых образов;
ассоциативный поиск информации и создание ассоциативных моделей; синтез речи; формирование естественного языка;
принятие решений и диагностика в областях, где отсутствуют четкие математические модели: в медицине, криминалистике, финансовой сфере;
Слайд 25Преимущества нейронных сетей
Предлагают стандартные способы решения многих нестандартных задач.
Явное описание
модели заменяется созданием «образовательной среды».
Приводят к успеху там, где отказывают
традиционные методы и трудно создать явный алгоритм:
анализ данных со сложной нелинейной структурой зависимостей;
задачи распознавания и классификации;
нелинейное понижение размерности.
Слайд 26Преимущества нейронных сетей
Кроме этого, применение НС обеспечивает следующие полезные свойства:
1.
Способность к обобщению. Под термином обобщение понимается способность НС устанавливать
концентрацию вредных веществ на основе данных, не встречающихся в процессе обучения.
2. Нелинейность. НС, построенная из соединений нелинейных нейронов, является нелинейной. Нелинейность является чрезвычайно важным свойством, поскольку входной сигнал, подаваемый в НС, в случае определения количественного состава вещества, представляет собой спектр поглощения ИК излучения веществом и является нелинейным.
3. Отображение входной информации в выходную. Наиболее часто используется для обучения НС парадигма обучения с учителем. Настройка синаптических весов сети происходит на основе набора учебных примеров. Каждый пример состоит из параметров входного сигнала и соответствующего ему желаемого отклика. Из этого множества случайным образом выбирается пример, а НС модифицирует синаптические веса для минимизации расхождений желаемого выходного сигнала и формируемого сетью согласно выбранному статистическому критерию. Обучение проводится до тех пор, пока изменения синаптических весов не станут незначительными.
4. Адаптивность. Нейронные сети обладают способностью адаптировать свои синаптические веса к изменениям входных сигналов. В частности, нейронные сети, обученные действовать с определенными сигналами, могут быть легко переучены для работы в условиях незначительных колебаний параметров.
5. Эксплуатация обученной нейронной сети не требует дополнительной подготовки пользователей и их высокой квалификации.
Кроме этого, нейросетевой метод моделирования не требует априорного задания вида исследуемой зависимости.

Слайд 27Структура и свойства искусственного нейрона
Нейрон состоит из элементов трех типов:
умножителей (синапсов), сумматора и нелинейного преобразователя. Синапсы осуществляют связь между
нейронами, умножают входной сигнал на число, характеризующее силу связи, (вес синапса). Сумматор выполняет сложение сигналов, поступающих по синаптическим связям от других нейронов, и внешних входных сигналов. Нелинейный преобразователь реализует нелинейную функцию одного аргумента - выхода сумматора. Эта функция называется функцией активации или передаточной функцией нейрона.
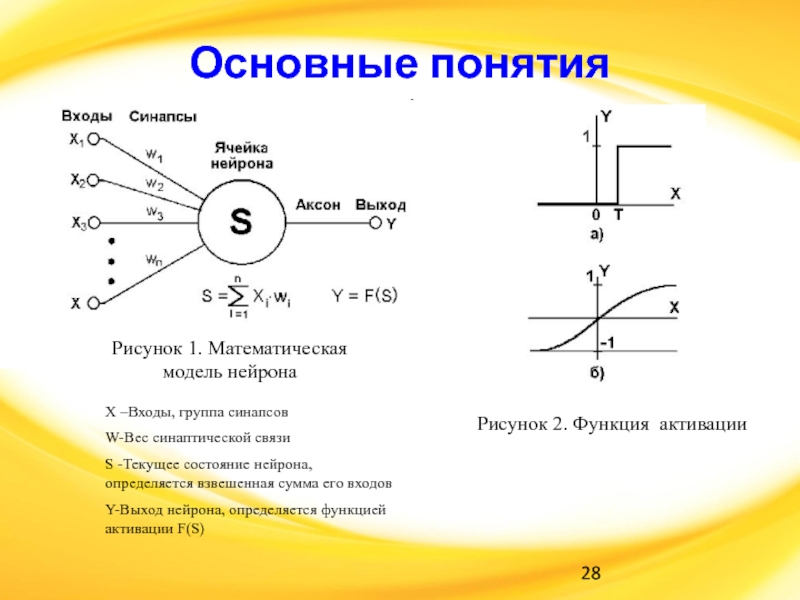
Слайд 28Основные понятия
Рисунок 1. Математическая модель нейрона
X –Входы, группа синапсов
W-Вес синаптической
связи
S -Текущее состояние нейрона, определяется взвешенная сумма его входов
Y-Выход нейрона,
определяется функцией активации F(S)
Рисунок 2. Функция активации
Слайд 30Математическая модель нейрона
Синапсы дендритов имеют веса w1, w2, w3.
К синапсам поступают импульсы силы x1, x2, x3
После
прохождения синапсов и дендритов к нейрону поступают импульсы :
w1x1,
w2x2,
w3x3.
Нейрон преобразует полученный суммарный импульс x=w1x1+ w2x2+ w3x3 в соответствии с некоторой передаточной функцией f(x)
Сила выходного импульса равна y=f(x)=f(w1x1+ w2x2+ w3x3).
Нейрон полностью описывается своими весами wk и передаточной функцией f(x).
Получив набор чисел (вектор) xk в качестве входов, нейрон выдает некоторое число y на выходе.
модель нейрона с тремя входами (дендритами)\
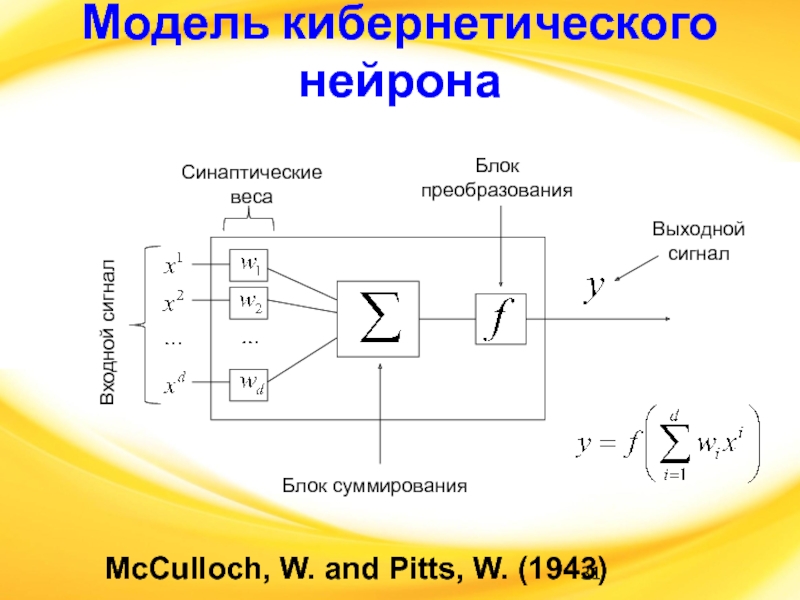
Слайд 31Модель кибернетического нейрона
McCulloch, W. and Pitts, W. (1943)
Входной сигнал
Синаптические
веса
Блок
суммирования
Блок
преобразования
Выходной
сигнал
Слайд 32Формальный нейрон МакКаллока и Питтса
.
Модель не учитывает
многих особенностей работы реальных нейронов ( импульсного характера активности, нелинейности
суммирования входной информации, рефрактерности ). Тем не менее она была плодотворно использована во многих моделях сетей.
Здесь t - дискретное время,
H (x) – функция активации
– порог
Если , то H(x) – функция Хевисайда
при и
при
Если
то
Значения отвечают возбуждающим синапсам, значения – тормозным.
Нейрон возбужден при Тогда
Нейрон может находиться в двух состояниях.
Слайд 33Структура и свойства искусственного нейрона
Нейрон реализует скалярную функцию векторного аргумента
Математическая
модель нейрона:
y = f(s)
где wi, - вес синапса, i =
1...n; b - значение смещения; s - результат суммирования; xi - компонент входного вектора (входной сигнал), i = 1...n;
у - выходной сигнал нейрона; n - число входов нейрона; f - нелинейное преобразование (функция активации).
В общем случае входной сигнал, весовые коэффициенты и смещение могут принимать действительные значения. Выход (у) определяется видом функции активации и может быть как действительным, так и целым.
Синаптические связи с положительными весами называют возбуждающими, с отрицательными весами – тормозящими.
Описанный вычислительный элемент можно считать упрощенной математической моделью биологических нейронов
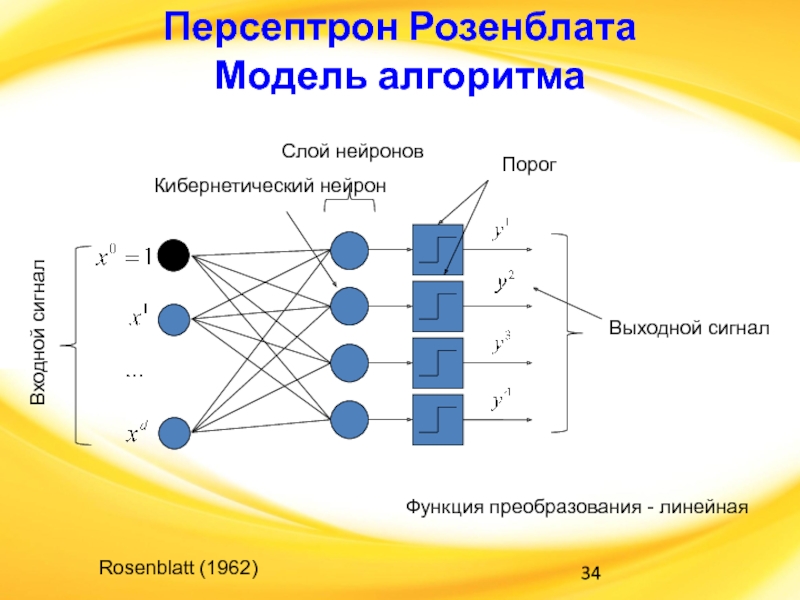
Слайд 34Персептрон Розенблата
Модель алгоритма
Входной сигнал
Слой нейронов
Функция преобразования - линейная
Порог
Выходной сигнал
Кибернетический нейрон
Rosenblatt
(1962)
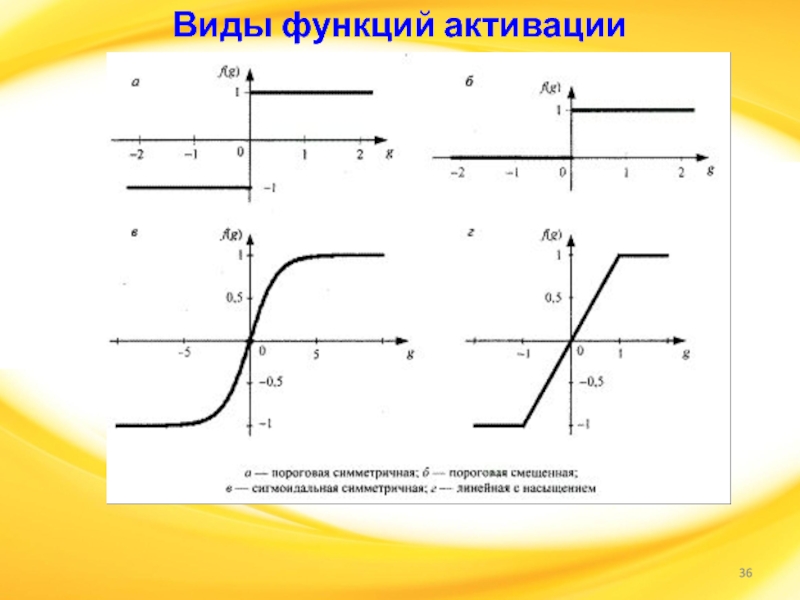
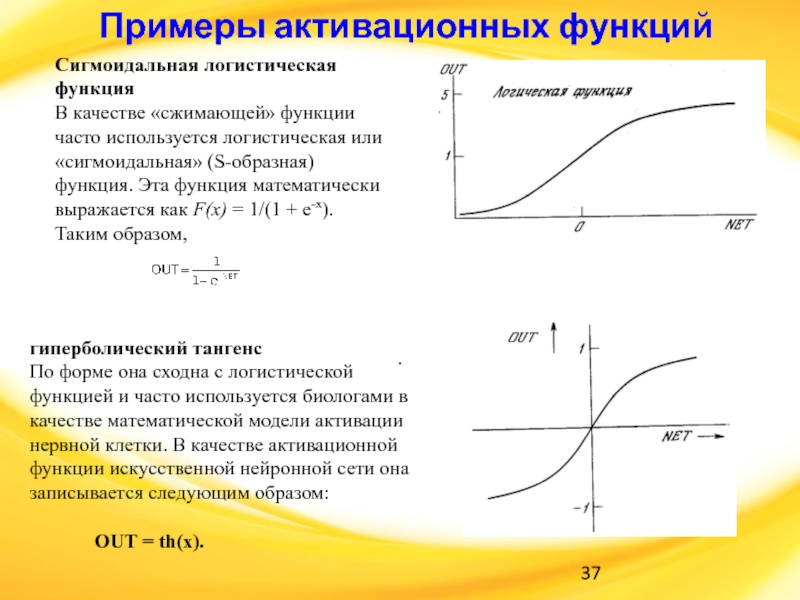
Слайд 37Примеры активационных функций
Сигмоидальная логистическая функция
В качестве «сжимающей» функции часто
используется логистическая или «сигмоидальная» (S-образная) функция. Эта функция математически выражается
как F(x) = 1/(1 + е-x). Таким образом,
.
гиперболический тангенс
По форме она сходна с логистической функцией и часто используется биологами в качестве математической модели активации нервной клетки. В качестве активационной функции искусственной нейронной сети она записывается следующим образом:
OUT = th(x).
Слайд 38Синтез нейронных сетей
В зависимости от функций, выполняемых нейронами в сети,
можно выделить три типа нейронов:
• входные нейроны, на которые подается
вектор, кодирующий входное воздействие или образ внешней среды; в них обычно не осуществляется вычислительных процедур, а информация передается с входа на выход путем изменения их активации;
• выходные нейроны, выходные значения которых представляют выходы нейронной сети; преобразования в них осуществляются по выражениям (1.1) и (1.2);
• промежуточные нейроны, составляющие основу нейронных сетей, преобразования в которых выполняются также по выражениям (1.1) и (1.2).
В большинстве нейронных моделей тип нейрона связан с его расположением в сети. Если нейрон имеет только выходные связи, то это входной нейрон, если наоборот - выходной нейрон. В процессе функционирования сети осуществляется преобразование входного вектора в выходной, некоторая переработка информации.
Известные нейронные сети можно разделить по типам структур нейронов на гомогенные (однородные) и гетерогенные. Гомогенные сети состоят из нейронов одного типа с единой функцией активации, а в гетерогенную сеть входят нейроны с различными функциями активации.

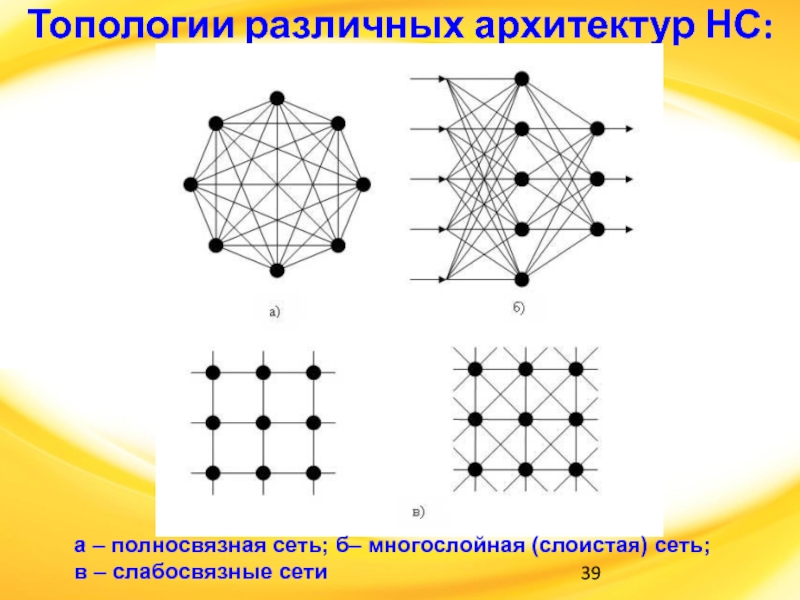
Слайд 39Топологии различных архитектур НС:
а – полносвязная сеть; б– многослойная (слоистая)
сеть;
в – слабосвязные сети
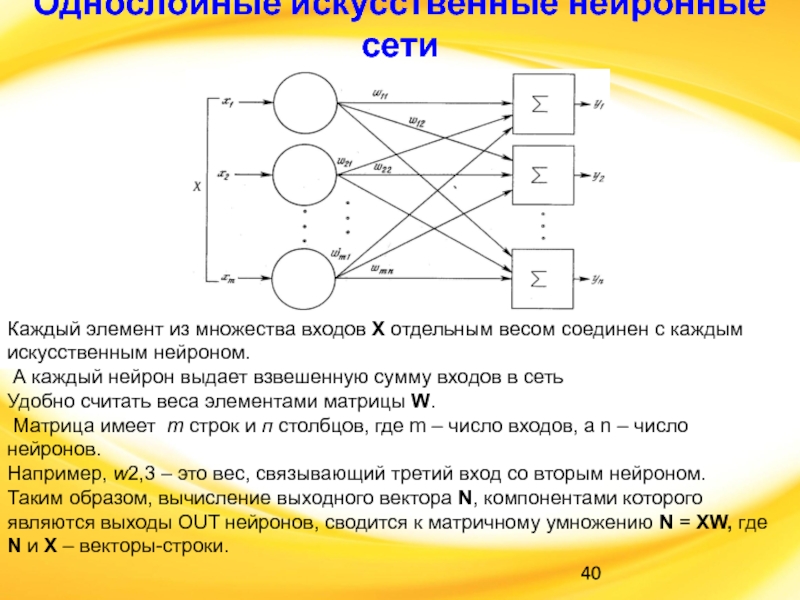
Слайд 40Однослойные искусственные нейронные сети
Каждый элемент из множества входов Х отдельным
весом соединен с каждым искусственным нейроном.
А каждый нейрон выдает
взвешенную сумму входов в сеть
Удобно считать веса элементами матрицы W.
Матрица имеет m строк и п столбцов, где m – число входов, а n – число нейронов.
Например, w2,3 – это вес, связывающий третий вход со вторым нейроном.
Таким образом, вычисление выходного вектора N, компонентами которого являются выходы OUT нейронов, сводится к матричному умножению N = XW, где N и Х – векторы-строки.
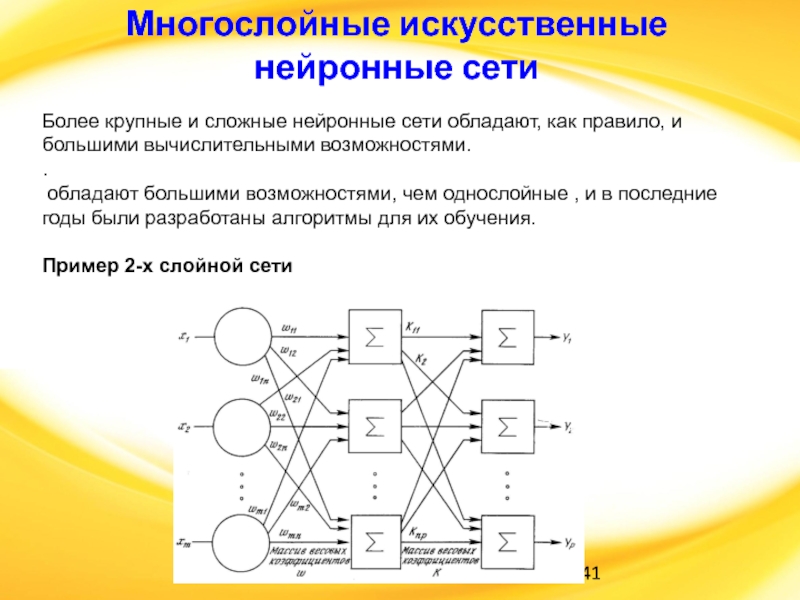
Слайд 41Многослойные искусственные нейронные сети
Более крупные и сложные нейронные сети обладают,
как правило, и большими вычислительными возможностями.
.
обладают большими возможностями,
чем однослойные , и в последние годы были разработаны алгоритмы для их обучения.
Пример 2-х слойной сети
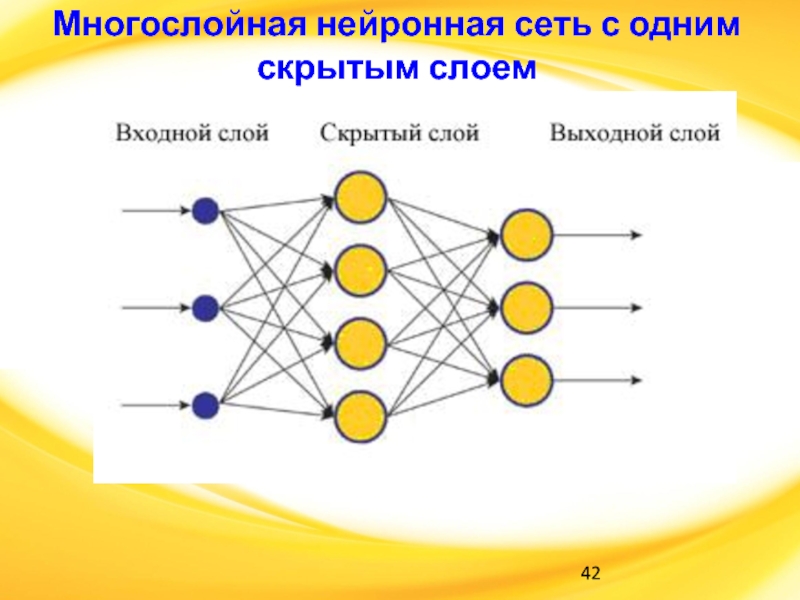
Слайд 42Многослойная нейронная сеть с одним скрытым слоем
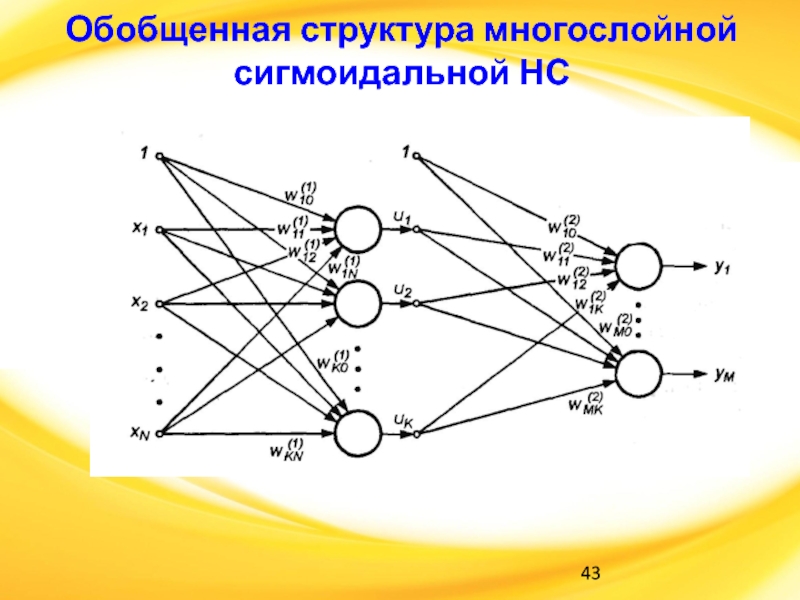
Слайд 43Обобщенная структура многослойной сигмоидальной НС
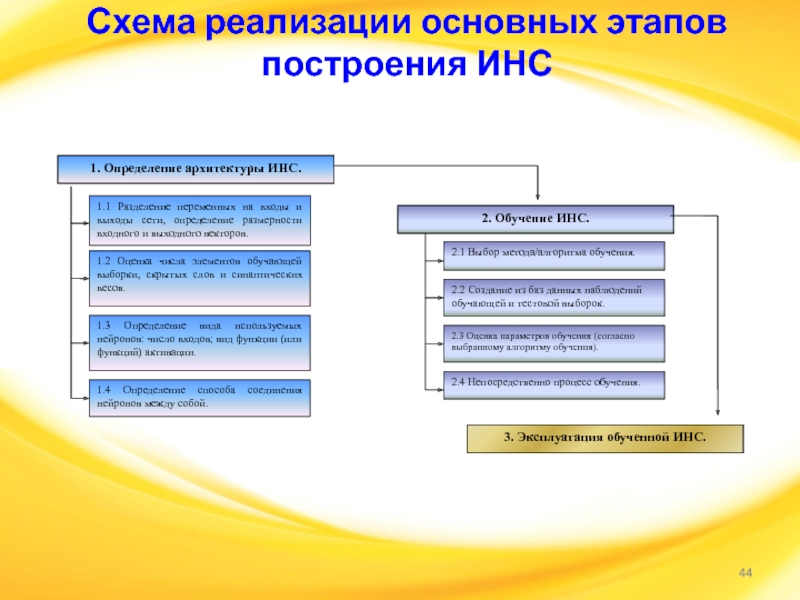
Слайд 44Схема реализации основных этапов построения ИНС
Слайд 45Как построить нейронную сеть
2 этапа:
Выбор типа (архитектуры) нейронной сети.
какие нейроны мы хотим использовать (число входов, передаточные
функции);
каким образом следует соединить их между собой;
что взять в качестве входов и выходов нейронной сети.
2. Подбор весов (обучение) нейронной сети.
.
"обучить" выбранную нейронную сеть - подобрать такие значения ее весов, чтобы она работала нужным образом. Необученная нейронная сеть подобна ребенку - ее можно научить чему угодно.
Наиболее популярный из этих алгоритмов - метод обратного распространения ошибки (Error Back Propagation), используемый, например, для обучения перцептрона.
Слайд 46Выбор количества нейронов и слоев
Количество нейронов и слоев связано:
1) со
сложностью задачи;
2) с количеством данных для обучения;
3) с требуемым количеством
входов и выходов сети;
4) с имеющимися ресурсами: памятью и быстродействием машины, на которой моделируется сеть;
Если в сети слишком мало нейронов или слоев:
1) сеть не обучится и ошибка при работе сети останется большой;
2) на выходе сети не будут передаваться резкие колебания аппроксимируемой функции y(x).
Если нейронов или слоев слишком много:
1) быстродействие будет низким, а памяти потребуется много на фон-неймановских ЭВМ;
2) сеть переобучится: выходной вектор будет передавать незначительные и несущественные детали в изучаемой зависимости y(x), например, шум или ошибочные данные;
3) зависимость выхода от входа окажется резко нелинейной: выходной вектор будет существенно и непредсказуемо меняться при малом изменении входного вектора x;
4) сеть будет неспособна к обобщению: в области, где нет или мало известных точек функции y(x) выходной вектор будет случаен и непредсказуем, не будет адекватен решамой задаче
Слайд 47Подготовка входных и выходных данных
Данные, подаваемые на вход сети и
снимаемые с выхода, должны быть правильно подготовлены.
Один из распространенных способов
- масштабирование:
x = (x’ – m)⋅ c
где x - исходный вектор, x’ - масштабированный. Вектор m - усредненное значение совокупности входных данных, с - масштабный коэффициент.
Масштабирование желательно, чтобы привести данные в допустимый диапазон. Если этого не сделать, то возможно несколько проблем:
1) нейроны входного слоя или окажутся в постоянном насыщении (|m| велик, дисперсия входных данных мала) или будут все время заторможены (|m| мал, дисперсия мала);
2) весовые коэффициенты примут очень большие или очень малые значения при обучении (в зависимости от дисперсии), и, как следствие, растянется процесс обучения и снизится точность
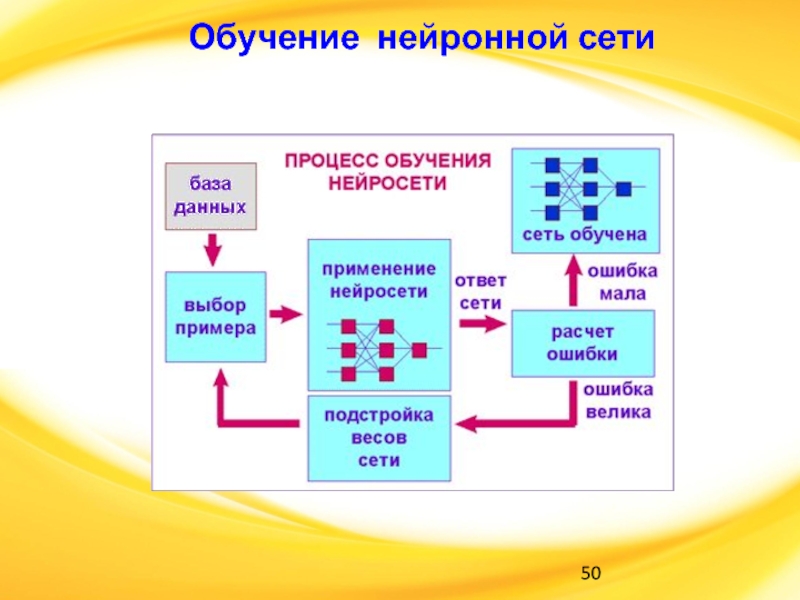
Слайд 48Обучение сети
Процесс функционирования НС зависит от величин синаптических связей, поэтому,
задавшись определенной структурой НС, отвечающей какой-либо задаче, разработчик сети должен
найти оптимальные значения всех переменных весовых коэффициентов (некоторые синаптические связи могут быть постоянными).
Этот этап называется обучением НС. Способность сети решать поставленные перед ней проблемы во время эксплуатации зависит от того, насколько качественно он будет выполнен. На этапе обучения кроме параметра качества подбора весов важную роль играет время обучения. Как правило, эти два параметра связаны обратной зависимостью и их приходится выбирать на основе компромисса.
Обучение НС может вестись с учителем или без него.
В первом случае сети предъявляются значения как входных, так и желательных выходных сигналов, и она по некоторому внутреннему алгоритму подстраивает веса своих синаптических связей.
Во втором случае выходы НС формируются самостоятельно, а веса изменяются по алгоритму, учитывающему только входные и производные от них сигналы.
Слайд 49Обучение сети
Алгоритмы обучения делятся на два больших класса: детерминистские и
стохастические. В первом из них подстройка весов представляет собой жесткую
последовательность действий, во втором – она производится на основе действий, подчиняющихся некоторому случайному процессу.
Рассмотрим алгоритм обучения с учителем.
1. Проинициализировать элементы весовой матрицы (обычно небольшими случайными значениями).
2. Подать на входы один из входных векторов, которые сеть должна научиться различать, и вычислить ее выход.
3. Если выход правильный, перейти на шаг 4.
Иначе вычислить разницу между идеальным и полученным значениями выхода:
Модифицировать веса в соответствии с определенной формулой
4. Цикл с шага 2, пока сеть не перестанет ошибаться.
На втором шаге на разных итерациях поочередно в случайном порядке предъявляются все возможные входные вектора. К сожалению, нельзя заранее определить число итераций, которые потребуется выполнить, а в некоторых случаях и гарантировать полный успех.
Слайд 51Обучение сети–метод “обратное распространение ошибки”
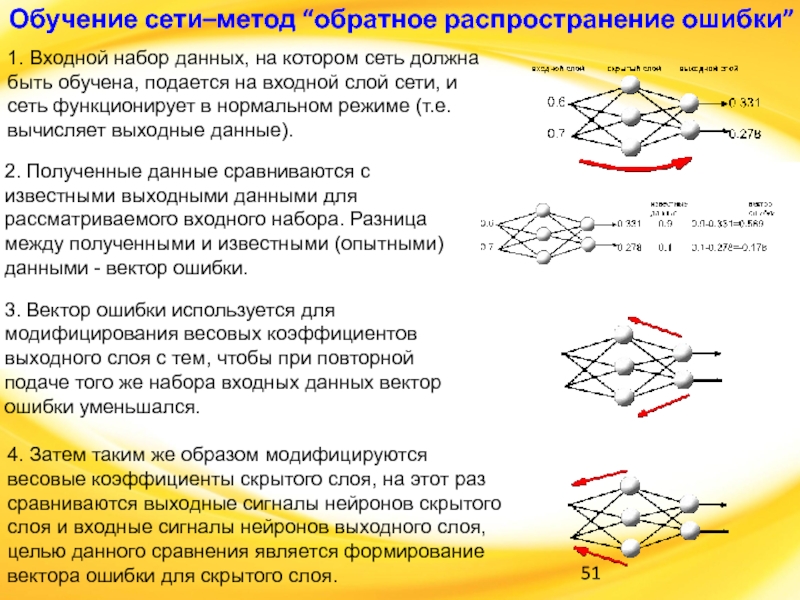
1. Входной набор данных, на котором
сеть должна быть обучена, подается на входной слой сети, и
сеть функционирует в нормальном режиме (т.е. вычисляет выходные данные).
2. Полученные данные сравниваются с известными выходными данными для рассматриваемого входного набора. Разница между полученными и известными (опытными) данными - вектор ошибки.
3. Вектор ошибки используется для модифицирования весовых коэффициентов выходного слоя с тем, чтобы при повторной подаче того же набора входных данных вектор ошибки уменьшался.
4. Затем таким же образом модифицируются весовые коэффициенты скрытого слоя, на этот раз сравниваются выходные сигналы нейронов скрытого слоя и входные сигналы нейронов выходного слоя, целью данного сравнения является формирование вектора ошибки для скрытого слоя.
Слайд 52Рекомендуемая литература
Круглов В.В., Борисов В.В. «Искусственные нейронные сети. Теория и
практика». – М.: Горячая линия – Телеком, 2001.
Хайкин С. Нейронные
сети: полный курс, 2-е изд.: Пер. с анг. ⎯ М.: ООО» И.Д. Вильямс», 2006 Осовский С. Нейронные сети для обработки информации. / Пер. с польского И.Д. Рудинского. ⎯ М.: Финансы и статистика, 2004.
Головко В.А. Нейронные сети: обучение, организация и применение. Кн. 4: учебное пособие для вузов. – М.: ИПРЖР, 2001. – 256 с.
В.В. Круглов, М.И. Дли, Р.Ю. Голунов. Нечеткая логика и искусственные нейронные сети.
Барский А.Б. Нейронные сети: распознавание, управление, принятие решений. – М. Финансы и статистика, 2004.
Каллан Роберт. Основные концепции нейронных сетей.: Пер. с англ. –М.:Издательский дом «Вильямс», 2003.