Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ МНОЖЕСТВ
Содержание
- 1. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ МНОЖЕСТВ
- 2. Ключевые словамножествопустое множествопересечение двух множествобъединение двух множеств дополнение множествамощность множества формула включений-исключений
- 3. Понятие множестваМножество — совокупность объектов произвольной природы, которая рассматривается как единое целое.!
- 4. Способы задания множестваКакие множества можно задавать перечислением всех элементов? ?
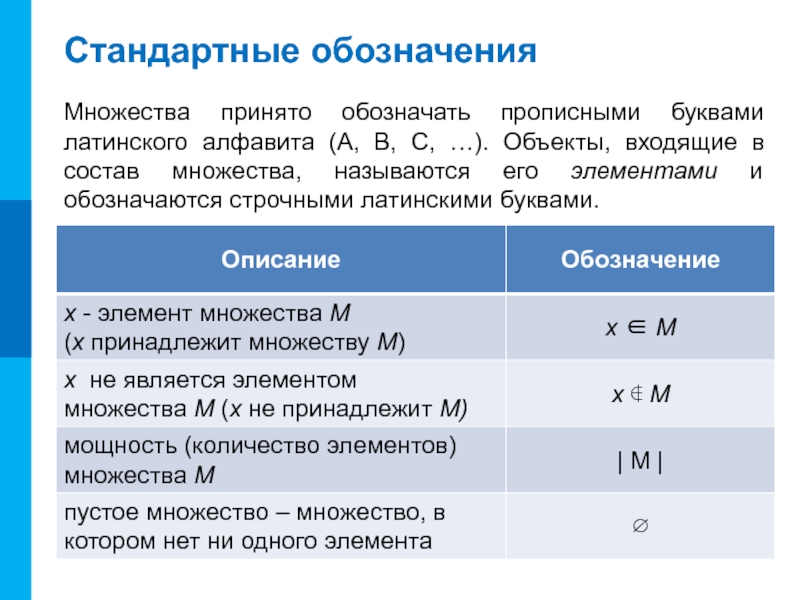
- 5. Стандартные обозначенияМножества принято обозначать прописными буквами латинского
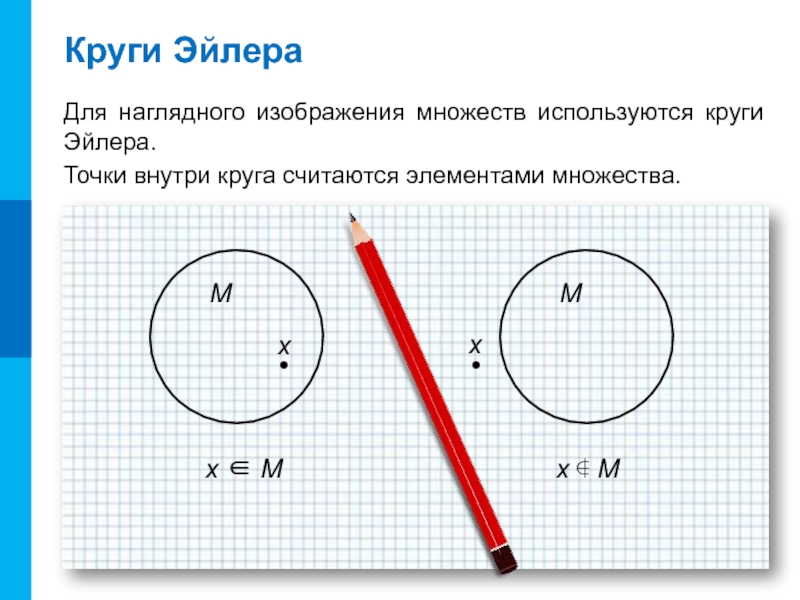
- 6. Круги ЭйлераДля наглядного изображения множеств используются круги
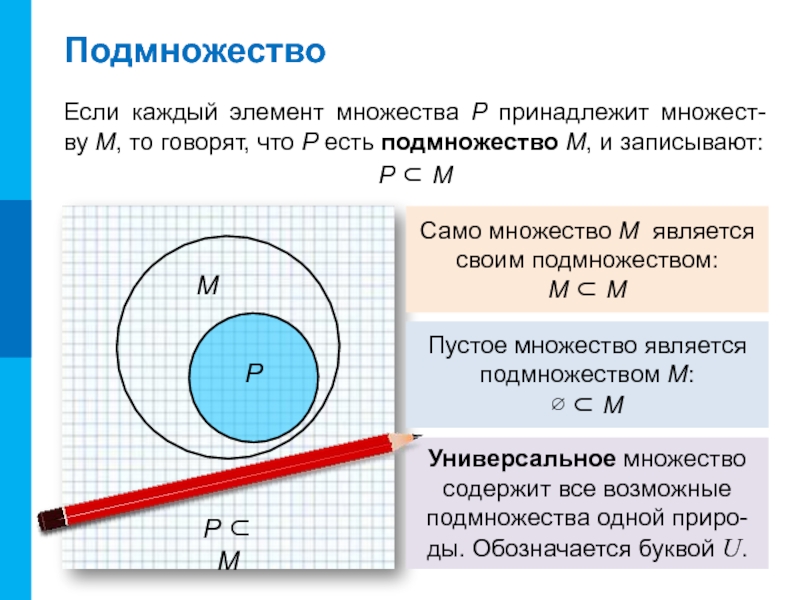
- 7. ПодмножествоЕсли каждый элемент множества P принадлежит множест-
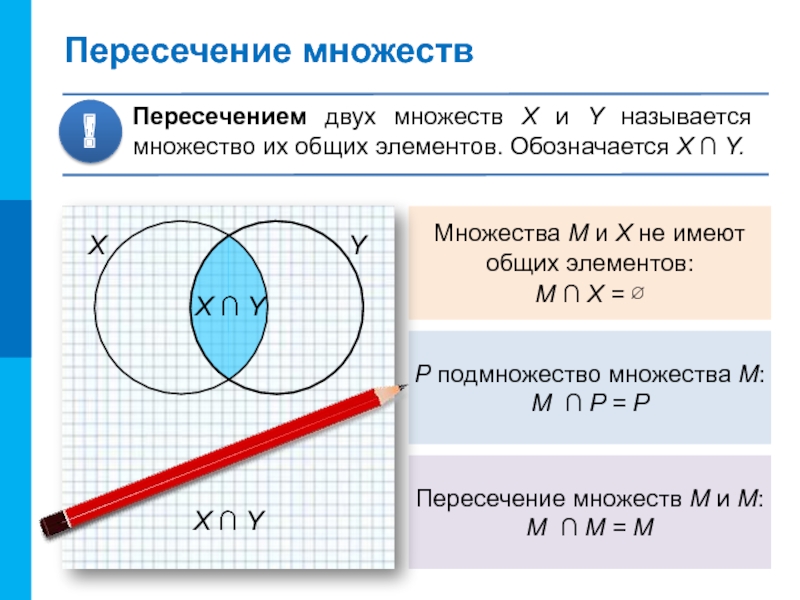
- 8. Множества M и X не имеют общих
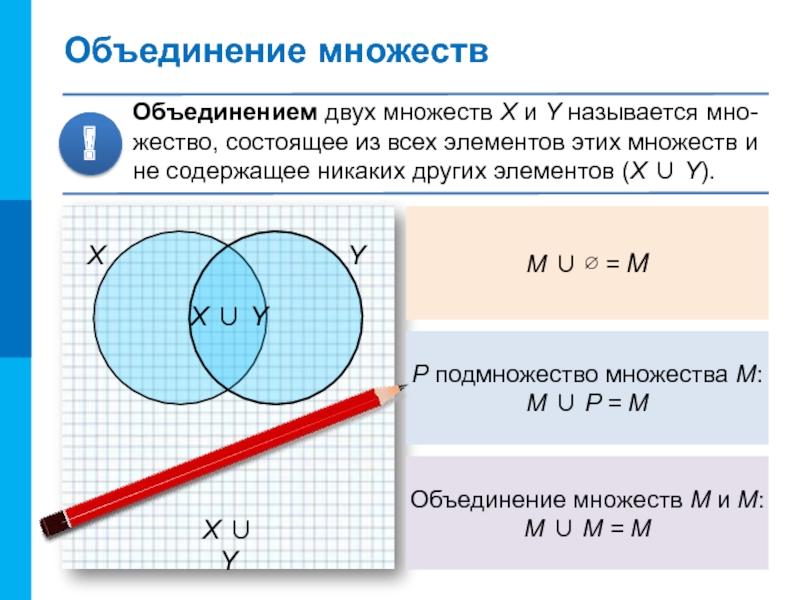
- 9. X ∪ YОбъединение множествОбъединением двух множеств X
- 10. Примеры пересечения и объединения множествXYX ∪ Y
- 11. Дополнение множестваПусть множество P является подмножеством множества
- 12. Мощность множестваМощностью конечного множества называется число его
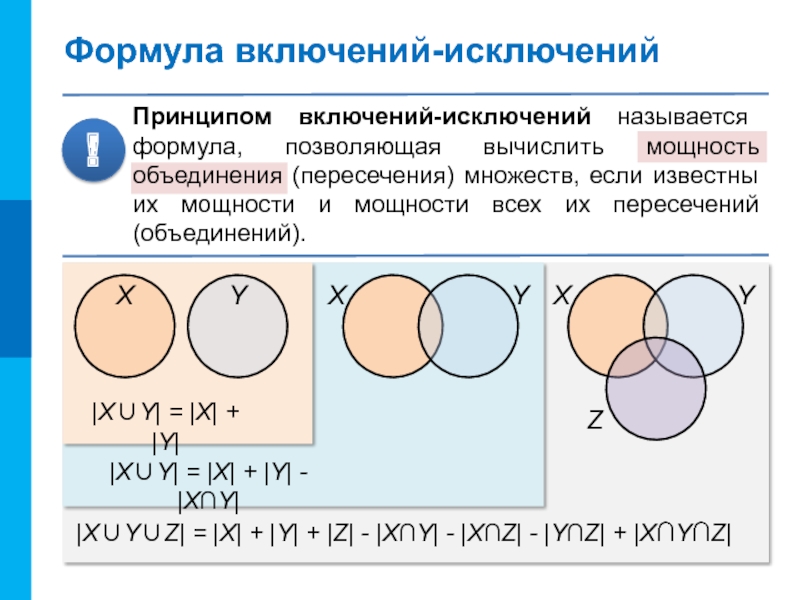
- 13. Формула включений-исключенийПринципом включений-исключений называется формула, позволяющая вычислить
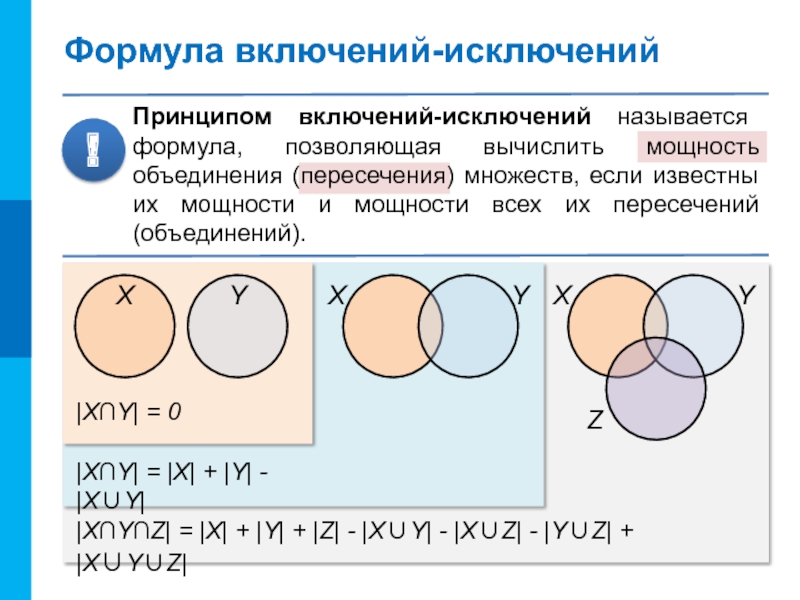
- 14. Формула включений-исключенийПринципом включений-исключений называется формула, позволяющая вычислить
- 15. - 10Вопросы и заданияВ зимний лагерь отправляется
- 16. Самое главноеМножество — это совокупность объектов произвольной
- 17. Вопросы и задания1. Сколько натуральных чисел от
- 18. 1) 1 ∪ 2 ∪ 3 ∪
- 19. Вопросы и задания3. Из 100 человек 85
- 20. Информационные источникиhttp://www.unikru.ru/userfiles/zoo-animal-friends-angela-waye.jpghttp://download.4-designer.com/files/20140221/Childlike-cartoon-alphabet-vector-material-62504.jpghttp://s4.pic4you.ru/y2014/07-04/12216/4477117.pnghttp://azbukadekor.ru/upload/iblock/475/475cddb0ce49566682e02adfdffd946e.jpghttp://st.gdefon.com/wallpapers_original/s/580857_babochki_raznotsvetnyie_radujnyie_5500x3765.jpghttps://pixabay.com/static/uploads/photo/2013/07/12/13/16/pencil-146715__180.png
- 21. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Ключевые слова
множество
пустое множество
пересечение двух множеств
объединение двух множеств
дополнение множества
мощность множества
Слайд 3Понятие множества
Множество — совокупность объектов произвольной природы, которая рассматривается как
единое целое.
!
Слайд 5Стандартные обозначения
Множества принято обозначать прописными буквами латинского алфавита (A, B,
C, …). Объекты, входящие в состав множества, называются его элементами
и обозначаются строчными латинскими буквами.Слайд 6Круги Эйлера
Для наглядного изображения множеств используются круги Эйлера.
Точки внутри
круга считаются элементами множества.
x ∈ M
x ∉ M
Слайд 7Подмножество
Если каждый элемент множества P принадлежит множест-
ву М, то говорят,
что P есть подмножество М, и записывают:
P ⊂ М
Само множество
М является своим подмножеством:
М ⊂ МПустое множество является подмножеством М:
∅ ⊂ М
Универсальное множество содержит все возможные подмножества одной приро-ды. Обозначается буквой U.
P ⊂ М
Слайд 8Множества M и X не имеют общих элементов: M ∩ X
= ∅
P подмножество множества М:
М ∩ P = P
Пересечение множеств
М и М:
М ∩ М = МX ∩ Y
Пересечение множеств
Пересечением двух множеств X и Y называется множество их общих элементов. Обозначается X ∩ Y.
!
X
Y
X ∩ Y
Слайд 9X ∪ Y
Объединение множеств
Объединением двух множеств X и Y называется
мно-жество, состоящее из всех элементов этих множеств и не содержащее
никаких других элементов (X ∪ Y).!
M ∪ ∅ = М
P подмножество множества М:
М ∪ P = М
Объединение множеств М и М:
М ∪ М = М
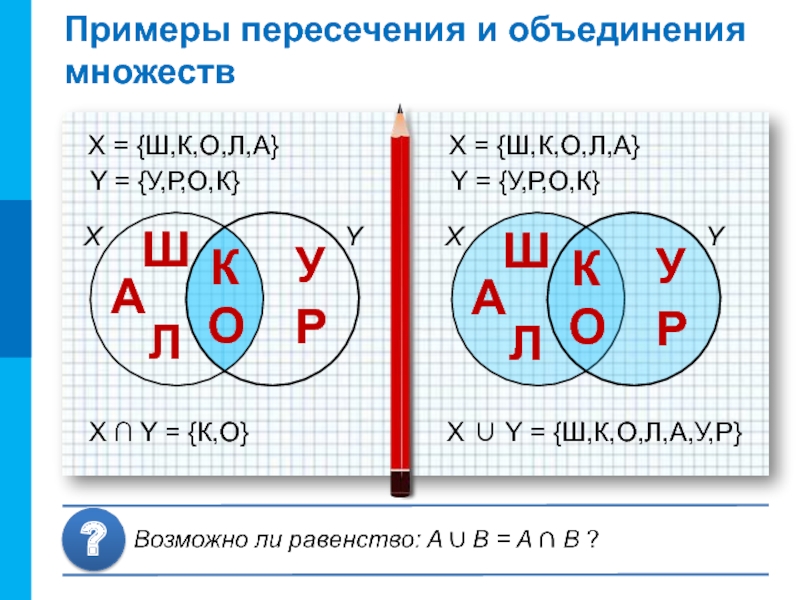
Слайд 10Примеры пересечения и объединения множеств
X
Y
X ∪ Y = {Ш,К,О,Л,А,У,Р}
X =
{Ш,К,О,Л,А}
Y = {У,Р,О,К}
X ∩ Y = {К,О}
X
Y
Ш
Л
А
К
О
У
Р
Ш
Л
А
К
О
У
Р
?
X = {Ш,К,О,Л,А}
Y =
{У,Р,О,К}Слайд 11Дополнение множества
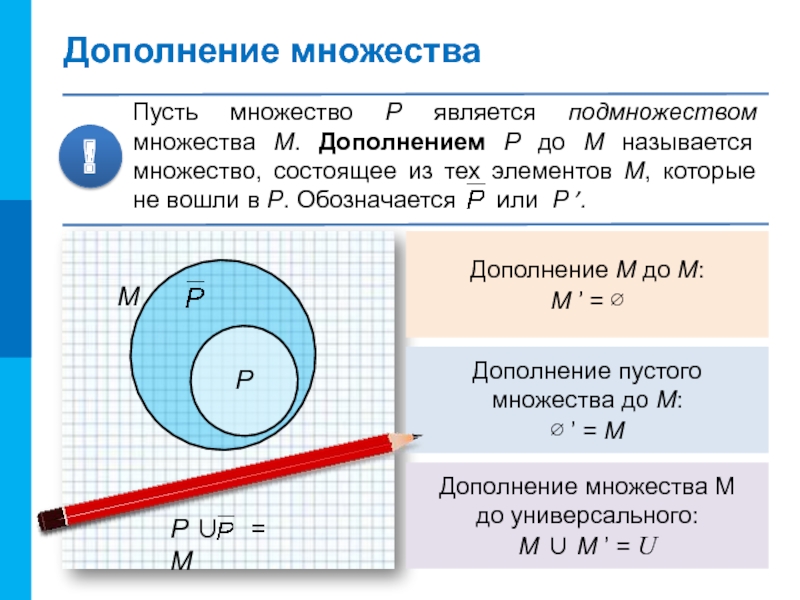
Пусть множество P является подмножеством множества М. Дополнением P
до М называется множество, состоящее из тех элементов М, которые
не вошли в P. Обозначается или P ’.!
Дополнение М до М:
М ’ = ∅
Дополнение пустого
множества до М:
∅ ’ = М
Дополнение множества М
до универсального:
M ∪ M ’ = U
P ∪ = M
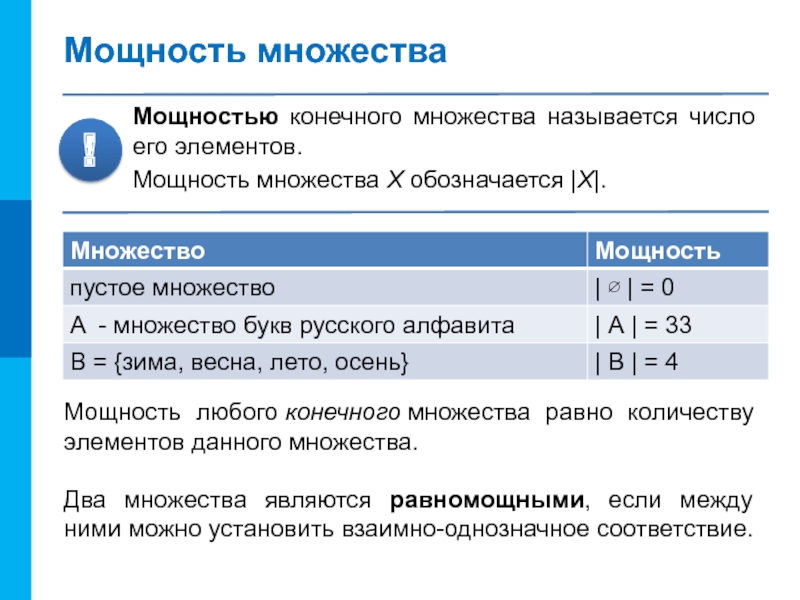
Слайд 12Мощность множества
Мощностью конечного множества называется число его элементов.
Мощность множества
X обозначается |X|.
!
Мощность любого конечного множества равно количеству элементов данного множества.
Два множества
являются равномощными, если между ними можно установить взаимно-однозначное соответствие.Слайд 13Формула включений-исключений
Принципом включений-исключений называется формула, позволяющая вычислить мощность объединения (пересечения)
множеств, если известны их мощности и мощности всех их пересечений
(объединений).!
Слайд 14Формула включений-исключений
Принципом включений-исключений называется формула, позволяющая вычислить мощность объединения (пересечения)
множеств, если известны их мощности и мощности всех их пересечений
(объединений).!
Слайд 15- 10
Вопросы и задания
В зимний лагерь отправляется 100 старшеклассников. Почти
все они увлекаются сноубордом, коньками или лыжами. При этом многие
из них занимаются несколькими видами спорта. Всего кататься на сноуборде умеют 30 ребят, на лыжах — 28, на коньках — 42. Умением кататься на лыжах и сноубор-де могут похвастаться 8 ребят, на лыжах и коньках — 10, на сноуборде и коньках — 5, но только трое из них владеют всеми тремя видами спорта. Сколько ребят не умеет кататься ни на сноуборде, ни на лыжах, ни на коньках?Решение:
|S∪L∪K| = |S| + |L| + |K| - |S∩L| - |S∩K| - |L∩K| + |S∩L∩K|=
= 30
Обозначим через S, L и K множество сноубордистов, лыж-ников и любителей коньков соответственно. Тогда:
Ответ: 20 старшеклассников
+ 28
+ 42
- 8
- 5
+ 3
=80
=> 100 - 80 = 20
Слайд 16Самое главное
Множество — это совокупность объектов произвольной природы, которая рассматривается
как единое целое.
Пересечением двух множеств X и Y называется множество
их общих элементов.Объединением двух множеств X и Y называется множество, состоящее из всех элементов этих множеств и не содержащее никаких других элементов.
Пусть множество P является подмножеством множест- ва М. Дополнением P до М называется множество, состоящее из тех элементов М, которые не вошли в P.
Мощностью конечного множества называется число его элементов.
Слайд 17Вопросы и задания
1. Сколько натуральных чисел от 1 до 1000
включительно делятся на 3 или на 5, или на 7?
[1000:3]
= 333 чисел делятся на 3[1000:5] = 200 чисел делятся на 5
[1000:7] = 142 числа делятся на 7
[1000:(3·5)] = 66 чисел делятся на 3 и 5
[1000:(3·7)] = 47 чисел делятся на 3 и 7
[1000:(5·7)] = 28 чисел делятся на 5 и 7
[1000:(3·5·7)] = 9 чисел делятся на 3, 5 и 7
По формуле включений-исключений |X∪Y∪Z| = |X| + |Y| + |Z| - |X∩Y| - |X∩Z| - |Y∩Z| + |X∩Y∩Z|
получаем: 333 + 200 +142 – 66 – 47 – 28 + 9 = 543
Ответ: 543 числа
Решение:
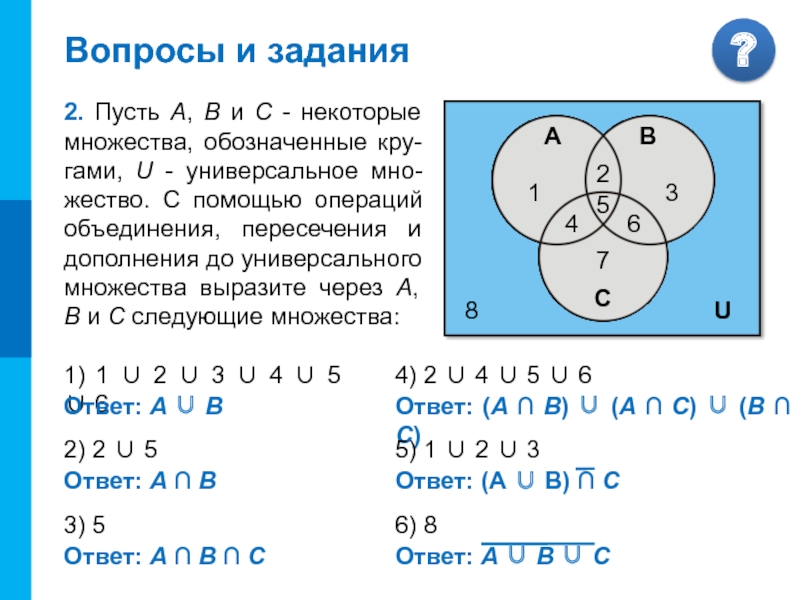
Слайд 181) 1 ∪ 2 ∪ 3 ∪ 4 ∪ 5
∪ 6
Ответ: А ∪ В
2) 2 ∪ 5
Ответ: А
∩ В 3) 5
Ответ: А ∩ В ∩ С
4) 2 ∪ 4 ∪ 5 ∪ 6
Ответ: (А ∩ В) ∪ (А ∩ С) ∪ (В ∩ С)
5) 1 ∪ 2 ∪ 3
6) 8
Вопросы и задания
2. Пусть A, B и C - некоторые множества, обозначенные кру-гами, U - универсальное мно-жество. С помощью операций объединения, пересечения и дополнения до универсального множества выразите через A, B и C следующие множества:
Слайд 19Вопросы и задания
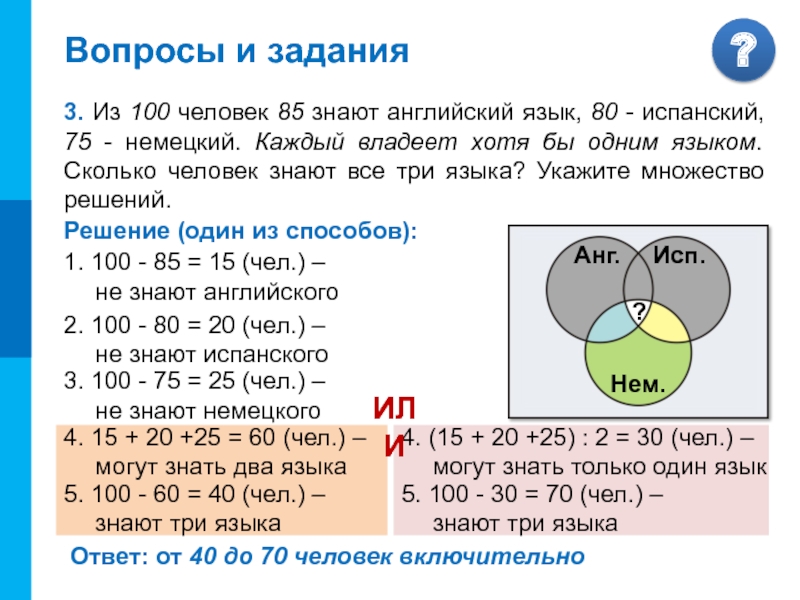
3. Из 100 человек 85 знают английский язык,
80 - испанский, 75 - немецкий. Каждый владеет хотя бы
одним языком. Сколько человек знают все три языка? Укажите множество решений.Решение (один из способов):
1. 100 - 85 = 15 (чел.) –
не знают английского
Ответ: от 40 до 70 человек включительно
2. 100 - 80 = 20 (чел.) –
не знают испанского
3. 100 - 75 = 25 (чел.) –
не знают немецкого
4. 15 + 20 +25 = 60 (чел.) –
могут знать два языка
5. 100 - 60 = 40 (чел.) –
знают три языка
4. (15 + 20 +25) : 2 = 30 (чел.) –
могут знать только один язык
5. 100 - 30 = 70 (чел.) –
знают три языка
ИЛИ