ошибкой r.
Средняя ошибка вычисляется по формуле
(15)При нормальном распределении средняя ошибка v связана со средней квадратичеcкой ошибкой m примерным соотношением
(16)










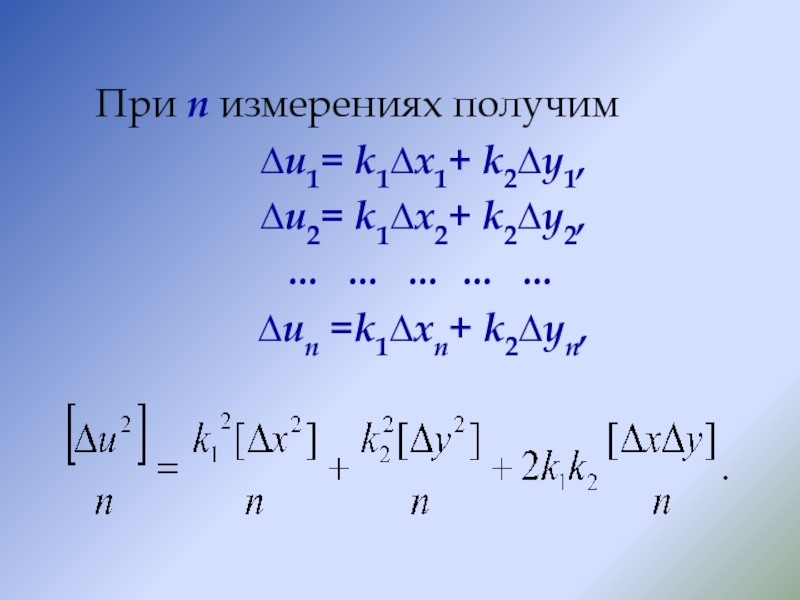

















![Нормальное распределение Указанные поправки обладают еще одним важным свойством [v2] Указанные поправки обладают еще одним важным свойством [v2] = min, (19) т.е.](/img/thumbs/81a7e4d2924d0c91cd08bded45d98bf2-800x.jpg)



![Нормальное распределение Отсюда nm2=m2 +[v2], m2(n–1)=[v2], Отсюда nm2=m2 +[v2], m2(n–1)=[v2],](/img/thumbs/d3b61e9fbcdf49354f03308dd8b83e40-800x.jpg)
![Нормальное распределение Вычисление величины [v2] контролируется по формулам [v2] = – Вычисление величины [v2] контролируется по формулам [v2] = – [v l ] ,](/img/thumbs/878c0b8dc21ce39616690224aaacfc73-800x.jpg)