Слайд 1Обработка экспериментальных данных
Слайд 2АППРОКСИМАЦИЯ ФУНКЦИЙ
На практике часто не известна аналитическая зависимость между x
и y, т.е. функцию нельзя записать в виде y=f(x). В
некоторых случаях эта зависимость известна, но вычисления значений функций громоздко. В этих случаях прибегают к табличному способу задания функций. Таблица представляет собой набор значений функций для последующих значений аргументов:
x x0 x1 … xn
y y0 y1 … yn
Эти значения либо вычислены, либо получены экспериментально.
Слайд 3Возникает задача о приближении (аппроксимации) функции: данную функцию y=f(x) требуется
приближенно заменить (аппроксимировать) некоторой функцией Y(x) так, чтобы отклонения (в
некотором смысле) Y(x) от f(x) в заданной области было наименьшим. Функция Y(x) называется аппроксимирующей.
Слайд 4Интерполяция
Пусть на отрезке [x0, xn] задана функция y=f(x) своими n+1
значениями:
y0=f(x0), y1=f(x1), …, yn=f(xn) в точках x0, x1, …, xn,
которые назовем узлами интерполяции. Предполагается, что при . Требуется найти аналитическое выражение Y(x) функции, заданной таблично, которая в узлах интерполяции совпадает со значениями заданной функции, т.е.
y0=Y(x0), y1=Y(x1), …, yn=Y(xn).
Процесс вычисления значений функции в точках x, отличных от узлов интерполяции, называют интерполированием функции f(x).
Слайд 5Если x находится за пределами отрезка [x0, xn], то задача
отыскания значения функции в точке x называется экстраполированием.
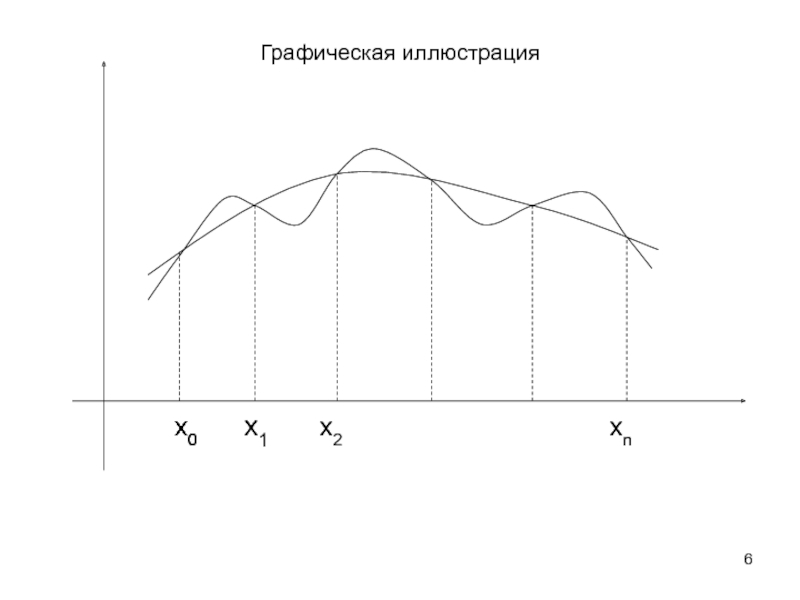
Геометрически задача
интерполирования для функции одной переменой y=f(x) означает построение кривой, проходящей через точки плоскости с координатами
(x0, y0), (x1, y1), …, (xn, yn)
Слайд 6Графическая иллюстрация
x0
x0
x0
x1
x2
xn
Слайд 7Линейная интерполяция
Отыскивается интервал [xi-1, xi], в который попадает значение
x, необходимо вычислить y=f(x).
На отрезке [xi-1, xi] заменим дугу кривой
y=f(x) стягивающей её хордой
x0
x0
xi
xn
xi-1
x
x
y
Y=f(x)
хорда
(Xi-1,yi-1)
(Xi,yi)
Слайд 9Интерполяционный многочлен Лагранжа
Пусть функция задана таблично
Построим многочлен Ln(x), такой, что
Ln(x0)=
y0, Ln(x1)= y1, …, Ln(xn)= yn.
Задача имеет решение, если
степень многочлена Ln(x) будет не выше n.
Слайд 10Метод наименьших квадратов
Иногда целесообразней строить функцию, график которой проходит
«близко» от заданных точек. Пусть функция задана таблицей:
Нужно найти эмпирическую
зависимость y=f(x), значение которых при x=xi мало отличались бы от опытных данных yi. График функции y=f(x), вообще говоря, не проходит через точки (xi, yi), как в случае интерполяции, что приводит к сглаживанию экспериментальных данных.
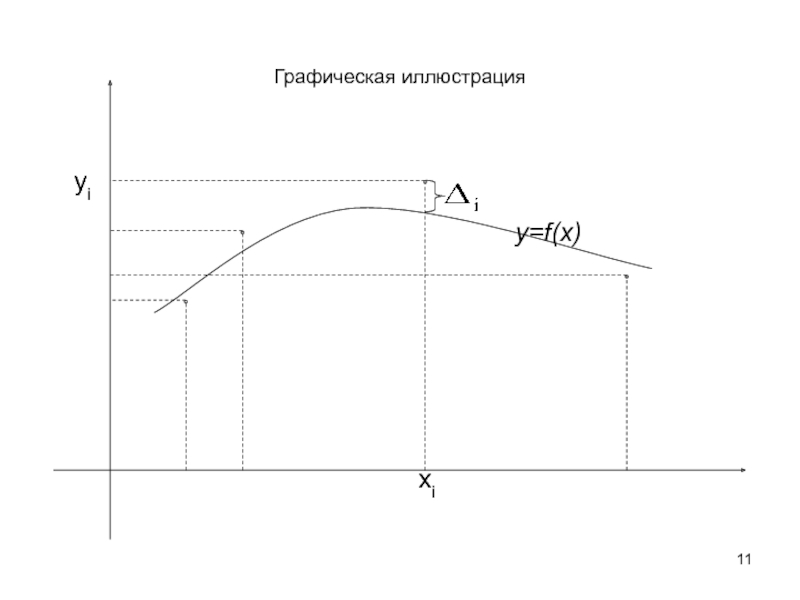
Слайд 11Графическая иллюстрация
xi
yi
y=f(x)
Слайд 12Построение эмпирической формулы состоит из двух этапов:
1) выбор общего вида
зависимости;
2) выбор наилучших значений параметров, входящих в формулу.
Пусть тип эмпирической
зависимости выбран, и ее можно записать в виде: , где f – известная функция; - неизвестные постоянные параметры, значения которых надо найти.
В каждой точке xi вычислим разность между табличным значением функции yi и вычисленным значением функции , значения
, назовем отклонениями
Слайд 13Сумма квадратов отклонений для всех точек:
является функцией от независимых переменных
,
то есть
Параметры будем находить из условия минимума функции S.
Минимум найдем, приравнивая к нулю частные производные по этим переменным
Из системы (*) найдем .
Слайд 14
Геометрически метод наименьших квадратов можно интерпретировать так: среди бесконечного множества
линий данного вида, проведенных относительно данных экспериментальных точек, выбрать одну,
для которой сумма квадратов отклонений будет наименьшей.
Слайд 15Нахождение параметров линейной функции
Возьмем приближающую функцию в виде y=ax+b.
Тогда
Условия минимума запишутся так:
или
Слайд 16Нахождение параметров квадратичной функции



![Обработка экспериментальных данных ИнтерполяцияПусть на отрезке [x0, xn] задана функция y=f(x) своими n+1 значениями:y0=f(x0), ИнтерполяцияПусть на отрезке [x0, xn] задана функция y=f(x) своими n+1 значениями:y0=f(x0), y1=f(x1), …, yn=f(xn) в точках x0,](/img/thumbs/394c9845770b2dcee89639089e750f49-800x.jpg)
![Обработка экспериментальных данных Если x находится за пределами отрезка [x0, xn], то задача отыскания Если x находится за пределами отрезка [x0, xn], то задача отыскания значения функции в точке x называется](/img/thumbs/f89fc5d3ca323a80f2de0b80c5f5a6e0-800x.jpg)
![Обработка экспериментальных данных Линейная интерполяция Отыскивается интервал [xi-1, xi], в который попадает значение x, Линейная интерполяция Отыскивается интервал [xi-1, xi], в который попадает значение x, необходимо вычислить y=f(x).На отрезке [xi-1, xi]](/img/thumbs/79cd395ad3e852b370d1f3637935099a-800x.jpg)