называется такой угол x, для которого sinx=m, -π/2≤X≤π/2,|m|≤1
Функция y =
sinx непрерывна и ограничена на всей своей числовой прямой. Функция y = arcsinx является строго возрастающей.График обратной функции симметричен с графиком основной функции относительно биссектрисы I - III координатных углов.



![Обратные тригонометрические функции Свойства функции y = arcsin x 1)Область определения: отрезок [-1; 1]; Свойства функции y = arcsin x 1)Область определения: отрезок [-1; 1]; 2)Область изменения: отрезок](/img/thumbs/f9a4e3e14d4f4814c14e568f1a528437-800x.jpg)

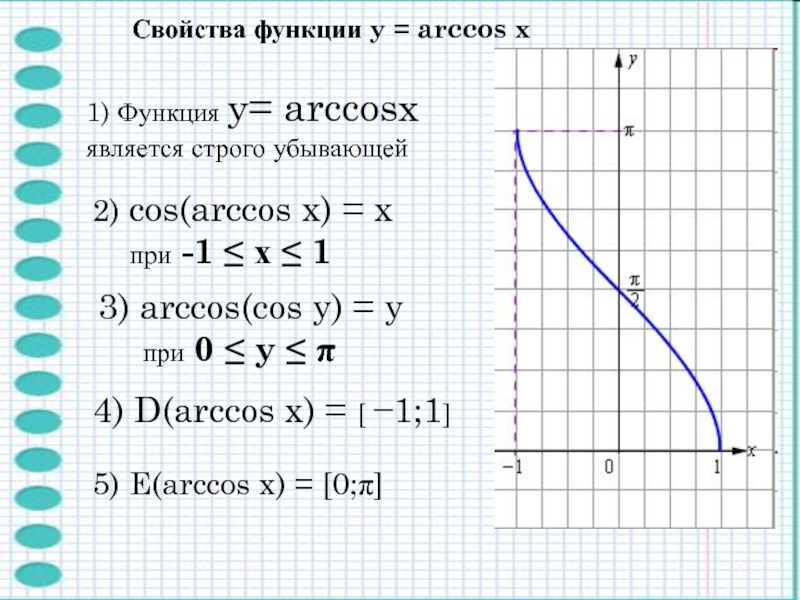

![Обратные тригонометрические функции y=arctgх1) Область определения: х є R 2) Область y=arctgх1) Область определения: х є R 2) Область значения: отрезок [-π/2,π/2];3)](/img/thumbs/d607c6f01359fd76e7b8f0e9cbb81680-800x.jpg)