Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Описанная и вписанная окружности треугольника
Содержание
- 1. Описанная и вписанная окружности треугольника
- 2. Готовимся к изучению новой темыПовторите теоремы параграфа
- 3. Окружность называют описанной около треугольника, если она
- 4. Около любого треугольника можно описать окружность
- 5. СледствияТри серединных перпендикуляра сторон треугольника пересекаются в
- 6. Следствие из второго следствия: как построить окружность,
- 7. Пример построения окружности, описанной около прямоугольного треугольника.1)
- 8. Окружность называют вписанной в треугольник, если она
- 9. В любой треугольник можно вписать окружностьО лежит
- 10. СледствияБиссектрисы углов треугольника пересекаются в одной точке.Центр окружности вписанной в треугольник, - это точка пересечения биссектрис.
- 11. Следствие из следствия. Чтобы построить окружность, вписанную
- 12. Пример построения окружности, вписанной в прямоугольный треугольникПользуясь
- 13. Задания для самостоятельной работыПостроить окружность, описанную около
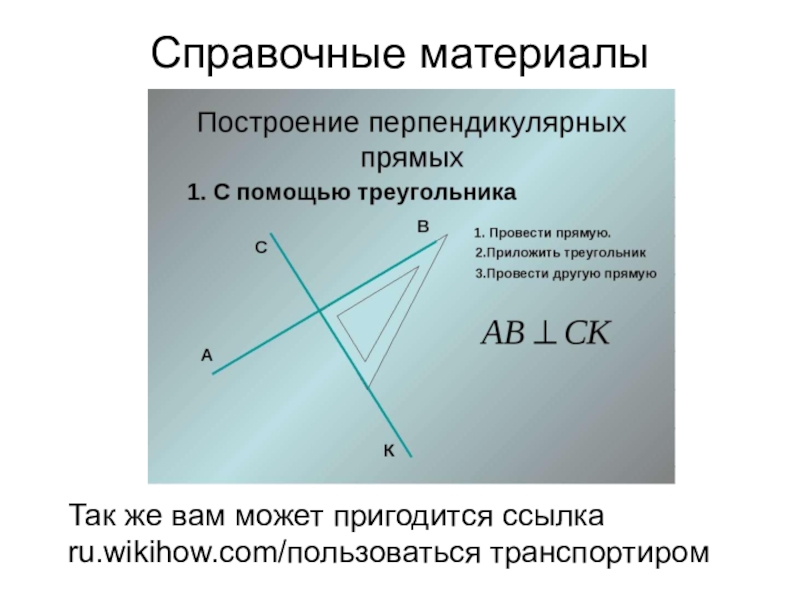
- 14. Справочные материалыТак же вам может пригодится ссылкаru.wikihow.com/пользоваться транспортиром
- 15. Скачать презентанцию
Готовимся к изучению новой темыПовторите теоремы параграфа 19. Ответьте на вопросыЧто такое геометрическое место точек?Что является геометрическим местом точек, равноудаленных от концов отрезка?Что является геометрическим местом точек, равноудаленных от сторон угла?
Слайды и текст этой презентации
Слайд 1Описанная и вписанная окружности треугольника
Учимся строить окружность описанную около треугольника
и вписанную в треугольник
Слайд 2Готовимся к изучению новой темы
Повторите теоремы параграфа 19. Ответьте на
вопросы
Что такое геометрическое место точек?
Что является геометрическим местом точек, равноудаленных
от концов отрезка?Что является геометрическим местом точек, равноудаленных от сторон угла?
Слайд 3Окружность называют описанной около треугольника, если она проходит через все
вершины треугольника
На приведенных ниже рисунках найдите тот, на котором изображена
окружность, описанная около треугольника.а
б
в
г
Слайд 4Около любого треугольника можно описать окружность
Точка О должна находится на равном расстоянии
от точек А и В.Дано: ∆АВС
Док-ть что существует точка О, такая, что ОА = ОВ = ОС
Док-во:
А
О
В
С
Значит О принадлежит срединному перпендикуляру,
проведенному к стороне АВ. Также О должна
находится на равном расстоянии от точек В и С. Значит О принадлежит срединному перпендикуляру,
проведенному к стороне ВС. Тогда О – точка пересечения этих серединных перпендикуляров.
Слайд 5Следствия
Три серединных перпендикуляра сторон треугольника пересекаются в одной точке.
Центр
окружности описанной около треугольника, - это точка пересечения серединных перпендикуляров
его сторон.
Слайд 6Следствие из второго следствия: как построить окружность, описанную около треугольника.
С
помощью линейки отметить середины двух любых сторон;
Через отмеченные точки с
помощью линейки и угольника провести перпендикуляры к сторонам;Отметить точку пересечения перпендикуляров – это центр описанной окружности;
Поставьте иглу циркуля в центр окружности, а ножку в одну из вершин, проведите окружность.
Слайд 7Пример построения окружности, описанной около прямоугольного треугольника.
1) С помощью линейки
отмечаем середины сторон АС и ВС, обозначим их М и
К;С
А
В
М
К
2) Через точки М и К с помощью
линейки и угольника провести
перпендикуляры к сторонам АС
и АВ;
3) Отметим точку пересечения
перпендикуляров – это центр
описанной окружности;
О
4) Проведем циркулем окружность радиусом ОА
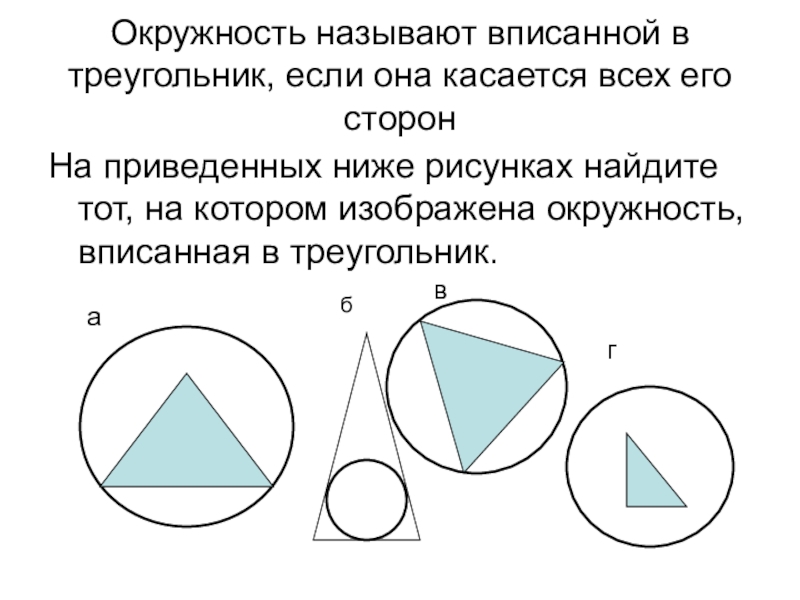
Слайд 8Окружность называют вписанной в треугольник, если она касается всех его
сторон
На приведенных ниже рисунках найдите тот, на котором изображена окружность,
вписанная в треугольник.а
б
в
г
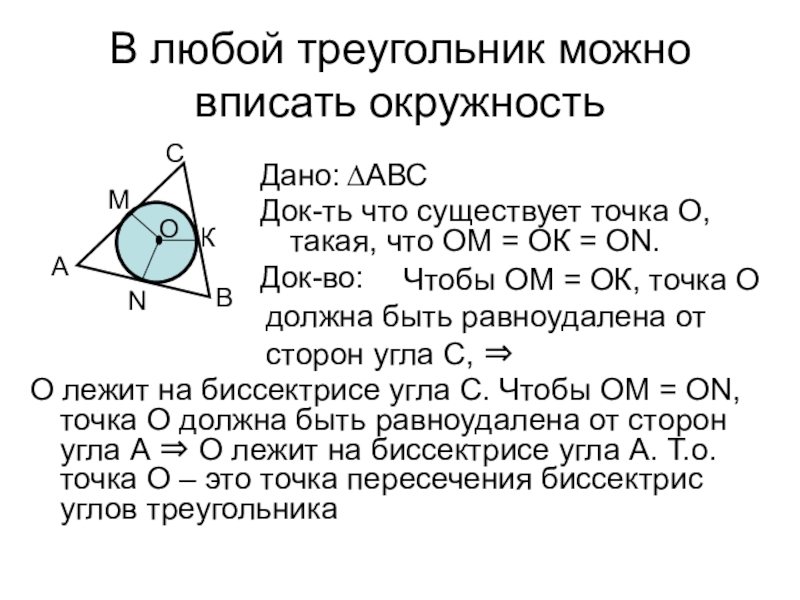
Слайд 9В любой треугольник можно вписать окружность
О лежит на биссектрисе угла
С. Чтобы ОМ = ОN, точка О должна быть равноудалена
от сторон угла А О лежит на биссектрисе угла А. Т.о. точка О – это точка пересечения биссектрис углов треугольникаДано: ∆АВС
Док-ть что существует точка О, такая, что ОМ = ОК = ОN.
Док-во:
А
О
С
В
М
К
N
Чтобы ОМ = ОК, точка О должна быть равноудалена от сторон угла С,
Слайд 10Следствия
Биссектрисы углов треугольника пересекаются в одной точке.
Центр окружности вписанной в
треугольник, - это точка пересечения биссектрис.
Слайд 11Следствие из следствия. Чтобы построить окружность, вписанную в треугольник, надо:
Пользуясь
транспортиром, провести биссектрисы двух любых углов треугольника;
Отметить точку их пересечения
– это центр вписанной окружности;Из этой точки опустить перпендикуляр на сторону;
Поставить иглу циркуля в центр окружности, а ножку в основание перпендикуляра и провести окружность.
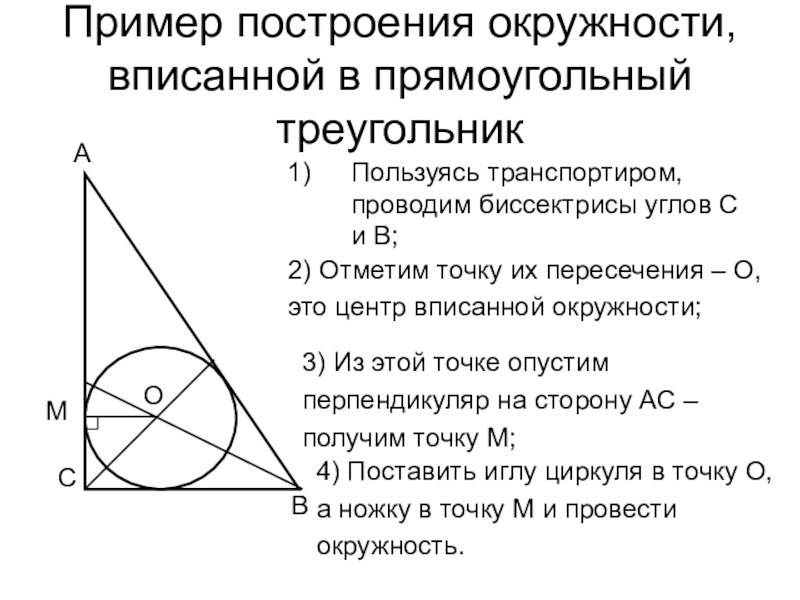
Слайд 12Пример построения окружности, вписанной в прямоугольный треугольник
Пользуясь транспортиром, проводим биссектрисы
углов С и В;
С
В
А
2) Отметим точку их пересечения – О,
это
центр вписанной окружности;О
3) Из этой точке опустим
перпендикуляр на сторону АС –
получим точку М;
М
4) Поставить иглу циркуля в точку О,
а ножку в точку М и провести
окружность.
Слайд 13Задания для самостоятельной работы
Построить окружность, описанную около тупоугольного треугольника.
Построить окружность,
вписанную в равнобедренный треугольник.
Каждый шаг подробно пояснять.
Форма оценивания: зачет/ незачет.
Слайд 14Справочные материалы
Так же вам может пригодится ссылка
ru.wikihow.com/пользоваться транспортиром
