Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определение вектора. Векторы на плоскости и в пространстве. Линейные операции
Содержание
- 1. Определение вектора. Векторы на плоскости и в пространстве. Линейные операции
- 2. Определение 1. Вектор – отрезок прямой, характеризующийся численным
- 3. Даны четыре точки А(1; 2; 3), С(7;
- 4. Определение 2.Нулевой вектор – любая точка плоскости, обозначается
- 5. Определение 6. Суммой векторов а (а1;
- 6. Даны точки А(2;7;-3), В(1;0;3)С(-3;-4;5), Д(-2;3;1),К(1;3;5),М(6;8;-3)Найдите :Решить задачу
- 7. Геометрически сложение векторов выглядит так:- для неколлинеарных векторов:
- 8. Исходные данные: векторы a и b . Для выполнения
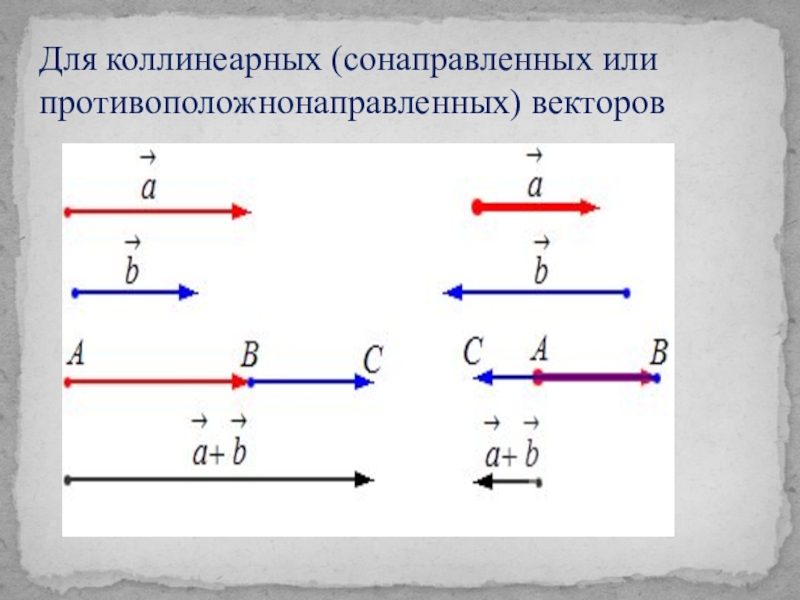
- 9. Для коллинеарных (сонаправленных или противоположнонаправленных) векторов
- 10. Сложение нескольких векторов
- 11. Отдельной схемы действия по вычитанию векторов нет, т.к. по
- 12. Произведением вектора (а1; а2) на
- 13. Исходные данные: 1) вектор a и число k=2;
- 14. Найдите произведение векторов АВ и СД на
- 15. Скачать презентанцию
Определение 1. Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху . При наличии конкретных точек границ обозначение вектора выглядит как две
Слайды и текст этой презентации
Слайд 2Определение 1. Вектор – отрезок прямой, характеризующийся численным значением и направлением.
Вектор обозначается строчной латинской буквой со стрелкой сверху
. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы(маркирующие границы вектора) также со стрелкой сверху.
Координатами вектора с началом в точке А1 (х1; у1; z1) и концом в точке А2 (х2; у2; z2 ) называются числа
х2 - х1, у2 - у1, z2 - z1
Слайд 3Даны четыре точки
А(1; 2; 3), С(7; 5; 4),
В(4; 5;
6), Д(-8; 10; 9)
Найти координаты векторов:
Решить задачу
Слайд 4Определение 2.Нулевой вектор – любая точка плоскости, обозначается как нуль со
стрелкой сверху
Определение 3.Длина вектора – величина, равная или большая нуля, определяющая
длину отрезка, составляющего вектор. Длина вектора обозначается Определение 4.Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными
Определение 5.Равными называются векторы, имеющие одинаковые длины (равные координаты) и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости
Слайд 5Определение 6. Суммой векторов
а (а1; а2; а3) и
в(в1; в2; в3) называется вектор
с(а1 + в1 ;
а2 + в2; а3 + в3) Слайд 8Исходные данные: векторы a и b . Для выполнения над ними операции
сложения необходимо из произвольной точки отложить вектор AB равный вектору а из
полученной точки– вектор −ВС равный вектору b. Соединив точки и Аи C, получаем отрезок (вектор) −АС, который и будет являться суммой исходных данных. Иначе описанную схему сложения векторов называют правилом треугольникаСлайд 11Отдельной схемы действия по вычитанию векторов нет, т.к. по сути разность векторов
есть сумма векторов
Определение 7. Вычитание векторов
Слайд 12Произведением вектора (а1; а2) на число к называется
вектор
= (ка1; ка2; )
Если к >0, то вектор к а совпадает с направлением вектора а Если к <0, то противоположно направлен
Определение 8. Умножение вектора на число