Определенный интеграл. Понятие. Геометрический смысл. Свойства

Содержание

1. Определенный интеграл. Понятие. Геометрический смысл. Свойства
2. Задача, приводящая к понятию определенного интеграла2. Определение определенного интеграла. Теорема существования 3. Свойства определенного интеграла Вопросы
3. Слайд 3
4. Задача, приводящая к понятию определенного
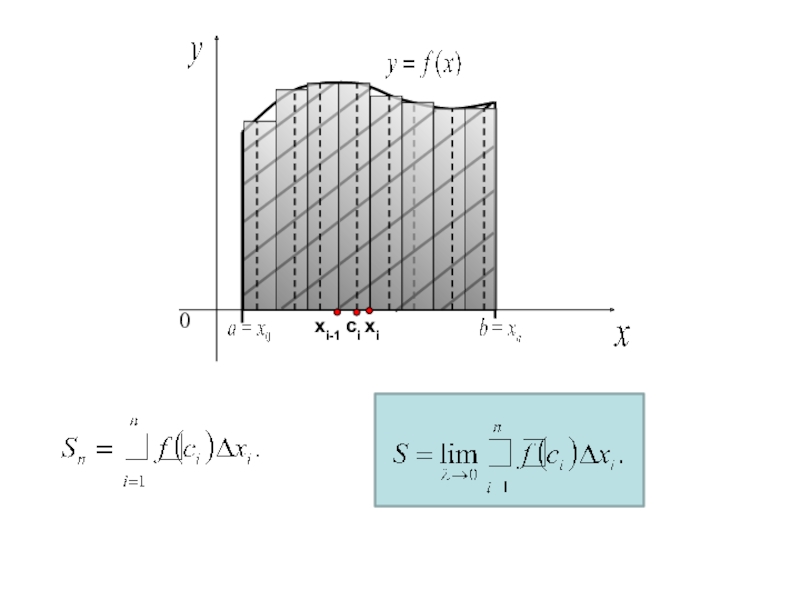
5. 0xixi-1ci
6. 2. Определение определенного интеграла. Теорема существованияПусть
7. Опр. Если существует и конечен предел интегральной
8. Геометрический смысл определенного интегралаЕсли
9. Теорема . (существования определенного интеграла) Если функция
10. 3. Свойства определенного интеграла1. Определенный интеграл зависит
11. 4. 5. 6. 7. Если функция f(x)
12. 8.
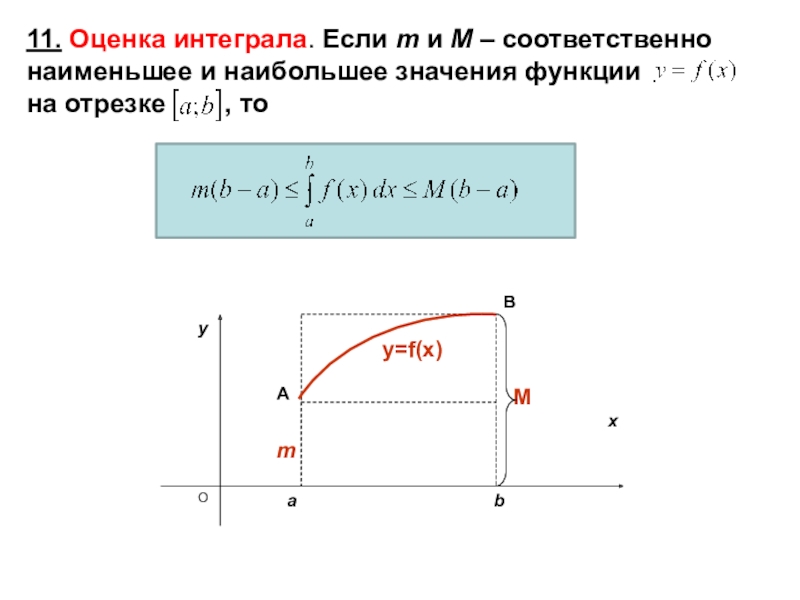
13. хy=f(x)11. Оценка интеграла. Если т и М
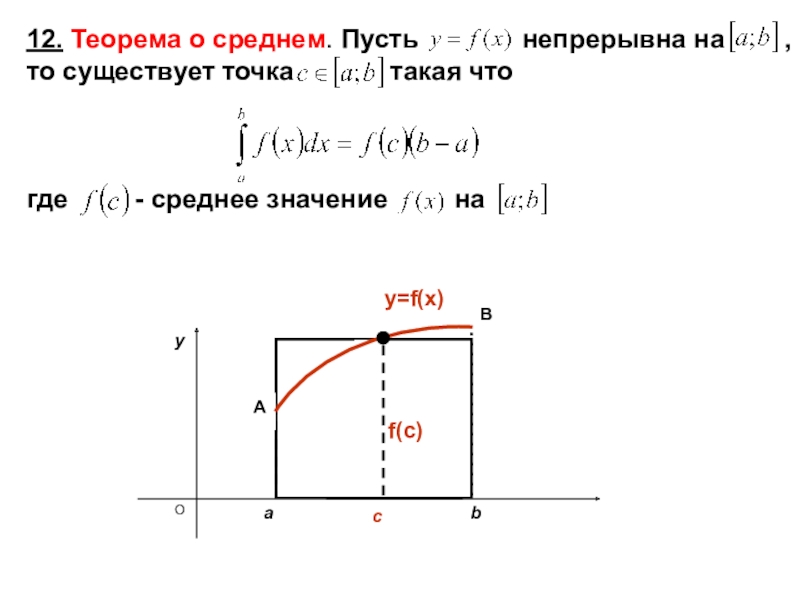
14. 12. Теорема о среднем. Пусть
15. Скачать презентанцию

Задача, приводящая к понятию определенного интеграла2. Определение определенного интеграла. Теорема существования 3. Свойства определенного интеграла Вопросы

Главная
Разное
Определенный интеграл. Понятие. Геометрический смысл. Свойства

Слайды и текст этой презентации

Слайд 1Определенный интеграл.
Понятие.
Геометрический смысл.
Свойства.

Слайд 2Задача, приводящая к понятию определенного интеграла

2. Определение определенного интеграла. Теорема

существования

3. Свойства определенного интеграла
Вопросы

Задача, приводящая к понятию определенного интеграла2. Определение определенного интеграла. Теорема существования 3. Свойства определенного интеграла Вопросы

Слайд 3

Слайд 4 Задача, приводящая к понятию
определенного интеграла
Задача: о

вычислении площади криволинейной трапеции
Опр. Криволинейной трапецией называется плоская фигура, ограниченная

сверху кривой , с боков двумя вертикальными линиями х=а и х=b и снизу осью ох.

Задача, приводящая к понятию определенного интеграла Задача: о вычислении площади криволинейной трапецииОпр. Криволинейной трапецией называется

Слайд 50
xi
xi-1
ci

Слайд 62. Определение определенного интеграла.
Теорема существования
Пусть

непрерывна на
(1) – интегральная сумма

2. Определение определенного интеграла. Теорема существованияПусть непрерывна на (1)

Слайд 7Опр. Если существует и конечен предел интегральной суммы (1) при

, не зависящий ни от

способа разбиения, ни от выбора промежуточных точек, то его называют определенным интегралом от функции на и обозначают

(2)

- нижний предел интегрирования
- верхний предел
- подынтегральное выражение
- подынтегральная функция
- переменная интегрирования

Опр. Если существует и конечен предел интегральной суммы (1) при , не

Слайд 8Геометрический смысл определенного интеграла
Если определена

и непрерывна на ,

на , то определенный интеграл от этой функции на численно равен площади соответствующей криволинейной трапеции

Слайд 9Теорема . (существования определенного интеграла) Если функция

непрерывна на , то

определенный интеграл от функции существует.

Опр. Функция называется интегрируемой на , если определенный интеграл для нее на этом отрезке существует.

Теорема . (существования определенного интеграла) Если функция непрерывна на

Слайд 103. Свойства определенного интеграла
1. Определенный интеграл зависит от пределов интегрирования

функции f(x) и не зависит от обозначения переменной интегрирования:
2.

3. Свойства определенного интеграла1. Определенный интеграл зависит от пределов интегрирования функции f(x) и не зависит от обозначения

Слайд 114.
5.
6.
7. Если функция f(x) сохраняет знак на

отрезке , где

, то интеграл имеет тот же знак, что и функция.
Если на отрезке , то

Слайд 128.

на ,

, то

9. Модуль интеграла не превосходит интеграла от модуля подынтегральной функции:

10. Если функция f(x) интегрируема на , то при любом расположении точек a, b, c (считая, что функция f(x) интегрируема на большем из получившихся отрезков) имеет место формула