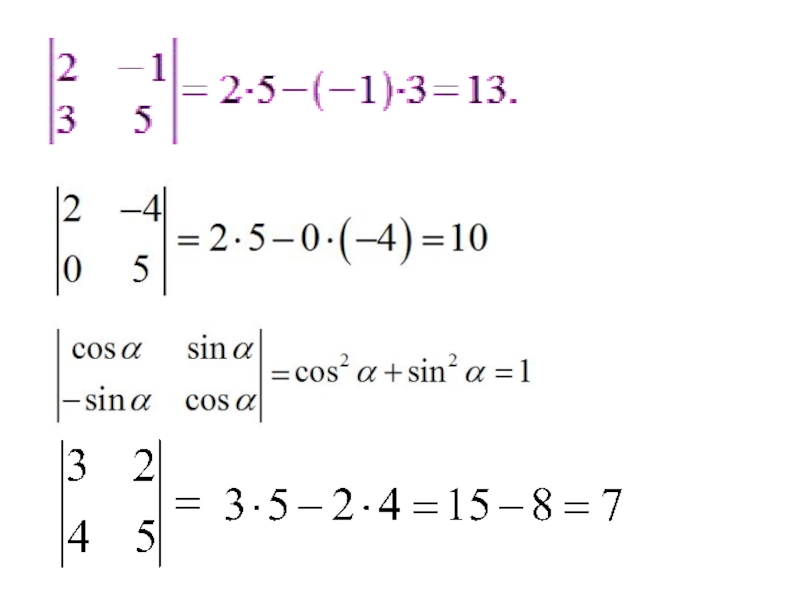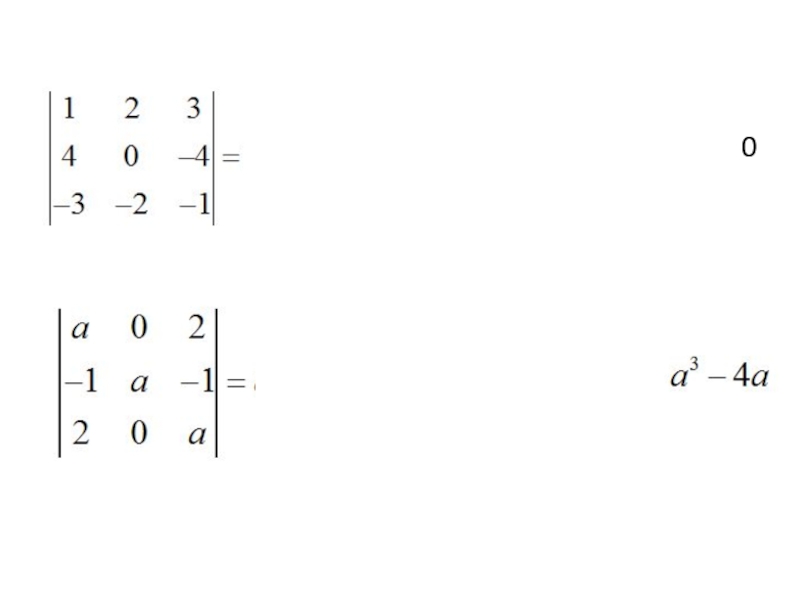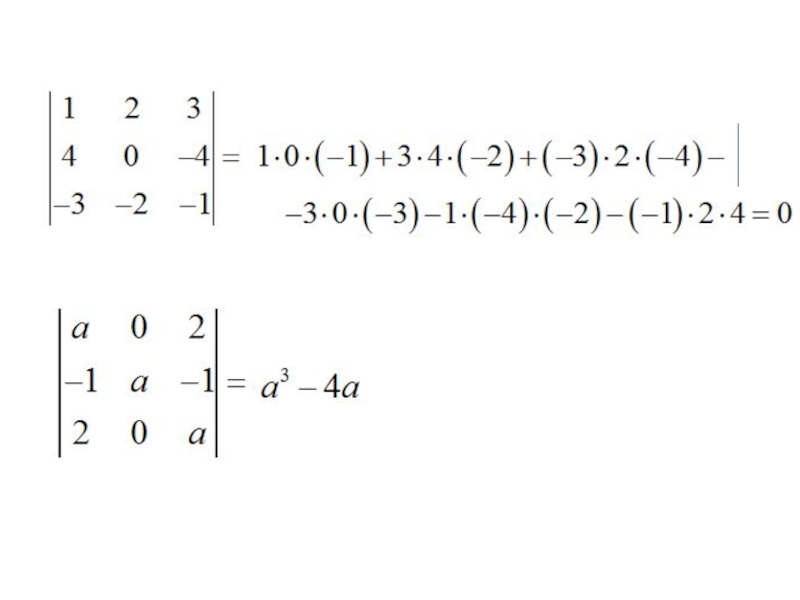матрицы по определенному правилу, которое будет сформулировано после введения понятий
миноров и алгебраических дополнений элементов определителя.ОБОЗНАЧЕНИЯ
Определителем (детерминатором) II порядка, который соответствует квадратной матрице II порядка, именуется число, обозначаемое символом