Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Ориентирование
Содержание
- 1. Ориентирование
- 2. ТЕМА: ОРИЕНТИРОВАНИЕ ЛИНИЙ НА МЕСТНОСТИ. ПРЯМАЯ И
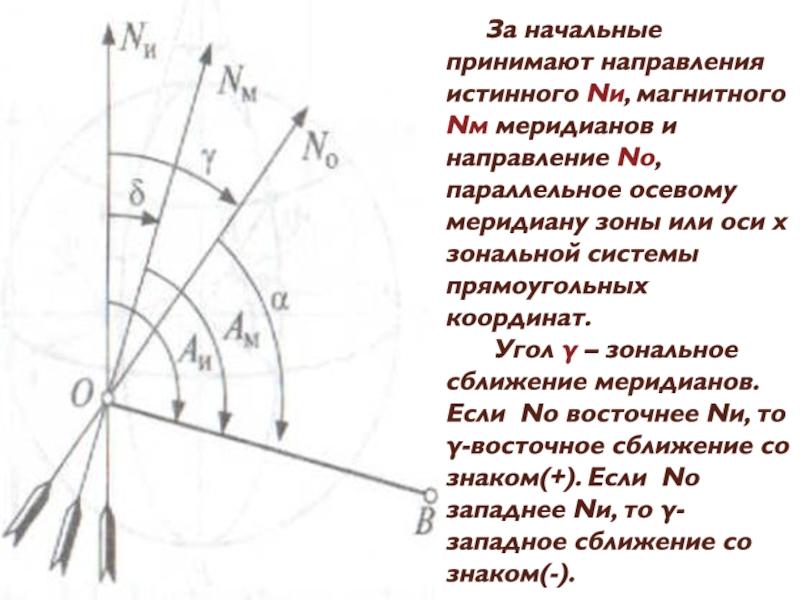
- 3. За начальные принимают направления истинного Nи, магнитного
- 4. Угол δ называется склонением магнитной стрелки. Если
- 5. Дирекционным углом α называется горизонтальный угол, отсчитываемый
- 6. Сближение меридиановПусть l- расстояние между точками А
- 7. При небольшом значении угла γ расстояние l
- 8. Зависимости между дирекционным углом, истинным и магнитным
- 9. Зависимость между истинным азимутом Аи линии ОВ
- 10. Для получения зависимости между дирекционным углом и магнитным азимутом приравняем правые части равенства:α+γ=Ам+δилиα=Ам+δ- γ
- 11. Прямые и обратные дирекционные углы и азимуты.Зависимость
- 12. Зависимости между истинными азимутами линий АВ и
- 13. Зависимость между дирекционными углами сторон ходаДирекционный угол
- 14. РумбыРумбом (r) называется горизонтальный угол (острый), отсчитываемый
- 15. Зависимость между дирекционными углами и румбами показана на рисунке, а формулы для перехода приведены в таблице.
- 16. Прямая и обратная геодезические задачи на плоскостиПрямая
- 17. Разности Δх и Δу координат точек последующей
- 18. С помощью румбов Δх и Δу можно
- 19. Обратная задача. По данным координатам точек А
- 20. Скачать презентанцию
ТЕМА: ОРИЕНТИРОВАНИЕ ЛИНИЙ НА МЕСТНОСТИ. ПРЯМАЯ И ОБРАТНАЯ ГЕОДЕЗИЧЕСКИЕ ЗАДАЧИ. Ориентированием линии называется определение ее направления на местности относительно некоторого направления, принятого за начальное.
Слайды и текст этой презентации
Слайд 2ТЕМА: ОРИЕНТИРОВАНИЕ ЛИНИЙ НА МЕСТНОСТИ. ПРЯМАЯ
И ОБРАТНАЯ ГЕОДЕЗИЧЕСКИЕ ЗАДАЧИ.
Ориентированием линии
Слайд 3 За начальные принимают направления истинного Nи, магнитного Nм меридианов и
направление No, параллельное осевому меридиану зоны или оси х зональной
системы прямоугольных координат. Угол γ – зональное сближение меридианов. Если Nо восточнее Nи, то γ-восточное сближение со знаком(+). Если Nо западнее Nи, то γ-западное сближение со знаком(-).
Слайд 4 Угол δ называется склонением магнитной стрелки. Если склонение восточное, то
знак(+), если склонение западное, то знак(-). Азимутом линии называется угол, отсчитываемый
от северного направления меридиана по ходу часовой стрелки до ориентируе мой линии. Азимуты могут иметь значения от О° до 360°. Азимут называют истинным Аи, если его измеряют от истинного меридиана Nи, и магнитным Aм, если его отсчитывают от магнитного мерндиана Nм.
Слайд 5
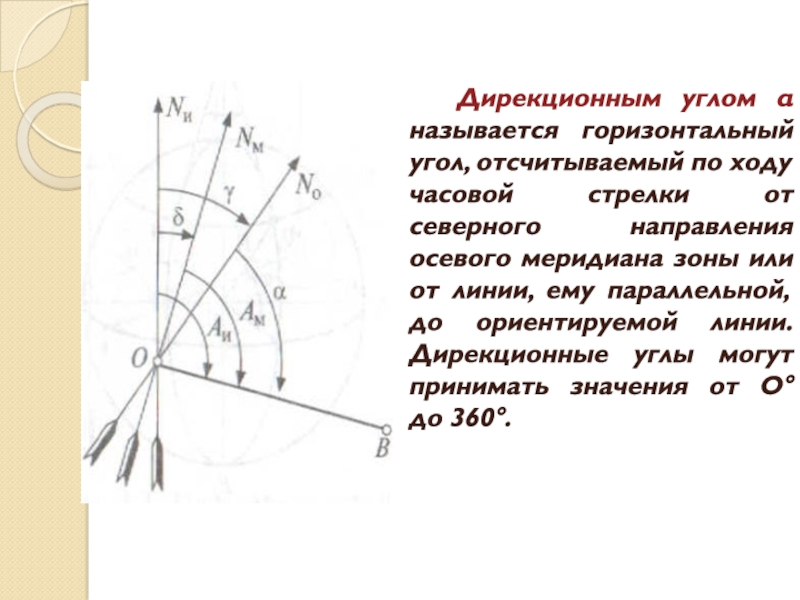
Дирекционным углом α называется горизонтальный угол, отсчитываемый по ходу часовой
стрелки от северного направления осевого меридиана зоны или от линии,
ему параллельной, до ориентируемой линии. Дирекционные углы могут принимать значения от О° до 360°.
Слайд 6Сближение меридианов
Пусть l- расстояние между точками А и В, расположенными
на параллели с широтой φ. Проведя в точках А и
В касательные к меридианам, проходящим через эти точки, в пересечении получим точку Т. Линии АТ и ВТ называются полуденными, а угол γ между ними – углом сближения меридианов, или сближением меридианов, в точках А и В.
Слайд 7 При небольшом значении угла γ расстояние l можно принять за
дугу радиуса ТА. Рассматривая спектр АТВ и треугольник ОАТ, можно
записатьγ = l /АТ,
АТ = Rtg(90° - φ°) = R/tgφ.
Следовательно
γ =( l /R)tgφ.
Выражая γ в минутах, получим
γ ´ =( l /R)tgφ*3438 ´.
При R=6371 км и l=1 км имеем
γ ´≈0,54tgφ.
Если известны долготы меридианов, проходящих через точки А и В, то сближение определяем по формуле
γ ≈Δλsinφ,
где Δλ-разность долгот меридианов, проходящих через точки А и В.
Слайд 8Зависимости между дирекционным углом, истинным и магнитным азимутами линии.
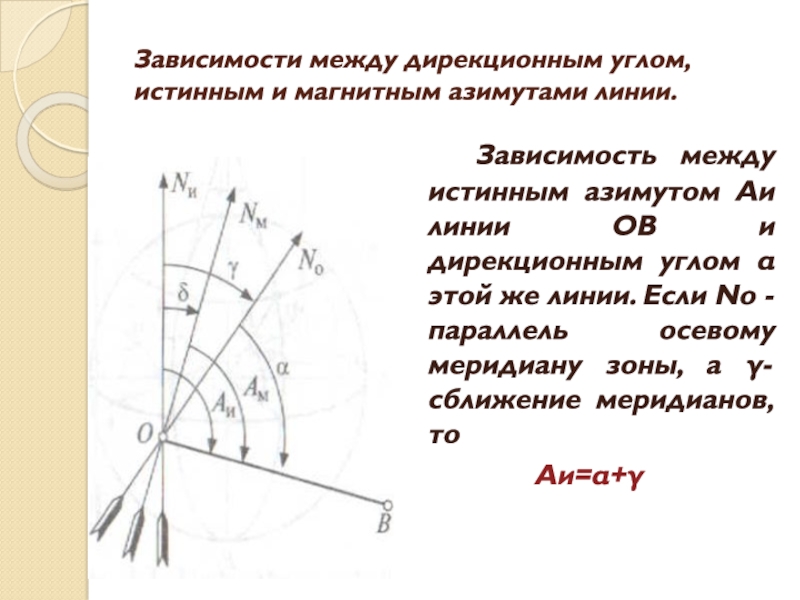
Зависимость между
истинным азимутом Аи линии ОВ и дирекционным углом α этой
же линии. Если No - параллель осевому меридиану зоны, а γ-сближение меридианов, тоАи=α+γ
Слайд 9 Зависимость между истинным азимутом Аи линии ОВ и магнитным азимутом
Ам этой же линии. δ – склонение магнитной стрелки. Тогда
Аи=Ам+δ.
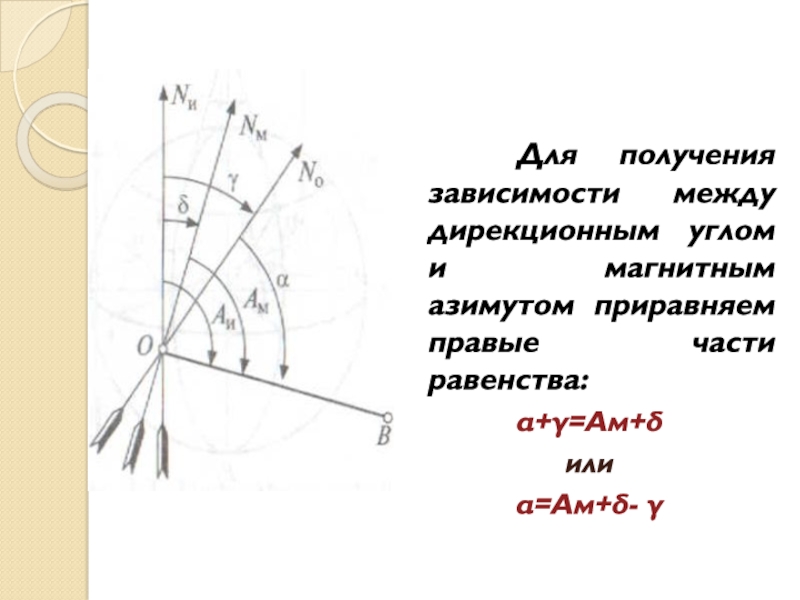
Слайд 10 Для получения зависимости между дирекционным углом и магнитным азимутом
приравняем правые части равенства:
α+γ=Ам+δ
или
α=Ам+δ- γ
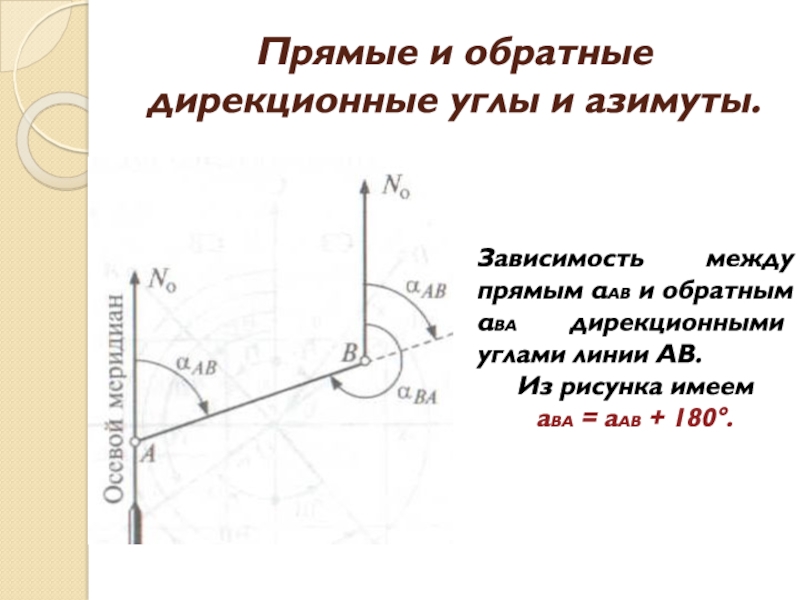
Слайд 11Прямые и обратные дирекционные углы и азимуты.
Зависимость между прямым αАВ
и обратным αВА дирекционными углами линии АВ.
Из рисунка имеем
аВА
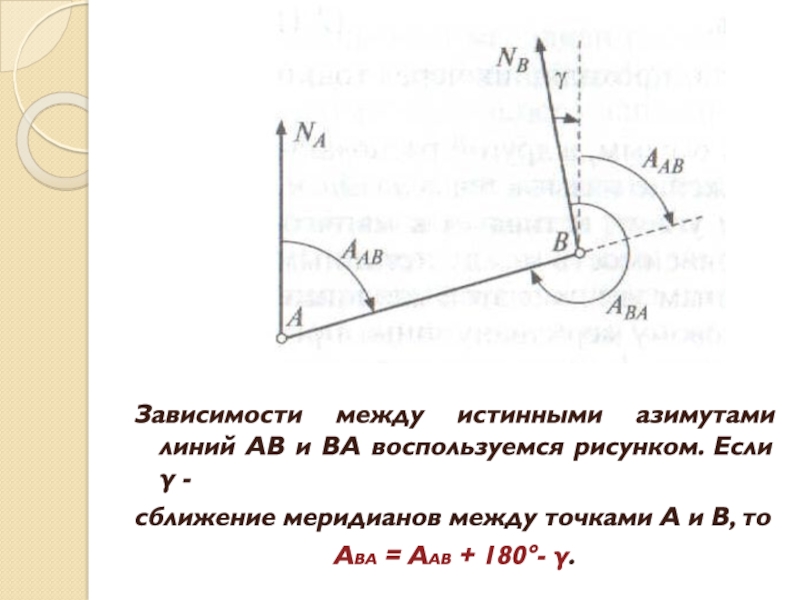
= аАВ + 180°.
Слайд 12Зависимости между истинными азимутами линий АВ и ВА воспользуемся рисунком.
Если γ -
сближение меридианов между точками А и В, то
АВА
= ААВ + 180°- γ.
Слайд 13Зависимость между дирекционными углами сторон хода
Дирекционный угол αАВ стороны АВ
будем считать известным. Если правый по ходу угол обозначить через
βп, тоαВС = αВА – βп.
Подставляя значение αВА из формулы , получим
αВС = αАВ + 180° – βп.
Если бы мы имели при точке В не правый, а левый угол βл , то получили бы формулу
αВС = αАВ + 180° – βл.
Слайд 14Румбы
Румбом (r) называется горизонтальный угол (острый), отсчитываемый от ближайшего (северного
или южного) направления меридиана до ориентируемой линии. Следовательно, румбы могут
принимать значения· только от О° до 90°.
Слайд 15 Зависимость между дирекционными углами и румбами показана на рисунке, а
формулы для перехода приведены в таблице.
Слайд 16Прямая и обратная геодезические задачи на плоскости
Прямая задача. Пусть АВ
- линия на местности, для которой известны ее горизонтальное проложение
(проекция линии на горизонтальную плоскость) d, дирекционный угол а и координаты начальной точки А (х1,у1). Требуется определить координаты второй точки В(х2, у2). Согласно рисунку,х2 – х1 =Δх; у2 – у1 = Δу.
Слайд 17Разности Δх и Δу координат точек последующей и предыдущей называют
приращениями координат. Из прямоугольного треугольника АВС имеем
Δх = dcosα; Δу
= dsiпα.Знаки Δх и Δу зависят от знаков cosα и sinα (по таблице).
Слайд 18С помощью румбов Δх и Δу можно вычислить по следуюшим
формулам: Δ х = dcos r; Δ у = dsin
r. Тогда искомые координаты точки В будут следующими: х2 = х1+ Δх; у1 = у2 + Δу.
Слайд 19Обратная задача. По данным координатам точек А и В найти
горизонтальное проложение d и дирек ционный угол α.
Из прямоугольного треугольника
АВС имеемtgα = Δу/Δх;
d = Δ x/cos α = Δ y/sin α.
