Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные понятия алгебры логики. Логические выражения и логические операции
Содержание
- 1. Основные понятия алгебры логики. Логические выражения и логические операции
- 2. Логика и компьютерДвоичное кодирование – все виды
- 3. ЛОГИКАНАУКА О ФОРМАХ И СПОСОБАХ МЫШЛЕНИЯ
- 4. МЫШЛЕНИЕ осуществляется через: Понятия Высказывания Умозаключения
- 5. ПОНЯТИЕ форма мышления, которая выделяет существенные признаки
- 6. УМОЗАКЛЮЧЕНИЕформа мышления, с помощью которой из одного
- 7. ВЫСКАЗЫВАНИЕформулировка своего понимания окружающего мира (повествовательное предложение
- 8. ВЫСКАЗЫВАНИЕ ИСТИННОЕ ЛОЖНОЕ
- 9. 1.2. ВысказываниеВопросительные и побудительные предложения не являются
- 10. Высказывание или нет?Сейчас идет дождь.Жирафы летят на
- 11. 2. Алгебра высказываний Алгебра высказываний служит для определения истинности или ложности составных высказываний.Основные понятия:логическая переменнаялогическая функциялогическая операция
- 12. Логическая переменнаяПростое высказывание, содержащее только одну мысль.Ее
- 13. Логическая функцияСоставное высказывание, которое содержит несколько простых
- 14. Обозначение высказыванийA – Сейчас идет дождь.B –
- 15. Логические операции2.1. Логическое умножение (конъюнкция)2.2. Логическое сложение
- 16. Правила выполнения логической операции отражаются в таблице
- 17. Круги Эйлера — геометрическая схема, с помощью которой
- 18. 2.1. Логическое умножение (конъюнкция)Объединение двух (или нескольких)
- 19. 2.2. Логическое сложение (дизъюнкция)Объединение двух (или нескольких)
- 20. 2.3. Логическое отрицание (инверсия)Присоединение частицы «не» к
- 21. 2.4. Логическое следование (импликация)Соответствует обороту Если…, то…Обозначение
- 22. 2.5. Логическое равенство (эквивалентность)Эквивалентность образуется соединением двух
- 23. Импликацию можно выразить через дизъюнкцию и отрицание:А В
- 24. ЗакреплениеПустьА=«Ане нравятся уроки математики», аВ=«Ане нравятся уроки
- 25. Определите истинность составного высказывания: (А&В) & (CvD),
- 26. 1. Какое из приведённых названий животных удовлетворяет
- 27. 2. Для какого имени ложно высказывание:Первая буква
- 28. 3. Какие из приведённых имён удовлетворяет
- 29. Для какого названия жука истинно высказывание:Вторая буква
- 30. Имеется запрос к поисковому серверу: newяблоки |
- 31. В таблице приведены запросы к поисковому серверу.
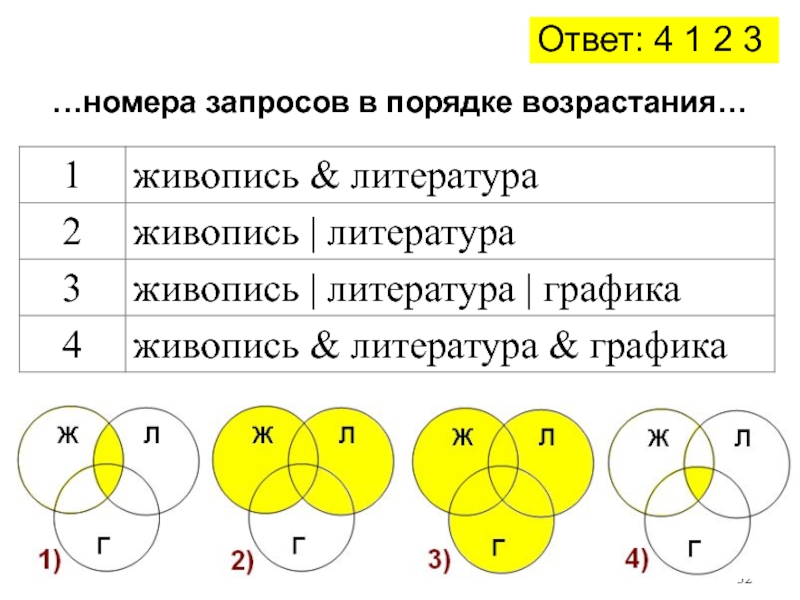
- 32. …номера запросов в порядке возрастания…Ответ: 4 1 2 3
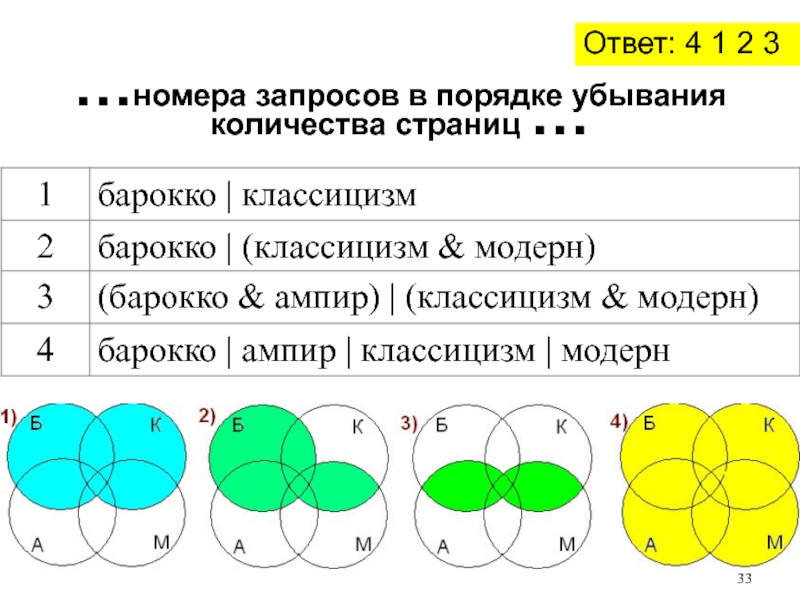
- 33. Ответ: 4 1 2 3…номера запросов в порядке убывания количества страниц …
- 34. Если составное высказывание (логическую функцию) выразить в
- 35. 3. Логические выражения и таблицы истинности Логическое
- 36. Порядок выполнения логических операций:Действия в скобкахИнверсияКонъюнкцияДизъюнкция ИмпликацияЭквивалентность
- 37. ПРИМЕР: Записать в виде логического выражения следующее
- 38. 4. Построение таблицы истинностиОпределить количество строк в
- 39. А V A & Bn (число переменных)
- 40. Пример. Для формулы A∧ (B ∨ C ) построить таблицу
- 41. Построение таблицы истинности для Количество строк таблицы
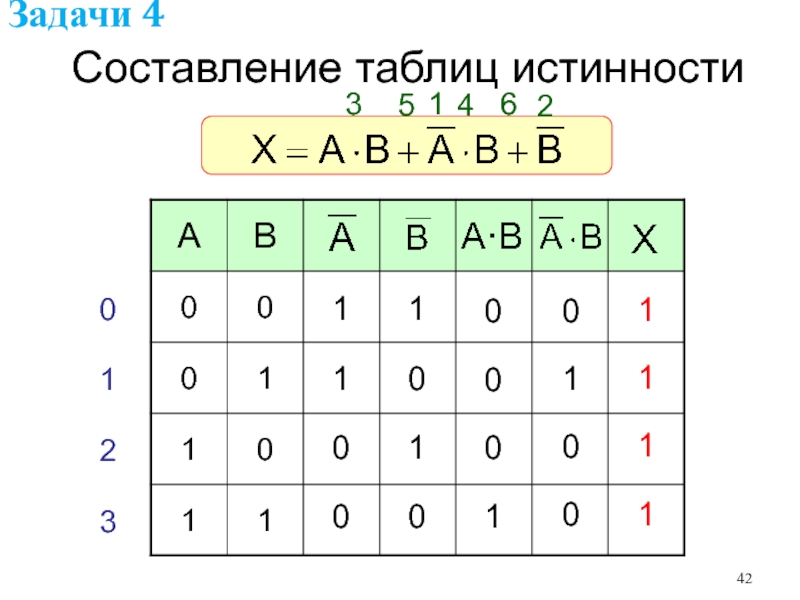
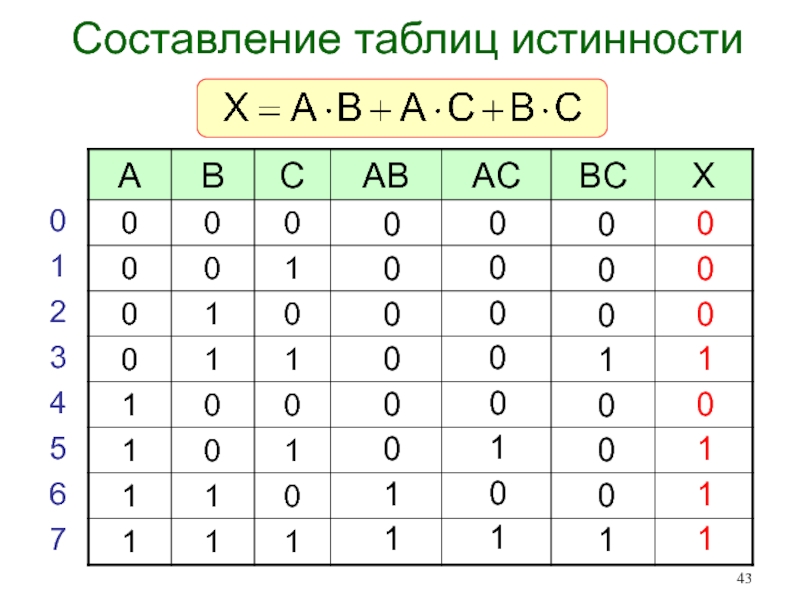
- 42. 123456Составление таблиц истинностиЗадачи 4
- 43. Составление таблиц истинности
- 44. Равносильные логические выраженияРавносильные логические выражения - это
- 45. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1A→B
AvB
A&B
Основные понятия алгебры логики. Логические выражения и логические операции
Джордж Буль
Слайд 2Логика и компьютер
Двоичное кодирование – все виды информации кодируются с
помощью 0 и 1.
Задача – разработать оптимальные правила обработки таких
данных.Почему «логика»? Результат выполнения операции можно представить как истинность (1) или ложность (0) некоторого высказывания.
Джордж Буль разработал основы алгебры, в которой используются только 0 и 1 (алгебра логики, булева алгебра).
Слайд 5ПОНЯТИЕ
форма мышления, которая выделяет существенные признаки предмета или класса
предметов, позволяющие отличать их друг от друга
(Пример: Прямоугольник - геометрическая
фигура у которой все углы прямые и противоположные стороны равны)Слайд 6УМОЗАКЛЮЧЕНИЕ
форма мышления, с помощью которой из одного или нескольких суждений
может быть получено новое суждение
(знание или вывод)
(Пример: любая теорема)
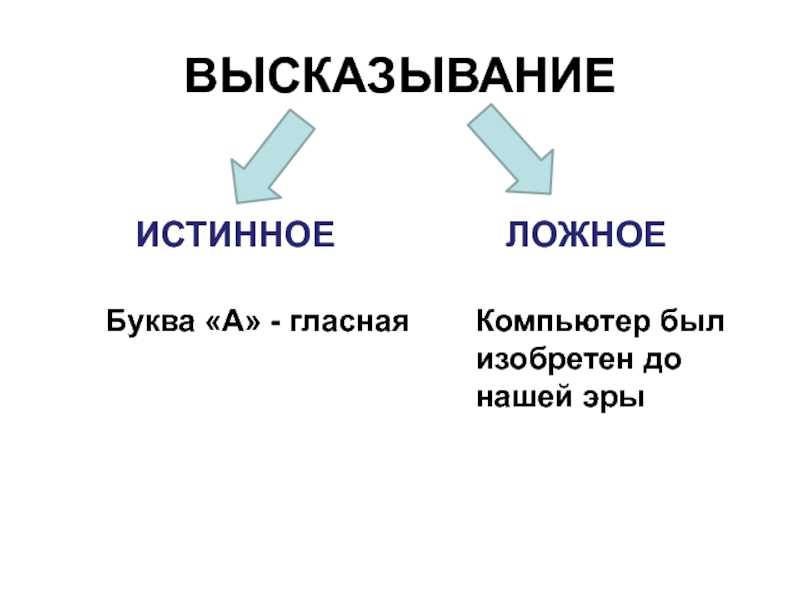
Слайд 7ВЫСКАЗЫВАНИЕ
формулировка своего понимания окружающего мира (повествовательное предложение в котором что-либо
утверждается или отрицается)
(Пример: Париж – столица Франции)
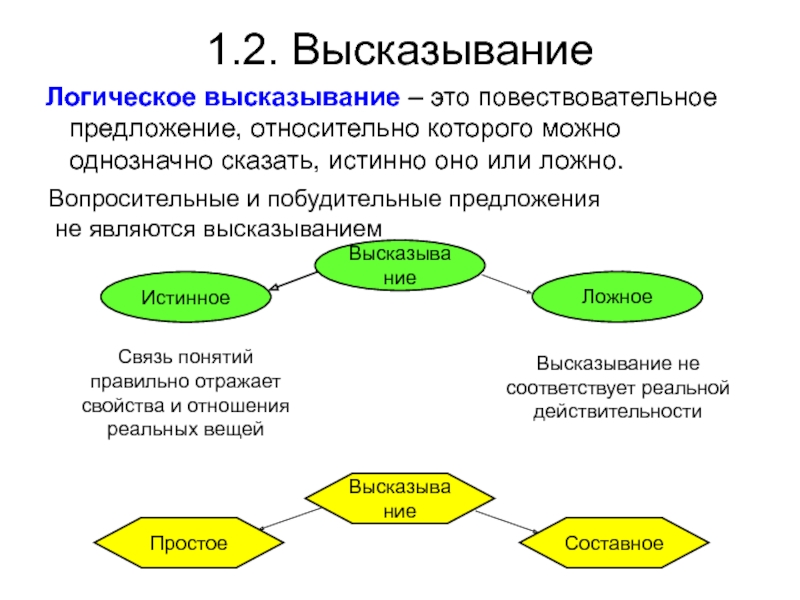
Слайд 91.2. Высказывание
Вопросительные и побудительные предложения
не являются высказыванием
Высказывание
Истинное
Ложное
Связь понятий правильно
отражает свойства и отношения реальных вещей
Высказывание не соответствует реальной действительности
Высказывание
Простое
Составное
Логическое
высказывание – это повествовательное предложение, относительно которого можно однозначно сказать, истинно оно или ложно.Слайд 10Высказывание или нет?
Сейчас идет дождь.
Жирафы летят на север.
История – интересный
предмет.
У квадрата – 10 сторон и все разные.
Красиво!
В городе N
живут 2 миллиона человек.Который час?
Слайд 112. Алгебра высказываний
Алгебра высказываний служит для определения истинности или ложности
составных высказываний.
Основные понятия:
логическая переменная
логическая функция
логическая операция
Слайд 12Логическая переменная
Простое высказывание, содержащее только одну мысль.
Ее символическое обозначение –
латинская буква (А, Х, Y и т.д.).
Значением логической переменной могут
быть только константы ИСТИНА и ЛОЖЬ (1 и 0).A – Сейчас идет дождь.
B – Форточка открыта.
Слайд 13Логическая функция
Составное высказывание, которое содержит несколько простых мыслей, соединенных между
собой с помощью логических операций.
Ее символическое обозначение –
F(A, B,..).
Слайд 14Обозначение высказываний
A – Сейчас идет дождь.
B – Форточка открыта.
простые высказывания
(элементарные)
Составные высказывания строятся из простых с помощью логических связок (операций)
«и», «или», «не», «если … то», «тогда и только тогда» и др. A и B
A или не B
если A, то B
A тогда и только
тогда, когда B
Сейчас идет дождь и открыта форточка.
Сейчас идет дождь или форточка закрыта.
Если сейчас идет дождь, то форточка открыта.
Дождь идет тогда и только тогда, когда открыта форточка.
Слайд 15Логические операции
2.1. Логическое умножение (конъюнкция)
2.2. Логическое сложение (дизъюнкция)
2.3. Логическое отрицание
(инверсия)
2.4. Логическое следование (импликация)
2.5. Логическое равенство (эквивалентность)
Слайд 16 Правила выполнения логической операции отражаются в таблице истинности.
Все операции алгебры
логики определяются таблицами истинности значений.
Таблица истинности определяет результат выполнения
операций для всех возможных логических значений исходных высказываний.
Таблица истинности логического выражения –
это таблица, где в левой части записываются все возможные комбинации значений исходных данных, а в правой – значение выражения для каждой комбинации.
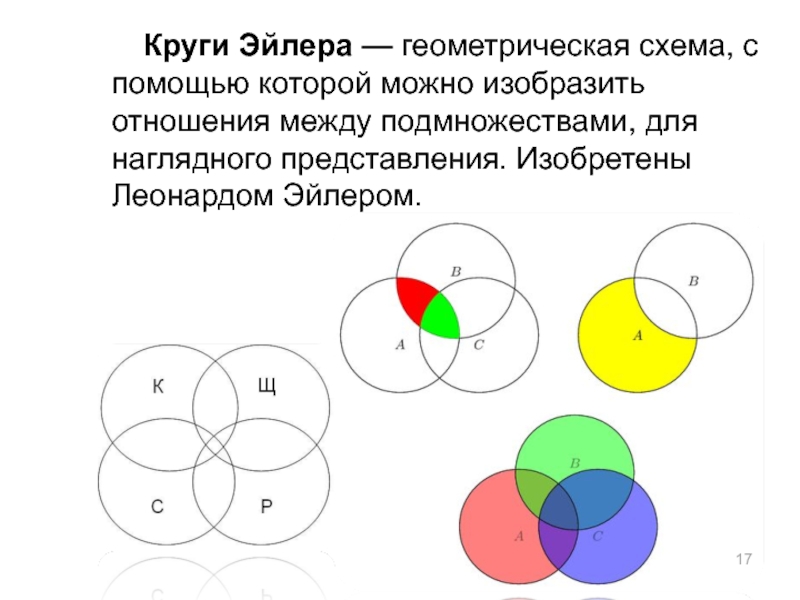
Слайд 17Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения
между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером.
Слайд 182.1. Логическое умножение (конъюнкция)
Объединение двух (или нескольких) высказываний в одно
с помощью союза «и».
Например: Сейчас идет дождь и открыта
форточка.Составное высказывание истинно только тогда, когда истинны оба простых высказывания.
Соответствует союзу И
Обозначение &, , , И.
Таблица истинности
A
B
А&В
Графическое представление
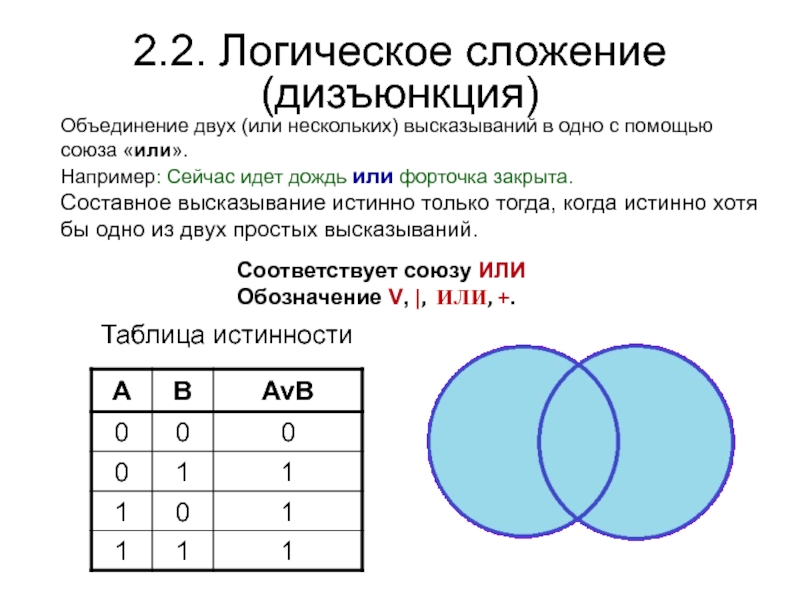
Слайд 192.2. Логическое сложение
(дизъюнкция)
Объединение двух (или нескольких) высказываний в одно с
помощью союза «или».
Например: Сейчас идет дождь или форточка закрыта.
Составное высказывание
истинно только тогда, когда истинно хотя бы одно из двух простых высказываний.Соответствует союзу ИЛИ
Обозначение V, |, ИЛИ, +.
Таблица истинности
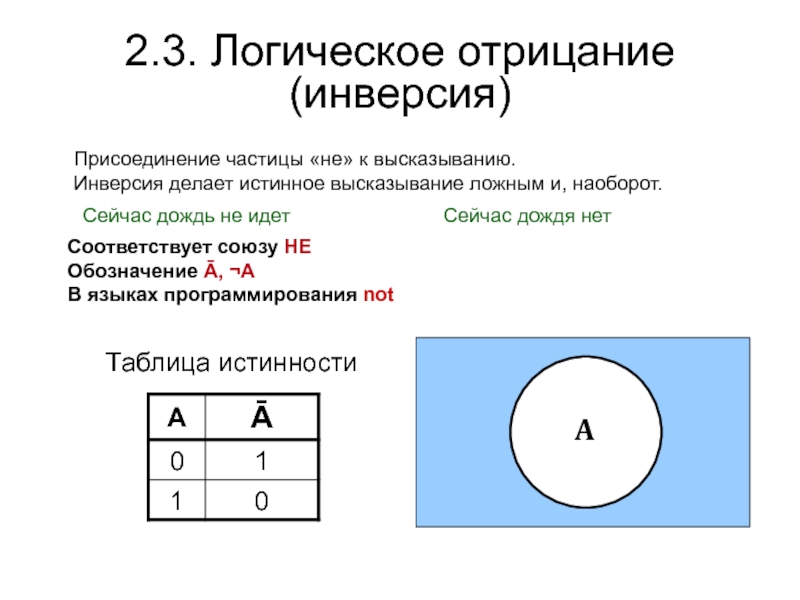
Слайд 202.3. Логическое отрицание
(инверсия)
Присоединение частицы «не» к высказыванию.
Инверсия делает истинное высказывание
ложным и, наоборот.
Соответствует союзу НЕ
Обозначение Ā, ¬А
В языках программирования not
Таблица
истинностиA
Сейчас дождя нет
Сейчас дождь не идет
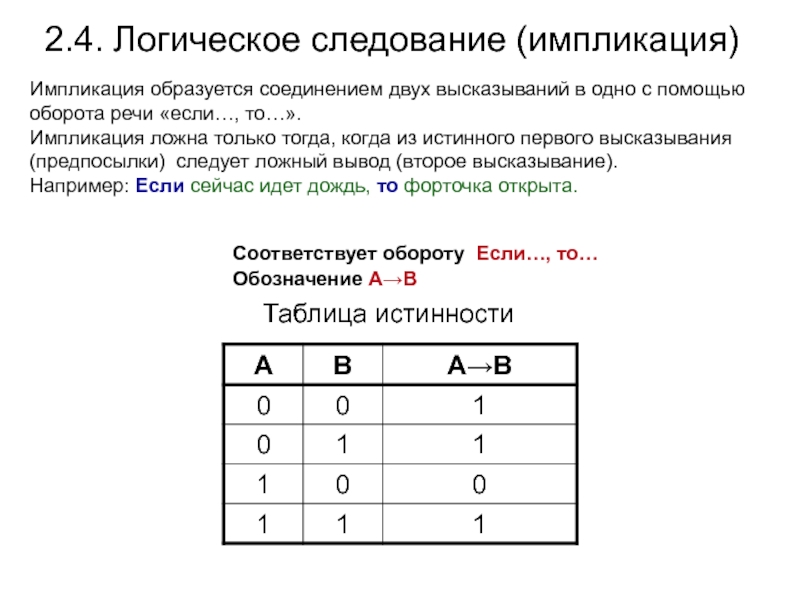
Слайд 212.4. Логическое следование (импликация)
Соответствует обороту Если…, то…
Обозначение А→В
Импликация образуется соединением
двух высказываний в одно с помощью оборота речи «если…, то…».
Импликация
ложна только тогда, когда из истинного первого высказывания(предпосылки) следует ложный вывод (второе высказывание).Например: Если сейчас идет дождь, то форточка открыта.
Таблица истинности
Слайд 222.5. Логическое равенство
(эквивалентность)
Эквивалентность образуется соединением двух высказываний в одно с
помощью оборота речи «… тогда и только тогда, когда …».
Составное
высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.Таблица истинности
Соответствует обороту тогда и только тогда, когда …
Обозначение А≡В, А~B
Например: Дождь идет тогда и только тогда, когда открыта форточка.
Слайд 23Импликацию можно выразить через дизъюнкцию и отрицание:
А В =A v В.
Эквиваленцию можно
выразить через отрицание, дизъюнкцию и
конъюнкцию: А В = ( A v В) . (B
v А).Слайд 24Закрепление
Пусть
А=«Ане нравятся уроки математики», а
В=«Ане нравятся уроки химии». Выразите следующие
формулы на обычном языке.
А&В
АvB (А&В)А&В АvB (АvB)
А&В АvB (А&В)
Задачи 1
Слайд 25Определите истинность составного высказывания:
(А&В) & (CvD), состоящего из простых
высказываний:
А = {Принтер – устройство вывода информации},
В =
{Процессор – устройство хранения информации}, С = {Монитор – устройство вывода информации},
D = {Клавиатура – устройство обработки информации}.
Сначала на основании знания устройства компьютера устанавливаем истинность простых высказываний:
А = 1, В = 0, С = 1, D = 0.
Определим теперь истинность составного высказывания, используя таблицы истинности логических операций:
( 1 & 0 ) &(1 v 0) = (0 & 1) & (1 v 0) = 0
Составное высказывание ложно.
Слайд 26
1. Какое из приведённых названий животных удовлетворяет логическому условию:
В слове
5 букв Четвёртая буква гласная?
Ответ: 3
Задачи 2
1 0
0
0
1 1
1 0
1 * 0
=
=
=
=
0 * 0
1 * 1
1 * 0
=
=
=
=
0
0
0
1
Слайд 272. Для какого имени ложно высказывание:
Первая буква гласная Четвёртая
буква согласная?
1) Петр
2) Алексей
3) Наталья
4) Елена
Ответ: 3
Слайд 283. Какие из приведённых имён
удовлетворяет логическому условию:
Первая буква гласная
Четвёртая буква согласная В слове 4 буквы?
1) Сергей
2)
Вадим3) Антон
4) Илья
5) Арина
Ответ: 4, 5
Слайд 29Для какого названия жука истинно высказывание:
Вторая буква согласная Четвёртая
буква гласная?
1) короед
2) усач
3) скрипун
4) плоскоход
new
Ответ: 3
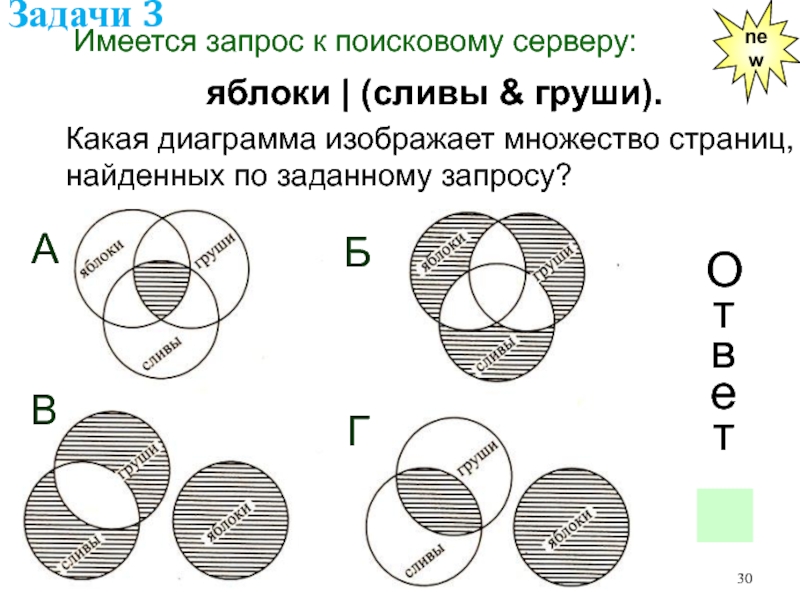
Слайд 30Имеется запрос к поисковому серверу:
new
яблоки | (сливы & груши).
Какая
диаграмма изображает множество страниц, найденных по заданному запросу?
Ответ
Г
A
В
Б
Г
Задачи 3
Слайд 31В таблице приведены запросы к поисковому серверу. Расположите номера запросов
в порядке возрастания количества страниц, которые найдёт поисковый сервер по
каждому запросу.Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» − &.
Слайд 34Если составное высказывание (логическую функцию) выразить в виде формулы, в
которую войдут логические переменные и знаки логических операций, то получится
ЛОГИЧЕСКОЕ ВЫРАЖЕНИЕ
истина ложь
Слайд 353. Логические выражения и таблицы истинности
Логическое выражение – формула,
в которую входят логические переменные и знаки логических операций.
Пример:
Для логического
выражения можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений простых высказываний.Порядок выполнения логических операций:
Действия в скобках.
Инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность.
Слайд 36Порядок выполнения логических операций:
Действия в скобках
Инверсия
Конъюнкция
Дизъюнкция
Импликация
Эквивалентность
Слайд 37ПРИМЕР: Записать в виде логического выражения следующее высказывание: «Летом Петя
поедет в деревню и, если будет хорошая погода, то он
пойдет на рыбалку»Это составное высказывание состоит из простых высказываний:
А = «Петя поедет в деревню»
В = «Будет хорошая погода»
С = «Он пойдет на рыбалку»
Записываем высказывание в виде логического выражения, учитывая порядок действий
F = A ^ (B → C)
Слайд 384. Построение таблицы истинности
Определить количество строк в таблице по формуле
2n, где n – количество логических переменных.
Определить количество столбцов таблицы:
количество логических переменных + количество логических операций.Построить таблицу истинности, обозначить столбцы, внести всевозможные наборы исходных данных логических переменных.
Заполнить таблицу истинности, выполняя базовые логические операции в необходимой последовательности.
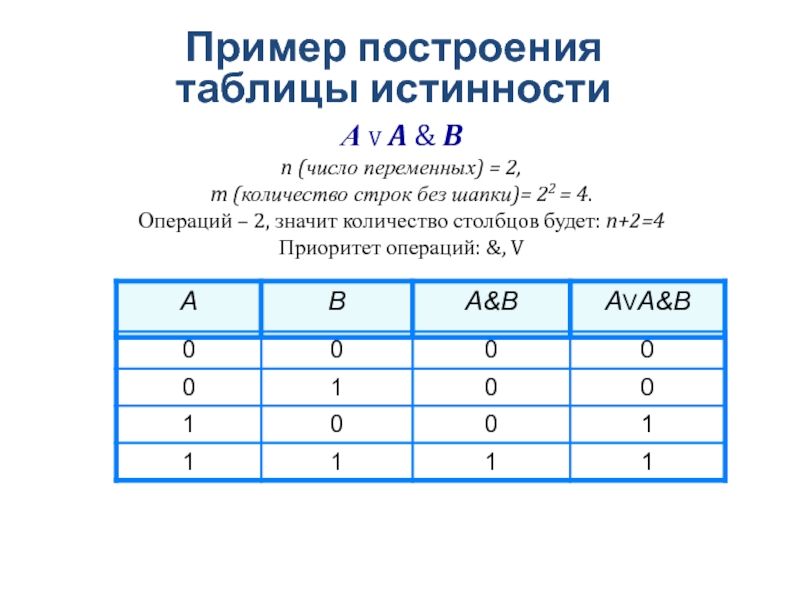
Слайд 39А V A & B
n (число переменных) = 2,
m
(количество строк без шапки)= 22 = 4.
Операций – 2, значит
количество столбцов будет: n+2=4 Приоритет операций: &, V
Пример построения
таблицы истинности
Слайд 40Пример. Для формулы A∧ (B ∨ C ) построить таблицу истинности алгебраически и
с использованием электронных таблиц. Количество логических переменных 3, следовательно, количество строк
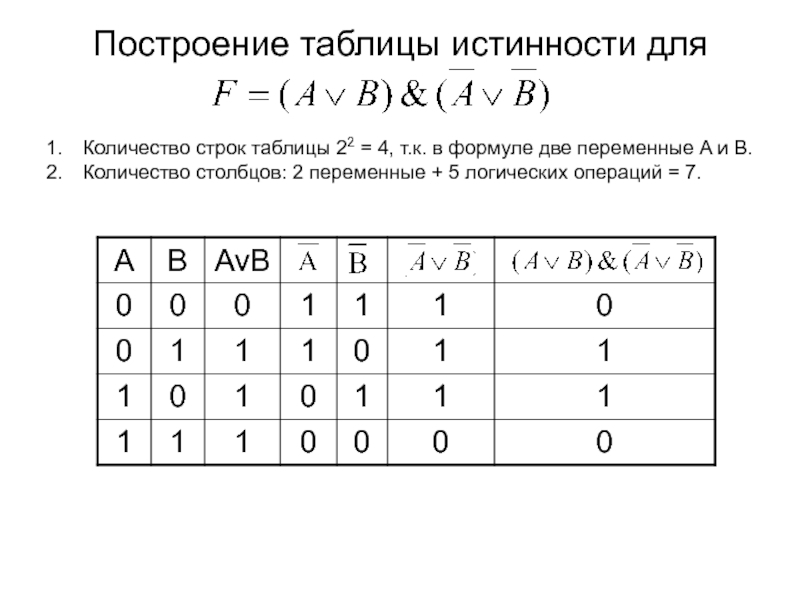
в таблице истинности должно быть 23 = 8. Количество логических операций в формуле 2, следовательно, количество столбцов в таблице истинности должно быть 3 + 2 = 5.Слайд 41Построение таблицы истинности для
Количество строк таблицы 22 = 4,
т.к. в формуле две переменные A и B.
Количество столбцов: 2
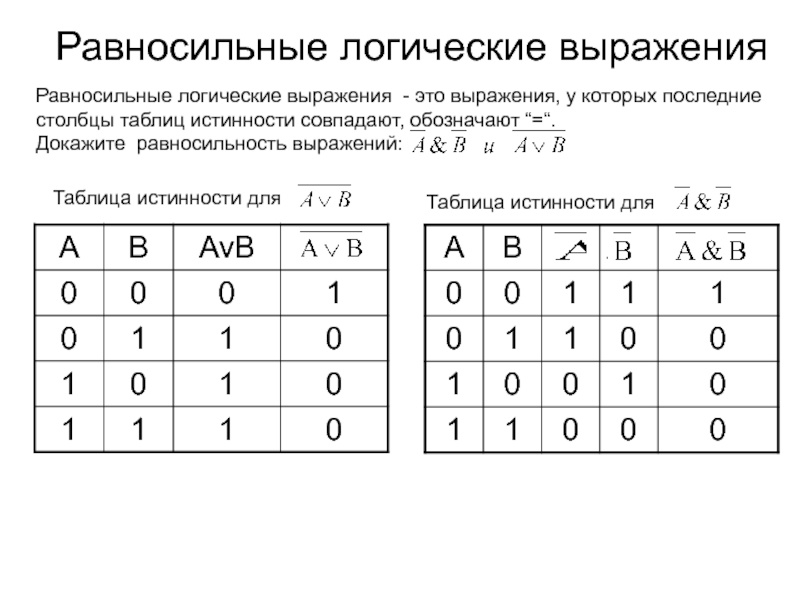
переменные + 5 логических операций = 7.Слайд 44Равносильные логические выражения
Равносильные логические выражения - это выражения, у которых
последние столбцы таблиц истинности совпадают, обозначают “=“.
Докажите равносильность выражений:
Таблица истинности
для Таблица истинности для