Слайд 1Основные понятия систем счисления
Слайд 2Система счисления – это символический метод записи чисел, представление чисел с помощью письменных
знаков.
Запись чисел по правилам определенной системы счисления – это способ
кодирования чисел.
От способа кодирования зависит размер кода, т.е. количество цифр в записи числа, а также правила выполнения вычислений.
Слайд 3Системы счисления
Системы счисления:
Двоичная
Восьмеричная
Десятичная
Шестнадцатеричная и др.
Виды систем счисления:
Позиционные (перечисленные выше)
Непозиционные (древнеегипетские
системы счисления)
Слайд 4Позиционные системы счисления. Основные понятия
Цифра – символ, используемый для записи
чисел.
Алфавит системы счисления – совокупность всех цифр.
Размерность алфавита – количество
цифр в алфавите.
Слайд 5Основные понятия
Каждая позиция в записи числа называется разрядом числа. Разряды
нумеруются в целой части числа положительными целыми числами, начиная с
нуля, в дробной части – отрицательными числами, начиная с -1:
Разряды: 3 2 1 0 -1-2
Число: 6248,54
Слайд 6Основные понятия
В записи многозначного числа цифры, стоящие в разных позициях,
имеют разные веса.
Например, десятичное число 325: тройка означает три сотни,
двойка – два десятка, пятерка – пять единиц.
Развернутая запись числа:
325 = 3*100 + 2*10 + 5*1 = 3*102 + 2*101 + 5*100
Развернутая форма записи числа – число записывается в виде суммы, в которой каждое слагаемое – это цифра, умноженная на свой вес.
Слайд 7Основные понятия
Основание системы счисления – размерность алфавита.
Основание десятичной системы счисления?
Наименьшее
основание для позиционных систем счисления является 2 (двоичная система счисления).
Основанием
традиционной системы счисления может быть любой натуральное число, начиная с двух, а базис – бесконечный в обе стороны ряд целых степеней основания.
Базис 10сс: … 104, 103, 102, 101, 100, 10-1, 10-2, 10-3, 10-4 …
Базис 2сс: … 26, 25, 24, 23, 22, 21, 20, 2-1, 2-2, 2-3, 2-4, 2-5, 2-6 …
Слайд 8Примеры позиционных систем счисления и их алфавитов:
При записи недесятичного числа
принято указывать его основание. Например, 1325 – число в пятеричной
системе счисления.
Слайд 9Правило
В любой позиционной системе счисления число, количественно равное ее основанию,
записывается как 10. при этом только в десятичной системе счисления
оно читается как «десять». Во все других следует читать как «один, ноль».
Например, 102 = 2, 103 = 3, 108 = 8, 1016 = 16 и т.д.
Слайд 10Задача
Перевести число 2011,13 в десятичную систему счисления.
Решение
Разложим данное число по
базису троичной системы счисления, т.е. запишем его в развернутой форме
и вычислим полученное выражение по правилам десятичной арифметики:
Слайд 11Задача
Шестнадцатеричное число 2AF,8C16 перевести в десятичную систему счисления.
Решение
Разложим данное число
по базису шестнадцатеричной системы счисления, т.е. запишем его в развернутой
форме и вычислим полученное выражение по правилам десятичной арифметики. В записи разложения цифры, обозначаемые буквами, заменяются на их эквиваленты в десятичной системе.
2AF,8C16 = 2*162 + 10*161 + 15*160 + 8*16-1 + 12*16-2 =
= 512 + 160 + 15 + ½ + 3/64 = 687,546875
Слайд 12Задание
Перевести указанные числа в десятичную систему счисления:
1012
111012
1010102
Слайд 13Перевод десятичных чисел в другие системы счисления
Правило перевода целой части
числа состоит из следующих этапов:
число N делится на новое основание р;
полученный остаток обводиться;
целая часть
полученного частного снова делится на р;
опять обводиться полученный остаток и т. д. до тех пор, пока целая часть частного не окажется меньше, чем основание системы счисления р.
результат формируется путем последовательной записи слева направо обведенных цифр в порядке, обратном их получению.
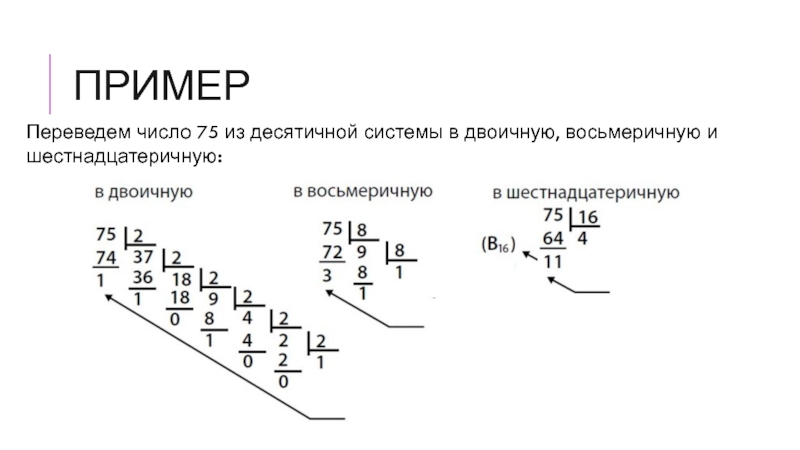
Слайд 14Пример
Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
Слайд 15Задание
Перевести указанные числа в двоичную систему счисления:
17
68
Слайд 16перевод дробной части числа
Правило перевода дробной части числа состоит из следующих
этапов:
дробная часть числа умножается на основание р;
записывается цифра результата, переносимая в
целую часть;
оставшаяся дробная часть числа умножается на основание р;
снова фиксируется цифра результата, переносимая в целую часть, и т. д. до тех пор, пока в дробной части не будет получен ноль или достигнута требуемая точность, например 5 знаков после запятой.
Результат формируется в виде последовательной записи зафиксированных цифр переносов в целую часть в том порядке, в котором они были получены.
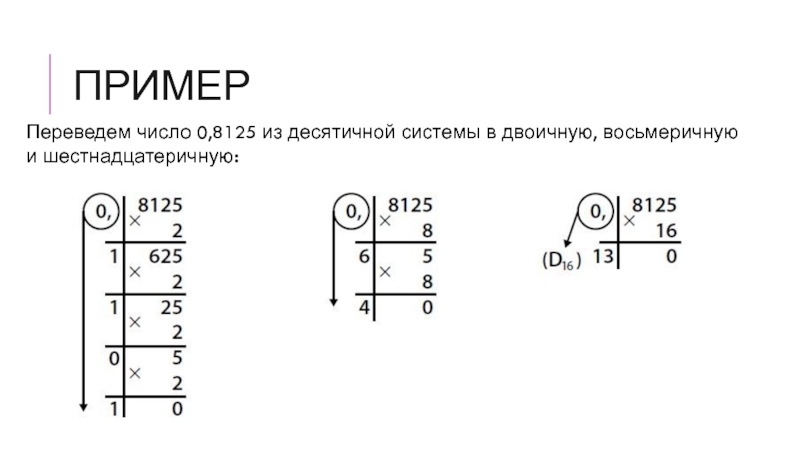
Слайд 17Пример
Переведем число 0,8125 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
Слайд 18Задание
Перевести указанные числа в двоичную систему счисления:
0,32
0,127
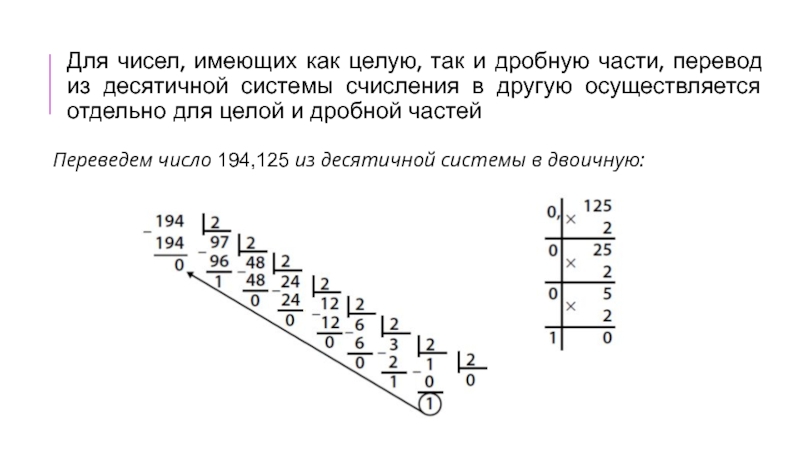
Слайд 19Для чисел, имеющих как целую, так и дробную части, перевод
из десятичной системы счисления в другую осуществляется отдельно для целой
и дробной частей
Переведем число 194,125 из десятичной системы в двоичную:
Слайд 20Задание
Перевести указанные числа в двоичную систему счисления:
23,35
71,123
Слайд 21Смешанные системы счисления
Способ записи чисел, при котором числа из позиционной
системы счисления с основанием Q записываются с помощью цифр системы
счисления с основанием P, называется смешанной P-Q-ичной системой счисления.
Слайд 22Двоично-восьмеричная система счисления
Решение:
Делим данное двоичное число на триады: 010 101
010 0012
Каждой триаде ищем соответствие по таблице:
010 101 010
0012
2 5 2 1
3. Записываем результат: 101010100012 = 25218
Перевести число 101010100012 в восьмеричную систему счисления.
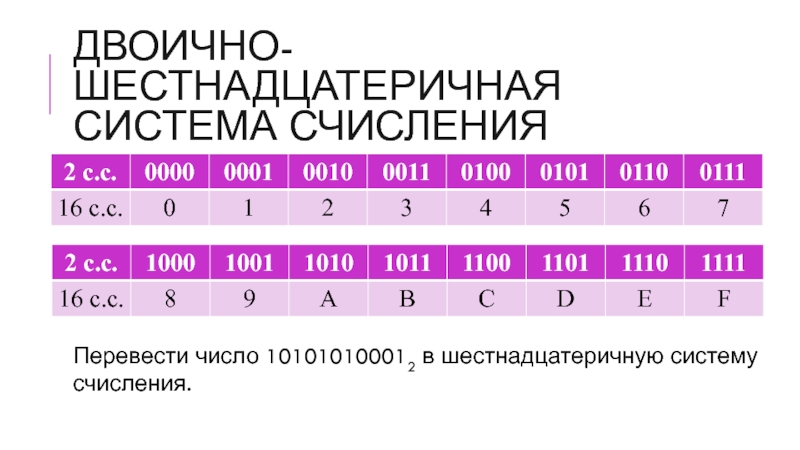
Слайд 23Двоично-шестнадцатеричная система счисления
Перевести число 101010100012 в шестнадцатеричную систему счисления.
Слайд 24Двоично-шестнадцатеричная система счисления
Решение:
Делим данное двоичное число на тетрады: 0101 0101
00012
Каждой тетраде ищем соответствие по таблице:
0101 0101 00012
5 5 1
3. Записываем результат: 101010100012 = 55116
Перевести число 101010100012 в восьмеричную систему счисления.
Слайд 25Задание
Перевести указанные числа из двоичной системы счисления в восьмеричную и
шестнадцатеричную:
1000112
101101110112
Перевести указанные числа в двоичную систему счисления:
5A16
578