Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ОСНОВЫ МЕХАНИЧЕСКОЙ И МОЛЕКУЛЯРНОЙ ФИЗИКИ
Содержание
- 1. ОСНОВЫ МЕХАНИЧЕСКОЙ И МОЛЕКУЛЯРНОЙ ФИЗИКИ
- 2. Литература1. Курбачев, Ю. Ф. Физика : учебное
- 3. Раздел 1. Физические основы механики
- 4. Общие понятия физики Физика - наука,
- 5. Общие понятия физикиМатерия - объективная реальность, которую
- 6. Слайд 6
- 7. Механика подразделяется
- 8. Кинематика Кинематика изучает движение
- 9. Кинематика Механическим движением называют изменение с течением
- 10. Кинематика Поступательным движением называется движение, при
- 11. Основные кинематические понятия
- 12. Кинематика Материальная точка - это тело, обладающее
- 13. Кинематика Абсолютно твердое тело − тело, деформацией
- 14. КинематикаСистемой отсчета называют тело отсчета, относительно
- 15. КинематикаВ декартовой системе координат положение точки определяется
- 16. Линия, описываемая в пространстве движущейся точкой, называется
- 17. Вектор перемещения и путь
- 18. СкоростьПусть в момент времени t тело находилось
- 19. СкоростьСкорость ( ) – векторная физическая величина,
- 20. СкоростьПуть, пройденный телом за конечный промежуток времени
- 21. СкоростьЕсли направление вектора скорости не изменяется, то
- 22. СкоростьВ случае неравномерного движения, пользуются скалярной величиной
- 23. УскорениеПусть в момент времени t тело находилось
- 24. УскорениеБыстрота изменения скорости по модулю и направлениюносит
- 25. УскорениеПри прямолинейном движении направление скоростиостается постоянным, поэтому
- 26. УскорениеИнтегрируя функцию скорости в пределах от 0
- 27. УскорениеЕсли скорость изменяется с течением времени произвольнымобразом,
- 28. При криволинейном движении вектор скорости
- 29. УскорениеТангенциальное ускорение характеризует быстроту изменения скорости по
- 30. 1) aτ = 0, an = 0
- 31. Кинематика вращательного движенияВращательным движением называют движение,при
- 32. Характеристики вращательного движенияУгловое перемещение (
- 33. Характеристики равномерного вращенияПериод вращения (Т) – время,
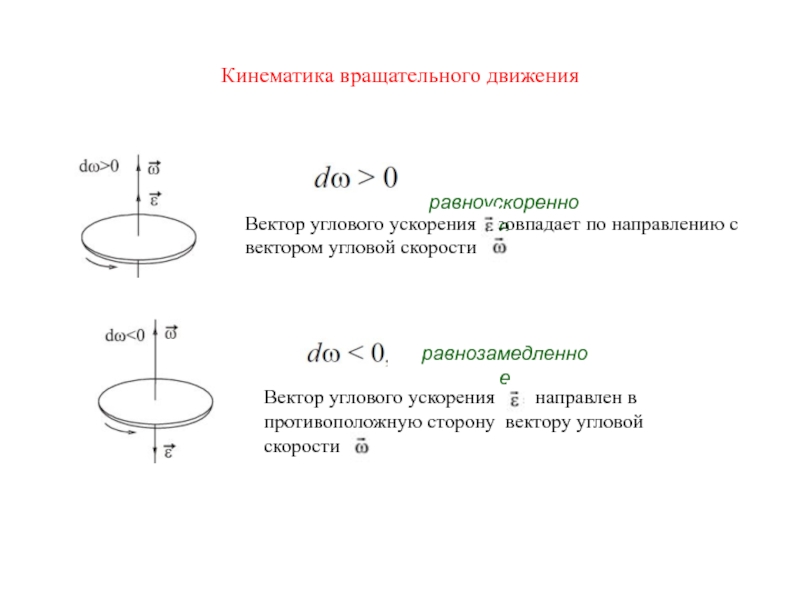
- 34. Кинематика вращательного движения равноускоренноеВектор углового ускорения
- 35. Кинематика вращательного движения
- 36. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ОСНОВЫ МЕХАНИЧЕСКОЙ И МОЛЕКУЛЯРНОЙ ФИЗИКИ
Старший преподаватель Гайсина Лилия Гаязовна
e-mail:
udgu_gaisina@mail.ru
Слайд 2Литература
1. Курбачев, Ю. Ф. Физика : учебное пособие / Ю.
Ф. Курбачев. — М. : Евразийский открытый институт, 2011. —
216 c. — ISBN 978-5-374-00523-3. — Текст : электронный // Электронно-библиотечная система IPR BOOKS : [сайт]. — URL: http://www.iprbookshop.ru/11106.html2. Михайлов, В. К. Физика : учебное пособие / В. К. Михайлов. — М. : Московский государственный строительный университет, ЭБС АСВ, 2013. — 120 c. — ISBN 978-5-7264-0679-4. — Текст : электронный // Электронно-библиотечная система IPR BOOKS : [сайт]. — URL: http://www.iprbookshop.ru/23753.html
3. Плешакова, Е. О. Физика. Механика : учебное пособие / Е. О. Плешакова. — Волгоград : Волгоградский институт бизнеса, Вузовское образование, 2008. — 142 c. — ISBN 2227-8397. — Текст : электронный // Электронно-библиотечная система IPR BOOKS : [сайт]. — URL: http://www.iprbookshop.ru/11356.html
4. Ташлыкова-Бушкевич, И. И. Физика. Часть 1. Механика. Молекулярная физика и термодинамика. Электричество и магнетизм : учебник / И. И. Ташлыкова-Бушкевич. — Минск : Вышэйшая школа, 2014. — 304 c. — ISBN 978-985-06-2505-2. — Текст : электронный // Электронно-библиотечная система IPR BOOKS : [сайт]. — URL: http://www.iprbookshop.ru/35562.html
5. Чакак, А. А. Физика. Краткий курс : учебное пособие для студентов очно-заочной формы обучения вузов, слушателей курсов повышения квалификации и профессиональной переподготовки специалистов, для студентов факультета дистанционных образовательных технологий / А. А. Чакак, С. Н. Летута. — Оренбург : Оренбургский государственный университет, ЭБС АСВ, 2011. — 541 c. — ISBN 2227-8397. — Текст : электронный // Электронно-библиотечная система IPR BOOKS : [сайт]. — URL: http://www.iprbookshop.ru/30092.htm
Слайд 4Общие понятия физики
Физика - наука, изучающая
простейшие и вместе с тем наиболее общие закономерности явлений природы,
свойства и строение материи и законы ее движенияСлайд 5Общие понятия физики
Материя -
объективная реальность, которую мы познаем с
помощью органов чувств и приборов
Движение -
всякое изменение вообще
Слайд 8
Кинематика
Кинематика изучает движение тел и
математически описывает различные виды
механического движения, не выясняя причин этого
движения.
Основная задача кинематики– определить
положение
тела в любой момент времени.Слайд 9Кинематика
Механическим движением называют изменение
с течением времен положения тела в
пространстве.
Основными видами механического движения
являются поступательное и вращательное
движения.
Слайд 10Кинематика
Поступательным движением называется движение, при котором любая прямая, связанная
с движущимся телом, остается параллельной самой себе.
При поступательном движении
все точки тела движутся одинаково, поэтому можно рассматривать движение тела независимо от его размеров и формы, как движение одной точки тела. Вращательным движением называют движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.
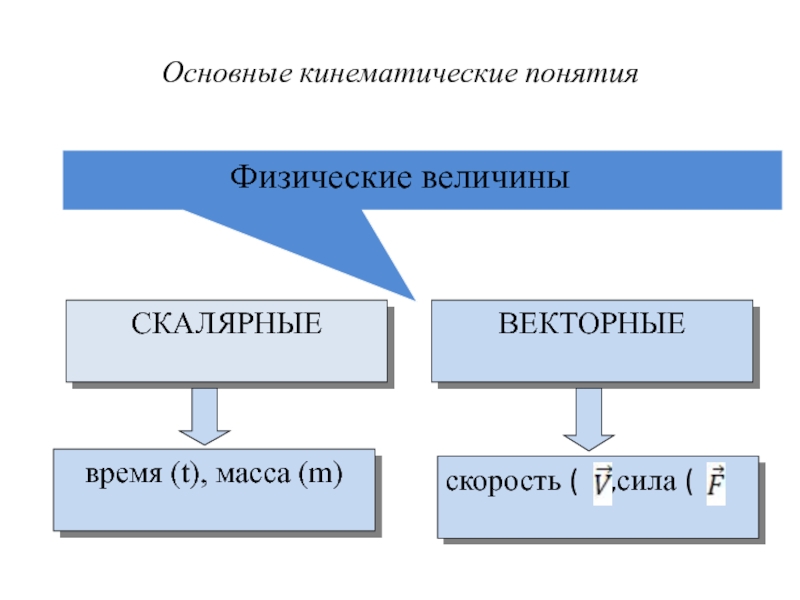
Слайд 11Основные кинематические понятия
Физические величины
СКАЛЯРНЫЕ
ВЕКТОРНЫЕ
время (t), масса (m)
скорость ( ) ,сила (
)Слайд 12Кинематика
Материальная точка - это тело, обладающее массой, размерами которого в
условиях рассматриваемой задачи можно пренебречь
ФИЗИЧЕСКАЯ МОДЕЛЬ
Слайд 13Кинематика
Абсолютно твердое тело − тело, деформацией которого в условиях данной
задачи можно пренебречь.
Абсолютно упругое тело − тело, которое после
прекращения внешнего силового воздействия полностью восстанавливает свои первоначальные размеры и форму. Абсолютно неупругое тело − тело, которое после прекращения внешнего силового воздействия полностью сохраняет деформированное состояние, вызванное этим воздействием.
Слайд 14Кинематика
Системой отсчета называют тело отсчета, относительно которого определяется положение
всех других тел, и связанные с этим телом часы.
Тело
отсчета – произвольно выбранное тело, относительно которого определяется положение других (движущихся )тел.Слайд 15Кинематика
В декартовой системе координат положение точки
определяется тремя координатами x,
y, z или радиус
вектором проведенным из начала отсчета в точку,
гденаходится тело.
Движение материальной точки можно описать тремя
скалярными уравнениями
x = x(t); y = y(t); z = z(t)
или векторным уравнением
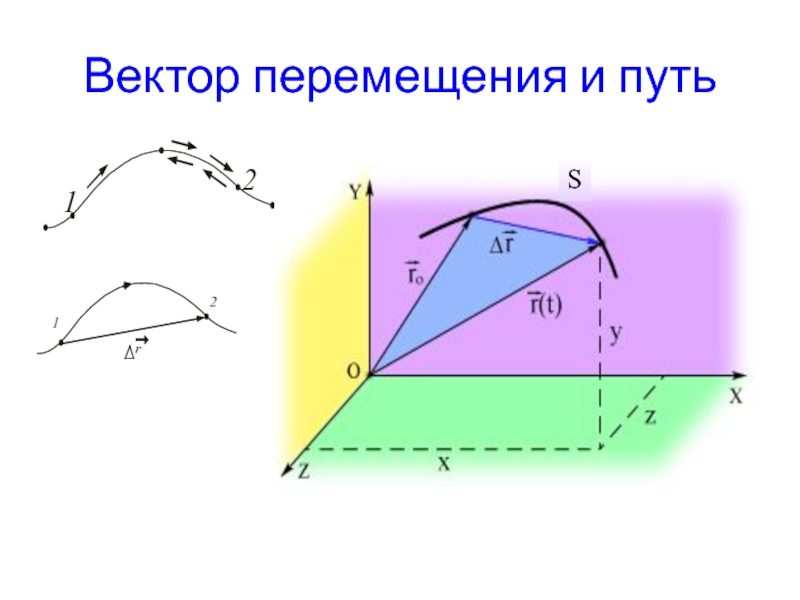
Слайд 16Линия, описываемая в пространстве движущейся точкой, называется траекторией.
Длина участка
траектории АВ, пройденного материальной точкой за время Δt, называется длиной
пути ΔsΔs = Δs(t) – скалярная функция времени
Вектор, проведенный из начального положения точки в положение ее в данный момент времени, называется перемещением ∆
В зависимости от формы траектории движение может быть прямолинейным или криволинейным.
в случае прямолинейного движения
Слайд 18Скорость
Пусть в момент времени t тело находилось в точке 1,
положение которой
задается радиус-вектором . За время Δt оно
совершило перемещение Δ и оказалось в точке 2.
Слайд 19Скорость
Скорость ( ) – векторная физическая величина,
характеризующая быстроту изменения
положения тела в
пространстве и равная первой производной радиус-вектора
по времени.
Вектор
скорости всегда направлен по касательной ктраектории в сторону движения.
Модуль скорости v определяется как производная пути по
времени:
Слайд 20Скорость
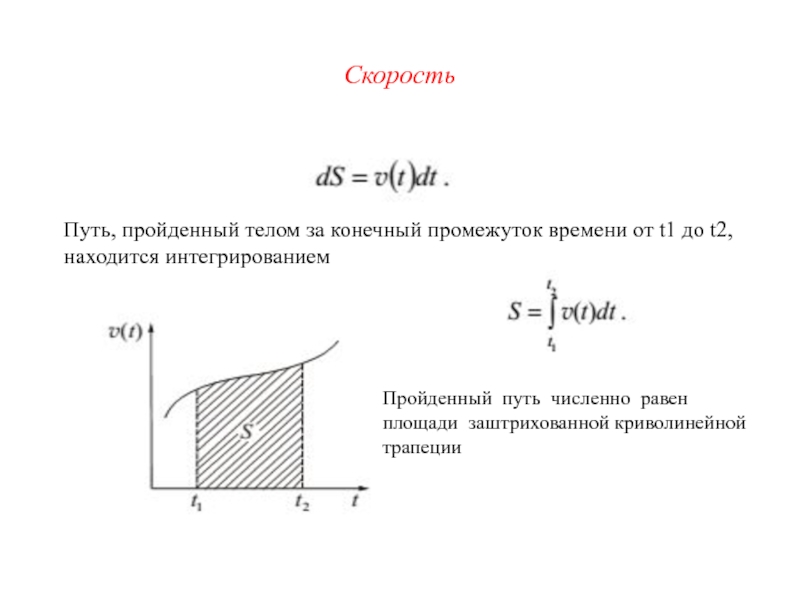
Путь, пройденный телом за конечный промежуток времени от t1 до
t2, находится интегрированием
Пройденный путь численно равен площади заштрихованной криволинейной трапеции
Слайд 21Скорость
Если направление вектора скорости не изменяется, то движение называется прямолинейным.
Если модуль скорости не изменяется с течением времени, то движение
называется равномерным.При равномерном движении скорость тела постоянна:
Слайд 22Скорость
В случае неравномерного движения, пользуются скалярной величиной
- средней скоростью неравномерного движения на данном участке за этот
промежуток времени:Слайд 23Ускорение
Пусть в момент времени t тело находилось в точке1, имея
скорость 1. Через время Δt оно переместилось в точку
2, приэтом его скорость стала равной 2
Приращение вектора скорости равно:
Слайд 24Ускорение
Быстрота изменения скорости по модулю и направлению
носит названия ускорения.
Ускорение (
) – это векторная физическая величина, характеризующая быстроту изменения вектора
скорости и равная производной вектора скорости по времени.Слайд 25Ускорение
При прямолинейном движении направление скорости
остается постоянным, поэтому вектор ускорения или
совпадает
с направлением скорости, или противоположен
ему.
Скорость движения в любой момент времени
будетопределяться соотношением:
V0 - начальная скорость тела, т.е. скорость в момент времени t=0;
± - равноускоренное или равнозамедленное движение соответственно.
Слайд 26Ускорение
Интегрируя функцию скорости в пределах от 0 до произвольного момент
времени t, найдем формулу для расчета пройденного пути
Слайд 27Ускорение
Если скорость изменяется с течением времени произвольным
образом, то величина, равная
отношению изменения
скорости Δv к промежутку времени Δt, в течение которого
изменялась
скорость, называется средним ускорением заэтот промежуток времени
Слайд 28
При криволинейном движении вектор скорости изменяет
свое направление. При
этом может изменяться и его
численное значение, т.е. модуль.
В этом случае
вектор ускорения удобно раскладывать на две составляющие:- тангенциальное (касательное) ускорение;
- нормальное (центростремительное) ускорение
Полное ускорение –геометрическая сумма тангенциальной и нормальной составляющих
Слайд 29Ускорение
Тангенциальное ускорение характеризует быстроту изменения скорости по величине и равно
первой производной модуля скорости по времени:
Нормальное (центростремительное) ускорение характеризует быстроту
изменения скорости по направлению и направлено по радиусу к центру кривизны траектории.Модуль полного ускорения равен:
Слайд 301) aτ = 0, an = 0 - прямолинейное равномерное
движение;
2) aτ = a = const, an = 0
- прямолинейное равнопеременнoе движение. 3) , аn = 0 - прямолинейное движение с переменным ускорением;
аτ = 0, аn = const.
При аτ = 0 скорость по модулю не изменяется, а изменяется по направлению
(движение по окружности).
Слайд 31Кинематика вращательного движения
Вращательным движением называют движение,
при котором все точки
тела движутся по
окружностям, центры которых лежат на одной
прямой, называемой осью
вращения.Слайд 32Характеристики вращательного движения
Угловое перемещение ( ) –
вектор, модуль которого равен углу поворота, выраженному в радианах.
Угловая скорость
( ) – векторная физическая величина, характеризующая быстроту вращения и равная первой производной углового перемещения по времени:Вращение с постоянной угловой скоростью называется равномерным
Слайд 33Характеристики равномерного вращения
Период вращения (Т) – время, в течение которого
совершается один полный оборот. За время, равное периоду, тело поворачивается
на угол 2π.Частота вращения(ν) – число оборотов за единицу времени
Угловое ускорение ( ) – векторная физическая величина, характеризующая быстроту изменения угловой скорости и равная первой производной угловой скорости по времени