Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы программирования Fortran, C++, D
Содержание
- 1. Основы программирования Fortran, C++, D
- 2. Занятие третье, 21 сентябряВычислительные объекты и операции Правила
- 3. Вопросы от 14 сентября:Концепция построения и особенности
- 4. Практика, 21 сентября, 2-3 пара Персональные компьютерыwww.equation.com
- 5. Algol-60Стандартные операции
- 6. Algol-6035 ключевых слов (standard Burroughs sub-language):alpha array
- 7. Fortran-4 Cтандартизированный язык машинных команд IBMFUNCTION,
- 8. Fortran-II (идея троичной логики)C AREA OF A
- 9. Программы – это операции на предопределенных типах
- 10. C, C++ – стандартные операции
- 11. C, C++ – стандартные операции
- 12. D (Ди) язык программированияA abstract alias align
- 13. D – язык программирования
- 14. D – язык программирования
- 15. D – язык программирования
- 16. D – язык программирования
- 17. D – язык программирования
- 18. D – язык программирования
- 19. D – язык программирования
- 20. OpenMP – параллельное исполнение команд в С#include
- 21. Язык D – Ver.2 / Tango (тень
- 22. Вопросы:Ключевые слова и зарезервированные идентификаторы языков программирования
- 23. Исчисление флюксий (анализ в конечных разностях)Все же,
- 24. Исчисление флюксийДифференцирование – поиск флюксий по Ньютону
- 25. Координатные системы отсчета ( абсолютные и локальные
- 26. Координатные системы отсчета ( абсолютные и локальные
- 27. Вычислительные объекты1) Скаляр – числовая величина, не
- 28. Координатные системы отсчета ( абсолютные и локальные
- 29. Координатные системы отсчета ( абсолютные и локальные
- 30. Координатные системы отсчета ( компьютерное представление )typedef
- 31. Исчисление векторов (определения тензорной математики)Литература... Н.Е.
- 32. Исчисление векторов (определения – вполне реальная альтернатива)Литература...
- 33. Исчисление векторов (операции сложения векторов)Операция сложения векторов,
- 34. Исчисление тензоров (геометрические определения) Базисные векторы локальной системы
- 35. Исчисление тензоров (геометрические преобразования)В пространственном исчислении (в
- 36. Объем базиса – детерминантИсчисление тензоров (интерпретация
- 37. Исчисление тензоров (интерпретация геометрических базисов)Координатные преобразования для
- 38. Исчисление тензоров (продолжение и замечания)В исчислении флюксий
- 39. Занятие третье, 21 сентября3++ Практические занятия … Рассмотрение
- 40. Четвертое занятие …Практика программирования в среде Windows.
- 41. Разделенные разности НьютонаЧисленное построение функции по дискретным
- 42. Разделенные разностиПроверка на совпадение значений функции в узловых точках:
- 43. Интерполирующие многочленыФорма Ньютона:Форма Лагранжа:схема спуска минимизирует количество вычислительных операций
- 44. Эффективный алгоритм интерполяции с заданным поведением функции
- 45. Практика, 14 сентября, 2-3 пара Персональные компьютерыwww.equation.com
- 46. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Основы
программирования
Fortran, C++, D
Санкт-Петербургский
государственный университет
фак. Прикладной математики – процессов управления
гр.
103 – прикладная математика и информатика
Объекты и операции. Занятие № 3 Храмушин Василий Николаевич – Khram@mail.ru, Khram@Russia.ru каф. компьютерного моделирования и многопроцессорных системСлайд 2Занятие третье, 21 сентября
Вычислительные объекты и операции
Правила формирования и вычисления
выражений в языке Си++. Все операции языка.
Выражения
Операция присваивания
Все операции языка
Си++ Арифметические операции
Операции сравнения
Логические операции
Битовые операции
Условная операция
Последовательность
Операции присваивания
Порядок вычисления выражений
Слайд 3Вопросы от 14 сентября:
Концепция построения и особенности реализации языков программирования
на примерах Fortran(57), Algol(58), В(69), C(72), C++(83), D(2001) и др;
Машинно-зависимые
типы данных
(стек, статика, куча), особенности их использования, скорость доступа и эффективность выполнения операций на линейном процессоре.Компиляция и интерпретация, достоинства в использовании и проблемы реализации формализованных и специальных языков программирования (декларативные алгоритмы и функциональные языки искусственного интеллекта)
Слайд 4Практика, 21 сентября, 2-3 пара
Персональные компьютеры
www.equation.com – Fortran, C++
dlang.org
– D-compiler (GDC или DigitalMars)
www.codeblocks.org –
среда разработкиwxdsgn.sourceforge.net – xWindow, Dev-C++
Классный компьютер
login: student101e
password: student101e \\ws101-operator\Shared folder
Слайд 6Algol-60
35 ключевых слов (standard Burroughs sub-language):
alpha array begin boolean comment
continue direct do double else end event false file for
format go if integer label list long own pointer procedure real step switch task then true until value while zip71 зарезервированный идентификатор
accept and attach by call case cause close deallocate define detach disable display div dump enable eql eqv exchange external fill forward geq gtr imp in interrupt is lb leq liberate line lock lss merge mod monitor mux neq no not on open or out picture process procure programdump rb read release replace reset resize rewind run scan seek set skip sort space swap thru times to wait when with write
Слайд 7Fortran-4
Cтандартизированный язык машинных команд IBM
FUNCTION, SUBROUTINE и ENTRY;
Блок
описания данных в прологе процедуры
BLOCK DATA для определения начальных значений;
INTEGER, REAL,
DOUBLE PRECISION, COMPLEX, LOGICAL;
(сохраняются в течение всего времени выполнения программы)IMPLICIT, COMMON, DIMENSION, EQUIVALENCE
Команды порядка исполнения программы
CALL, RETURN, PAUSE, STOP – управление прораммой;
оператор GOTO, назначаемый GOTO и вычисляемый GOTO
IF – логический и арифметический, DO и CONTINUE;
Пользовательский интерфейс - полноценный
ввод/вывод READ, WRITE, BACKSPACE, REWIND, ENDFILE;
строка интерпретатора ввода/вывода FORMAT
Слайд 8Fortran-II (идея троичной логики)
C AREA OF A TRIANGLE WITH A
STANDARD SQUARE ROOT FUNCTION
C INPUT - CARD READER UNIT 5,
INTEGER INPUTC OUTPUT - LINE PRINTER UNIT 6, REAL OUTPUT
C INPUT ERROR DISPLAY ERROR OUTPUT CODE 1 IN JOB CONTROL LISTING
READ INPUT TAPE 5, 501, IA, IB, IC
501 FORMAT (3I5)
C IA, IB, AND IC MAY NOT BE NEGATIVE
C FURTHERMORE, THE SUM OF TWO SIDES OF A TRIANGLE
C IS GREATER THAN THE THIRD SIDE, SO WE CHECK FOR THAT, TOO
IF (IA) 777, 777, 701
701 IF (IB) 777, 777, 702
702 IF (IC) 777, 777, 703
703 IF (IA+IB-IC) 777,777,704
704 IF (IA+IC-IB) 777,777,705
705 IF (IB+IC-IA) 777,777,799
777 STOP 1
C USING HERON'S FORMULA WE CALCULATE THE
C AREA OF THE TRIANGLE
799 S = FLOATF (IA + IB + IC) / 2.0
AREA = SQRT( S * (S - FLOATF(IA)) * (S - FLOATF(IB)) *
+ (S - FLOATF(IC)))
WRITE OUTPUT TAPE 6, 601, IA, IB, IC, AREA
601 FORMAT (4H A= ,I5,5H B= ,I5,5H C= ,I5,8H AREA= ,F10.2,
+ 13H SQUARE UNITS)
STOP
END
Слайд 9Программы – это операции на предопределенных типах данных
Локальная память
(самые быстрые
вычисления): register type ident = value; auto type ident =
value.Статическая память (сохранение данных в процедурах) static type ident = value; extern type ident.
Динамическая память (собственно работа с большими массивами информации) static или extern type *ident = new( size );
Элементарные типы данных:
целые числа:
bool - логические true | false
enum – именные перечисления
char – текстовые символы
short – индексы из 2 байт
int – число (слово) из 4 байт
long long – двойное слово
действительные числа:
float – число из 4 байт
double – число из 8 байт
составные числа – структуры:
struct , union, ++ class
Слайд 12D (Ди) язык программирования
A abstract alias align asm assert auto
B body bool break byte
C case cast catch char
class const continue D dchar debug default delegate deprecated do double
E else enum export extern
F false final finally float for foreach function
G goto
I ifIf immutable import in inout int interface invariant isIs
L long lazy
M macro mixin module
N new nothrow null
O out override
P package pragma private protected public pure
R real ref return
S scope short static struct super switch synchronized
T template this throw true try typeid typeof
U ubyte uint ulong union unittest ushort
V version void
W wchar while with почти Algol - 89 ключевых слов
Слайд 20OpenMP – параллельное исполнение команд в С
#include
// комментарии (макросы) тоже в деле
int main () // Ключевых
слов{ // теперь почти нет
int nthreads = 4; //
omp_set_num_threads(nthreads); // программистское
#pragma omp parallel // творчество
{ // почти безгранично
int id = omp_get_thread_num();
printf("Hello World from thread = %d", id);
printf(" with %d threads\n",omp_get_num_threads());
}
printf("all done, with hopefully %d threads\n",nthreads);
}
Слайд 21Язык D – Ver.2 / Tango (тень языка Ada)
// Программа
показывает на консоли аргументы командной строки // Функция main является точкой входа
программы, // а args — массив с параметрами запуска программы.module main; // Желательно объявлять
version (Tango) import tango.io.Stdout; else import std.stdio; // для writefln() из Phobos
void main( char[][] args )
{ foreach( int i, char[] a; args ) { version (Tango) Stdout.formatln("args[{}] = {}", i, a); else writefln("args[%d] = '%s'", i, a); } // D.1 – императивный и объектно-ориентированный
} // D.2 – функциональная и многопоточная парадигма
Слайд 22Вопросы:
Ключевые слова и зарезервированные идентификаторы языков программирования
(объявление данных и исполняемые
операторы);
Математические и логические операции исторических языков программирования
(математические и программные выражения)
Приоритеты
и последовательность исполняемых и константных выражений (литералы времени компиляции и интерпретация выражений на этапах сборки и исполнения программы).…
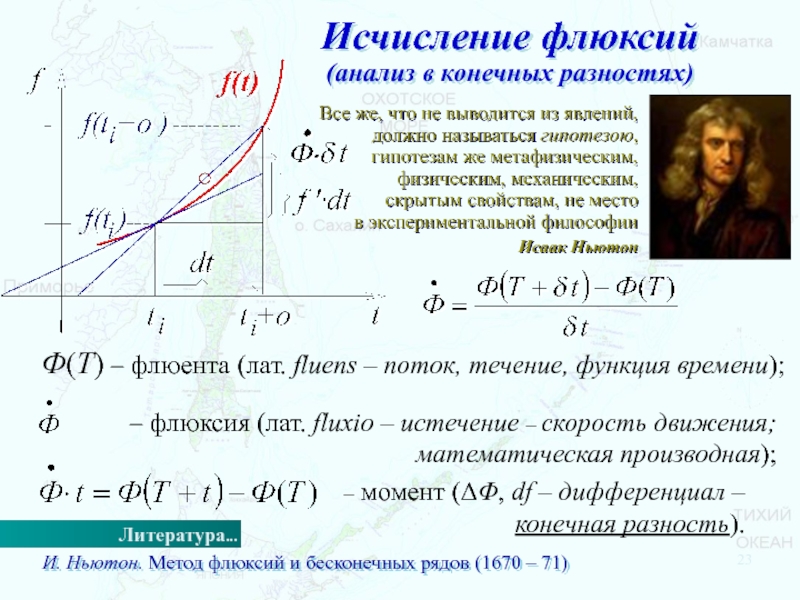
Слайд 23Исчисление флюксий
(анализ в конечных разностях)
Все же, что не выводится из
явлений, должно называться гипотезою, гипотезам же метафизическим, физическим, механическим, скрытым свойствам, не место в экспериментальной
философииИсаак Ньютон
.
Ф(T) – флюента (лат. fluens – поток, течение, функция времени);
– флюксия (лат. fluxio – истечение – скорость движения; математическая производная);
– момент (DF, df – дифференциал – конечная разность).
Литература...
И. Ньютон. Метод флюксий и бесконечных рядов (1670 – 71)
Слайд 24Исчисление флюксий
Дифференцирование – поиск флюксий по Ньютону – операция поэлементного
добавления моментов к каждому члену полиноминального выражения. Пусть, например: Ф(x,y,z,t) =
x2 + yz, добавляя моменты:Вычитая Ф(Т) и возвращая t в знаменатель:
Слайд 25Координатные системы отсчета
( абсолютные и локальные базисы )
Время:
1. Абсолютное, истинное
математическое время само по себе и по самой своей сущности,
без всякого отношения к чему-либо внешнему, протекает равномерно и иначе называется длительностью. Относительное, кажущееся или обыденное время есть или точная, или изменчивая, постигаемая чувствами, внешняя, совершаемая при посредстве какого-либо движения мера продолжительности, употребляемая в обыденной жизни вместо истинного, или математического, времени, как то: час, день, месяц, год.Слайд 26Координатные системы отсчета
( абсолютные и локальные базисы )
Пространство:
2. Абсолютное пространство,
по самой своей сущности, безотносительно к чему бы то ни
было внешнему, остается всегда одинаковым и неподвижным. Относительное - есть его мера или какая-либо огра-ниченная подвижная часть, которая определяется нашими чувствами по положению его относительно некоторых тел и которое в обыденной жизни принимается за пространство неподвижное. …Возможно, что не существует такого равномерного движе-ния, которым время могло измеряться с совершенной точно-стью. Все движения могут ускоряться или замедляться, течение же абсолютного времени[1] изменяться не может. … [1] Мировая скалярная величина.
Слайд 27Вычислительные объекты
1) Скаляр – числовая величина, не зависящая от системы
отсчета, являющаяся либо инвариантом пространственно-временных преобразований, либо физической (эмпирической) константой.
Используется в операциях произведения с любыми объектами;2) Вектор – сложный числовой объект, задает пространственно ориентированное внешнее воздействие или реакцию. Векторы всегда связаны с собственным пространственным базисом (СК). Участвует в операциях сложения с определенными векторами из той же СК. Произведение допускается только с векторами из дуального (связанного) базиса, или с тензорами с дуальными компонентами – для замены или уточнения опорного базиса;
3) Тензор II ранга – образует линейный пространственный базис, фиксирующий локальную систему отсчета; кинематические и конвективные свойства; или внутреннюю энергию (живые силы) моделируемых процессов в механике и физике. Участвуют в произведениях с векторами и тензорами для преобразования СК, а также в анализе свойств моделируемых физических явлений.
Слайд 28Координатные системы отсчета
( абсолютные и локальные базисы )
Для перевода скалярной
величины из локальной системы отсчета – R' в абсолютную –
Х, необходимо сложить локальную длину отрезка – а, с величиной начального отсчета смещенной (относительной) метки R’:А = R’ + a.
Все слагаемые величины должны иметь одинаковые физические размерности. Операция умножения (кратности) возможна только в случае использования безразмерного множителя параметра, который влияет на изменение длины (деформацию) этого локального вектора – а.
Слайд 29Координатные системы отсчета
( абсолютные и локальные базисы )
В качестве абсолютной
системы отсчета выбирается симплекс координатных осей, соответствующий размерности используемого пространства,
при этом все базисные оси должны быть взаимно перпендикулярны (ортогональны), иметь одинаковые физические размерности и равные единичные меры (ортонормированы). Удовлетворяющие таким требованиям системы координат называют ортогональными и ортонормированными или – декартовыми.Местная система координат образуется локальным базисом на некомпланарных векторах единичной длины:
r = ri = rij = { x, y, z }
Слайд 30Координатные системы отсчета
( компьютерное представление )
typedef struct { char s;
int d } integer; // для индексов, typedef struct { char
s; double d } real; // для чисел,typedef struct { char s; double X,Y,Z } Point; // координатная точка в общей системе отсчета typedef struct { char s; double x,y,z } point; // координатный отсчет внутри локального базиса
Уровень языка С
(как макроассемблера)
Слайд 31Исчисление векторов
(определения тензорной математики)
Литература...
Н.Е. Кочин. Векторное исчисление и
начала тензорного исчисления, 1965 (9-е издание)
Н.А. Кильчевский. Элементы тензорного
исчисления и его приложения к механике. 1954Векторы, как вычислительные объекты характеризуются:
1 – масштабным множителем (подобно скаляру);
2 – ориентацией – смещением в координатных осях;
3 – принадлежностью к одному конкретному базису !!!
R – абсолютные координаты место-положения локального базиса
а – локальный вектор в собственной (связанной) системе отсчета r
Ковариантные и
контравариантные
компоненты
вектора.
Слайд 32Исчисление векторов
(определения – вполне реальная альтернатива)
Литература...
Н.Е. Кочин. Векторное
исчисление и начала тензорного исчисления, 1965 (9-е издание)
Н.А. Кильчевский.
Элементы тензорного исчисления и его приложения к механике. 1954Векторы, как вычислительные объекты характеризуются:
1 – масштабным множителем (подобно скаляру);
2 – ориентацией – смещением в координатных осях;
3 – принадлежностью к одному конкретному базису
R – абсолютные координаты место-положения локального базиса
а – локальный вектор в собственной (связанной) системе отсчета r
Ковариантные и
контравариантные
компоненты вектора
== компьютерные индексы.
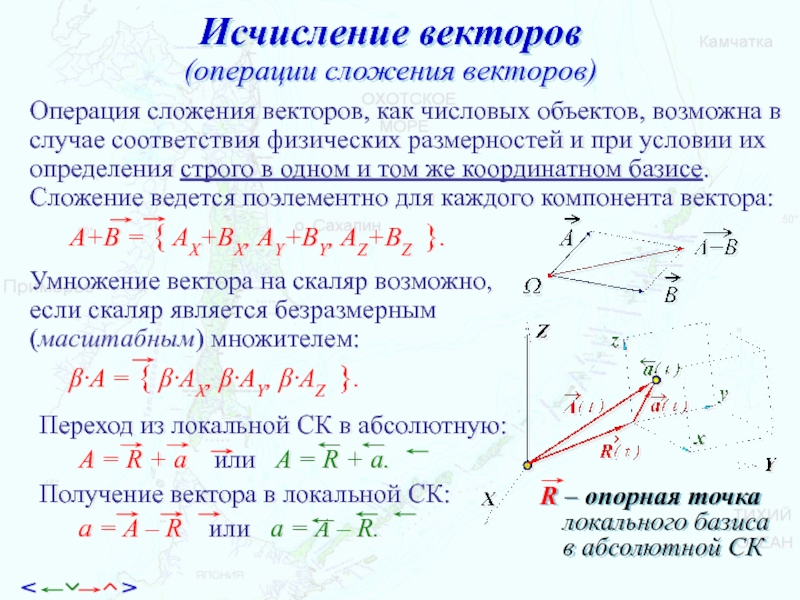
Слайд 33Исчисление векторов
(операции сложения векторов)
Операция сложения векторов, как числовых объектов, возможна
в случае соответствия физических размерностей и при условии их определения
строго в одном и том же координатном базисе. Сложение ведется поэлементно для каждого компонента вектора:A+B = { AX+BX, AY+BY, AZ+BZ }.
Умножение вектора на скаляр возможно,
если скаляр является безразмерным
(масштабным) множителем:
b·A = { b·AX, b·AY, b·AZ }.
Переход из локальной СК в абсолютную:
A = R + a или A = R + a.
Получение вектора в локальной СК:
a = A – R или a = A – R.
R – опорная точка локального базиса
в абсолютной СК
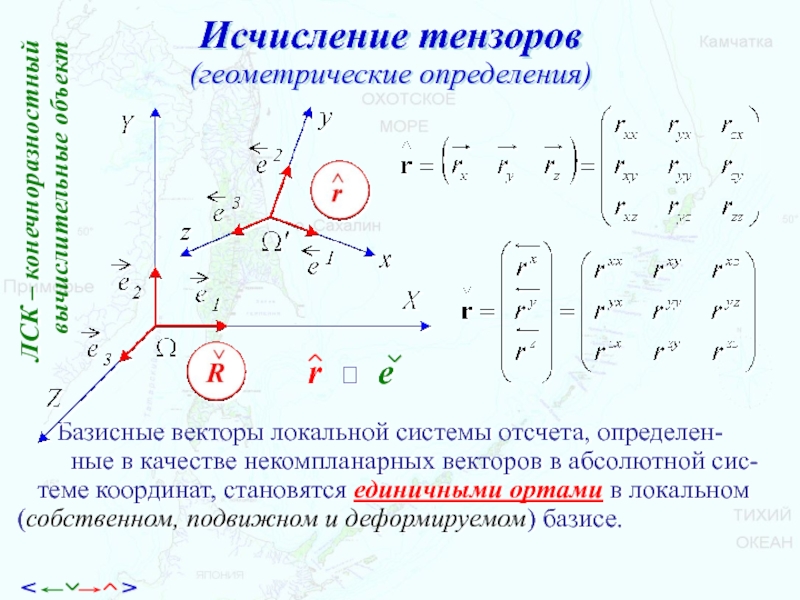
Слайд 34Исчисление тензоров
(геометрические определения)
Базисные векторы локальной системы отсчета, определен-
ные в качестве некомпланарных векторов в абсолютной сис-
теме координат, становятся единичными ортами в локальном (собственном, подвижном и деформируемом) базисе.ЛСК – конечноразностный
вычислительные объект
Слайд 35Исчисление тензоров
(геометрические преобразования)
В пространственном исчислении (в трех-мерном поле) в качестве
разделенных
разностей Ньютона:
появляется базисный тензор, образованный
координатным трехгранником конечно-
разностных пространственных отсчетов.Ax = Rx +rxx·ax+rxy·ay+rxz·az ;
Ay = Ry +ryx·ax+ryy·ay+ryz·az ;
Az = Rz +rzx·ax+rzy·ay+rzz·az .
Тензорные операции – матричные?
Вектор Тензор Вектор
Слайд 36Объем базиса
– детерминант
Исчисление тензоров
(интерпретация геометрических базисов – линейная алгебра)
В дуальном базисе оси координат образуют
нормали к исходному трехгранникуСхема Саррюса
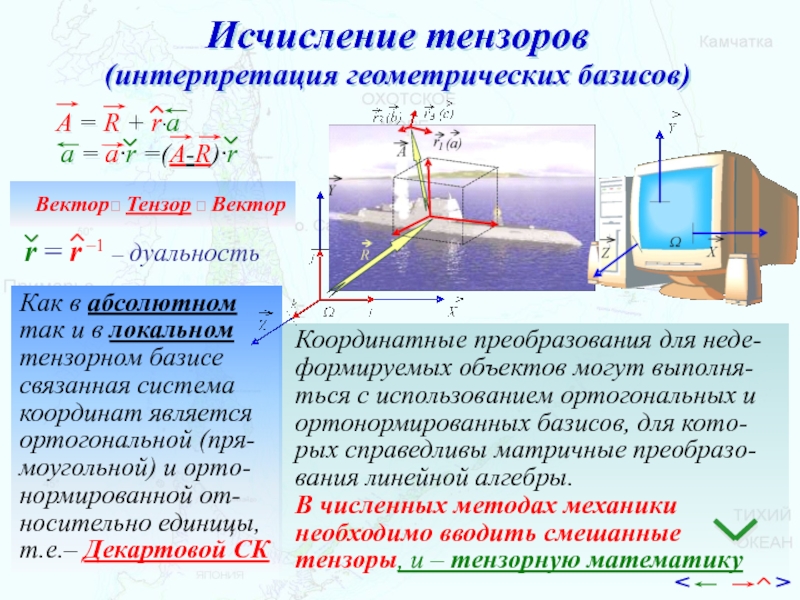
Слайд 37Исчисление тензоров
(интерпретация геометрических базисов)
Координатные преобразования для неде-формируемых объектов могут выполня-ться
с использованием ортогональных и ортонормированных базисов, для кото-рых справедливы матричные
преобразо-вания линейной алгебры.В численных методах механики необходимо вводить смешанные тензоры, и – тензорную математику
Вектор Тензор Вектор
Как в абсолютном
так и в локальном
тензорном базисе
связанная система
координат является
ортогональной (пря-
моугольной) и орто-
нормированной от-
носительно единицы,
т.е.– Декартовой СК
Слайд 38Исчисление тензоров
(продолжение и замечания)
В исчислении флюксий Ньютона:
Выражение для скорости в
следующий момент времени
В приращение координат
войдет тензор вращения и деформации
собственного базиса:– тензор конвективных скоростей (живых сил) в ЛСК.
1. Запрет повышения ранга тензора в произведении (т.к.результ.вырожден)
2. Ограничение на использование скалярных умножений (только оценки)
3. Жесткий контроль принадлежности к связанному базису
во всех вычислительных объектах и расчетных операциях.
Слайд 39Занятие третье, 21 сентября
3++ Практические занятия …
Рассмотрение структуры пакета для
масштабирования и графических построений плоскости.
Особенности проведения математического анализа и
вычислительных экспериментов.Графические пакеты, настройка и выполнение стандартных примеров программ с использование OpenGL
…
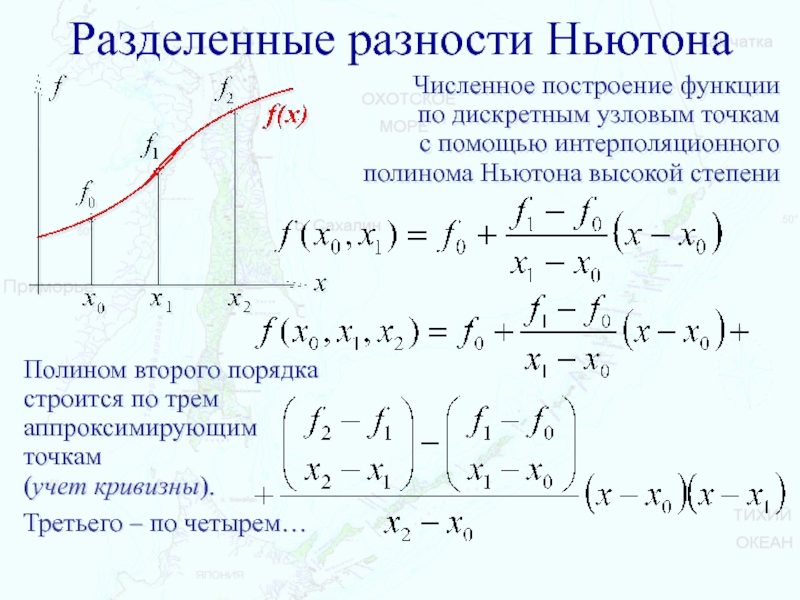
Слайд 41Разделенные разности Ньютона
Численное построение функции
по дискретным узловым точкам
с помощью интерполяционного
полинома Ньютона высокой степени
Полином второго порядка строится по трем
аппроксимирующим точкам
(учет кривизны).Третьего – по четырем…
Слайд 43Интерполирующие многочлены
Форма Ньютона:
Форма Лагранжа:
схема спуска минимизирует количество вычислительных операций
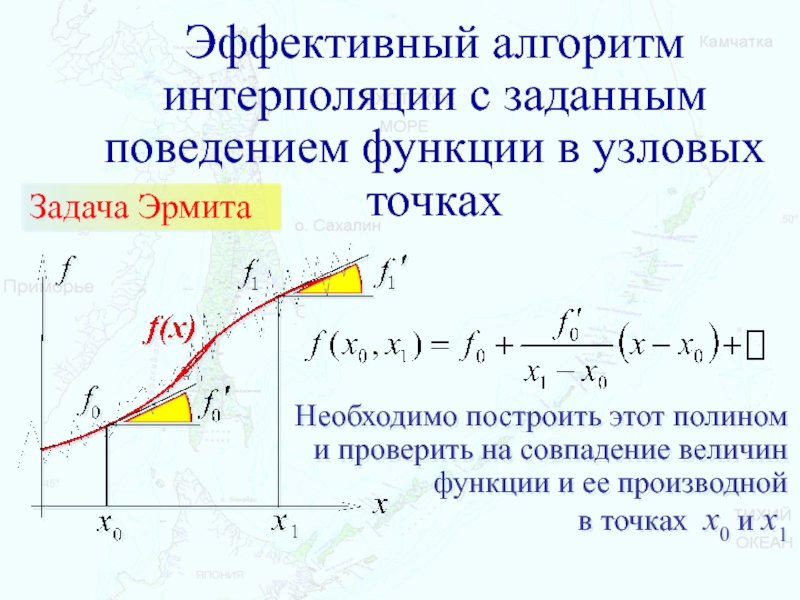
Слайд 44Эффективный алгоритм интерполяции с заданным поведением функции в узловых точках
Необходимо
построить этот полином и проверить на совпадение величин функции и
ее производной в точках x0 и x1Задача Эрмита
Слайд 45Практика, 14 сентября, 2-3 пара
Персональные компьютеры
www.equation.com – Fortran, C++
dlang.org
– D-compiler (GDC или DigitalMars)
www.codeblocks.org –
среда разработкиwxdsgn.sourceforge.net – xWindow, Dev-C++
Классный компьютер
login: student101e
password: student101e \\ws101-operator\Shared folder









































![Звуки [х], [ х′ ].
Позначення їх
буквами Х, х ( ха](/img/thumbs/35dbf8338bb9957e36032e16906181a0-800x.jpg)
















