Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы теории стохастических систем
Содержание
- 1. Основы теории стохастических систем
- 2. Содержание лекцийОбщие сведения о стохастических системахСлучайные события
- 3. Общие сведения о стохастических системах (1) В
- 4. Общие сведения о стохастических системах (2)Основной характеристикой
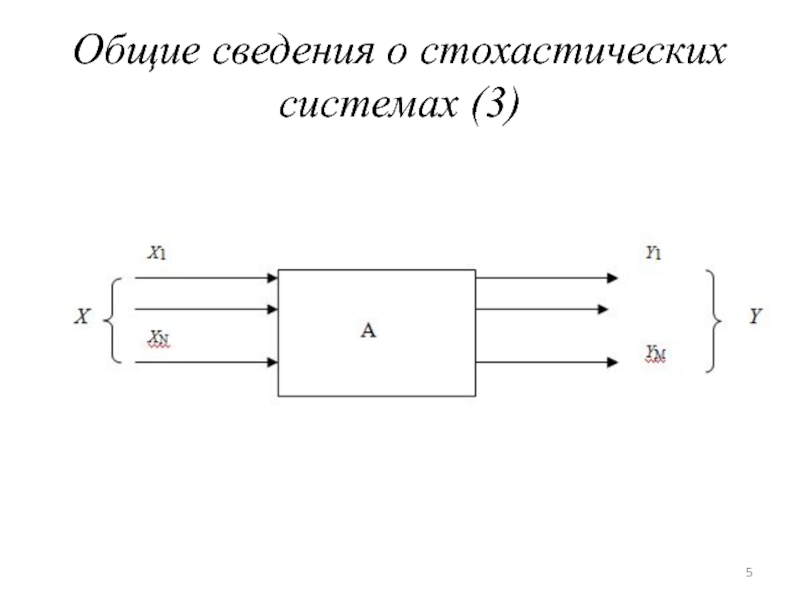
- 5. Общие сведения о стохастических системах (3)
- 6. Общие сведения о стохастических системах (4)Стохастической системой
- 7. Общие сведения о стохастических системах (5)Математической моделью
- 8. Общие сведения о стохастических системах (6) Классификация
- 9. Общие сведения о стохастических системах (7)Теория вероятностей
- 10. Случайные события (1)Будем называть испытанием (опытом, наблюдением,
- 11. Случайные события (2)
- 12. Случайные события (3)Если вероятность появления события В
- 13. Случайные события (4)Пример1. В ящике лежат шары:
- 14. Случайные события (5)Пример2. В вопросах к
- 15. Случайные величины(1)Под случайной величиной понимается величина, которая
- 16. Случайные величины(2)Закон распределения дискретной случайной величины представляет собой
- 17. Случайные величины(3)Математическое ожидание дискретной случайной величины есть сумма
- 18. Случайные величины(4)Дисперсия дискретной случайной величины есть математическое ожидание
- 19. Случайные величины(5)Среднее квадратическое отклонение дискретной случайной величины, оно
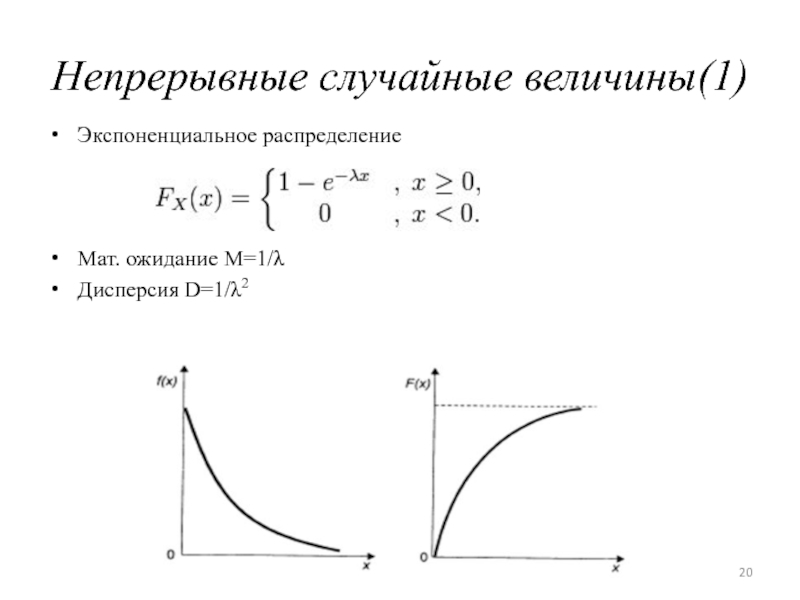
- 20. Непрерывные случайные величины(1)Экспоненциальное распределениеМат. ожидание M=1/λДисперсия D=1/λ2
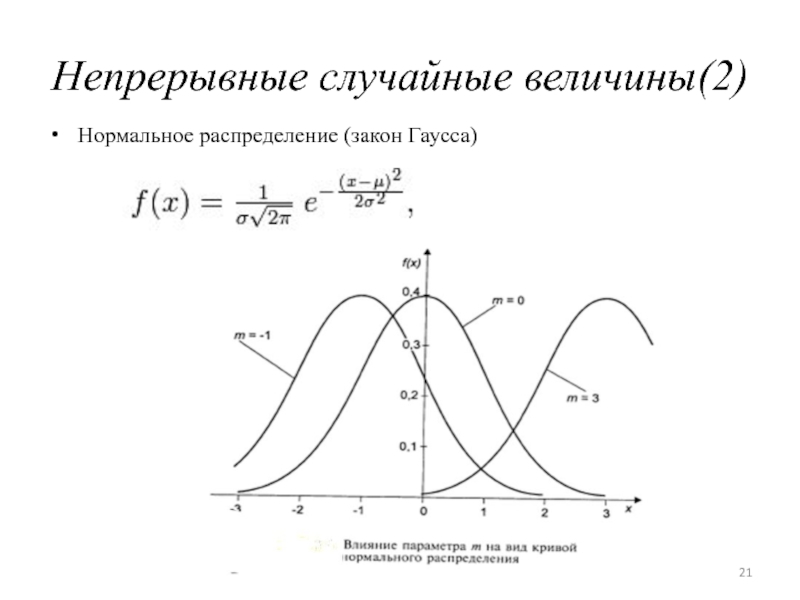
- 21. Непрерывные случайные величины(2)Нормальное распределение (закон Гаусса)
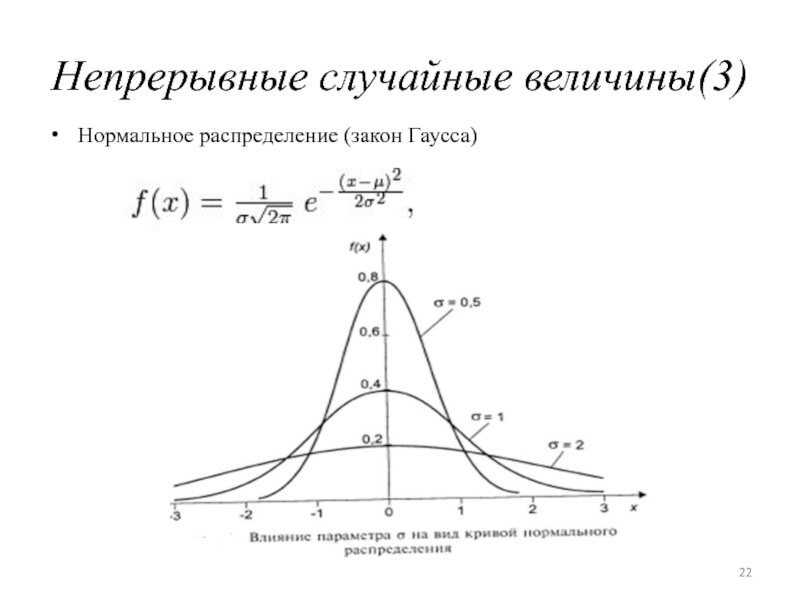
- 22. Непрерывные случайные величины(3)Нормальное распределение (закон Гаусса)
- 23. Непрерывные случайные величины(4)С помощью нормального распределения определяются
- 24. Непрерывные случайные величины(5)Распределение t Стьюдента – это распределение случайной
- 25. Непрерывные случайные величины(6)Распределение Фишера – это распределение
- 26. Многомерное распределение дискретных и непрерывных случайных величин
- 27. Многомерное распределение дискретных и непрерывных случайных величин
- 28. Многомерное распределение дискретных и непрерывных случайных величин
- 29. Многомерное распределение дискретных и непрерывных случайных величин
- 30. Многомерное распределение дискретных и непрерывных случайных величин
- 31. Корреляционный анализКорреляционный анализ - метод, позволяющий обнаружить зависимость
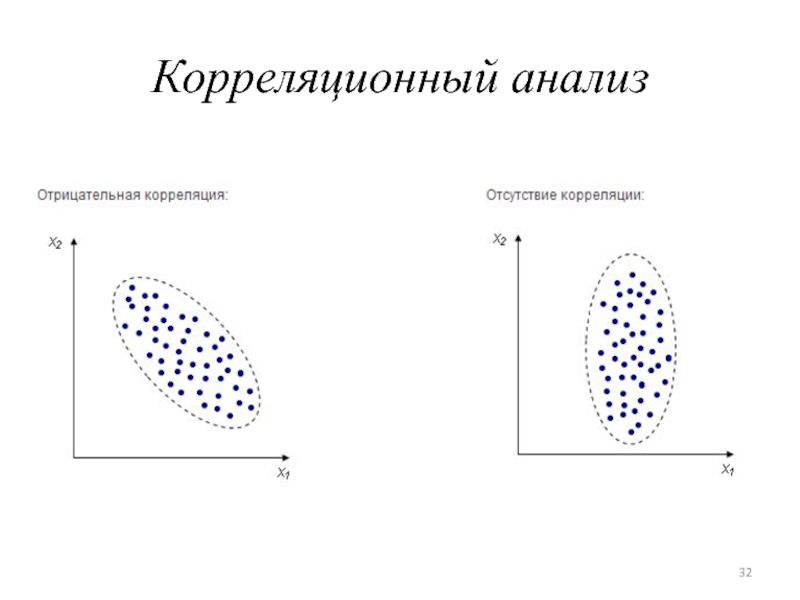
- 32. Корреляционный анализ
- 33. Корреляционный анализДля численной характеристики параметров анализа вводится
- 34. Скачать презентанцию
Содержание лекцийОбщие сведения о стохастических системахСлучайные события Случайные величины Непрерывные случайные величиныМногомерное распределение дискретных и непрерывных случайных величин Корреляционный анализ
Слайды и текст этой презентации
Слайд 2Содержание лекций
Общие сведения о стохастических системах
Случайные события
Случайные величины
Непрерывные
случайные величины
Слайд 3Общие сведения о стохастических системах (1)
В практических задачах системой обычно
называют любую совокупность взаимодействующих предметов любой природы. Примерами систем являются
окружающий нас мир или какая-либо часть, завод, вычислительная машина, летательный аппарат и т.д.Величины, определяющие внешнее воздействие на систему, называются входными сигналами. Величины, определяющие действие системы на окружающую среду, на другие системы, называются выходными сигналами.
Кроме входных и выходных сигналов для построения математической модели системы приходится вводить некоторые вспомогательные величины, характеризующие действия различных частей системы друг на друга (внутренние взаимодействия частей системы). Все эти величины, характеризующие состояние системы в каждый данный момент времени, называются переменными состояния системы.
Слайд 4Общие сведения о стохастических системах (2)
Основной характеристикой системы является ее
оператор, определяющий механизм формирования выходного сигнала по данному входному сигналу.
Оператор детерминированной системы ставит в соответствие каждому входному сигналу один определенный выходной сигнал – т.о. отображает пространство входных сигналов X в пространство выходных сигналов Y.у(t) = Ax(t)
Детерминированная система называется физически возможной, если значение ее выходного сигнала у(t) в каждый момент времени t не зависит от значений вход
Действие системы состоит в том, что данному элементу x пространства входных сигналов Х она ставит в соответствие некоторый элемент у пространства выходных сигналов Y ного сигнала x(τ) при τ>t.
Слайд 6Общие сведения о стохастических системах (4)
Стохастической системой называется такая система,
которая ставит в соответствие любому входному сигналу x€X определенное распределение
вероятностей в пространстве выходных сигналов Y. Поведение стохастической системы описывается переходной вероятностьюμy = μ(Ey|x)
принадлежности выходного сигнала множеству Ey€Y при данном входном сигнале x€X. Функция μy называется условно вероятностной мерой или решающей функцией системы.
Стохастическая система называется физически возможной, если распределение значения ее выходного сигнала Y(t) в любой момент t не зависит от значений входного сигнала x(τ) при τ>t.
Слайд 7Общие сведения о стохастических системах (5)
Математической моделью системы называется совокупность
четырех элементов:
1) пространства состояний,
2) пространства входных сигналов,
3) пространства
выходных сигналов,4) соотношений, связывающих входной и выходной сигналы и вектор состояния системы.
Слайд 8Общие сведения о стохастических системах (6)
Классификация систем по типу
поведения
Общее абстрактное описание (абстрактная модель) лишь отражает характер описания и
общие свойства систем широкого класса с различным типом поведения. Для построения модели удобнее использовать некоторые типовые математические схемы, отражающие те или иные типы поведения реальных моделируемых систем.По числу состояний модели делятся на статические и динамические. Для статических моделей характерным является то, что выход системы (или ее характеристики) в некоторый момент времени определяется значением входного сигнала в тот же момент времени: .
В плане абстрактного описания эти системы можно определить как системы с одним значением состояния, то есть предыстория не изменяет состояния и, стало быть, не влияет на выход. Если возможных состояний множество, то систему (и модель) классифицируют как динамическую.
Слайд 9Общие сведения о стохастических системах (7)
Теория вероятностей изучает количественные закономерности,
которым следуют случайные явления, если эти явления определяются событиями известной
вероятности. Соответственно, математическая статистика является связующим звеном между теорией вероятностей и явлениями реального мира, поскольку позволяет сформулировать оценки вероятности тех или иных событий на основе анализа статистических данных.Математическая статистика — это наука, изучающая методы вскрытия закономерностей, свойственных большим совокупностям однородных объектов или событий, на основании их выборочного обследования (либо большим массивам данных, полученных в результате наблюдения за одним и тем же объектом на протяжении достаточно протяженного интервала времени).
Слайд 10Случайные события (1)
Будем называть испытанием (опытом, наблюдением, измерением) некоторую совокупность
действий. Предполагается, в общем случае, что испытание можно повторить неограниченное
число раз.Событием (случайным событием) называется всякий факт, который может произойти или не произойти в результате опыта. События обозначаются буквами А, B, C, D, …
Вероятностью события называется численная мера возможности появления события в результате данного опыта. Вероятность события А обозначается Р(А). Событие W, которое обязательно произойдет в результате опыта, называется достоверным: Р(W) = 1. Событие Æ, которое никогда не может произойти в результате опыта, называется невозможным: Р(Æ) = 0. Событие А, о котором нельзя заранее сказать произойдет оно или нет в результате опыта, называется случайным: 0<Р(А)<1.
Слайд 12Случайные события (3)
Если вероятность появления события В изменяется в зависимости
от того, произошло или нет событие А, то такие события
называются зависимыми. Вероятность события В при условии, что событие А уже произошло, обозначается PA(B). Вероятность произведения зависимых событий определяется формулой P(AB)=P(A)× PA(B).Если события А и В несовместные, то Р(АВ)=0.
Формула для вычисления вероятности суммы двух событий, все равно каких, совместных или нет, имеет вид: Р(А+В)=Р(А)+Р(В)-Р(АВ).
Полной группой событий называется несколько событий таких, что в результате опыта непременно должно произойти хотя бы одно из них.
Классическое определение вероятности. Пусть в результате опыта может произойти одно из n элементарных событий, причем событию А благоприятствуют m из них m. Тогда вероятностью события А называется отношение числа элементарных исходов, благоприятствующих появлению события А, к общему числу равновозможных элементарных исходов: Р(А)= m/n.
Слайд 13Случайные события (4)
Пример1. В ящике лежат шары: 4 белых, 10
красных, 8 зеленых, 9 коричневых. Из ящика вынимают один шар.
Пользуясь теоремой сложения вероятностей определить, какова вероятность, что шар окажется цветным (не белым) ?Решение.
Всего в ящике лежит N=4+10+8+9=31 шар.
Вероятность вытащить красный шар
Вероятность вытащить зеленый шар
Вероятность вытащить коричневый шар
Т.к. эти три события несовместны, то пользуясь теоремой сложения вероятностей определим вероятность того, что шар окажется цветным (не белым)
Слайд 14Случайные события (5)
Пример2. В вопросах к зачету имеются 75%
вопросов, на которые студенты знают ответы. Преподаватель выбирает из них
два вопроса и задает их студенту. Определить вероятность того, что среди полученных студентом вопросов есть хотя бы один, на который он знает ответ.Решение.
Вероятность вытащить знакомый вопрос p=0.75,
незнакомый q=1-p=1-0.75=0.25
Пусть H1 - гипотеза, что студент не знает ни одного из 2-х вопросов. Вероятность этой гипотезы:
Искомая вероятность соответственно равна:
Слайд 15Случайные величины(1)
Под случайной величиной понимается величина, которая в результате опыта
со случайным исходом принимает то или иное значение. Возможные значения
случайной величины образуют некоторое множество, которое называется множеством возможных значений случайной величины. Обозначения случайной величины: X, Y, Z; возможные значения случайной величины: x, y, z.Дискретной называют случайную величину, значения которой изменяются не плавно, а скачками, т.е. могут принимать только некоторые заранее определённые значения. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счётным множеством) Для сравнения - непрерывная случайная величина может принимать любые значения из некоторого числового промежутка: например, температура воздуха в определённый день, вес ребёнка в каком-либо возрасте, и т.д.
Слайд 16Случайные величины(2)
Закон распределения дискретной случайной величины представляет собой перечень всех её
возможных значений и соответствующих вероятностей. Сумма всех вероятностей Σpi = 1.
Закон распределения также может быть задан аналитически (формулой) и графически (многоугольником распределения, соединяющим точки (xi; pi)Функция распределения случайной величины - это вероятность того, что случайная величина (назовём её ξ) примет значение меньшее, чем конкретное числовое значение x:
F(X) = P(ξ < X).
Для дискретной случайной величины функция распределения вычисляется для каждого значения как сумма вероятностей, соответствующих всем предшествующим значениям случайной величины. Ниже будет приведён пример, разъясняющий смысл сказанного
Слайд 17Случайные величины(3)
Математическое ожидание дискретной случайной величины есть сумма произведений всех её
возможных значений на их вероятности: M(X) = x1p1 + x2p2 + ... +
xnpnСвойства математического ожидания. 1) Математическое ожидание постоянной величины равно самой величине: М(С) = С 2) Постоянный множитель можно выносить за знак математического ожидания: М(СХ) = С·М(Х) 3) Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых: М(Х1 + Х2 + …+ Хn) = М(Х1) + М(Х2) + ... + М(Хn) 4) Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей: М(Х1 · Х2 · ... · Хn) = М(Х1) · М(Х2) · ... · М(Хn)
Слайд 18Случайные величины(4)
Дисперсия дискретной случайной величины есть математическое ожидание квадрата отклонения случайной
величины от её математического ожидания:
D(X) = (x1 - M(X))2p1 + (x2 - M(X))2p2 +
... + (xn- M(X))2pn = x21p1 + x22p2 + ... + x2npn - [M(X)]2Свойства дисперсии.
1) Дисперсия постоянной величины равна нулю: D(С) = 0 2) Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СХ) = С2 · D(Х) 3) Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых: D(Х1 ± Х2 ± ... ± Хn) = D(Х1) + D(Х2) + ... + D(Хn)
Слайд 19Случайные величины(5)
Среднее квадратическое отклонение дискретной случайной величины, оно же стандартное отклонение
или среднее квадратичное отклонение есть корень квадратный из дисперсии: σ(X) =
√D(X)Мода дискретной случайной величины Mo(X) - это значение случайной величины, имеющее наибольшую вероятность. На многоугольнике распределения мода - это абсцисса самой высокой точки. Бывает, что распределение имеет не одну моду.
Асимметрия (коэффициент асимметрии) случайной величины (и дискретной, и непрерывной) As(X) - величина, характеризующая степень асимметрии распределения относительно математического ожидания.
Эксцесс (коэффициент эксцесса) случайной величины (и дискретной, и непрерывной) Ex(X) - величина, характеризующая степень островершинности или плосковершинности распределения, т.е. степень так называемого «выпада».
Слайд 20Непрерывные случайные величины(1)
Экспоненциальное распределение
Мат. ожидание M=1/λ
Дисперсия D=1/λ2
Слайд 23Непрерывные случайные величины(4)
С помощью нормального распределения определяются три распределения, которые
в настоящее время часто используются при статистической обработке данных. В
дальнейших разделах книги много раз встречаются эти распределения.Распределение Пирсона (хи - квадрат) – распределение случайной величины
где случайные величины X1, X2,…, Xn независимы и имеют одно и тоже распределение N(0,1). При этом число слагаемых, т.е. n, называется «числом степеней свободы» распределения хи – квадрат.
Слайд 24Непрерывные случайные величины(5)
Распределение t Стьюдента – это распределение случайной величины
где случайные величины U и X независимы, U имеет
распределение стандартное нормальное распределение N(0,1), а X – распределение хи – квадрат с n степенями
свободы. При этом n называется «числом степеней свободы» распределения Стьюдента.Распределение применяют при оценивании математического ожидания, прогнозного значения и других характеристик с помощью доверительных интервалов, по проверке гипотез о значениях математических ожиданий, коэффициентов регрессионной зависимости, гипотез однородности выборок и т.д.
Слайд 25Непрерывные случайные величины(6)
Распределение Фишера – это распределение случайной величины
где случайные
величины Х1 и Х2 независимы и имеют распределения хи – квадрат с числом степеней
свободы k1 и k2 соответственно. При этом пара (k1, k2) – пара «чисел степеней свободы» распределения Фишера, а именно, k1 – число степеней свободы числителя, а k2 – число степеней свободы знаменателя.Распределение Фишера используют при проверке гипотез об адекватности модели в регрессионном анализе, о равенстве дисперсий и в других задачах прикладной статистики
Слайд 26Многомерное распределение дискретных и непрерывных случайных величин
Многомерной случайной величиной называется
величина, которая при проведении опыта принимает в качестве своего значения
не число, а целый набор чисел, заранее не известно каких. Эти наборы, которые случайная величина может принять, образуют множество ее возможных значений. Таким образом, хотя конкретный набор не предугадаешь, он будет из множества возможных наборов (часто это множество хорошо известно).Аналогично одномерным случайным величинам различают дискретные многомерные случайные величины (их составляющие дискретны) и непрерывные многомерные случайные величины, которые устроены более сложно (их составляющие непрерывны).
Слайд 27Многомерное распределение дискретных и непрерывных случайных величин
Многомерные случайные величины
могут быть непрерывными, т.е. принимать любые значения в некоторой области к-мерного
пространства (например, упомянутые выше компоненты скорости молекулы). У них F( x1, x2, ... xk ) непрерывная функция всех аргументов. Для них определена к-мерная плотность распределения p( x1, x2, ... xk ), которая есть производная от функции распределения.Слайд 28Многомерное распределение дискретных и непрерывных случайных величин
Многомерные случайные величины
могут быть дискретными, т.е. каждая компонента случайного вектора может принимать только
конечное или счетное множество определенных значений. Например, рассмотрим эксперимент по бросанию одновременно двух костей, с каждым элементарным событием свяжем два числа ( z1, z2 ), где z1 - число очков на первой кости, z2 - сумма очков на двух костях. Тогда ( z1, z2 ) - двумерная случайная величина, поскольку известна вероятность р( хi, хk ) пересечения событий, состоящих в том, что z1 примет значение хi, а z2 - хk .Слайд 29Многомерное распределение дискретных и непрерывных случайных величин
Математическим ожиданием многомерной случайной
величины называется вектор, компоненты которого являются математическим ожиданием каждой отдельной
компоненты случайного вектора. M( z1, z2, ... zk ) = ( Mz1, Mz2, ... Mzk ).Дисперсия многомерной случайной величины описывается ковариационной матрицей .
Это таблица чисел размерности К×К для К-мерной величины, у которой на диагонали стоят дисперсии соответствующих одномерных величин, вычисляемых обычным образом, а ij-тым элементом является bij - коэффициент ковариации i-той и j-той компоненты случайного вектора.
Слайд 30Многомерное распределение дискретных и непрерывных случайных величин
Коэффициент ковариации случайных величин
zi , zj , обозначаемый иногда как cov(zi,zji), есть математическое ожидание произведения
отклонений каждой из этих величин от своего математического ожидания:Слайд 31Корреляционный анализ
Корреляционный анализ - метод, позволяющий обнаружить зависимость между несколькими случайными
величинами.
с помощью корреляционного анализа решаются следующие задачи:
- отбор факторов,
оказывающих наиболее существенное влияние на результативную переменную, на основании измерения степени связи между ними; - - обнаружение ранее неизвестных причинных связей
Например, измеряем рост и вес человека, каждое измерение представлено точкой в двумерном пространстве (положительная корреляция):
Слайд 33Корреляционный анализ
Для численной характеристики параметров анализа вводится понятие коэффициент корреляции.
Он рассчитывается следующим образом:
Есть массив из n точек {x1,i, x2,i}
Рассчитываются средние значения для
каждого параметра: И коэффициент корреляции:
r изменяется в пределах от -1 до 1. В данном случае это линейный коэффициент корреляции, он показывает линейную взаимосвязь между x1 и x2: r равен 1 (или -1), если связь линейна.
Коэффициент r является случайной величиной, поскольку вычисляется из случайных величин