Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Особенности подготовки учащихся к итоговой аттестации в форме ОГЭ. Приёмы
Содержание
- 1. Особенности подготовки учащихся к итоговой аттестации в форме ОГЭ. Приёмы
- 2. Трудности решения геометрических задачНеалгоритмичность задачНеобходимость выбора метода
- 3. Необходимые условия успеха при решении задач по
- 4. Причины ошибок в решении геометрических задачНезнание и/или
- 5. Специфические особенности методов решения геометрических задачБольшое разнообразиеВзаимозаменяемостьТрудность
- 6. Некоторые методы решения геометрических задач второй части ОГЭПрименение ключевых задачМетод вспомогательных построенийПереход к равновеликим фигурамМетод площадей
- 7. Метод решения: Удвоение медианы Медиана прямоугольного
- 8. Следствие из свойства медианы к гипотенузе. Ключевая
- 9. Использование введения буквенных обозначений величин. Ключевая задача
- 10. Метод вспомогательных построений При решении некоторых
- 11. Применение свойства медианы к гипотенузе Найдите
- 12. Найдите гипотенузу прямоугольного треугольника с
- 13. Найдите острые углы прямоугольного треугольника,
- 14. Свойства площади треугольника Площади треугольников, имеющих общую
- 15. Метод вспомогательных построений. Использование осевой симметрии
- 16. Построение вспомогательных отрезков
- 17. В трапеции ABCD с основаниями
- 18. В трапеции ABCD с основаниями
- 19. В трапеции ABCD с основаниями
- 20. В параллелограмме ABCD площадь треугольника
- 21. Площадь трапеции АВСD равна площади
- 22. Дополнительные построения в трапеции.
- 23. Диагонали трапеции равны 3 и 5,
- 24. Дополнительные построения в трапеции. Метод удвоения
- 25. Метод площадей Идея метода: площади
- 26. Медиана BM треугольника ABC равна его
- 27. Свойство деления сторон треугольникаокружностью, вписанной в него. АМ = АЕBN = BЕCN = CM
- 28. В треугольник вписана окружность радиуса 4.
- 29. Метод решения: Введение вспомогательной окружности
- 30. Введение вспомогательной окружности В выпуклом четырехугольнике ABCD
- 31. Введение вспомогательной окружности∠ СAD = ∠ DСA
- 32. Введение вспомогательной окружности В трапеции ABCD
- 33. Рекомендации учащимся при решении геометрических задач
- 34. О чертежеХороший чертеж – помощникВсе, что «увидено», должно быть обоснованоСоблюдай пропорции и соотношенияИспользуй выносные чертежи
- 35. О поиске решения задачиТреугольник равнобедренный, следовательно …Две
- 36. Научить решать учащихся геометрические задачи
- 37. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Особенности подготовки учащихся к итоговой аттестации в форме ОГЭ. Приёмы
решения геометрических задач
Слайд 2Трудности решения геометрических задач
Неалгоритмичность задач
Необходимость выбора метода решения задачи и
теоремы для решения конкретной задачи (нескольких теорем) из большого набора
известных фактовНужно решить довольно много задач, чтобы научиться их решать.
Слайд 3Необходимые условия успеха при решении задач по геометрии
Уверенное владение основными
понятиями и их свойствами (определения, аксиомы, теоремы, базовые задачи)
Знание основных
методов и приёмов решения задачУмение комбинировать методы и приёмы решения задач
Наличие опыта решения задач
Слайд 4Причины ошибок в решении геометрических задач
Незнание и/или непонимание аксиом, определений,
теорем
Неумение их применять
Невнимательное чтение условия и вопроса задания
Вычислительные ошибки
Нарушения логики
в рассужденияхПринятие ошибочных гипотез
Недостатки в работе с рисунком
Слайд 5Специфические особенности методов решения геометрических задач
Большое разнообразие
Взаимозаменяемость
Трудность формального описания
Отсутствие чётких
границ применения (в отличие от алгебры)
Использованию комбинаций методов и приёмов.
Слайд 6Некоторые методы решения геометрических задач второй части ОГЭ
Применение ключевых задач
Метод
вспомогательных построений
Переход к равновеликим фигурам
Метод площадей
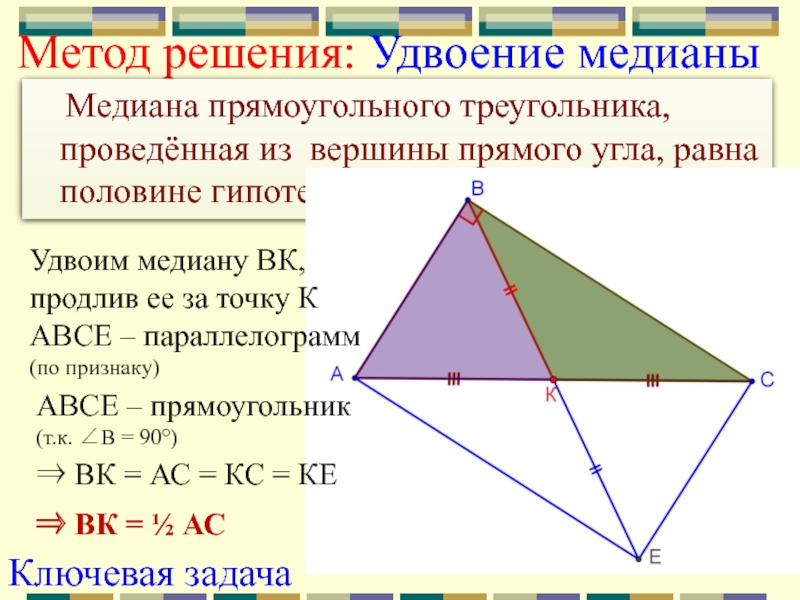
Слайд 7Метод решения: Удвоение медианы
Медиана прямоугольного треугольника, проведённая из
вершины прямого угла, равна половине гипотенузы.
АВСЕ – параллелограмм
(по признаку)
АВСЕ
– прямоугольник(т.к. В = 90°)
ВК = АС = КС = КЕ
ВК = ½ АС
Ключевая задача
Удвоим медиану ВК,
продлив ее за точку К
Слайд 8Следствие из свойства медианы к гипотенузе. Ключевая задача
Медиана прямоугольного треугольника, проведённая к гипотенузе, делит треугольник на два
равнобедренных треугольника, основаниями которых являются катеты данного треугольникаСлайд 9Использование введения буквенных обозначений величин. Ключевая задача
Если медиана
треугольника равна половине стороны, к которой она проведена, то треугольник
прямоугольный.2α + 2β =180°
α + β =90°
АВС = α + β = 90°
∆ABD и ∆ BCD – равнобедренные
BAD =ABD = α; DBC = BCD = β
Слайд 10Метод вспомогательных построений
При решении некоторых задач удобно в
прямоугольном треугольнике выделять треугольник, образованный медианой и высотой к
гипотенузеСлайд 11Применение свойства медианы к гипотенузе
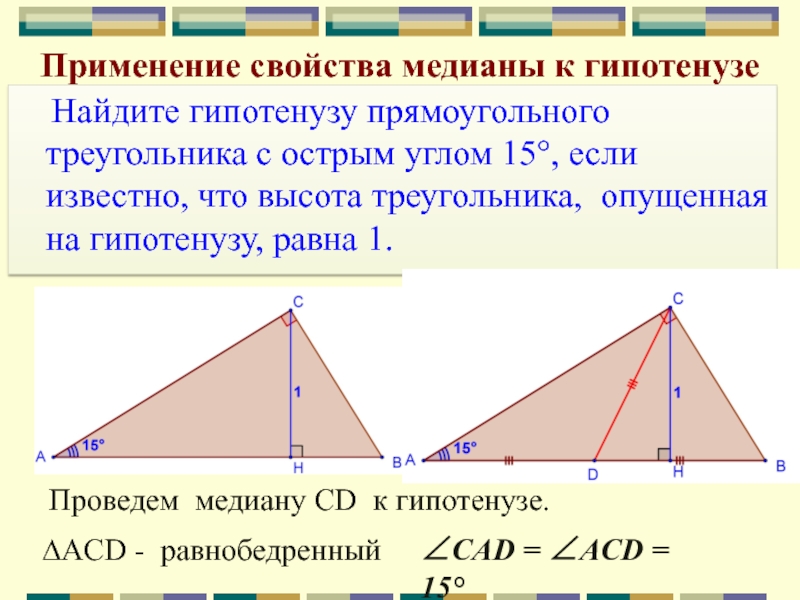
Найдите гипотенузу прямоугольного треугольника
с острым углом 15°, если известно, что высота треугольника, опущенная
на гипотенузу, равна 1.Проведем медиану CD к гипотенузе.
∆ACD - равнобедренный
CAD = ACD = 15°
Слайд 12 Найдите гипотенузу прямоугольного треугольника с острым углом 15°,
если известно, что высота треугольника, опущенная на гипотенузу, равна 1.
CAD = ACD = 15°
CDH = 30° как внешний угол
CD = 2СН = 2
АВ = 2СD = 4
Ответ: 4
Применение свойства медианы к гипотенузе
Слайд 13 Найдите острые углы прямоугольного треугольника, если его гипотенуза
равна 12, а площадь равна 18.
СD = 6
CDH
= 30° CAD = ACD = 15°
CВА = 90° - 15° = 75°
Ответ: 15°; 75°
Применение свойства медианы к гипотенузе
Проведем медиану CD и высоту СН к гипотенузе.
Слайд 14Свойства площади треугольника
Площади треугольников, имеющих общую высоту (равные высоты)
, относятся как стороны, к которым эти высоты проведены
2. Медиана
делит треугольник на два равновеликих треугольникаКлючевые задачи
Слайд 15Метод вспомогательных построений.
Использование осевой симметрии
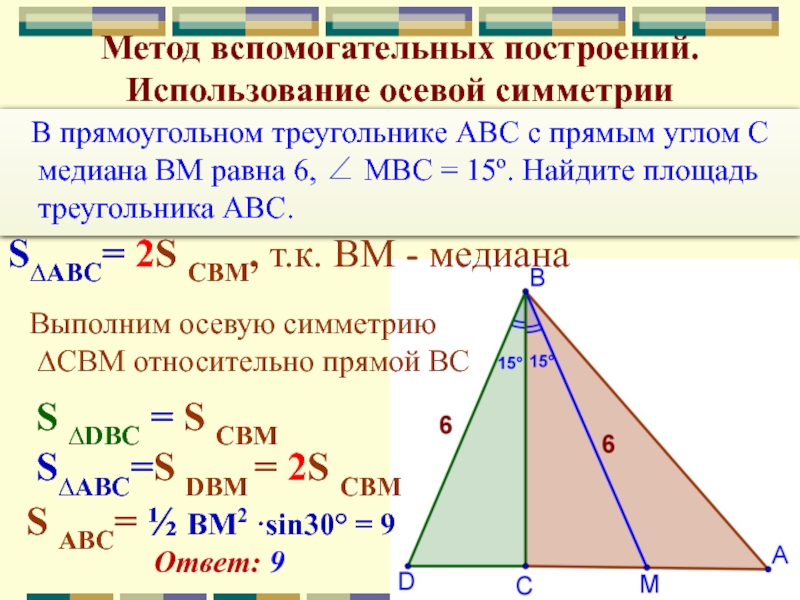
В прямоугольном треугольнике ABC
c прямым углом С медиана BM равна 6, ∠ MBC
= 15º. Найдите площадь треугольника ABC.Выполним осевую симметрию
∆СВМ относительно прямой ВС
S∆АВС= 2S CBМ, т.к. ВМ - медиана
S ∆DВC = S CBМ
S∆АВС=S DBМ = 2S CBМ
S ABC= ½ ВМ2 ·sin30° = 9
Ответ: 9
Слайд 16Построение вспомогательных отрезков в трапеции
Прямая, параллельная
одной из диагоналей трапеции
Прямая, параллельная одной из боковых сторон трапеции
Прямая,
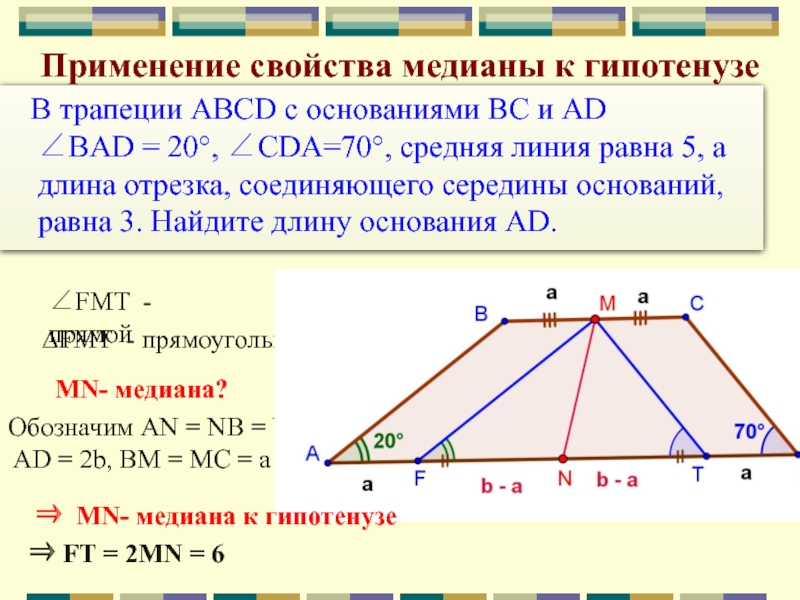
параллельная обеим боковым сторонам трапецииСлайд 17 В трапеции ABCD с основаниями BC и AD
∠BAD = 20°, ∠CDA=70°, средняя линия равна 5, а длина отрезка, соединяющего середины оснований, равна 3. Найдите длину основания AD.
Медиана прямоугольного треугольника к гипотенузе
Построим MF ║AB, MT ║ CD
AD – большее основание
Слайд 18 В трапеции ABCD с основаниями BC и AD
∠BAD = 20°, ∠CDA=70°, средняя линия равна 5, а длина отрезка, соединяющего середины оснований, равна 3. Найдите длину основания AD.
FMT - прямой
∆FMT - прямоугольный
MN- медиана?
Обозначим AN = NB = b;
AD = 2b, BM = MC = a
MN- медиана к гипотенузе
FT = 2MN = 6
Применение свойства медианы к гипотенузе
Слайд 19 В трапеции ABCD с основаниями BC и AD
∠BAD = 20°, ∠CDA=70°, средняя линия равна 5, а длина отрезка, соединяющего середины оснований, равна 3. Найдите длину основания AD.
Медиана прямоугольного треугольника к гипотенузе
MN- медиана к гипотенузе
FT = 2MN = 6
FT = 2b – 2a = 6
средняя линия KL
AD = 2b = 8
Ответ: 8
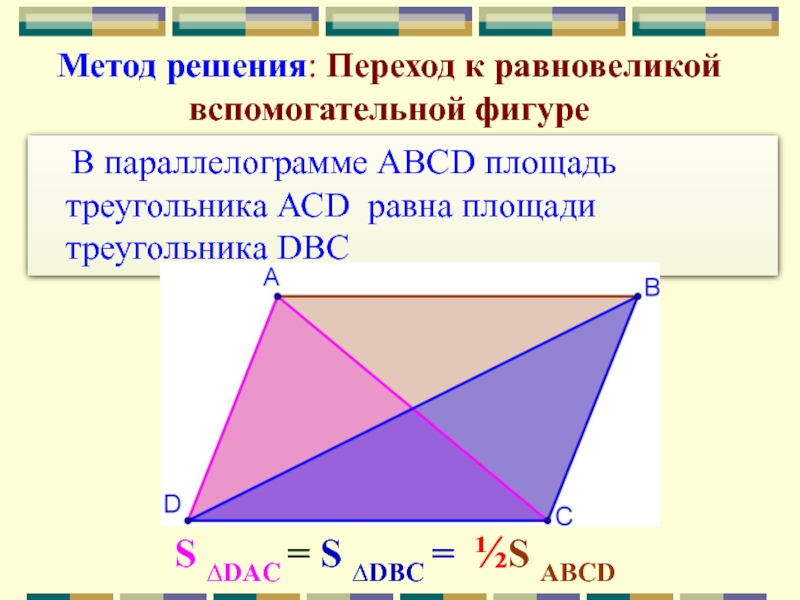
Слайд 20 В параллелограмме ABCD площадь треугольника АСD равна площади
треугольника DBС
Метод решения: Переход к равновеликой вспомогательной фигуре
S ∆DAC =
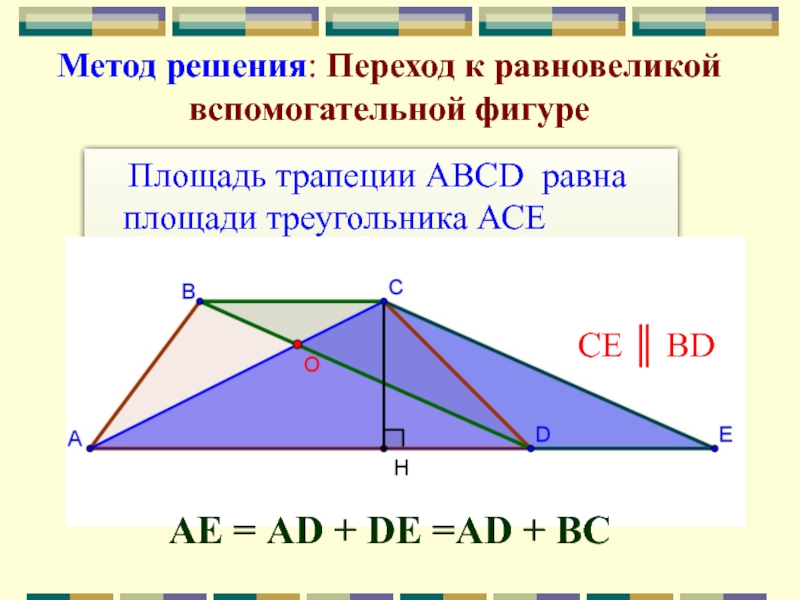
S ∆DВC = ½S ABCDСлайд 21 Площадь трапеции АВСD равна площади треугольника АСЕ
Метод решения:
Переход к равновеликой вспомогательной фигуре
АЕ = AD + DE =AD
+ ВС CE ║ BD
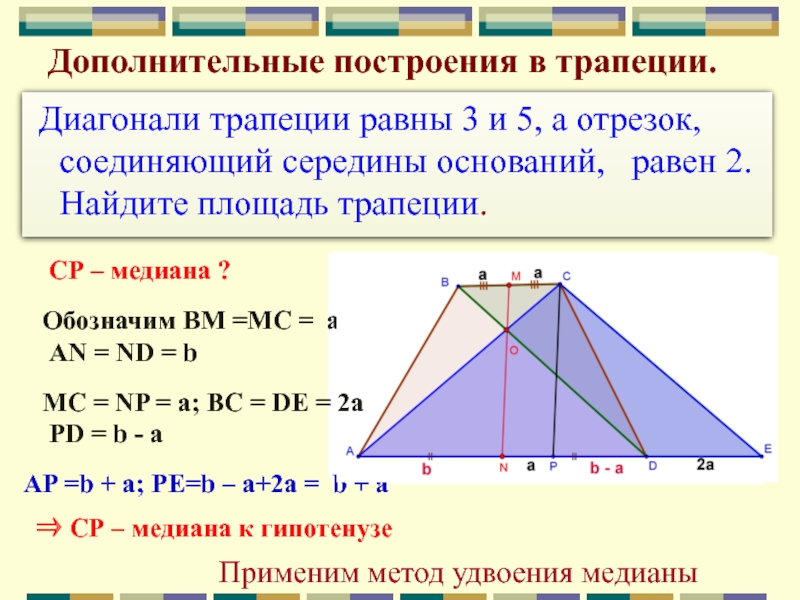
Слайд 22Дополнительные построения в трапеции.
Диагонали трапеции равны 3 и 5, а отрезок, соединяющий
середины оснований, равен 2. Найдите площадь трапеции. Проведем CE ║ BD, СР ║MN
S ABCD = S ∆АCЕ
Переход к равновеликой вспомогательной фигуре
Слайд 23 Диагонали трапеции равны 3 и 5, а отрезок, соединяющий
середины оснований, равен 2. Найдите площадь трапеции.
СР – медиана
?Обозначим ВМ =MC = а;
АN = ND = b
AP =b + а; PE=b – a+2a = b + a
СР – медиана к гипотенузе
MC = NP = а; BC = DE = 2a
PD = b - a
Дополнительные построения в трапеции.
Применим метод удвоения медианы
Слайд 24Дополнительные построения в трапеции. Метод удвоения медианы. Переход к
равновеликой фигуре
Диагонали
трапеции равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найдите площадь трапеции. СН=2СР= 4
S ∆CНЕ = S ∆АCЕ = SABCD
∆СНЕ - прямоугольный, СНЕ = 90°
СН= 4; СЕ = 5; НЕ = 3
S ABCD = S ∆АCЕ =S∆СНЕ= ½ СН ·НЕ = ½·4 · 3 = 6
Ответ: 6
Слайд 25Метод площадей
Идея метода: площади фигуры находим, используя
различные формулы или различные отрезки и углы. Приравняв эти выражения,
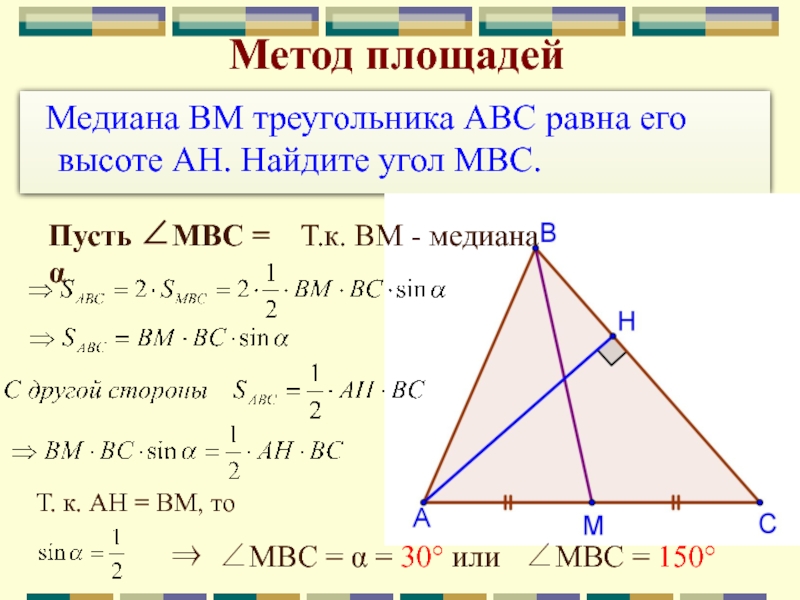
получаем уравнение, содержащее известные и искомые величины.Слайд 26 Медиана BM треугольника ABC равна его высоте AH. Найдите
угол MBC.
Метод площадей
Пусть МВС = α
Т. к. АН = ВМ,
то МВС = α = 30° или МВС = 150°
Т.к. ВМ - медиана
Слайд 28 В треугольник вписана окружность радиуса 4. Одна из сторон
треугольника разделена точкой касания на части, равные 6 и 8.
Найдите две другие стороны треугольника.Метод площадей
Обозначим AM = AN = x
х = 7
S△ABC = (8 + 6 + x) · 4 = (14 + x) · 4.
С другой стороны, по формуле Герона
AC = x + 6 = 13,
AB = x + 8 = 15
Ответ: 13; 15
Слайд 29Метод решения: Введение вспомогательной окружности
Идея метода: ввести
в рассмотрение окружность, если это возможно в данной конфигурации, чтобы
применить разнообразные свойства отрезков и углов, связанных с нейСлайд 30Введение вспомогательной окружности
В выпуклом четырехугольнике ABCD ∠ BCA =
20º, ∠ BAC =
35º, ∠ BDС = 70º, ∠ BDA = 40º. Найдите углы между диагоналями этого четырехугольника.20º =½· 40º
Можно построить окружность с центром в точке D, проходящую через остальные три вершины четырехугольника С; В и D
∠ BCA и ∠ BCA опираются на отрезок ВА и лежат от него по одну сторону
Слайд 31Введение вспомогательной окружности
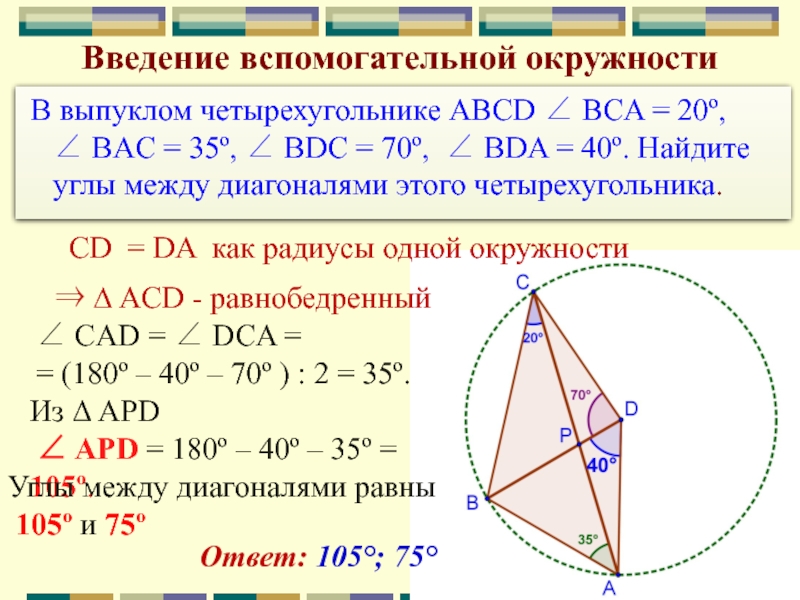
∠ СAD = ∠ DСA =
= (180º –
40º – 70º ) : 2 = 35º.
Из Δ APD
∠ APD = 180º – 40º – 35º = 105º.
Углы между диагоналями равны
105º и 75º
Ответ: 105°; 75°
∆ ACD - равнобедренный
В выпуклом четырехугольнике ABCD ∠ BCA = 20º, ∠ BAC = 35º, ∠ BDС = 70º, ∠ BDA = 40º. Найдите углы между диагоналями этого четырехугольника.
CD = DA как радиусы одной окружности
Слайд 32Введение вспомогательной окружности
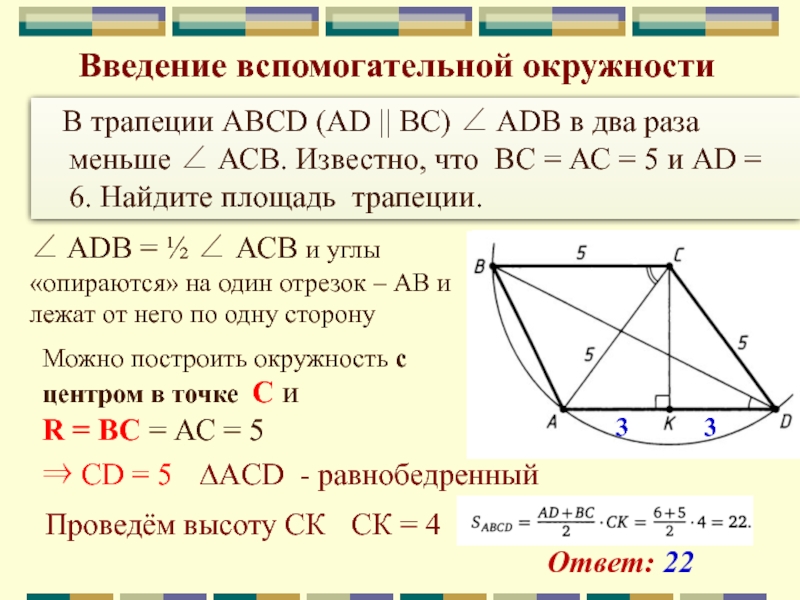
В трапеции ABCD (AD || ВС)
ADB в два раза меньше АСВ. Известно, что
ВС = АС = 5 и AD = 6. Найдите площадь трапеции. ADB = ½ АСВ и углы «опираются» на один отрезок – АВ и лежат от него по одну сторону
Можно построить окружность с центром в точке С и R = ВС = АС = 5
CD = 5
∆ACD - равнобедренный
Проведём высоту СК
CК = 4
Ответ: 22
3
3