Слайд 1 Параллельная обработка больших графов
www.dislab.org
Александр Сергеевич Семенов
Слайд 2Откуда возникают большие графы?
Интернет (WWW)
На сентябрь 2016 – 47
миллиардов страниц
По оценке Google – более 1 триллиона
Социальные медиа
Блогосфера: 2011
– 172 х 106 (+106/день)
Facebook: 2010 – 500 х 106, 2013 – 1:1 х 109 (650 х 106 акт.польз./день), 140 х 109 связей
LinkedIn: 2013 – 8 х 106, 60 х 106 связей
Twitter: 2011 – 140 х 106 сообщений/день
Транспортные сети
Биоинформатика
Бизнес-задачи
1http://www.worldwidewebsize.com
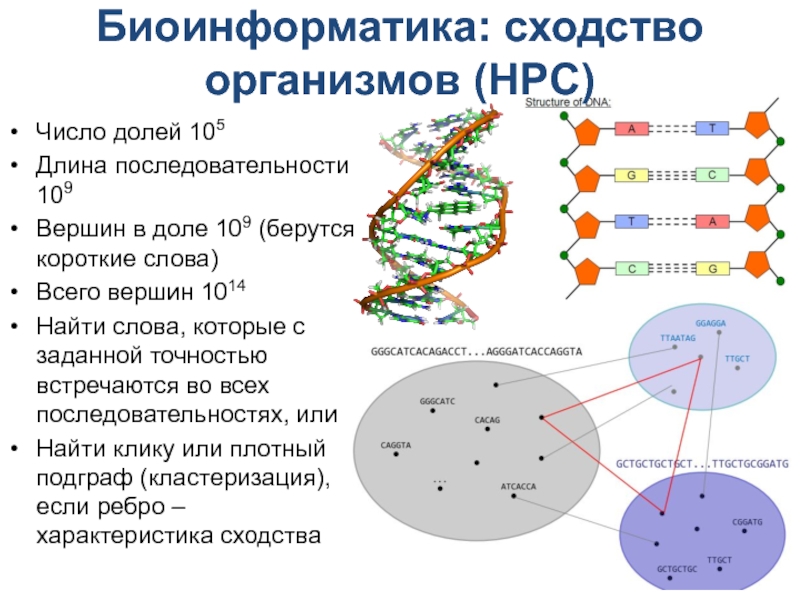
Слайд 3Биоинформатика: сходство организмов (HPC)
Число долей 105
Длина последовательности 109
Вершин в
доле 109 (берутся короткие слова)
Всего вершин 1014
Найти слова, которые с
заданной точностью встречаются во всех последовательностях, или
Найти клику или плотный подграф (кластеризация), если ребро – характеристика сходства
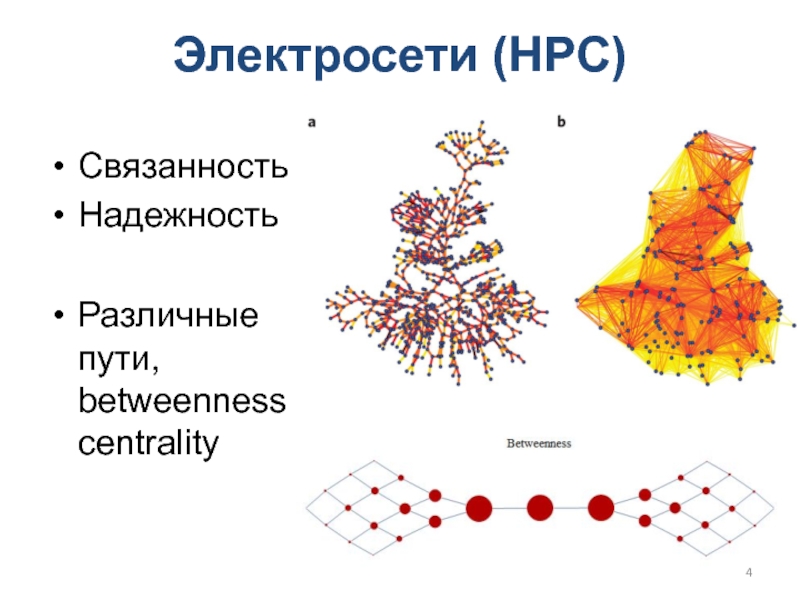
Слайд 4Электросети (HPC)
Связанность
Надежность
Различные пути, betweenness centrality
Слайд 5Анализ социальных сетей (HPC)
Анализ сообществ
Понимание намерений
Динамика популяции
Распространение эпидемий
Кластеризация
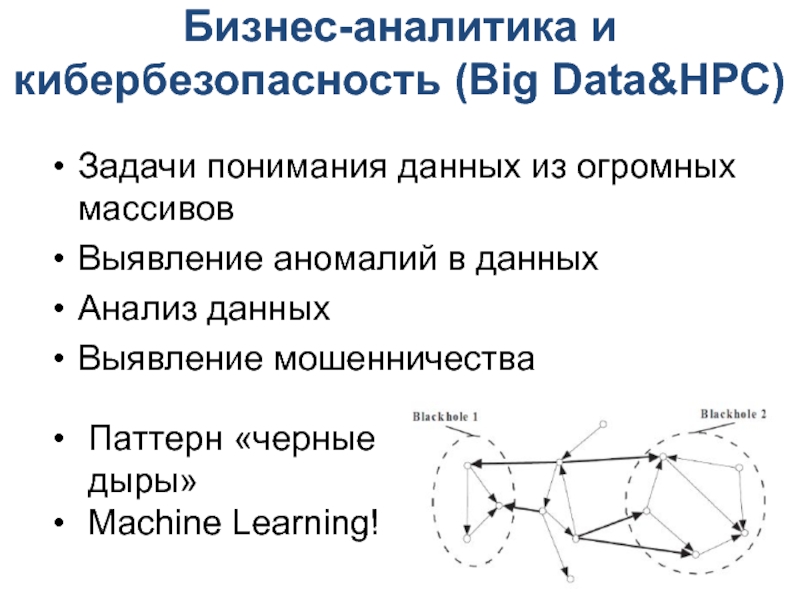
Слайд 6Бизнес-аналитика и кибербезопасность (Big Data&HPC)
Задачи понимания данных из огромных массивов
Выявление
аномалий в данных
Анализ данных
Выявление мошенничества
Паттерн «черные дыры»
Machine Learning!
Слайд 7Признаки в графах для машинного обучения
Вершины (степень, полустепени, betweenness centrality,
PageRank)
Пары вершин (количество общих соседей, вес ребра)
Egonet (количество треугольников, количество
ребер)
Группа вершин (плотность = кол-во ребер/кол-во вершин, общий вес ребер)
Слайд 8Классификация задач анализа графов
По типу графов
статические графы (static graph analysis)
динамические
графы (dynamic graph analysis)
обработка потоков вершин и ребер (streaming graph
analysis)
По типу обработки
в режиме реального времени (online)
в режиме выполнения заданий (offline, batch processing)
Слайд 9Программные модели и средства
Реляционная модель
Cassandra, SAP HANA, …
MapReduce
Generic MR:
Hadoop,
Yarn, Dryad, Stratosphere, Haloop
Graph-optimized: Pegasus, Surfer, GBASE, GraphX
Специализированные языки программирования
Проблемно-ориентированные
языки программирования (DSL)
Green-Marl, Exedra
Языки запросов к графовым СУБД
SPARQL, G-SPARQL, Cypher (Neo4j), …
BSP
Parallel BGL
Vertex-centric/BSP
Pregel (Giraph, Hama, Mizan, …)
Vertex-centric/Data, Message-driven
GraphLab, SWARM, Trinity, Charm++, …
Fine-grained Threaded Shared Memory/PGAS
GraphCT, STINGER, Grappa
Технологии параллельного программирования
OpenMP, MPI, CUDA, …
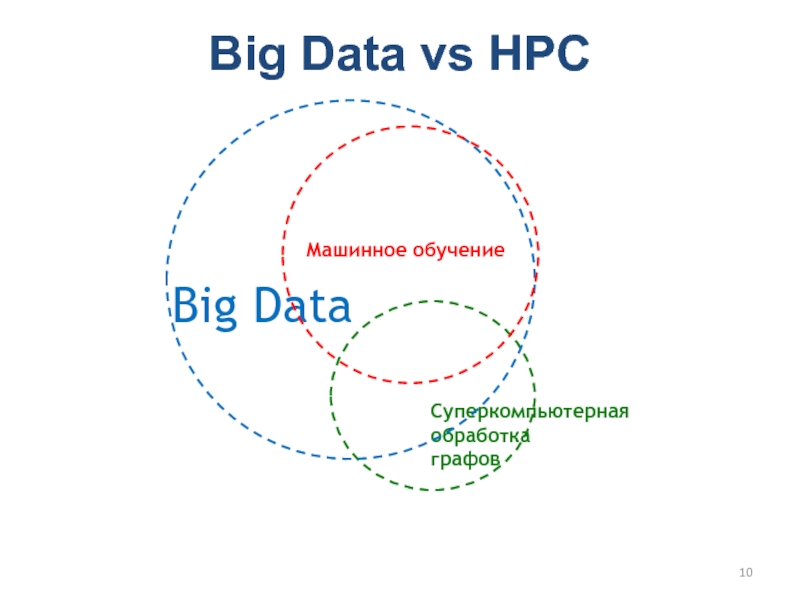
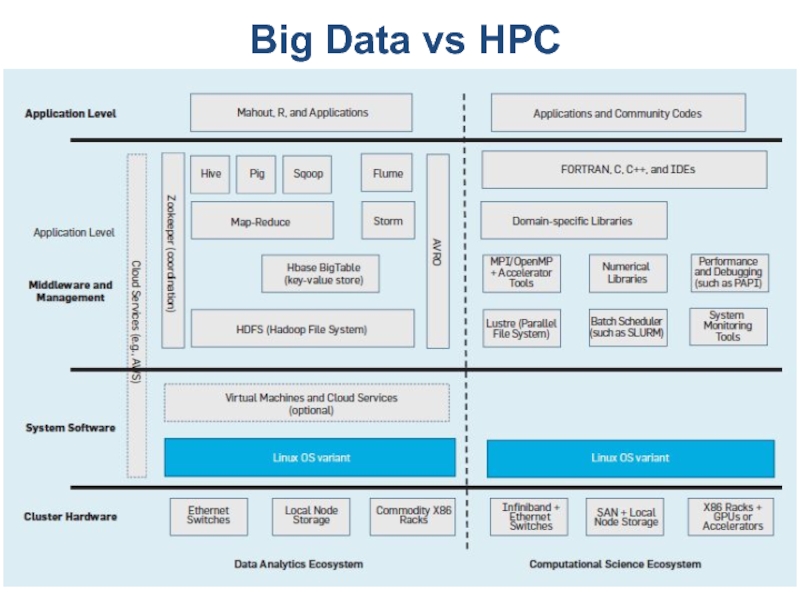
Слайд 10Big Data vs HPC
Машинное обучение
Слайд 12План
Виды графов
Основные проблемы, возникающие при решении задач обработки графов
Подходы к
решению задач в рамках одного вычислительного узла
Подходы к решению задач
в рамках распределенной вычислительной системы
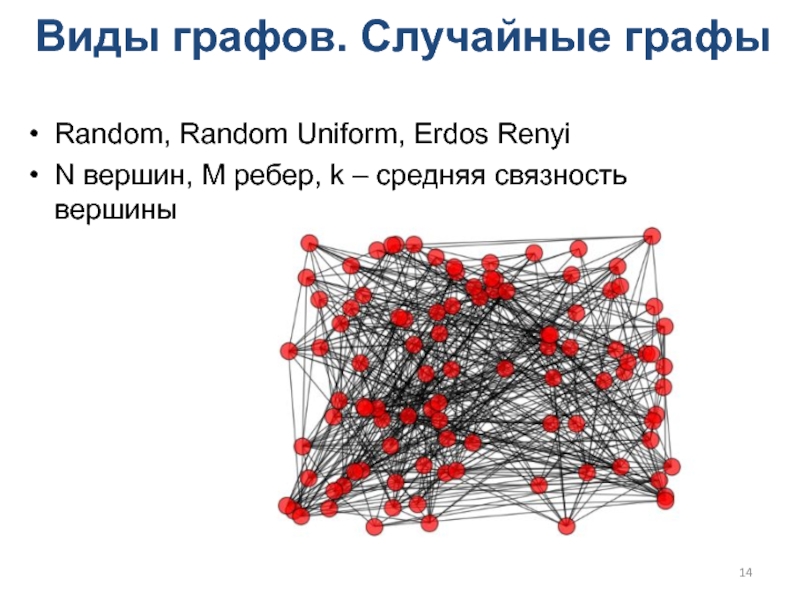
Слайд 14Виды графов. Случайные графы
Random, Random Uniform, Erdos Renyi
N вершин, M
ребер, k – средняя связность вершины
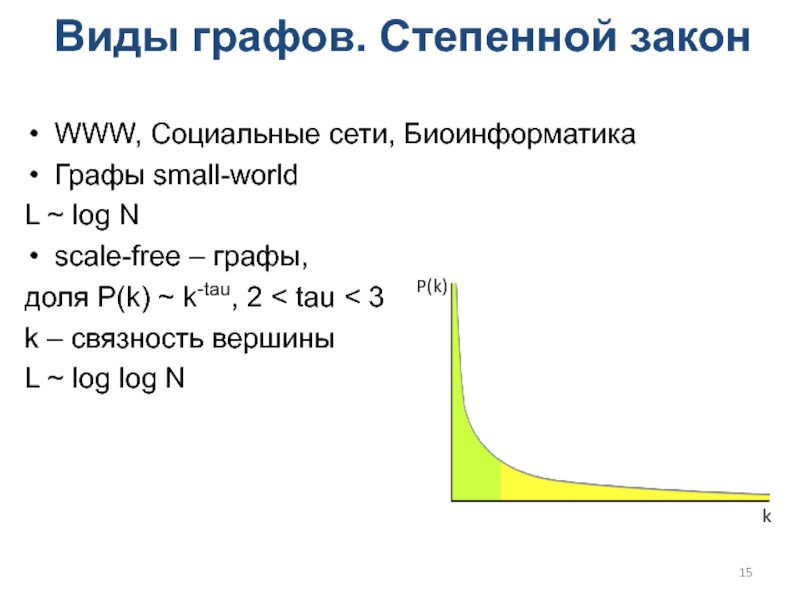
Слайд 15Виды графов. Степенной закон
WWW, Социальные сети, Биоинформатика
Графы small-world
L ~ log
N
scale-free – графы,
доля P(k) ~ k-tau, 2 < tau
3
k – связность вершины
L ~ log log N
k
P(k)
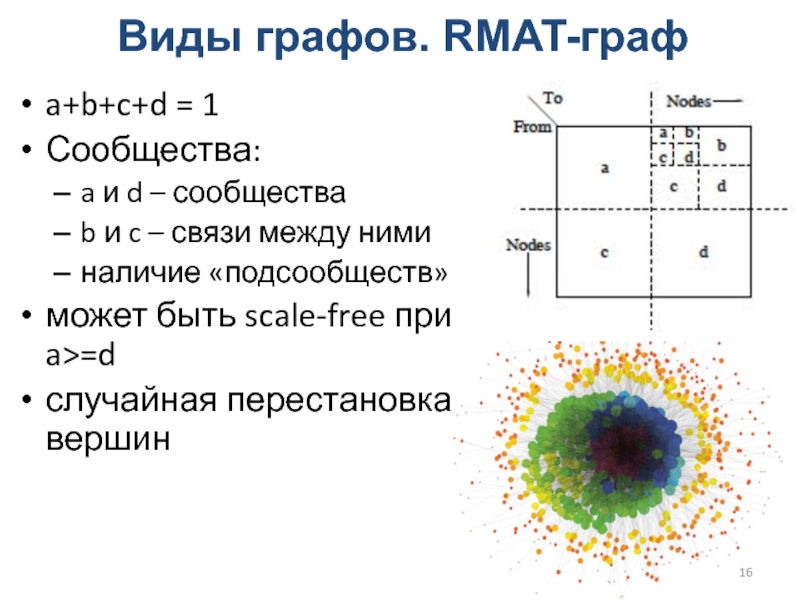
Слайд 16Виды графов. RMAT-граф
a+b+c+d = 1
Сообщества:
a и d – сообщества
b и
c – связи между ними
наличие «подсообществ»
может быть scale-free при a>=d
случайная
перестановка вершин
Слайд 17Виды графов. LFR*-граф
Параметры:
mu ∈ [0;1], показывает количество связей вне
сообщества
com_tau – показатель степени в законе распределения размеров сообществ
deg_tau
– показатель степени в законе распределения степеней вершин
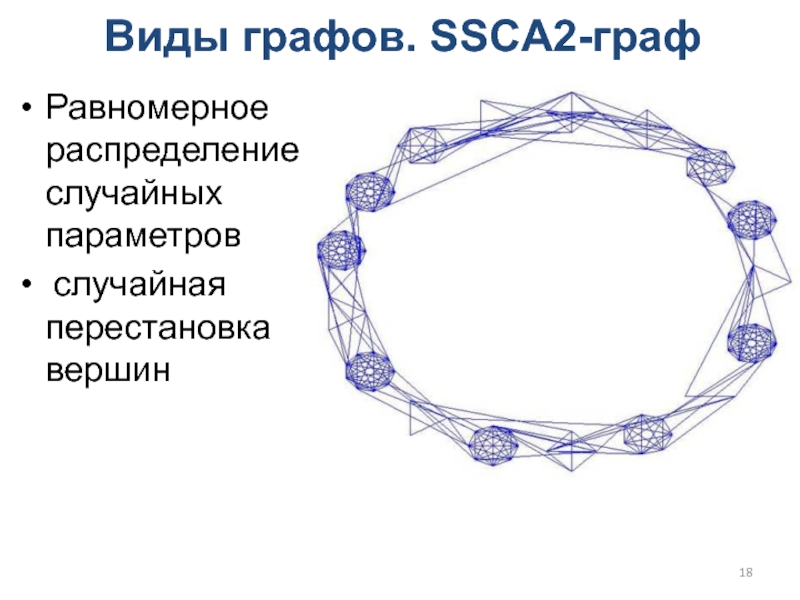
Слайд 18Виды графов. SSCA2-граф
Равномерное распределение случайных параметров
случайная перестановка вершин
Слайд 19Основные проблемы, возникающие при решении задач обработки графов
Слайд 20Проблемы анализа больших графов
Data-driven computations. Зависимость вычислений от данных (топологии
графа). Невозможность применения методов статического распараллеливания вычислений.
Unstructured problems. Работа с
нерегулярными, неструктурированными данными, трудность распараллеливания.
Poor locality. Низкая пространственно-временная локализация обращений к памяти.
High data access to computation ratio. Преобладание команд доступа к памяти над командами выполнения арифметических операций.
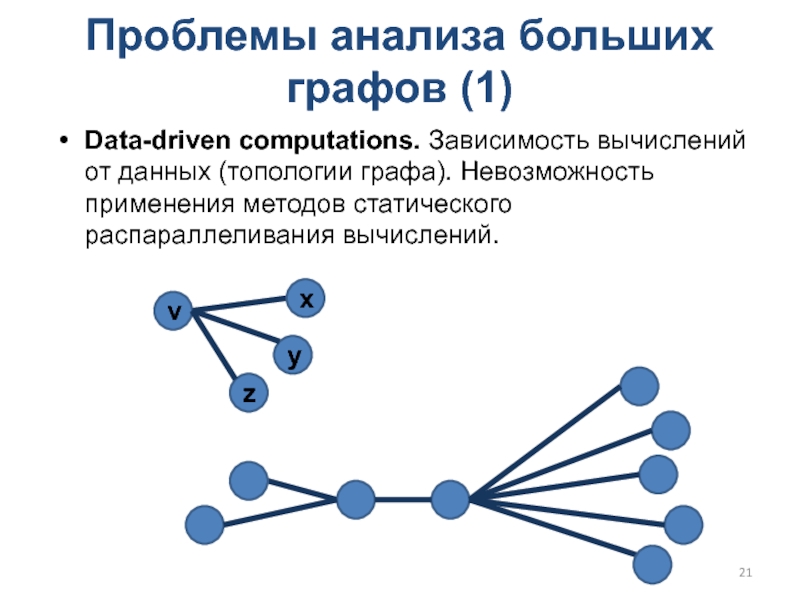
Слайд 21Проблемы анализа больших графов (1)
Data-driven computations. Зависимость вычислений от данных
(топологии графа). Невозможность применения методов статического распараллеливания вычислений.
v
x
y
z
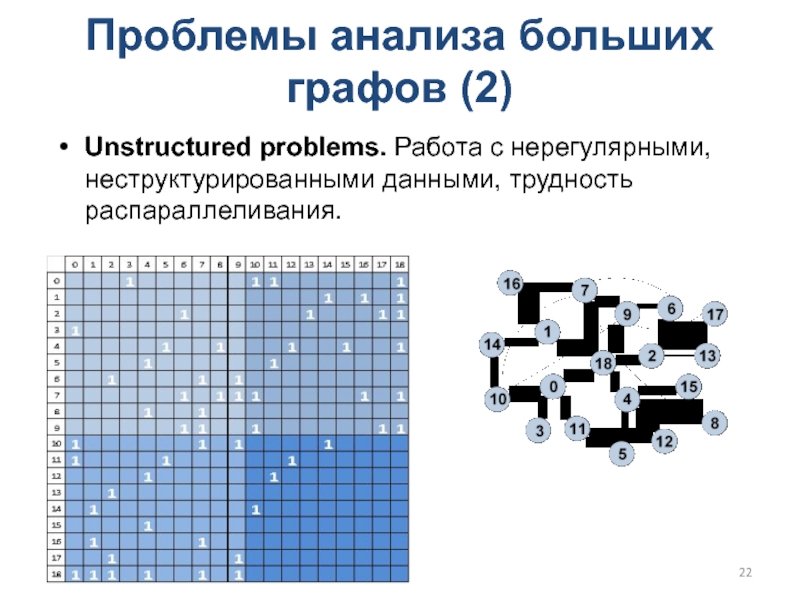
Слайд 22Проблемы анализа больших графов (2)
Unstructured problems. Работа с нерегулярными, неструктурированными
данными, трудность распараллеливания.
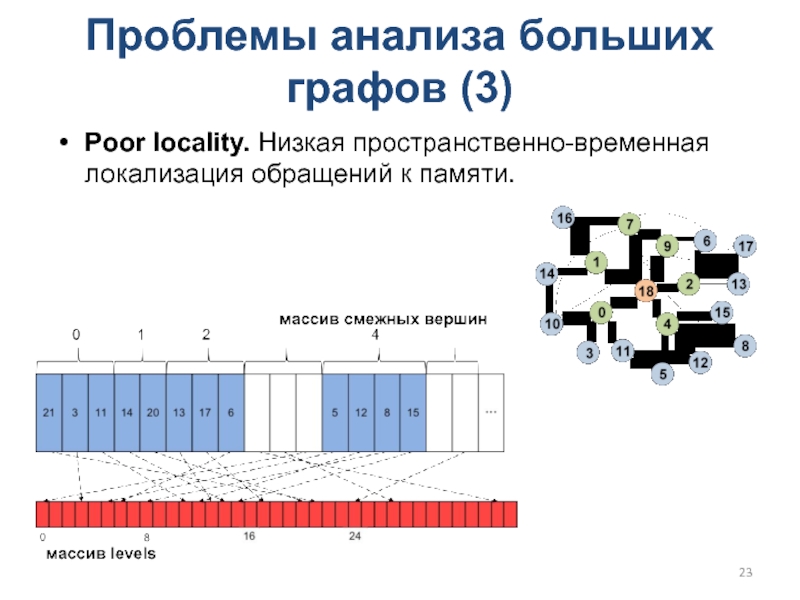
Слайд 23Проблемы анализа больших графов (3)
Poor locality. Низкая пространственно-временная локализация обращений
к памяти.
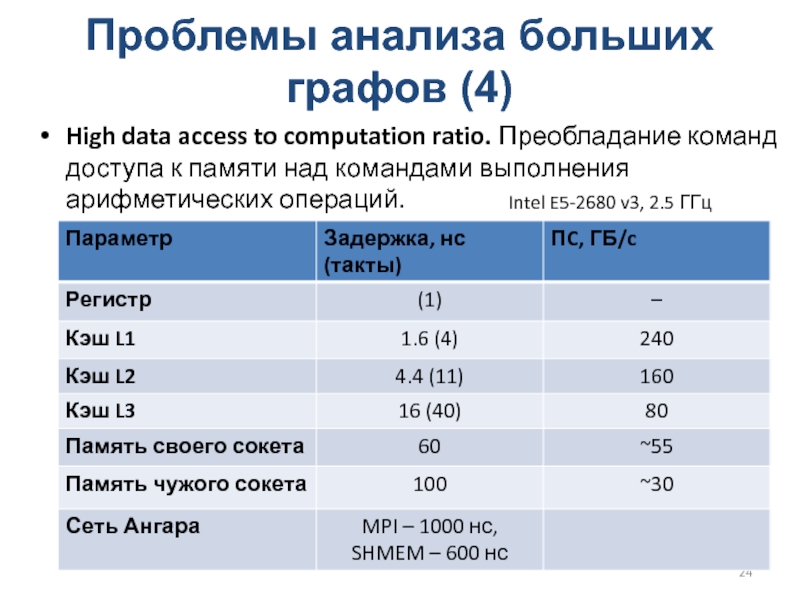
Слайд 24Проблемы анализа больших графов (4)
High data access to computation ratio.
Преобладание команд доступа к памяти над командами выполнения арифметических операций.
Intel
E5-2680 v3, 2.5 ГГц
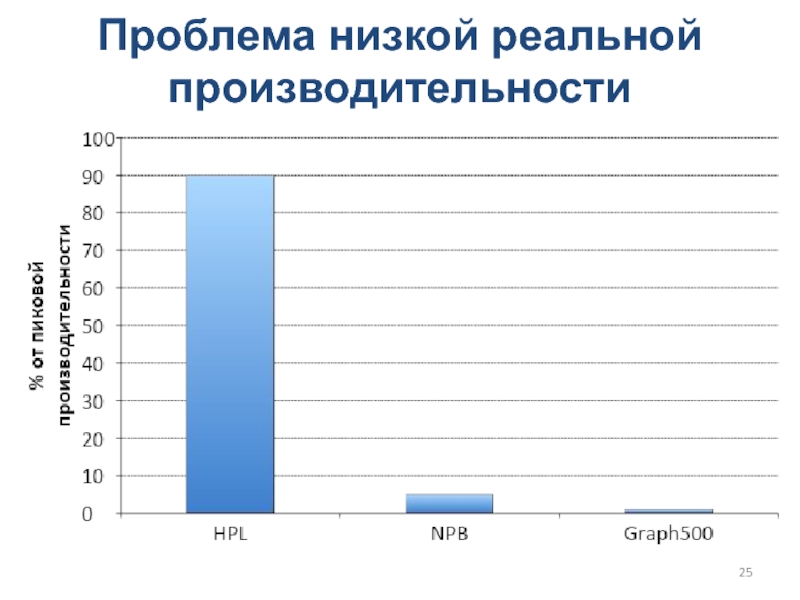
Слайд 25Проблема низкой реальной производительности
Слайд 26Проблемы и подходы к решению задач обработки графов в рамках
одного вычислительного узла
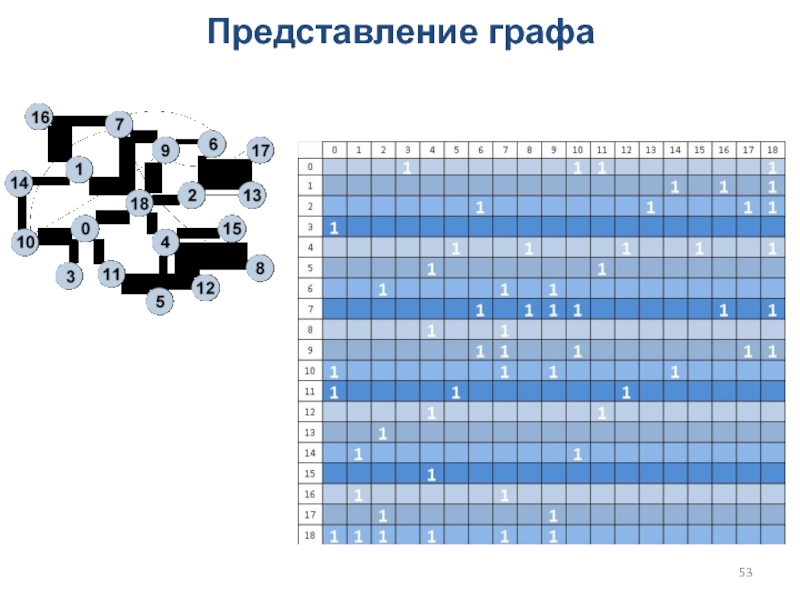
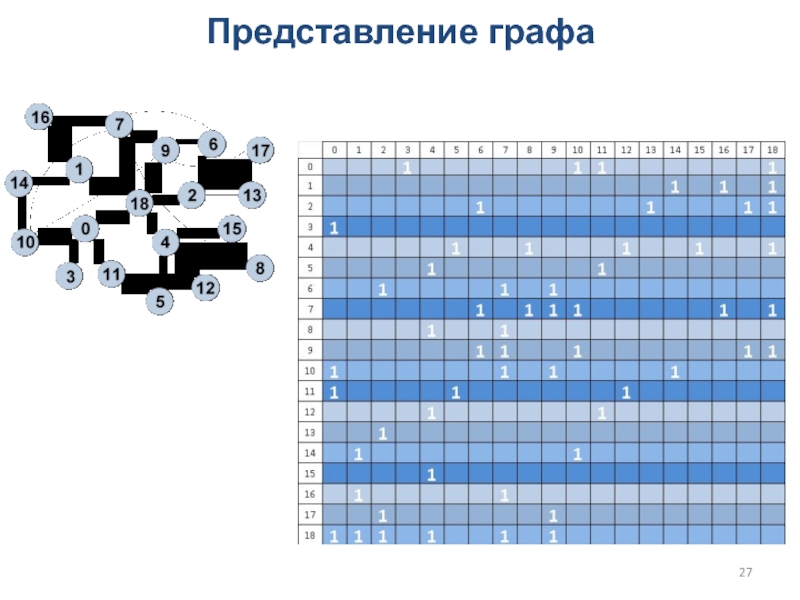
Слайд 28Форматы представления разреженных матриц
Доля ненулевых элементов мала
Можно хранить только
позиции и значения ненулевых элементов
Compressed Row Storage (CRS)
Coordinate list (COO)
DIA
ELLPACK
SELLPACK
Оптимизированный
под задачу
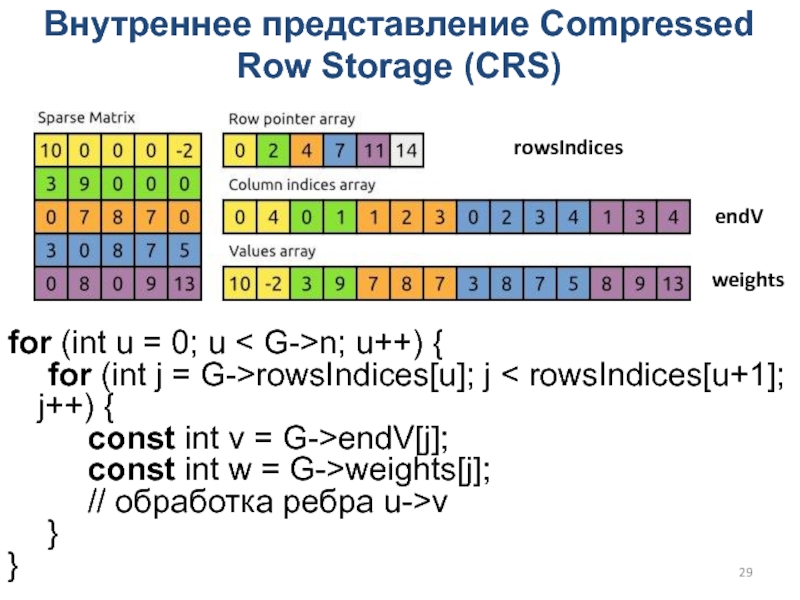
Слайд 29Внутреннее представление Compressed Row Storage (CRS)
for (int u = 0;
u < G->n; u++) {
for (int j = G->rowsIndices[u]; j
< rowsIndices[u+1]; j++) {
const int v = G->endV[j];
const int w = G->weights[j];
// обработка ребра u->v
}
}
rowsIndices
endV
weights
Слайд 30Coordinate list (COO)
Sparse matrix
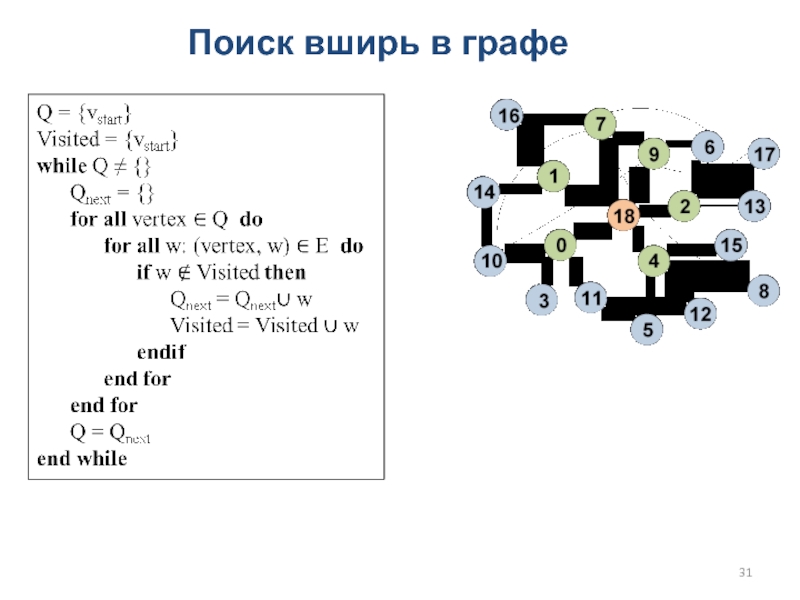
Слайд 32Поиск вширь в графе (BFS)
Подход Queue-based, алгоритм simple
Qcounter = 1
Q[0] = root
Visited[root] = 1
while Qcounter > 0
Qnext_counter = 0
#pragma omp parallel for
for all vertex ∈ Q do
for all w: (vertex, w) ∈ E do
if Visited[w] == 0 then
Qnext[__sync_fetch_and_add(Qnext_counter, 1)] = w
Visited[w] = 1
endif
end for
end for
swap(Q, Qnext) // обмен Q и Qnext
end while
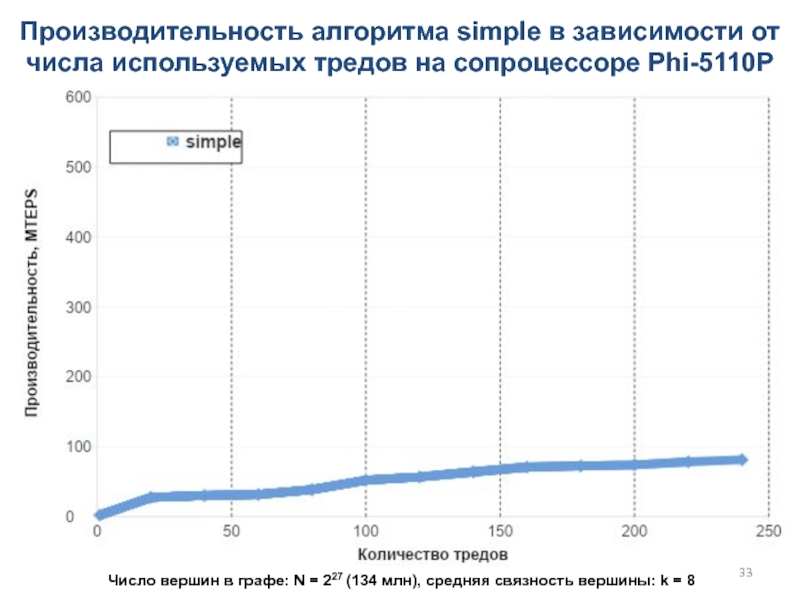
Слайд 33Производительность алгоритма simple в зависимости от числа используемых тредов на
сопроцессоре Phi-5110P
Число вершин в графе: N = 227 (134 млн),
cредняя связность вершины: k = 8
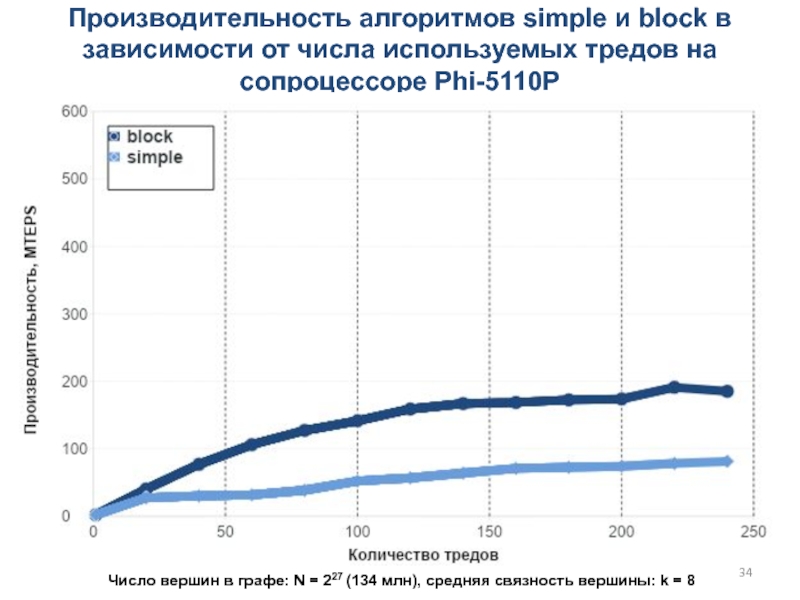
Слайд 34Производительность алгоритмов simple и block в зависимости от числа используемых
тредов на сопроцессоре Phi-5110P
Число вершин в графе: N = 227
(134 млн), cредняя связность вершины: k = 8
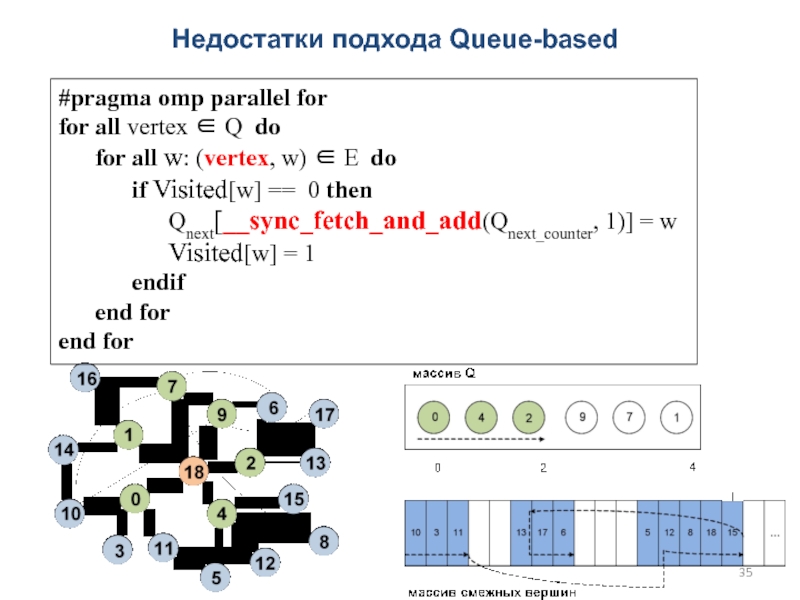
Слайд 35Недостатки подхода Queue-based
#pragma omp parallel for
for all vertex ∈ Q
do
for all w: (vertex, w) ∈ E
do
if Visited[w] == 0 then
Qnext[__sync_fetch_and_add(Qnext_counter, 1)] = w
Visited[w] = 1
endif
end for
end for
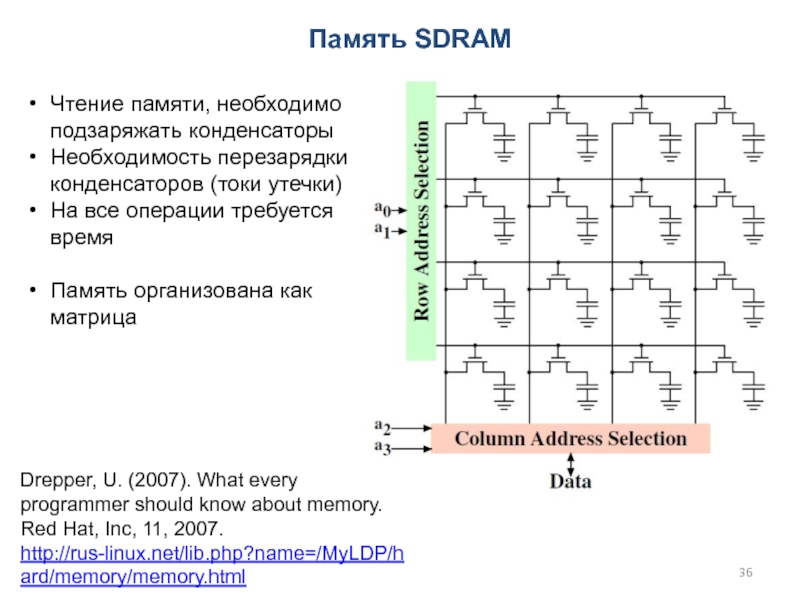
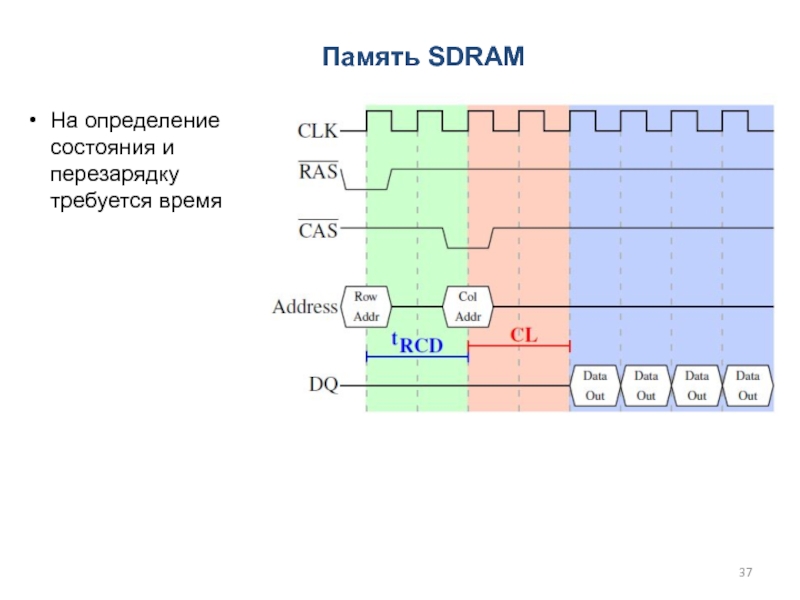
Слайд 36Память SDRAM
Чтение памяти, необходимо подзаряжать конденсаторы
Необходимость перезарядки конденсаторов (токи утечки)
На
все операции требуется время
Память организована как матрица
Drepper, U. (2007). What
every programmer should know about memory. Red Hat, Inc, 11, 2007.
http://rus-linux.net/lib.php?name=/MyLDP/hard/memory/memory.html
Слайд 37На определение состояния и перезарядку требуется время
Память SDRAM
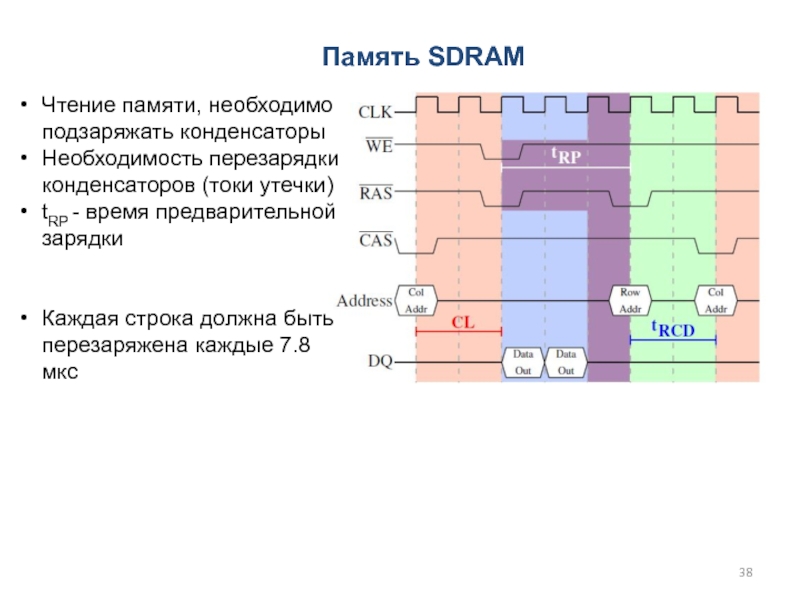
Слайд 38Чтение памяти, необходимо подзаряжать конденсаторы
Необходимость перезарядки конденсаторов (токи утечки)
tRP -
время предварительной зарядки
Каждая строка должна быть перезаряжена каждые 7.8 мкс
Память
SDRAM
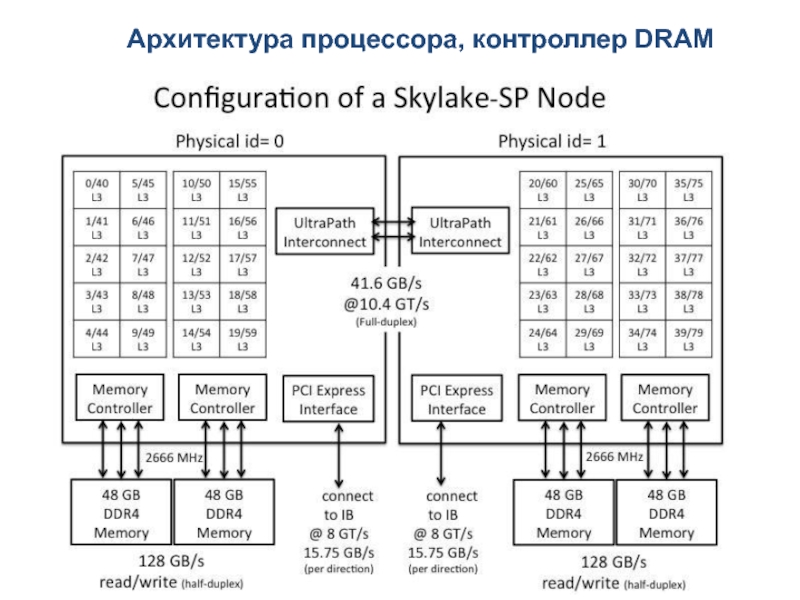
Слайд 39Архитектура процессора, контроллер DRAM
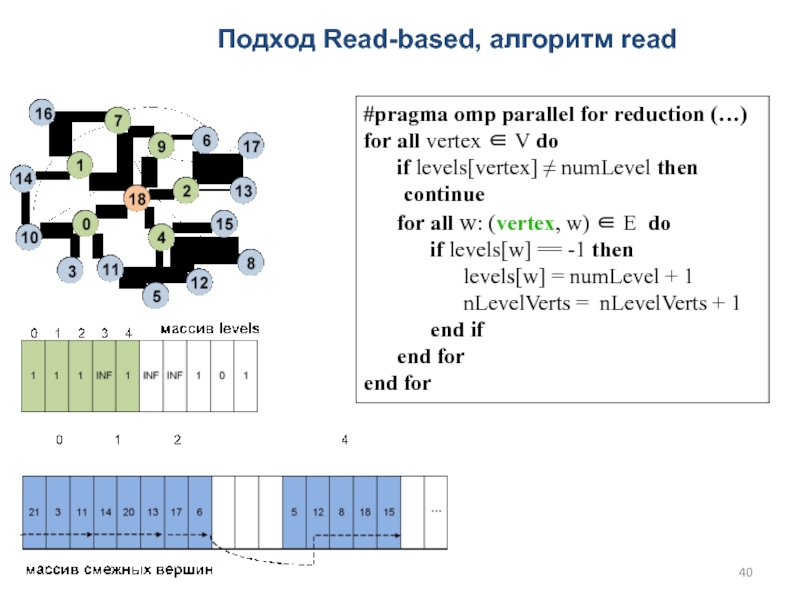
Слайд 40Подход Read-based, алгоритм read
#pragma omp parallel for reduction (…)
for all
vertex ∈ V do
if levels[vertex] ≠ numLevel
then continue
for all w: (vertex, w) ∈ E do
if levels[w] == -1 then
levels[w] = numLevel + 1
nLevelVerts = nLevelVerts + 1
end if
end for
end for
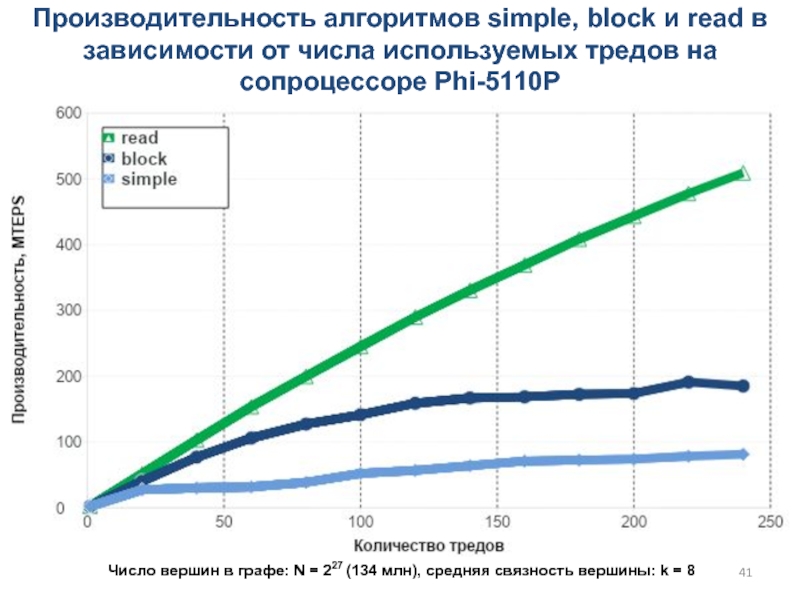
Слайд 41Производительность алгоритмов simple, block и read в зависимости от числа
используемых тредов на сопроцессоре Phi-5110P
Число вершин в графе: N
= 227 (134 млн), cредняя связность вершины: k = 8
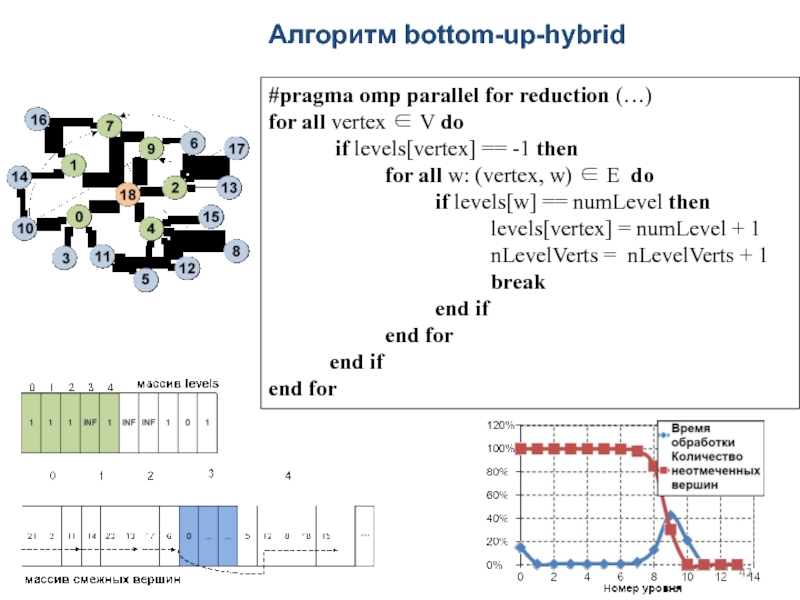
Слайд 42Алгоритм bottom-up-hybrid
#pragma omp parallel for reduction (…)
for all vertex ∈
V do
if levels[vertex] ==
-1 then
for all w: (vertex, w) ∈ E do
if levels[w] == numLevel then
levels[vertex] = numLevel + 1
nLevelVerts = nLevelVerts + 1
break
end if
end for
end if
end for
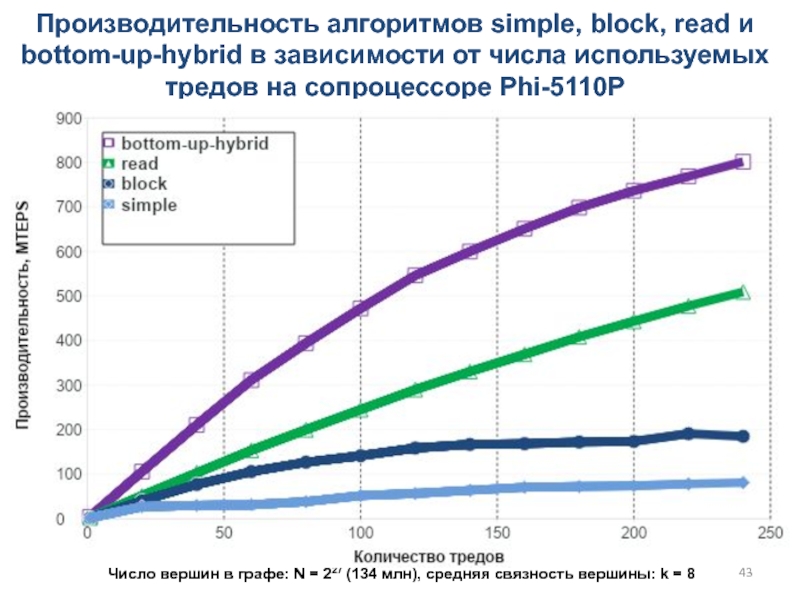
Слайд 43Производительность алгоритмов simple, block, read и bottom-up-hybrid в зависимости от
числа используемых тредов на сопроцессоре Phi-5110P
Число вершин в графе:
N = 227 (134 млн), cредняя связность вершины: k = 8
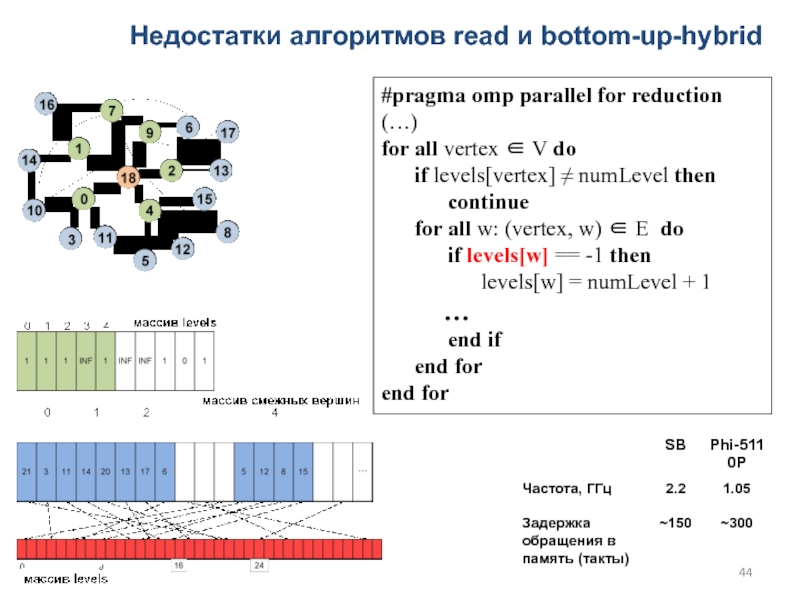
Слайд 44Недостатки алгоритмов read и bottom-up-hybrid
#pragma omp parallel for reduction (…)
for all vertex ∈ V do
if levels[vertex]
≠ numLevel then
continue
for all w: (vertex, w) ∈ E do
if levels[w] == -1 then
levels[w] = numLevel + 1
…
end if
end for
end for
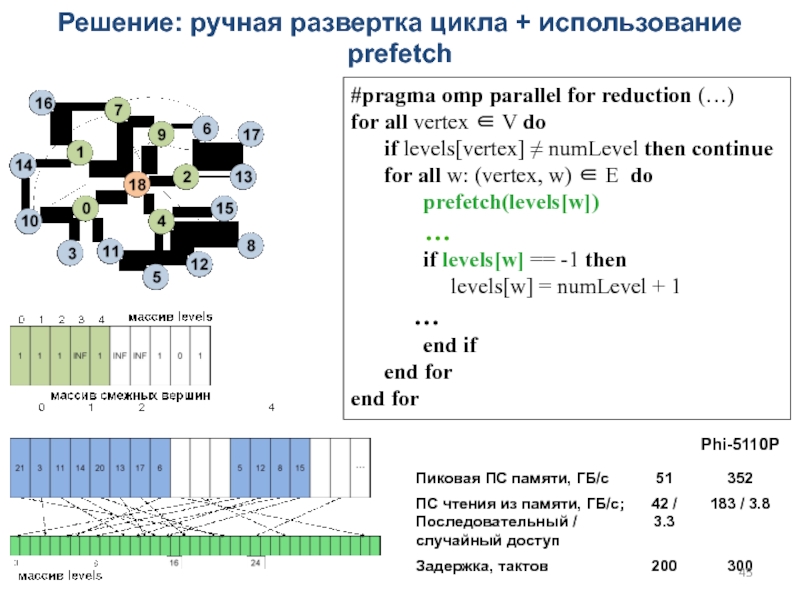
Слайд 45Решение: ручная развертка цикла + использование prefetch
#pragma omp parallel for
reduction (…)
for all vertex ∈ V do
if levels[vertex] ≠ numLevel then continue
for all w: (vertex, w) ∈ E do
prefetch(levels[w])
…
if levels[w] == -1 then
levels[w] = numLevel + 1
…
end if
end for
end for
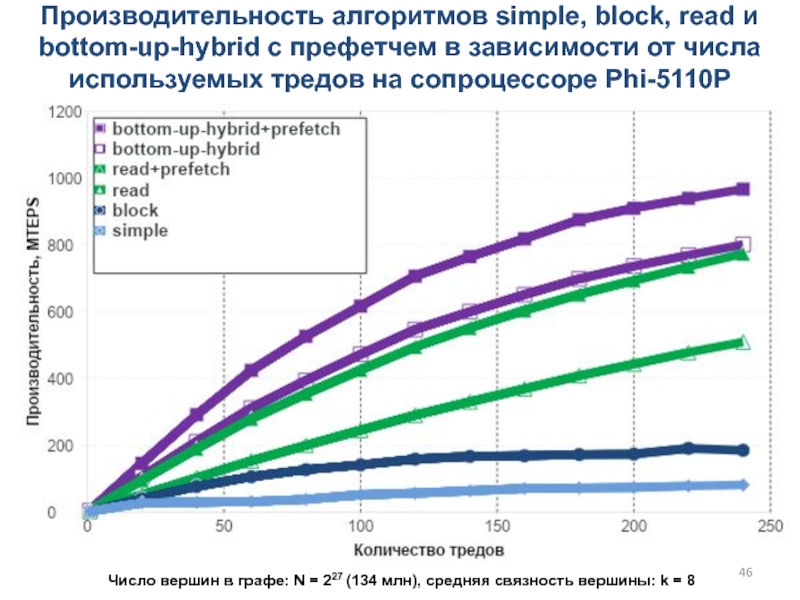
Слайд 46Производительность алгоритмов simple, block, read и bottom-up-hybrid с префетчем в
зависимости от числа используемых тредов на сопроцессоре Phi-5110P
Число вершин в
графе: N = 227 (134 млн), cредняя связность вершины: k = 8
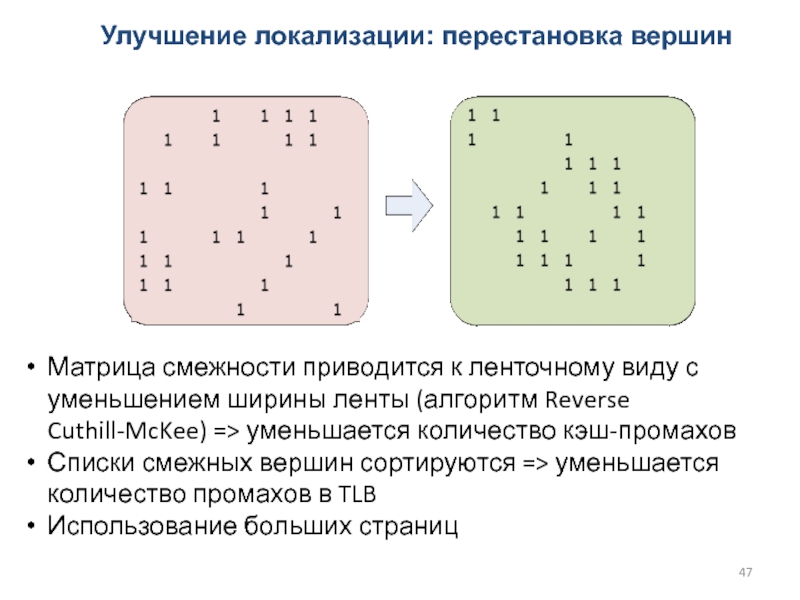
Слайд 47Улучшение локализации: перестановка вершин
Матрица смежности приводится к ленточному виду с
уменьшением ширины ленты (алгоритм Reverse Cuthill-McKee) => уменьшается количество кэш-промахов
Списки
смежных вершин сортируются => уменьшается количество промахов в TLB
Использование больших страниц
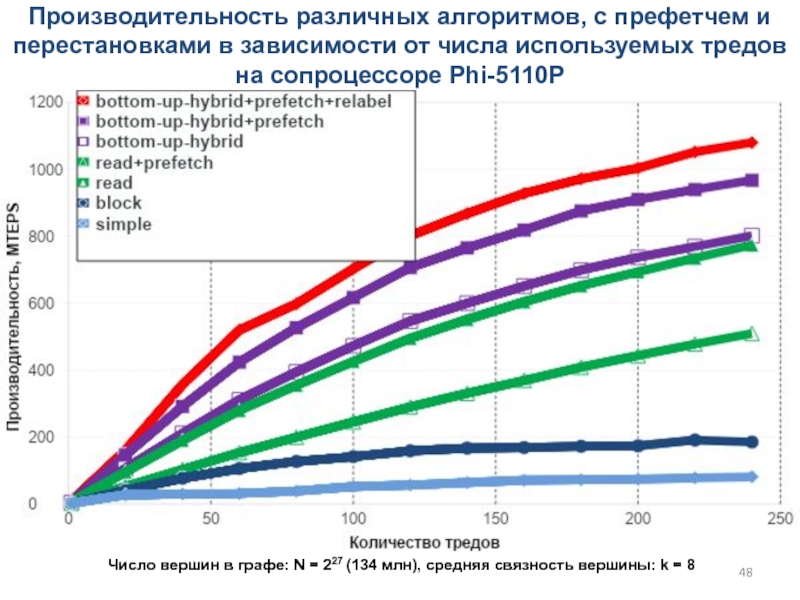
Слайд 48Производительность различных алгоритмов, с префетчем и перестановками в зависимости от
числа используемых тредов на сопроцессоре Phi-5110P
Число вершин в графе: N
= 227 (134 млн), cредняя связность вершины: k = 8
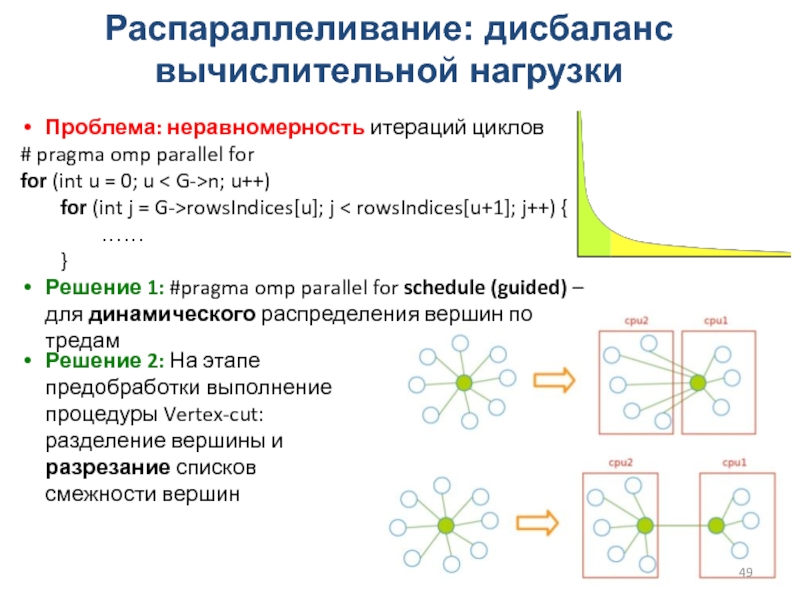
Слайд 49Распараллеливание: дисбаланс вычислительной нагрузки
Проблема: неравномерность итераций циклов
# pragma omp parallel
for
for (int u = 0; u < G->n; u++)
for
(int j = G->rowsIndices[u]; j < rowsIndices[u+1]; j++) {
……
}
Решение 1: #pragma omp parallel for schedule (guided) – для динамического распределения вершин по тредам
Решение 2: На этапе предобработки выполнение процедуры Vertex-cut: разделение вершины и разрезание списков смежности вершин
Слайд 50Проблема: постоянная смена данных в кэше, низкие характеристики при случайном
доступе
Решения на этапе предобработки:
Хранение только половины графа (для неориентированного)
Удаление кратных
ребер
Перестановка вершин (Cuthill-McKee)
Сжатие данных
edge_id_t: uint64_t --> uint32_t
Cортировка ребер каждой вершины
Сортировка всех ребер графа
Большой объем памяти
Слайд 51Резюме: проблемы и подходы к решению задач в рамках одного
узла
Выбор оптимального представления графа
По возможности организация последовательного доступа к данным
По
возможности избегать использовать межпотоковые синхронизации
Стремиться работать не на задержке обращений к памяти, а на темпе
Улучшение локализации
Алгоритмические оптимизации
Сжатие данных
Аккуратная работа с памятью внутри NUMA-вычислительного узла
Балансировка нагрузки
Аккуратно измерять производительность
Слайд 52Проблемы и подходы к решению графовых задач на распределенной памяти
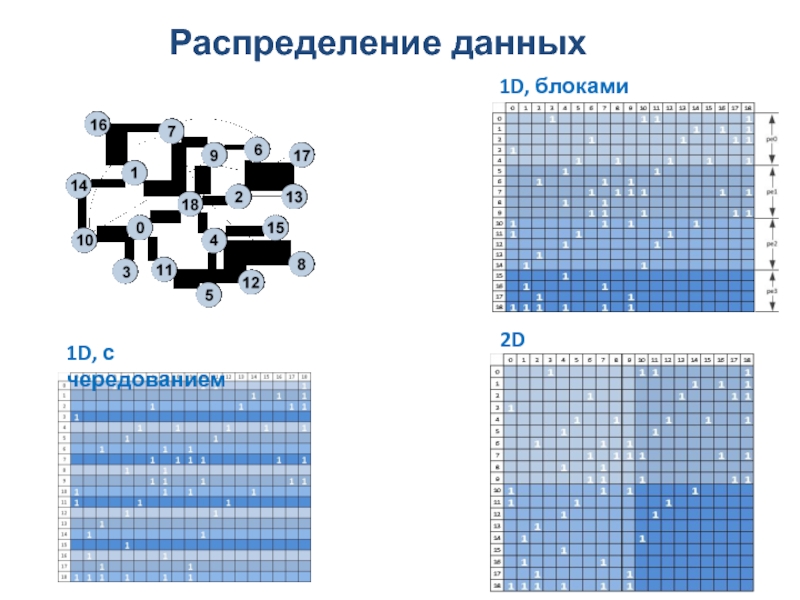
Слайд 54Распределение данных
1D, блоками
1D, с чередованием
2D
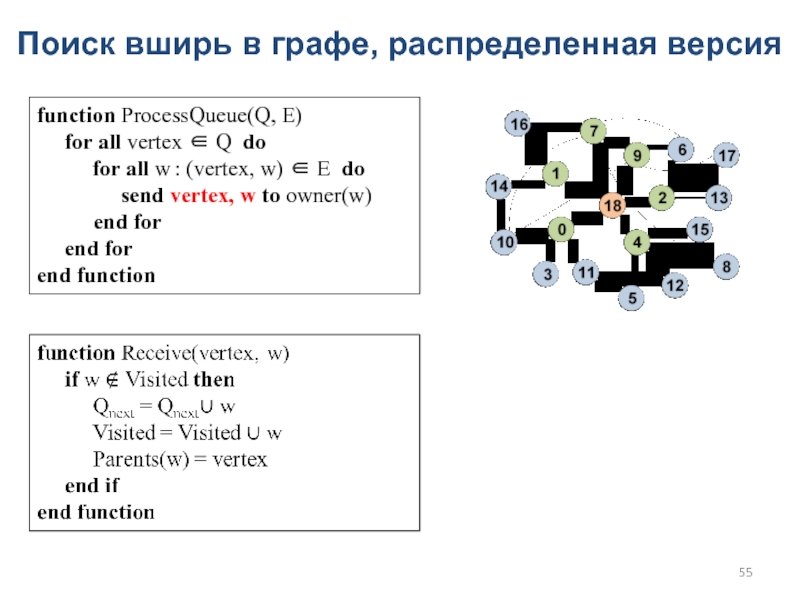
Слайд 55Поиск вширь в графе, распределенная версия
function ProcessQueue(Q, E)
for all vertex ∈ Q do
for all w : (vertex, w) ∈ E do
send vertex, w to owner(w)
end for
end for
end function
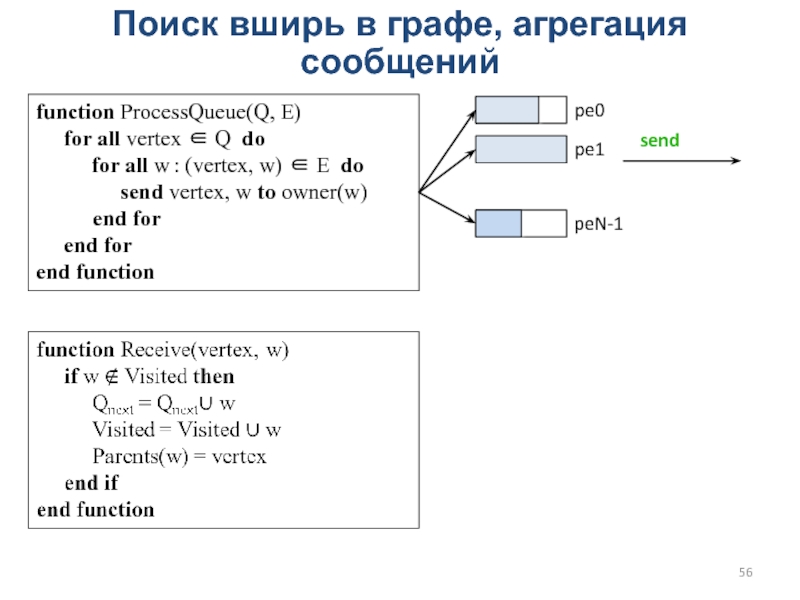
Слайд 56Поиск вширь в графе, агрегация сообщений
function ProcessQueue(Q, E)
for all vertex ∈ Q do
for all w : (vertex, w) ∈ E do
send vertex, w to owner(w)
end for
end for
end function
pe0
pe1
peN-1
send
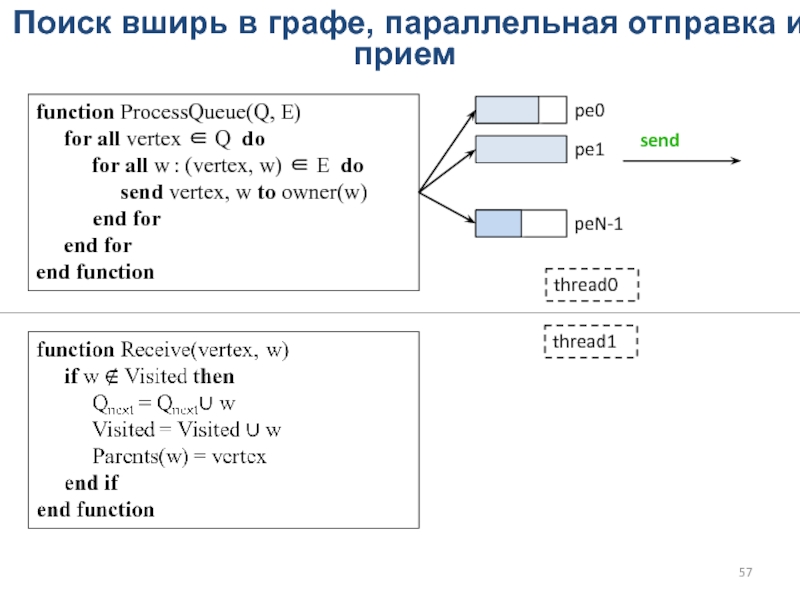
Слайд 57Поиск вширь в графе, параллельная отправка и прием
function ProcessQueue(Q, E)
for all vertex ∈ Q do
for all w : (vertex, w) ∈ E do
send vertex, w to owner(w)
end for
end for
end function
pe0
pe1
peN-1
send
thread0
thread1
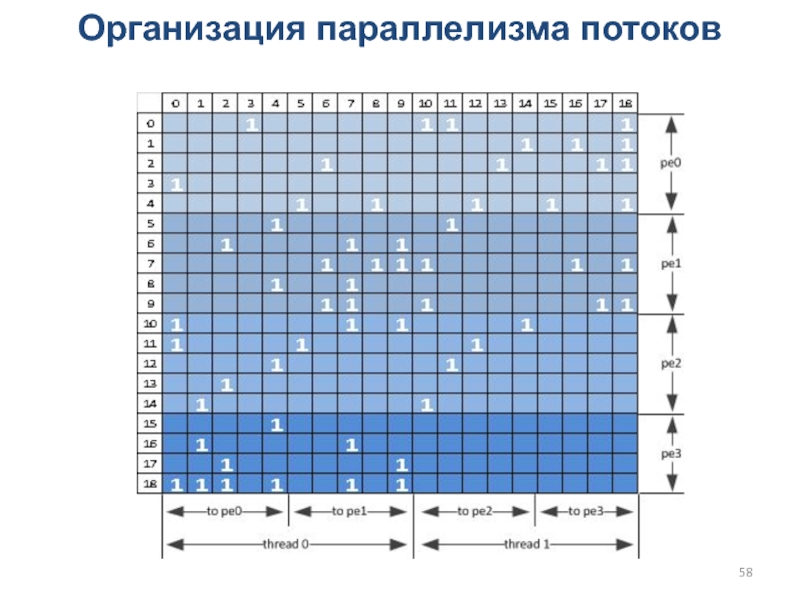
Слайд 58Организация параллелизма потоков
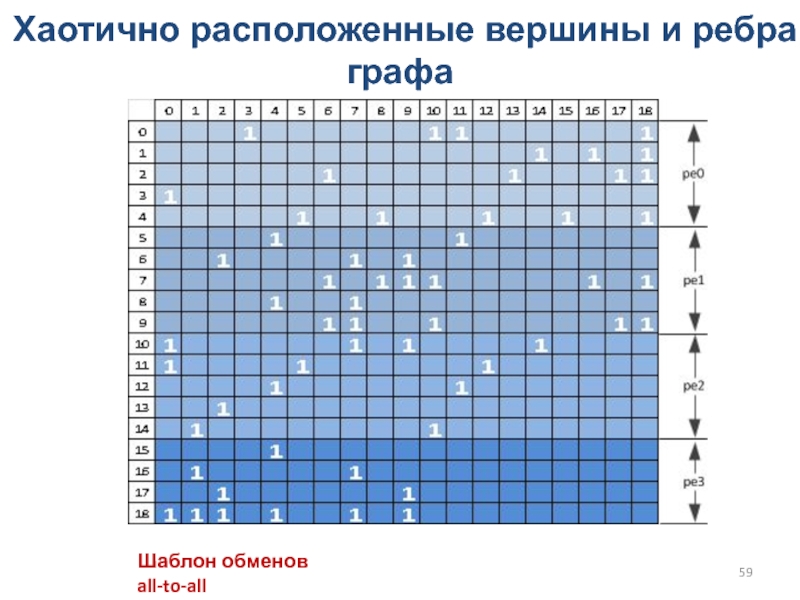
Слайд 59Хаотично расположенные вершины и ребра графа
Шаблон обменов all-to-all
Слайд 60Коммуникационная сеть. Бисекционная пропускная способность
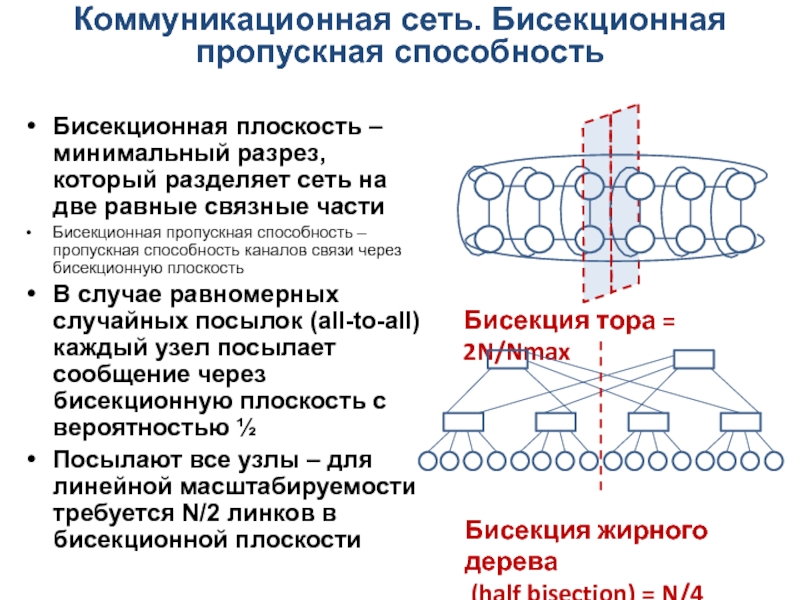
Бисекционная плоскость – минимальный разрез, который
разделяет сеть на две равные связные части
Бисекционная пропускная способность
– пропускная способность каналов связи через бисекционную плоскость
В случае равномерных случайных посылок (all-to-all) каждый узел посылает сообщение через бисекционную плоскость с вероятностью ½
Посылают все узлы – для линейной масштабируемости требуется N/2 линков в бисекционной плоскости
Бисекция тора = 2N/Nmax
Бисекция жирного дерева
(half bisection) = N/4
Слайд 61 nPE
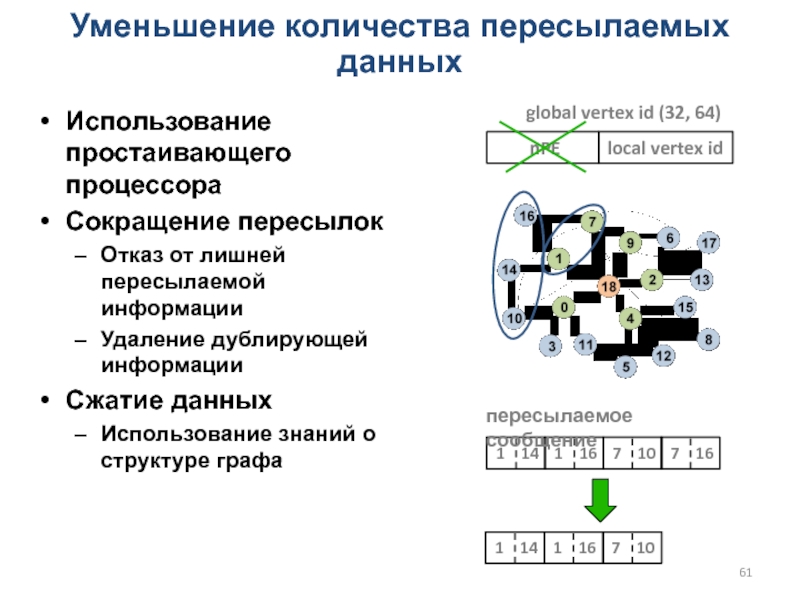
Уменьшение количества пересылаемых данных
Использование простаивающего процессора
Сокращение пересылок
Отказ от лишней
пересылаемой информации
Удаление дублирующей информации
Сжатие данных
Использование знаний о структуре графа
local vertex
id
global vertex id (32, 64)
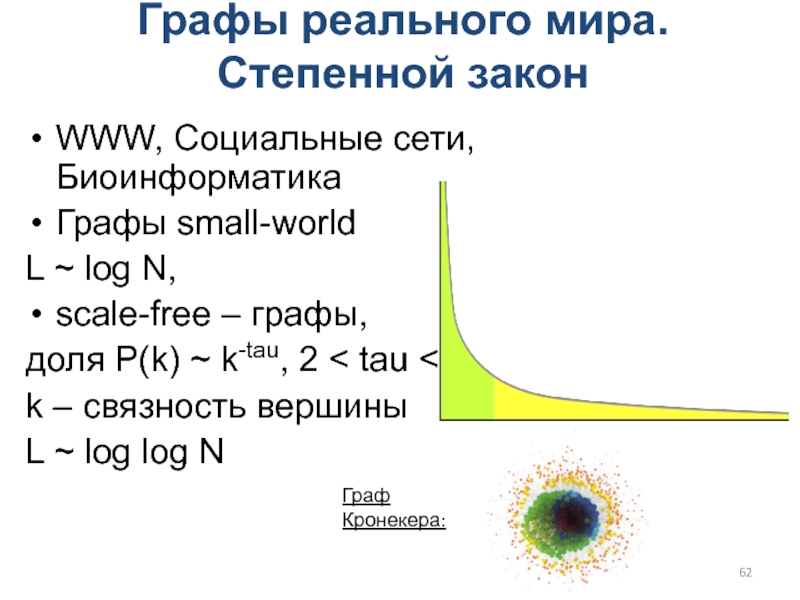
Слайд 62Графы реального мира. Степенной закон
WWW, Социальные сети, Биоинформатика
Графы small-world
L ~
log N,
scale-free – графы,
доля P(k) ~ k-tau, 2 < tau
< 3
k – связность вершины
L ~ log log N
Граф Кронекера:
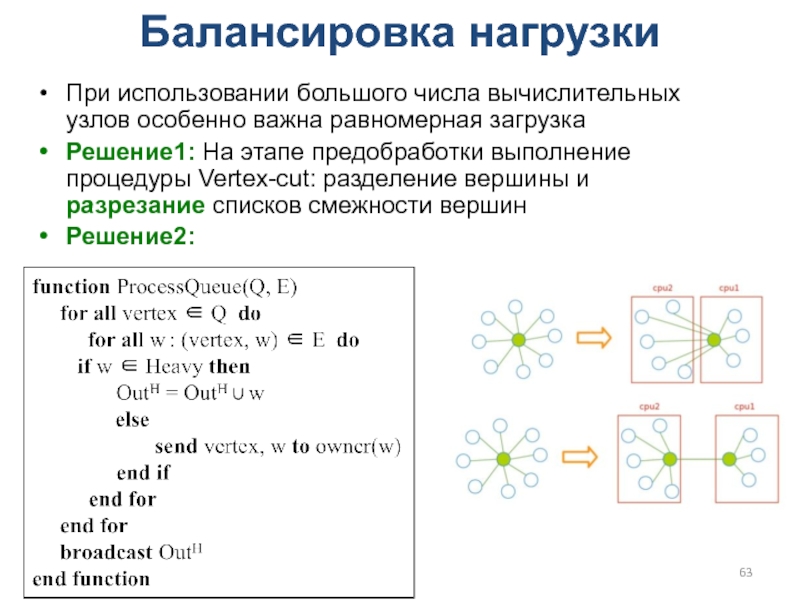
Слайд 63Балансировка нагрузки
При использовании большого числа вычислительных узлов особенно важна равномерная
загрузка
Решение1: На этапе предобработки выполнение процедуры Vertex-cut: разделение вершины и
разрезание списков смежности вершин
Решение2:
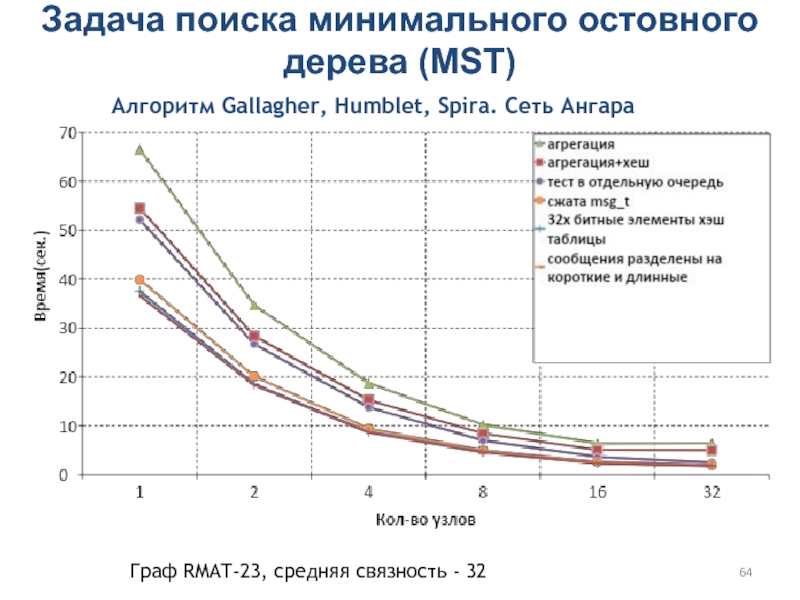
Слайд 64Задача поиска минимального остовного дерева (MST)
Алгоритм Gallagher, Humblet, Spira. Сеть
Ангара
Граф RMAT-23, средняя связность - 32
Слайд 65Проблемы и подходы к решению задач на
распределенной памяти
Выбор распределения данных
Агрегация
сообщений
Организация внутриузлового параллелизма
Уменьшение количества пересылаемых данных
Балансировка нагрузки
Использование эффективных коммуникаций
Аккуратно использовать
MPI
Алгоритмические оптимизации







![Параллельная обработка больших графов Виды графов. LFR*-графПараметры: mu ∈ [0;1], показывает количество связей вне сообщества Виды графов. LFR*-графПараметры: mu ∈ [0;1], показывает количество связей вне сообщества com_tau – показатель степени в законе](/img/thumbs/efab859449e05d7d731ef759042ef228-800x.jpg)





![Параллельная обработка больших графов Поиск вширь в графе (BFS) Подход Queue-based, алгоритм simpleQcounter = 1 Поиск вширь в графе (BFS) Подход Queue-based, алгоритм simpleQcounter = 1 Q[0] = root Visited[root] = 1](/img/thumbs/b8600f44deba9e90c92486ebe9f66237-800x.jpg)