Параллельность плоскостей

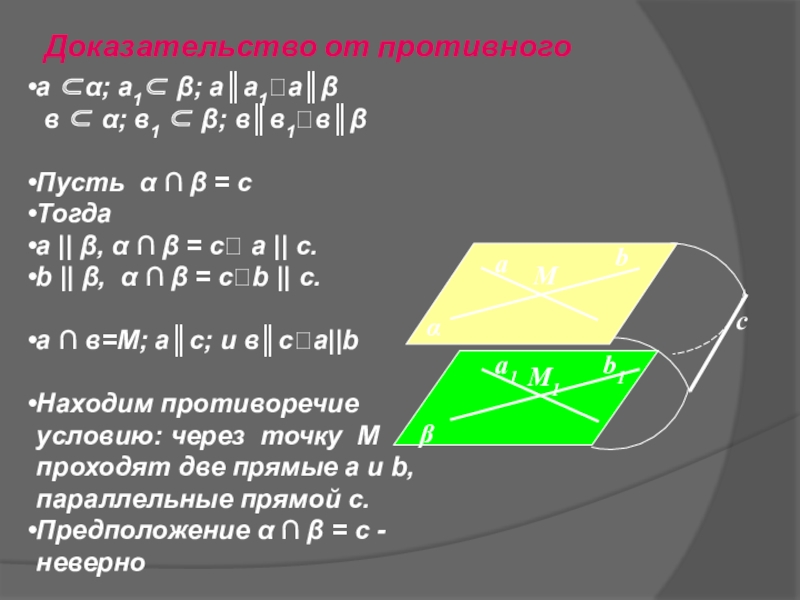
|| a1;
b⊂α, b1⊂ β; b || b1;
a ⋂ b

= M.

Доказать: α || β

М

с

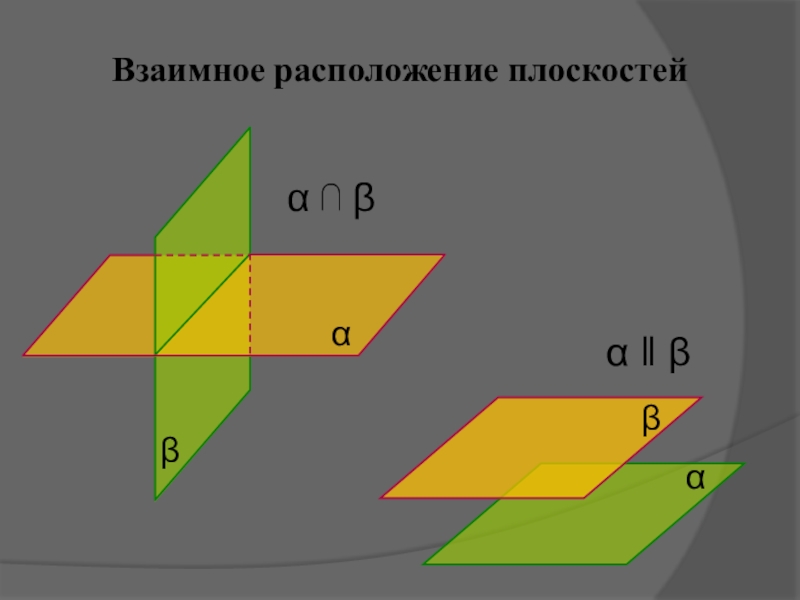
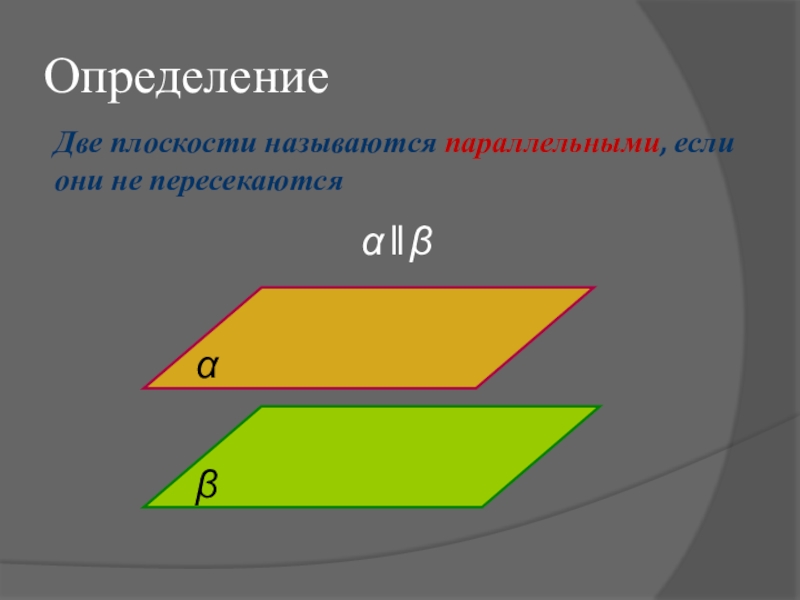
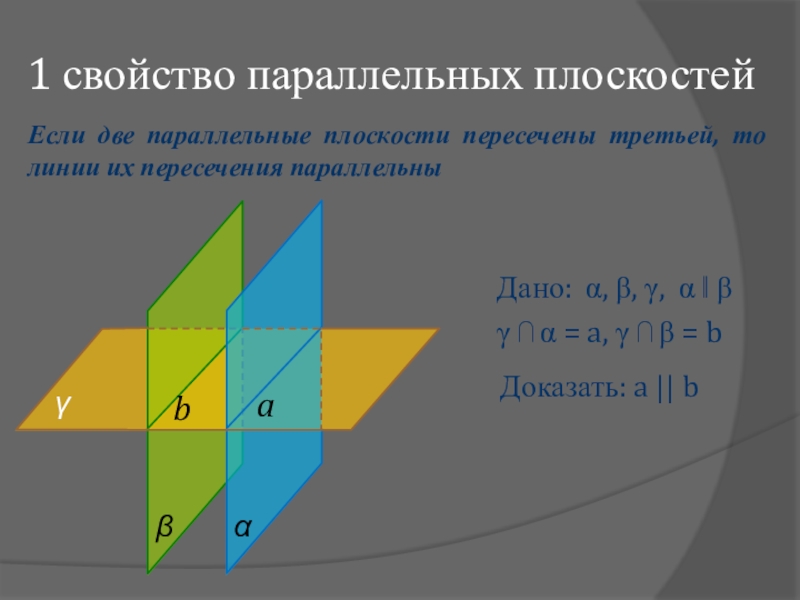
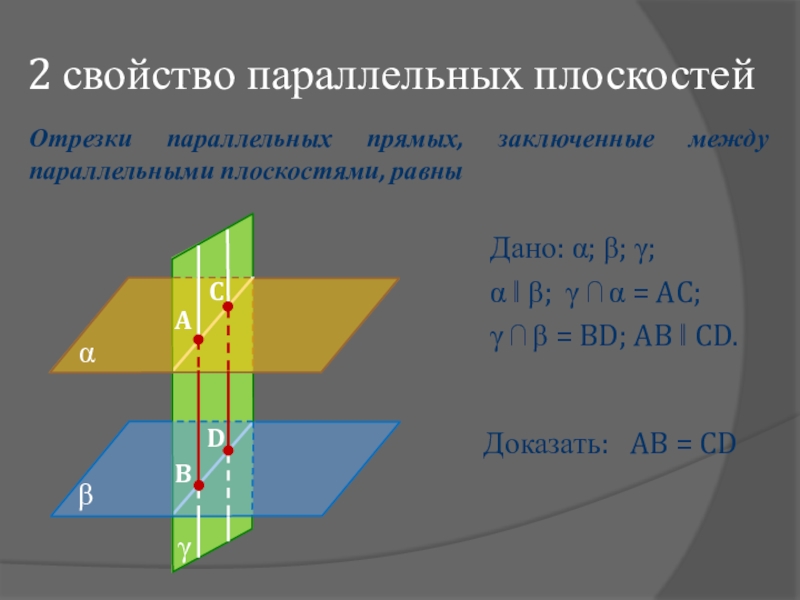
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны

α; в1  β; в║в1в║β

Пусть α ∩ β = с
Тогда

а || β, α ∩ β = с а || с.
b || β, α ∩ β = сb || с.

а ∩ в=М; а║с; и в║са||b

Находим противоречие условию: через точку М проходят две прямые а и b, параллельные прямой с.
Предположение α ∩ β = с - неверно

a, γ ⋂ β = b
Доказать: a || b
Если две

параллельные плоскости пересечены третьей, то линии их пересечения параллельны

1 свойство параллельных плоскостей

AC;
γ ⋂ β = BD; AB ‖ CD.
Доказать:

AB = CD

Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны

2 свойство параллельных плоскостей

(MNP) ‖ (ADC)
б) Найти: S∆MNP

точек?
Верно ли, что если две прямые не пересекаются, то они

параллельны?
Плоскости  и β параллельны, прямая m не лежит в плоскости . Верно ли, что прямая m параллельна плоскости β?
Верно ли, что если прямая а параллельна одной из двух параллельных плоскостей, с другой плоскостью прямая а имеет одну общую точку?
Боковые стороны трапеции параллельны плоскости . Верно ли, что плоскость трапеции параллельна плоскости ?
Две стороны трапеции лежат в параллельных плоскостях. Могут ли эти стороны быть боковыми сторонами трапеции?
Верно ли, что плоскости параллельны, если прямая, лежащая в одной плоскости, параллельна другой плоскости?
Верно ли, что линия пересечения двух плоскостей параллельна одной из этих плоскостей?
Верно ли, что любые четыре точки лежат в одной плоскости?
Верно ли, что если две стороны треугольника параллельны плоскости , то и третья сторона параллельна плоскости ?

A1; AB ⋂ β = A2;
AC ⋂ α = B1;

AC ⋂ β = B2;

Найти:
а) AA2 и AB2;
б) A2B2 и AA2.

а) A1A2=2A1A; A1A2=12см; AB1=5см;
б) A1B1=18см; AA1=24см; AA2=1,5A1A2.