Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Передаточные функции линейных САУ
Содержание
- 1. Передаточные функции линейных САУ
- 2. Передаточная функция разомкнутой системы по возмущающему воздействиюПередаточная функция разомкнутой цепиПередаточная функция замкнутой системы по задающему воздействию
- 3. Иначе
- 4. УСТОЙЧИВОСТЬ САУПонятие устойчивости линейных непрерывных САУ Система
- 5. где
- 6. Если
- 7. Мнимая ось плоскости корней служит границей устойчивостиПараметры,
- 8. Критерии устойчивости САУПравила, позволяющие определять устойчивость системы
- 9. Критерий устойчивости Гурвица Пусть задан характеристический полином САУОпределитель Гурвица (составлен по следующим правилам):
- 10. в диагональ определителя вносятся коэффициенты, начиная с
- 11. Таким образомСАУ устойчива при САУ неустойчива приСАУ находится на границе устойчивости приЧастные случаи систем
- 12. 1. Определитель Гурвица
- 13. Вывод – с повышением порядка систем вероятность
- 14. Система устойчива, если годограф Михайлова, начинаясь на
- 15. На границе устойчивостиРасчетные выражения для граничных параметров,
- 16. Критерий устойчивости Найквиста Позволяет оценить устойчивость замкнутой
- 17. Для устойчивости замкнутой САУ необходимо и достаточно,
- 18. Физический смысл критерия Найквиста заключается в том,
- 19. Оценка устойчивости САУ по логарифмическим частотным характеристикам.
- 20. Слайд 20
- 21. В ряде случаев АФЧХ дважды пересекает отрицательную
- 22. Система будет устойчивой, если все частоты переворота
- 23. Запасы устойчивостиЗапас устойчивости по амплитуде (модулю) определяется
- 24. Слайд 24
- 25. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Передаточные функции линейных САУ
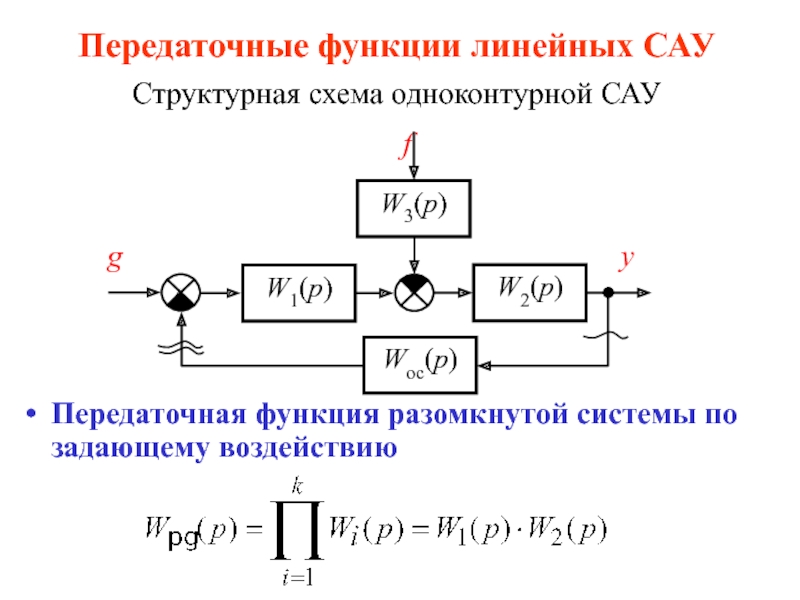
Структурная схема одноконтурной САУ
Передаточная функция разомкнутой системы
по задающему воздействию
Слайд 2Передаточная функция разомкнутой системы по возмущающему воздействию
Передаточная функция разомкнутой цепи
Передаточная
функция замкнутой системы по задающему воздействию
Слайд 3
Иначе
,
где характеристический полином
САУполином числителя этой передаточной функции
Передаточная функция замкнутой системы по возмущающему воздействию
Слайд 4УСТОЙЧИВОСТЬ САУ
Понятие устойчивости линейных непрерывных САУ
Система называется устойчивой, если:
после снятия воздействия по окончании переходного процесса система возвращается в
исходное равновесное состояние после изменения воздействия на постоянную величину по окончании переходного процесса система приходит в новое равновесное состояние
Пусть передаточная функция
замкнутой по какому-либо из воздействий САУ имеет только n простых полюсов, т.е. корней характеристического уравнения
тогда при подаче на её вход единичного ступенчатого воздействия переходная функция будет иметь вид
Слайд 5
где
– установившаяся
(вынужденная) составляющая, однозначно связанная с изменением входной величины – свободная
составляющая, изменяющаяся во времени в течение переходного процесса
Пусть полюсы ПФ – комплексные, т.е.
Слайд 6Если , то свободная
составляющая будет затухать
Если
, то будут иметь место расходящиеся колебанияТаким образом, общим условием затухания всех составляющих является отрицательность вещественных частей всех полюсов передаточной функции САУ. Если хотя бы один полюс имеет положительную вещественную часть, переходный процесс будет расходящимся и система будет неустойчивой
Иначе, необходимым и достаточным условием устойчивости САУ является расположение всех полюсов ее передаточной функции в левой комплексной полуплоскости
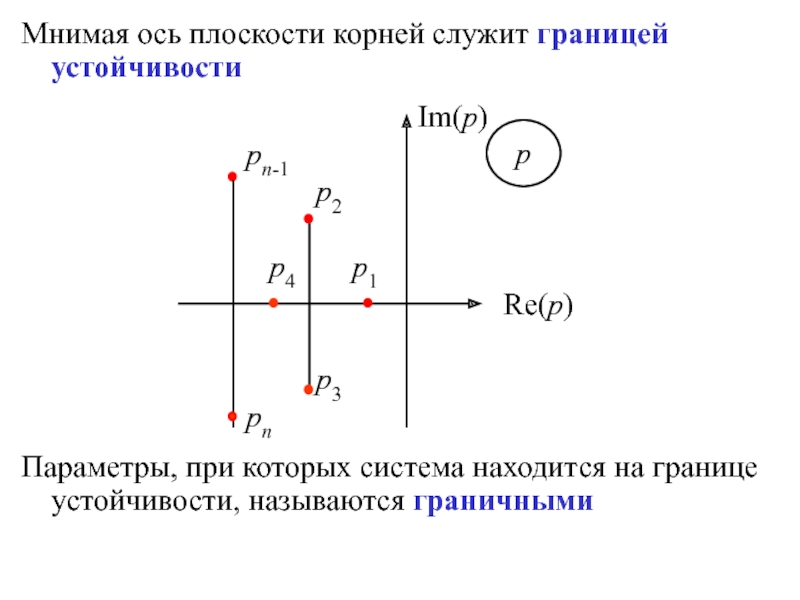
Слайд 7Мнимая ось плоскости корней служит границей устойчивости
Параметры, при которых система
находится на границе устойчивости, называются граничными
Im(p)pn-1
p2
p4 p1
Re(p)
p3
pn
p
Слайд 8Критерии устойчивости САУ
Правила, позволяющие определять устойчивость системы без вычисления корней,
называются критериями устойчивости
Различают алгебраические и частотные критерии устойчивости
К алгебраическим
критериям относятсяКритерий Гурвица
Критерий Рауса
Критерий Рауса-Гурвица
К частотным критериям относятся
Критерий Михайлова
Критерий Найквиста
Слайд 9Критерий устойчивости Гурвица
Пусть задан характеристический полином САУ
Определитель Гурвица
(составлен
по следующим правилам):
Слайд 10в диагональ определителя вносятся коэффициенты, начиная с
и заканчивая ;
в
столбцы вписываются остальные коэффициенты, причем вверх от диагонали индекс коэффициентов уменьшается на единицу, а вниз – уменьшается на единицу; оставшиеся свободные места в столбцах заполняются нулями
Система будет устойчива, если определитель Гурвица
будет положителен
Если , то
где главный минор определителя Гурвица
Слайд 11
Таким образом
САУ устойчива при
САУ неустойчива при
САУ находится на границе
устойчивости при
Частные случаи систем
Слайд 121.
Определитель Гурвица
и система всегда устойчива
2.
Определитель Гурвица
и система также всегда устойчива
3.
Главный минор определителя Гурвица
система может быть
устойчивой или
неустойчивой
Слайд 13Вывод – с повышением порядка систем вероятность их неустойчивости возрастает
Критерий
устойчивости Михайлова
Пусть задан характеристический полином САУ
Заменим в нём оператор
Лапласа р на переменную тогда получим
Кривая, которую описывает радиус- вектор функции
на комплексной плоскости при изменении
частоты от нуля до бесконечности, называется
годографом Михайлова
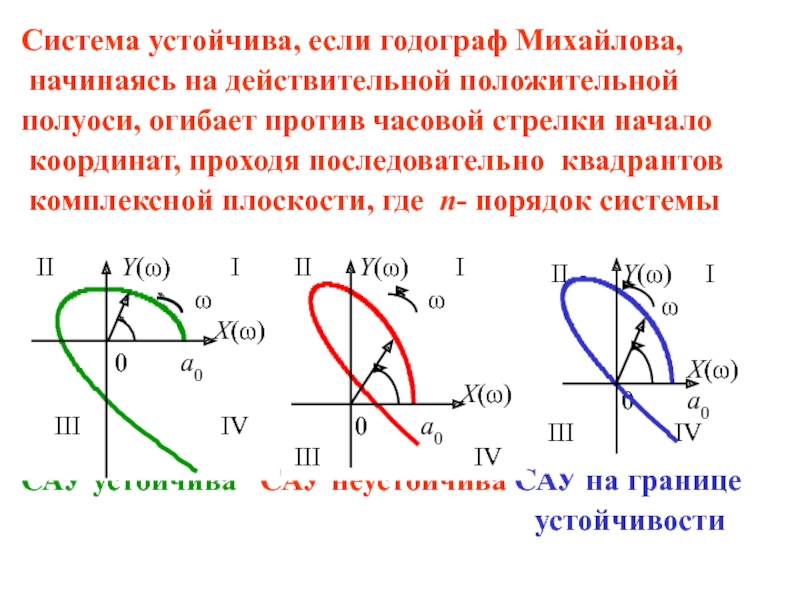
Слайд 14Система устойчива, если годограф Михайлова,
начинаясь на действительной положительной
полуоси,
огибает против часовой стрелки начало
координат, проходя последовательно квадрантов
комплексной
плоскости, где n- порядок системыСАУ устойчива САУ неустойчива САУ на границе
устойчивости
Слайд 15На границе устойчивости
Расчетные выражения для граничных параметров, полученные по критериям
Гурвица и Михайлова, совпадают.
Физический смысл величины
– это частота собственных колебаний системы на границе устойчивости
Слайд 16Критерий устойчивости Найквиста
Позволяет оценить устойчивость замкнутой САУ по ее
разомкнутой цепи
В передаточной функции
производят замену оператора р на переменную jω и на комплексной плоскости при изменении частоты от нуля до бесконечности строят АФЧХ (годограф Найквиста)Если разомкнутая цепь устойчива (а это всегда имеет место, если САУ не содержит неустойчивых неминимально фазовых звеньев), то формулировка критерия Найквиста звучит следующим образом
Слайд 17Для устойчивости замкнутой САУ необходимо и достаточно, чтобы годограф Найквиста
при изменении ω от нуля до бесконечности не охватывал точку
с координатами (-1, j0)САУ устойчива САУ неустойчива САУ на
границе устойчивости
ImW(jω)
ReW(jω)
-1 0 ω = 0
ω
Слайд 18Физический смысл критерия Найквиста заключается в том, что при увеличении
частоты входного воздействия сигнал, проходящий по цепи обратной связи, оказывается
в противофазе с входным. Это равносильно замене отрицательной обратной связи на положительную. Если же при этой частоте разомкнутый контур обладает усилением (т.е. ), то замкнутая САУ становится неустойчивойНа границе устойчивости
Частота ωπ, соответствует повороту радиус-вектора АФЧХ разомкнутой цепи на угол -π и называется частотой переворота фазы или частотой Найквиста
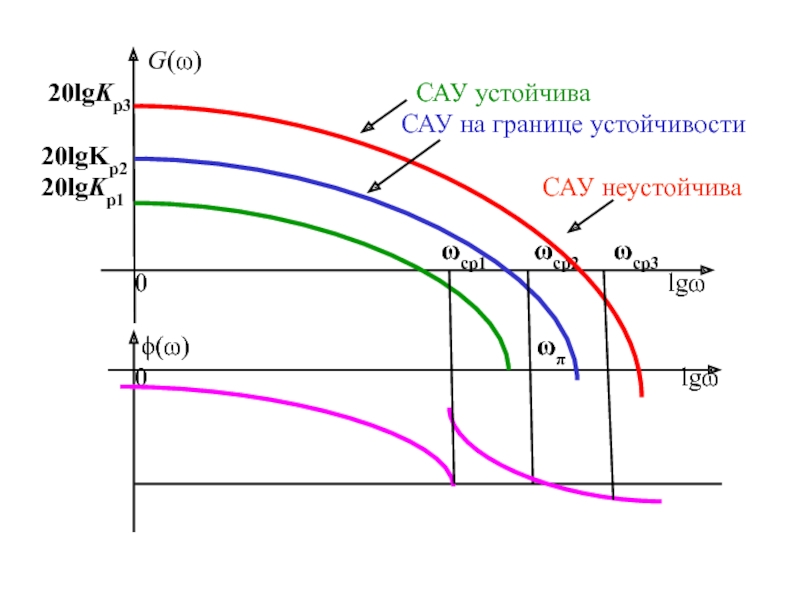
Слайд 19Оценка устойчивости САУ по логарифмическим частотным характеристикам. Запасы устойчивости
Если
годограф АФЧХ не охватывает точку с координатами (-1, j0) то
при частоте, на которой, абсолютное значение фазы меньше -π. Но значение соответствует
Поэтому для устойчивости замкнутой САУ необходимо, чтобы ЛАЧХ разомкнутой цепи пересекла ось абсцисс раньше, чем фаза, спадая, окончательно перейдет за значение -π.
Однако ЛАЧХ равна нулю на частоте среза , а
на частоте переворота фазы . Следовательно, система будет абсолютно устойчива, если
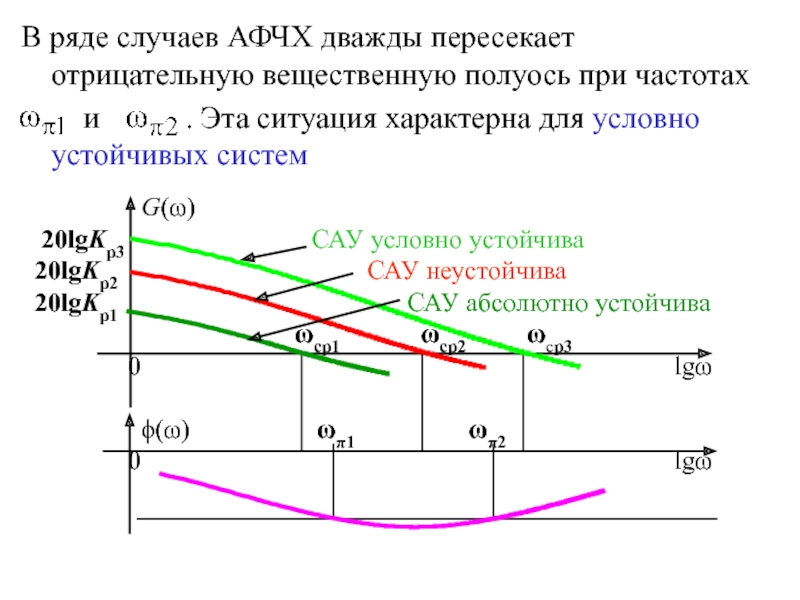
Слайд 21В ряде случаев АФЧХ дважды пересекает отрицательную вещественную полуось при
частотах
и
. Эта ситуация характерна для условно устойчивых систем
Слайд 22Система будет устойчивой, если все частоты
переворота фазы больше частоты
среза или если ее
ЛФЧХ до частоты среза принимает значение
четное число раз
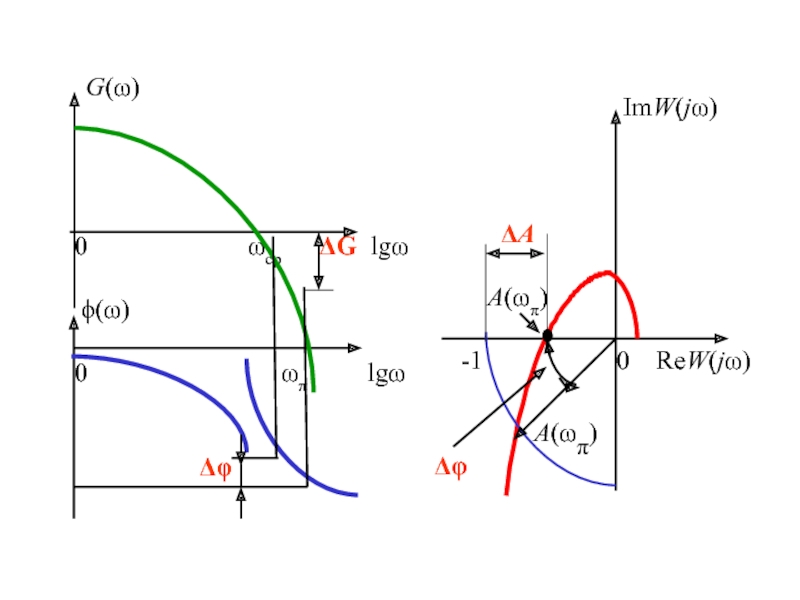
Слайд 23Запасы устойчивости
Запас устойчивости по амплитуде (модулю) определяется величиной
допустимого подъема ЛАЧХ, при котором система окажется на границе
устойчивости:Запас устойчивости по фазе определяется величиной, на которую должно возрасти запаздывание по фазе в системе с частотой среза
, чтобы система оказалась на границе устойчивости. Обычно рассчитывается в градусах