Перемещения деформируемых систем. Лекция 1

типа, места и
направления
перемещения
( по схеме )
Символ причины,
вызвавшей перемещение
( индекс

состояния системы с соответствующим
воздействием )

Δ1k

Δ2k

Δ3k

Δik

Δnk

k

( индекс
состояния
системы )

Читается: перемещение такой-то точки ( сечения )
по такому-то направлению от k–го воздействия.

Если i = k, то Δkk – собственное перемещение
( перемещение, вызванное силовым
воздействием Fk , по его направлению )

A

A1

Fk

k

Направление Fk

Δkk

типа, места и
направления
перемещения
( по схеме )
Символ причины,
вызвавшей перемещение
( индекс

состояния системы с соответствующим
воздействием )

Δ1k

Δ2k

Δ3k

Δik

Δnk

k

( индекс
состояния
системы )

Конкретизация индекса состояния системы
по виду воздействия:

k

F

c

t

силовое воздействие ( нагрузки )

кинематическое воздействие
( смещения связей )

температурное ( тепловое ) воздействие – изменение
температуры

ΔiF

Δic

Δit

ΔiΣ

– от комбинаций
воздействий
F, c, t

А

А1

F

i

i – направление искомого перемещения

ΔiF

А

А1

i

c

Δic

Δto

t

А

А1

i

Δit

)
Символ причины,
вызвавшей перемещение
( индекс состояния системы с соответствующим
единичным воздействием )

k

( индекс состояния
системы )

А

А1

i

i – направление искомого перемещения

B1

Перемещения ( линейные, угловые ), возникающие от равных единице механических воздействий ( силовых или кинематических ),
называются единичными перемещениями.

От единичного
силового
воздействия

От единичного
кинематического
воздействия

Fk = 1

k

( индекс
состояния
системы )

А

А1

i

uB,k = 1

B

Групповое перемещение

Пример: относительное ( взаимное ) линейное перемещение
точек А и В по направлению линии АВ.

А

B

i

F

B1

А1

единичных нагрузок )
J.C. Maxwell ( 1864 ), O. Mohr (

1874 )

ИДЕЯ МЕТОДА МАКСВЕЛЛА – МОРА ( ММ-М )

В дополнение к действительному состоянию
рассчитываемой системы ( при заданных воздействиях )
рассматривается вспомогательное ( фиктивное ) состояние
с единичным силовым воздействием
по направлению искомого перемещения;
силовые факторы вспомогательного единичного состояния затем используются, вместе с соответствующими характеристиками действительного состояния,
для вычисления искомого перемещения.

единичных нагрузок )
Правило задания
вспомогательного единичного воздействия
Во вспомогательном (

фиктивном ) состоянии системы,
рассматриваемом независимо ( отдельно )
от действительного состояния,
в месте, где определяется искомое перемещение,
по его направлению прикладывается численно равное
единице силовое воздействие, тип которого
( сила, момент либо группа сил и/или моментов )
соответствует типу определяемого перемещения
( линейное или угловое, одиночное либо обобщённое ).

В общем случае вспомогательное ( фиктивное )
единичное воздействие – обобщённое, соответствующее
определяемому обобщённому ( групповому ) перемещению.

Кинематическое свойство вспомогательного единичного воздействия:
оно (воздействие) таково, что способно совершить работу
на определяемом перемещении.

единичных нагрузок )
Типовые случаи вспомогательных единичных состояний
а) при определении

одиночных перемещений

Линейное перемещение точки ( A )

Угол поворота сечения ( 1 )
или узла

F

F

Δt o

А

i

Σ

A1

ΔiΣ= ?

А

i

i

Fi = 1

F

q

Σ

1

1’

ΔiΣ= ?

1

i

Mi = 1

б) при определении групповых перемещений

Относительное ( взаимное )
линейное перемещение точек ( A и В )

А

B

i

B1

А1

i

А

B

Fi = 1

Fi = 1

i

F

Относительный ( взаимный )
угол поворота сечений ( 1 и 2 )

i

F

ΔiF= ?

q

1

1’

2’

2

1

2

Mi = 1

единичных нагрузок )
Базовая формула ММ – М
в общем случае

деформируемой системы

В случае линейно деформируемой системы (ЛДС) перемещения действительного состояния могут
быть приняты в качестве виртуальных, т.е. k = Σ

F

q

Δt o

A

A1

Δ( j )

ΔiΣ= ?

i

Действительное состояние системы

A

i

Вспомогательное ( фиктивное )
единичное состояние

Fi = 1

Σ

i

F
t
c

Состояние « i » – равновесное,
его внутренние и внешние силы
удовлетворяют принципу Лагранжа:

Wext, ik + Wint, ik = 0,
i – символ состояния, внешние и внутренние силы
которого совершают возможную работу;
k – индекс виртуальных перемещений.

Wext, iΣ + Wint, iΣ = 0,

R( j ),i

Σ – индекс виртуальных перемещений.

При одновременных смещениях связей
Δ( 1 ) , Δ( 2 ) ,…, Δ( j ) ,…, Δ( r ) :

Из уравнения возможных работ,
с учётом того, что Fi = 1:

базовая формула ММ – М

( Δto )

( Δ(j) )

ЭНЕРГИЯ ДЕФОРМАЦИИ
Возможной работой внешних ( внутренних ) сил называется

работа, совершаемая этими силами
на перемещениях ( деформациях ), вызванных
другими воздействиями ( реальными или виртуальными ).

Действительной работой внешних ( внутренних ) сил называется работа, совершаемая ими на перемещениях
( деформациях ), вызванных самими этими силами.

Потенциальная энергия деформации – это энергия, накапливаемая в материале системы в процессе
его деформирования заданными воздействиями
и возвращаемая в виде механической работы
при разгрузке системы ( материала ).

ЭНЕРГИЯ ДЕФОРМАЦИИ









A

Fi

i


i

k











A

Fk

B

A1

B1




Δik
Δkk

Δkk – собственное перемещение
Δik – побочное перемещение

Возможные работы внешних
и внутренних сил i –го состояния
на перемещениях k –го состояния:
Wext, ik = – Wint, ik

Δik

Fi

Fi

Δik

Δik = inv ( Fi )

Wext, ik = – Wint, ik = Fi* Δik

Fk

Fk

Δkk

Δkk

ζ

Fk(ζ)

dζ

Действительная работа
внешних сил
k –го состояния:

0

0

0 < η < 1

ЭНЕРГИЯ ДЕФОРМАЦИИ









A

Fi

i

i

k









A

Fk

B

A1

B1



Δik
Δkk

Δkk – собственное перемещение
Δik – побочное перемещение

Δik

Fi

Fi

Δik

Действительная работа
внешних сил
k –го состояния:

0

η = 1/2

Wext, ik = – Wint, ik = Fi* Δik

Fk

Fk

Δkk

Δkk

ζ

Fk(ζ)

dζ

0

Для ЛДС

Fk

Fk

Δkk

Δkk

ζ

Fk(ζ)

dζ

0

Теорема Клапейрона
( B.P.E. Clapeyron, 1834 )

U – ПЭУД

Возможные работы внешних
и внутренних сил i –го состояния
на перемещениях k –го состояния:
Wext, ik = – Wint, ik

Δik = inv ( Fi )

ЭНЕРГИЯ ДЕФОРМАЦИИ









A

Fi

i

i

k









A

Fk

B

A1

B1



Δik
Δkk

Возможные работы внешних
и внутренних сил i –го

состояния
на перемещениях k –го состояния:

Действительная работа внешних
и внутренних сил k –го состояния,
потенциальная энергия упругой
деформации (ПЭУД) ЛДС:

Wext, ik = – Wint, ik = Fi* Δik

Теорема Клапейрона

Выражения возможных и действительных
работ внешних и внутренних сил и ПЭУД
через внешние силовые факторы
и перемещения
( через обобщённые нагрузки
и обобщённые перемещения ).

ЭНЕРГИЯ ДЕФОРМАЦИИ









A

Fi

i

i

k









A

Fk

B

A1

B1



Δik
Δkk

Выражения возможных и действительных работ внешних и внутренних

сил
и ПЭУД через внутренние силовые факторы ( напряжения ) и деформации

σx,i

σy,i

σz,i

τxy,i

τxz,i

τyz,i

εx,k
εy,k
εz,k
γxy,k
γyz,k
γzx,k

dx

dy

dz

ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных и действительных работ внешних и внутренних

сил
и ПЭУД через внутренние силовые факторы ( напряжения ) и деформации

Физические зависимости, связывающие деформации k –го состояния с напряжениями
( для линейно деформируемого изотропного тела, с учётом температурной составляющей )

ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных работ внешних и внутренних сил через

внутренние силовые факторы в стержневых системах с прямолинейными элементами
и стержнями малой кривизны

F

q

Δt o

В

В1

Δ( j )

ΔiΣ

В

i

Fi = 1

Σ

i

F
t
c

В случае ЛДС ΔiΣ = ΔiF + Δit + Δic

i

ΔiΣ Wint, iΣ = ?

Вспомогательное единичное состояние

ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных работ внешних и внутренних сил через

внутренние силовые факторы в стержневых системах с прямолинейными элементами
и стержнями малой кривизны

F

q

В

В1

i

ds

ΔiF

i

Fi = 1

F

i

ds

Действительное состояние – силовое

В

ΔiF Wint, iF = ?

Qi

Qi ( Qy,i )

Ni

Ni

Mi ( Mz,i )

Mi + dMi

z

y

ds

QF

NF

QF

NF

MF

MF +…

QF +…

NF +…

MF +…

QF +…

NF +…

ds

MF

Вспомогательное единичное состояние

ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных работ внешних и внутренних сил через

внутренние силовые факторы в стержневых системах с прямолинейными элементами
и стержнями малой кривизны

F

q

В

В1

i

ds

ΔiF

i

Fi = 1

F

i

ds

В

ΔiF Wint, iF = ?

Qi

Qi ( Qy,i )

Ni

Ni

Mi ( Mz,i )

Mi + dMi

z

y

ds

QF

NF

MF

QF

NF

ds

MF

dθF

ΔdsF

dvF

ΔdsF

dvF

dθF

γ0,F

QF

QF

NF

NF

MF

MF

~0

ds

dWint, iF = – dWext, iF =
= – (dWM, iF + dWN, iF + dWQ, iF )

Для i-го равновесного
состояния элемента ds
линейно деформируемой системы:

Изгиб

Сдвиг

Растяжение
( сжатие )

Вспомогательное единичное состояние

Действительное состояние – силовое

ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных работ внешних и внутренних сил через

внутренние силовые факторы в стержневых системах с прямолинейными элементами
и стержнями малой кривизны

F

q

В

В1

i

ds

ΔiF

i

Fi = 1

F

i

ds

В

ΔiF Wint, iF = ?

Qi

Qi ( Qy,i )

Ni

Ni

Mi ( Mz,i )

Mi + dMi

z

y

ds

ΔdsF

dvF

dθF

γ0,F

QF

QF

NF

NF

MF

MF

~0

ds

dWint, iF = – dWext, iF =
= – (dWM, iF + dWN, iF + dWQ, iF )

Для i-го равновесного
состояния элемента ds
линейно деформируемой системы:

Изгиб

Сдвиг

Растяжение
( сжатие )

dWM, iF = Mi * dθF = Mi * ρF * ds

dWN, iF = Ni * ΔdsF = Ni * εF * ds

dWQ, iF = Qi * dvF = Qi * γ0,F * ds

По закону Гука при изгибе, растяже-
нии (сжатии) и сдвиге соответственно:

ρF = MF / EI; εF = NF / EA;
γ0,F = τ0,F /G = (kτ* QF /A)/G

kτ – коэффициент неравномерности
распределения касательных
напряжений по сечению

Вспомогательное единичное состояние

Действительное состояние – силовое

ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных работ внешних и внутренних сил через

внутренние силовые факторы в стержневых системах с прямолинейными элементами
и стержнями малой кривизны

F

q

В

В1

i

ds

ΔiF

i

Fi = 1

F

i

ds

В

ΔiF Wint, iF = ?

Qi

Qi ( Qy,i )

Ni

Ni

Mi ( Mz,i )

Mi + dMi

z

y

ds

ΔdsF

dvF

dθF

γ0,F

QF

QF

NF

NF

MF

MF

~0

ds

dWint, iF = – dWext, iF =
= – (dWM, iF + dWN, iF + dWQ, iF )

Для i-го равновесного
состояния элемента ds
линейно деформируемой системы:

Изгиб

Сдвиг

Растяжение
( сжатие )

Вспомогательное единичное состояние

Действительное состояние – силовое

ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных работ внешних и внутренних сил через

внутренние силовые факторы в стержневых системах с прямолинейными элементами
и стержнями малой кривизны

F

q

В

В1

i

ds

ΔiF

i

Fi = 1

F

i

ds

В

ΔiF Wint, iF = ?

Qi

Qi ( Qy,i )

Ni

Ni

Mi ( Mz,i )

Mi + dMi

z

y

ds

ΔdsF

dvF

dθF

γ0,F

QF

QF

NF

NF

MF

MF

~0

ds

dWint, iF = – dWext, iF =
= – (dWM, iF + dWN, iF + dWQ, iF )

Для i-го равновесного
состояния элемента ds
линейно деформируемой системы:

Изгиб

Сдвиг

Растяжение
( сжатие )

Обобщение на случай
пространственного сложного
сопротивления стержня:

Вспомогательное единичное состояние

Действительное состояние – силовое

ЭНЕРГИЯ ДЕФОРМАЦИИ
Выражения возможных работ внешних и внутренних сил через

внутренние силовые факторы в стержневых системах с прямолинейными элементами
и стержнями малой кривизны

F

q

В

В1

i

ds

ΔiF

i

Fi = 1

F

i

ds

В

ΔiF Wint, iF = ?

Обобщение на случай
пространственного сложного
сопротивления стержня:

j

dsj

Элемент ds j – му элементу / участку ( )
системы, имеющей m элементов / участков,
тогда для всей системы:

Вспомогательное
единичное состояние

Действительное состояние – силовое

F
q

В

В1
i


ds



ΔiF






i
Fi = 1

F

i



ds
В



ΔiF Wint, iF =

?

j

dsj

По базовой формуле ММ – М:
ΔiF = – Wint, iF

lj

Вспомогательное
единичное состояние

Действительное состояние – силовое

F
q

В

В1
i


ds



ΔiF






i
Fi = 1

F

i



ds
В





j
dsj
По базовой формуле ММ – М:
ΔiF = –

Wint, iF

lj

В общем случае все величины в подынтегральном выражении – функции
координаты сечения sj ( для прямолинейного стержня – xj ):

Mz,i = Mz,i (sj ), Mz,F = Mz,F (sj ) ,…, NF = NF (sj ), …, Qz,F = Qz,F (sj ) ,
EIz = EIz (sj ) ,…, GIt = GIt (sj ) , EA = EA(sj ) , GA = GA(sj ) ,…, kτz = kτz (sj )

Вариант записи формулы Максвелла – Мора
для перемещения от силовых воздействий:

Вспомогательное
единичное состояние

Действительное состояние – силовое

F
q

В

В1
i


ds



ΔiF






i
Fi = 1

F

i



ds
В





j
dsj
По базовой формуле ММ – М:
ΔiF = –

Wint, iF

lj

Учёт деформируемых ( нежёстких ) упругоподатливых связей в системе:

cθ

cθ

cΔ

Rj

Rj

Закон Гука для
упругих связей:
Rj = cj * Δj

Жёсткости линейных и угловых упругих связей

u – суммарное число
внешних и внутренних
упругих связей

Вспомогательное
единичное состояние

Вариант записи формулы Максвелла – Мора
для перемещения от силовых воздействий:

Действительное состояние – силовое

Изгиб

Изгиб

Кручение

Растяжение/сжатие

Сдвиг

Сдвиг

F
q

В

В1
i


ds



ΔiF






i
Fi = 1

F

i



ds
В





j
dsj
По базовой формуле ММ – М:
ΔiF = –

Wint, iF

lj

Краткая запись формулы Максвелла – Мора
для перемещения от силовых воздействий:

Вспомогательное
единичное состояние

S… – обобщённое обозначение
внутреннего силового
фактора: S…

Mz,…
My,…
Mt,…
N…
Qy,…
Qz,…

CS – обобщённое обозначение
жёсткости сечения при
деформации, соответству-
ющей силовому фактору S:

CS

EIz
EIy
GIt
EA
GA/kτy
GA/kτz

Действительное состояние – силовое

Приложение
К вопросу об учёте деформации сдвига при определении перемещений

y


По

закону Гука
при сдвиге

ds

i

F

Формула выводится путём сопоставления выражений возможных работ
по двум расчётным моделям элемента ds:

1. Формула для коэффициента kτ

а) с фактическими касательными напряжениями
τi (y) в концевых сечениях элемента ds во вспо-
могательном i-ом единичном состоянии и фак-
тическими деформациями сдвига γF (y) в дейст-
вительном состоянии:

б) с обобщёнными силами ( поперечными
силами Qi ) в концевых сечениях эле-
мента ds в i-ом единичном состоянии
и соответствующими обобщёнными
перемещениями ( абсолютным сдвигом
dvF ) в действительном состоянии:

z

y

b( y)

y

ds

i

F

Qi

Qi

dvF = γ0,F * ds

dy

dV

τF ( y)

QF

QF

h

Приложение
К вопросу об учёте деформации сдвига при определении перемещений

y


По

закону Гука
при сдвиге

ds

i

F

Формула выводится путем сопоставления выражений возможных работ
по двум расчётным моделям элемента ds:

1. Формула для коэффициента kτ

а) с фактическими касательными напряжениями
τi (y) в концевых сечениях элемента ds во вспо-
могательном i-ом единичном состоянии и фак-
тическими деформациями сдвига γF (y) в дейст-
вительном состоянии: ё

б) с обобщёнными силами ( поперечными
силами Qi ) в концевых сечениях эле-
мента ds в i-ом единичном состоянии
и соответствующими обобщёнными
перемещениями ( абсолютным сдвигом
dvF ) в действительном состоянии:

z

y

b( y)

y

ds

i

F

Qi

Qi

dvF = γ0,F * ds

dy

τF ( y)

QF

QF

h

Значения коэффициента kτ для некоторых видов сечений:

kτ = 6/5

kτ = 10/9

kτ A/Aw

Приложение
К вопросу об учёте деформации сдвига при определении перемещений
Составляющая

перемещения ΔiF , обусловленная деформацией сдвига, – ΔiF,Q ;
в отношении к составляющей ΔiF,M от изгиба: ΔiF,Q /ΔiF,M = αQ

2. Оценка влияния сдвига на перемещения от силовых воздействий

Признаки необходимости учёта деформации сдвига
при определении перемещений стержневых систем:
сечение – тонкостенное ( kτ > 2 );
материал – относительно низкомодульный при сдвиге ( E/G > 3…4 );
элемент достаточно массивный, «короткий» ( h/l > 1/8 );
нагрузки таковы, что вызывают значительные поперечные силы
при сравнительно небольших изгибающих моментах
( ориентировочно: средние на грузовом участке | M/Q | < ~ h ).

Подробнее см.: Себешев В.Г. Особенности работы статически неопределимых систем
и регулирование усилий в конструкциях: учебное пособие. –
Новосибирск: НГАСУ (Сибстрин), 2009. – 164 с.

Для j-го участка / элемента постоянного сечения:

где < 0,5 – относительный радиус инерции сечения;

е в о п р о с ы
( в

скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 29» )
1. Как в общем виде обозначаются перемещения? Какой смысл имеют индексы в этом обозначении? ( 2 )
2. Что такое собственное перемещение? ( 2 )
3. Какие индексы используются для обозначения перемещений от силовых, температурных, кинематических и комбинированных воздействий? ( 3 )
4. Какие перемещения называются единичными? ( 4 )
4. Какова основная идея метода Максвелла – Мора определения перемещений деформируемых систем? Почему этот метод также называется методом единичных вспомогательных нагрузок? ( 5 )
5. Правило задания вспомогательного единичного воздействия. Каков кинематический смысл этого воздействия? ( 6 )
6. Типовые случаи вспомогательных единичных состояний в методе Максвелла – Мора.
( 7 )
7. Какой принцип механики лежит в основе метода Максвелла – Мора? ( 8 )
8. Через какие величины выражается искомое перемещение по базовой формуле метода Максвелла – Мора? ( 8 )
9. Что такое возможная работа внешних или внутренних сил? ( 9 )
10. Какая работа внешних или внутренних сил называется действительной? ( 9 )
11. Что называется потенциальной энергией деформации системы? ( 9 )
12. Как связаны возможные работы внешних и внутренних сил ( 10 ) 12. Как связаны возможные работы внешних и внутренних сил ( 10 ) , их действительные работы и потенциальная энергия упругой деформации (ПЭУД)? ( 12 )
_____________________________________________________
*) Только в режиме «Показ слайдов»

е в о п р о с ы
( в

скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 30» )
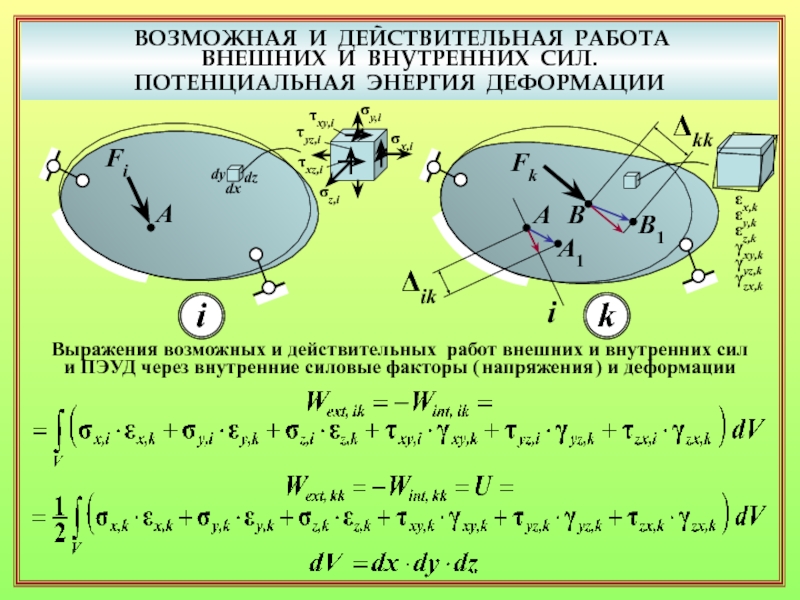
13. Как выражаются возможные и действительные работы внешних и внутренних сил
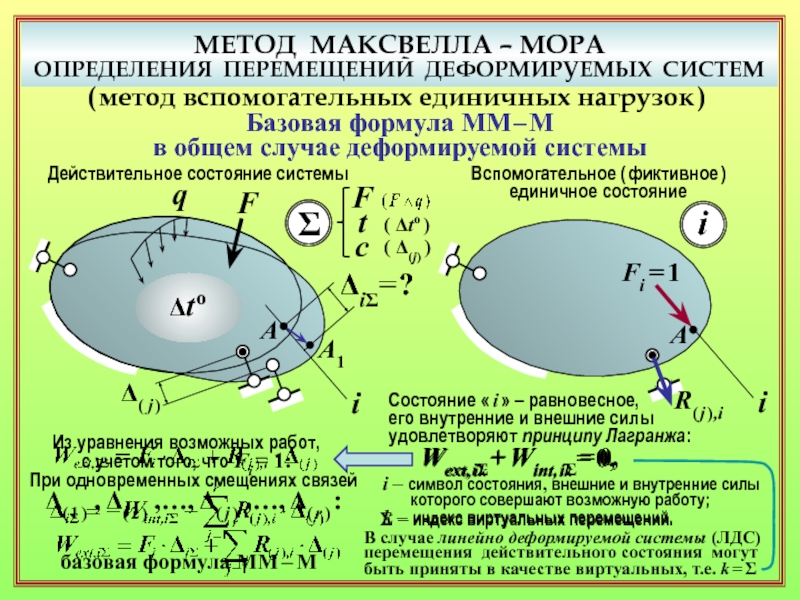
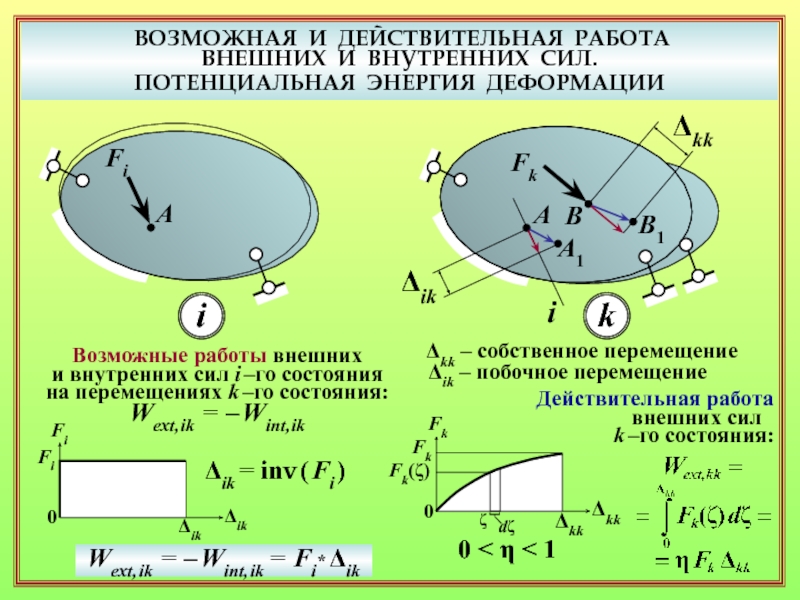
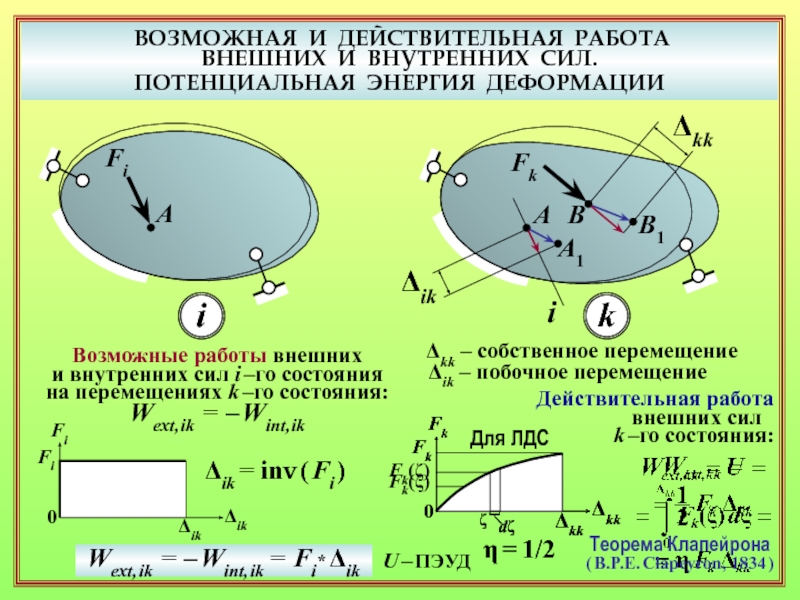
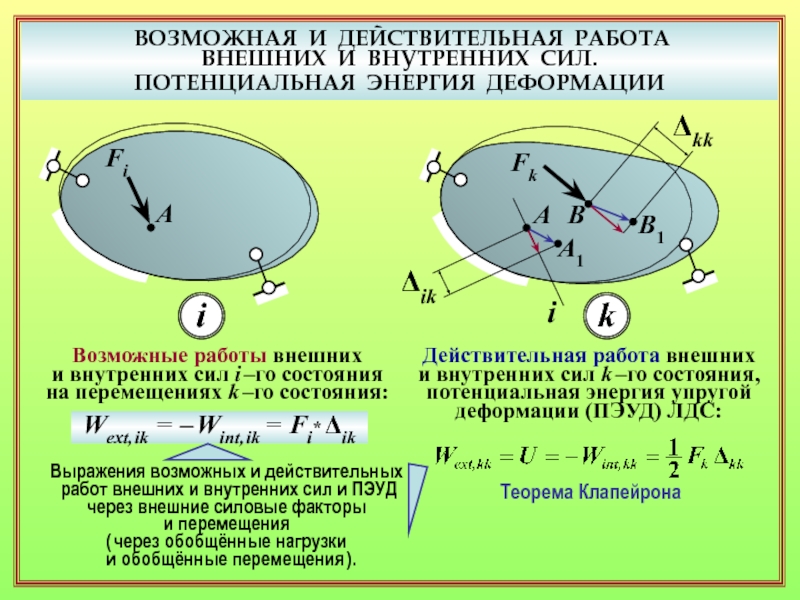
и ПЭУД через обобщённые нагрузки и обобщённые перемещения? Частный случай – линейно деформируемые системы ( теорема Клапейрона ). ( 10 – 12 )
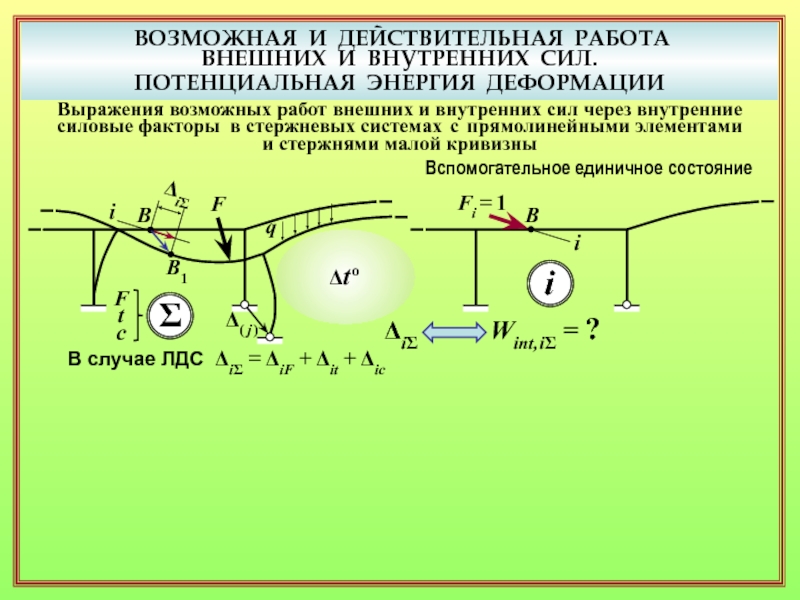
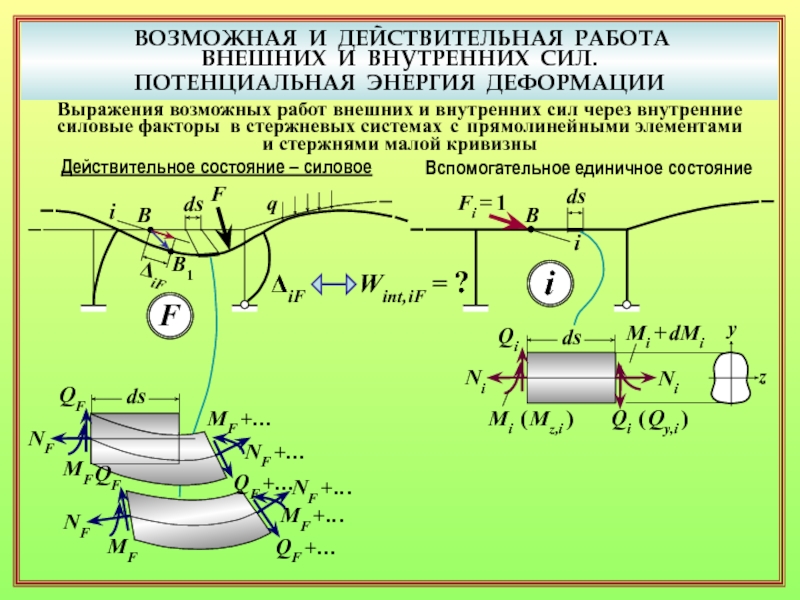
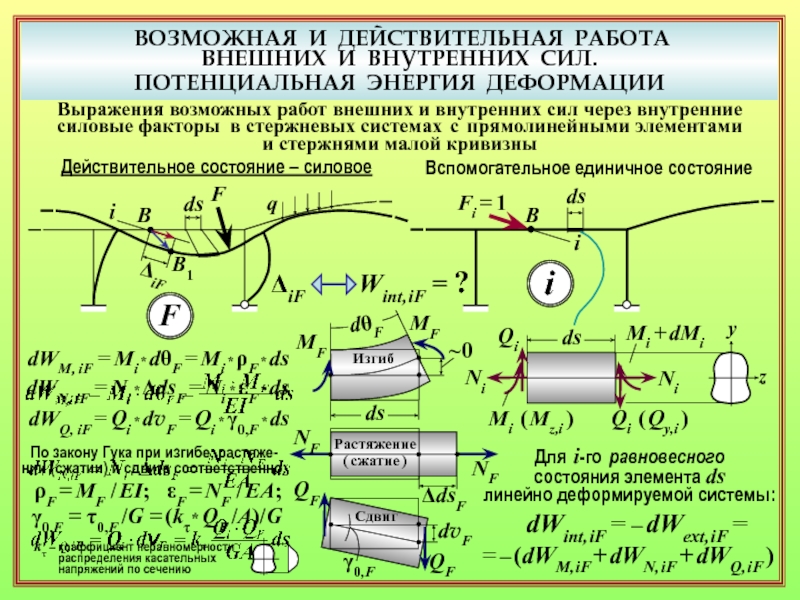
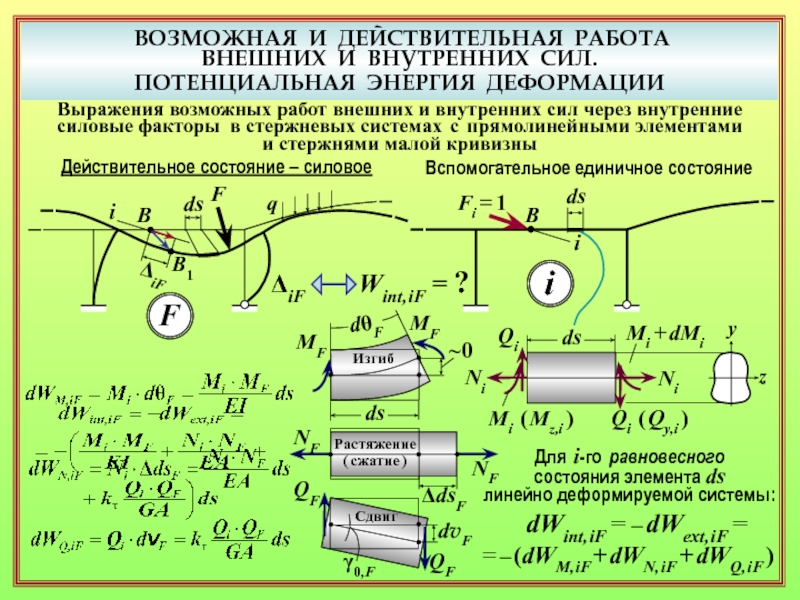
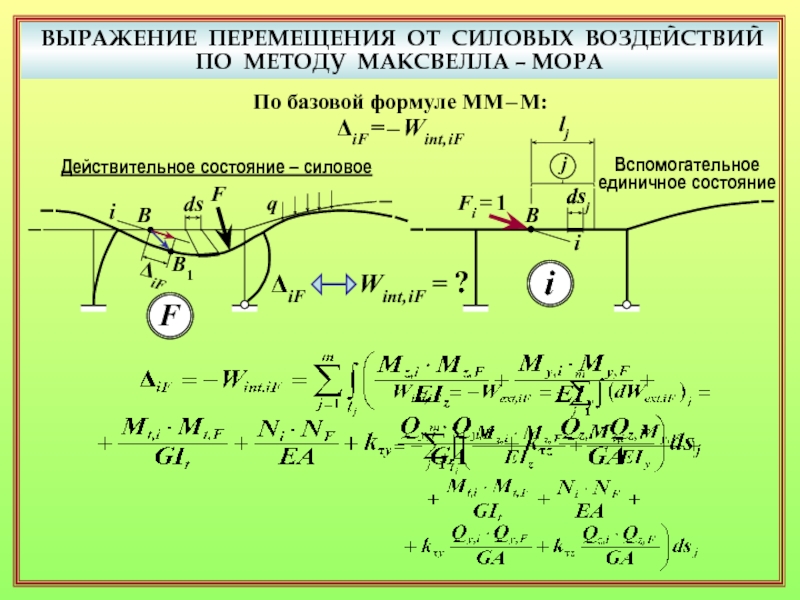
14. Какой приём используется для получения выражения возможной работы через внутренние силовые факторы? ( 16 )
15. Как деформации действительного силового состояния выражаются через внутренние силовые факторы? ( 18 )
16. Каков смысл величин EI, EA, GIt , GA/kτ , входящих в формулу Максвелла – Мора? ( 18 )
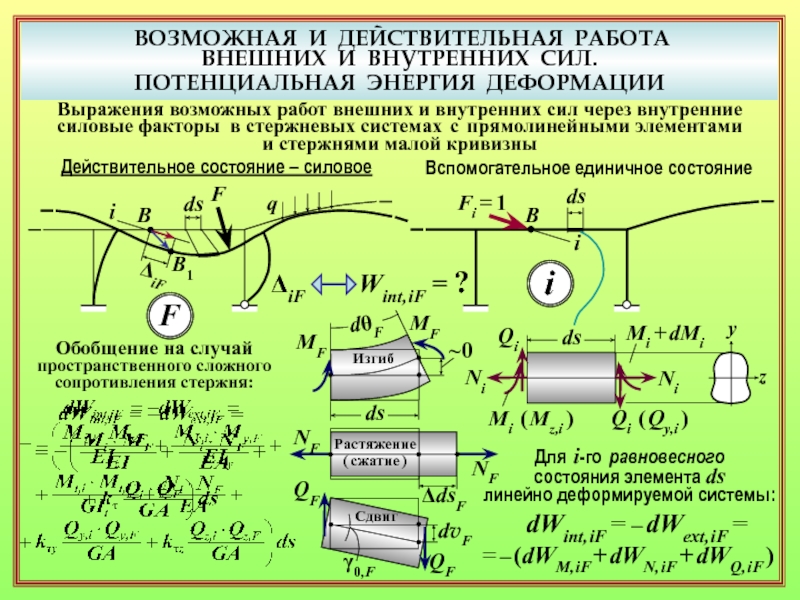
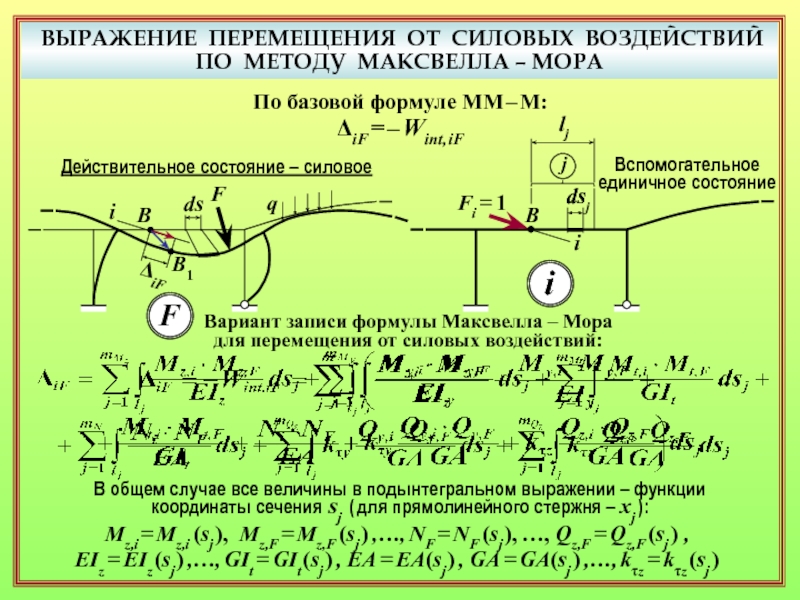
17. Варианты развёрнутой записи формулы Максвелла – Мора для перемещения
от силовых воздействий. ( 22, 23 )
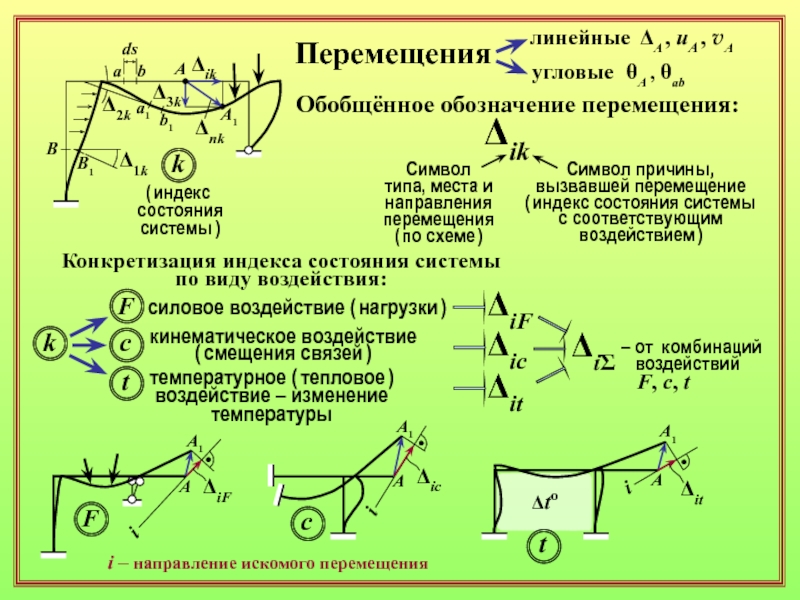
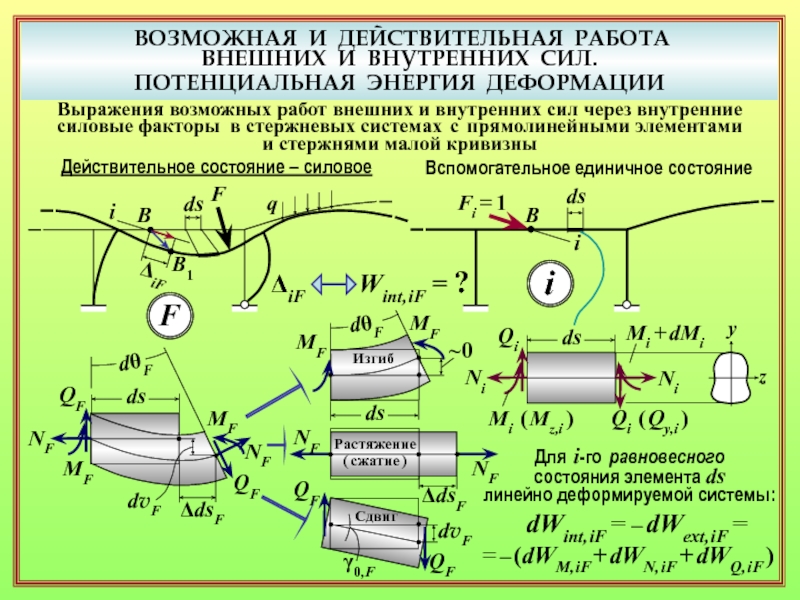
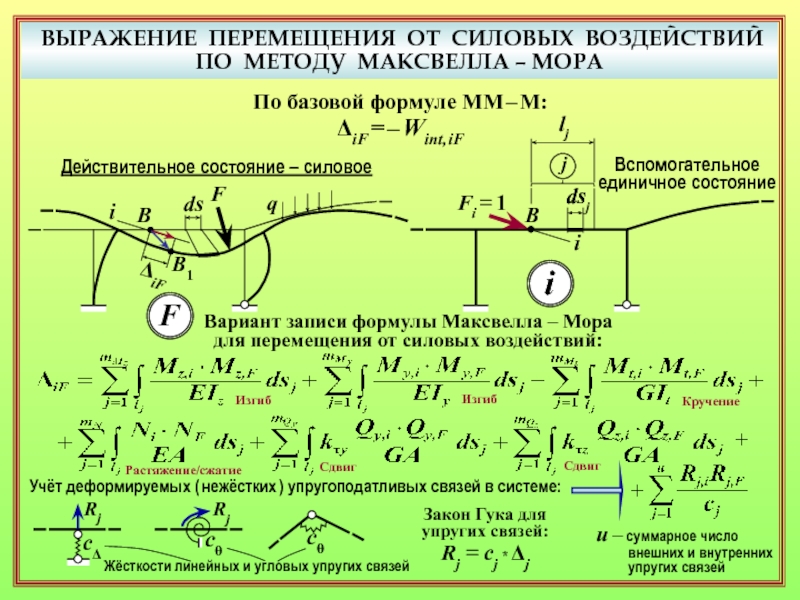
18. Какими слагаемыми в формуле Максвелла – Мора учитываются разные виды упругих деформаций элементов ( изгиб, растяжение/сжатие, сдвиг, кручение )? ( 24 )
19. Что учитывает коэффициент kτ в слагаемом формулы Максвелла – Мора, отражающем
влияние сдвига? ( 18 ) влияние сдвига? ( 18 ) ( 27 )
20. Как учитываются в формуле Максвелла – Мора деформации упругоподатливых связей системы? ( 24 )
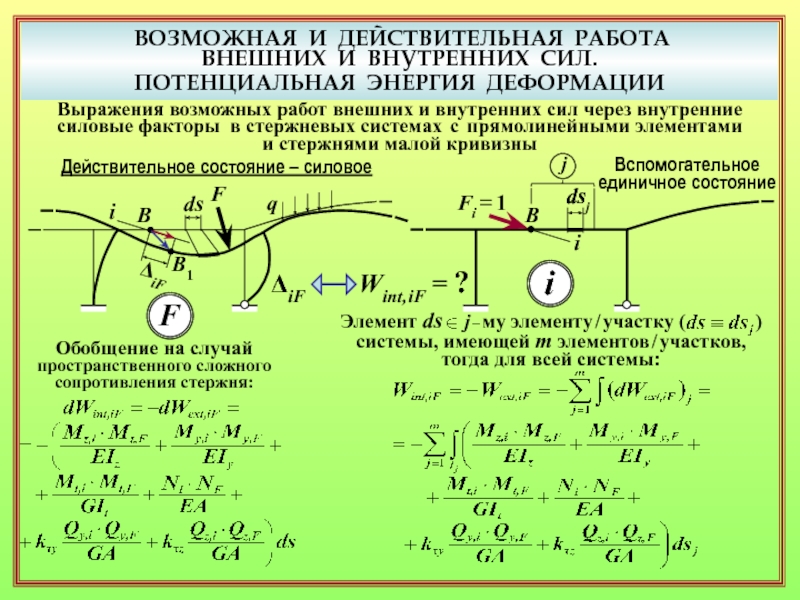
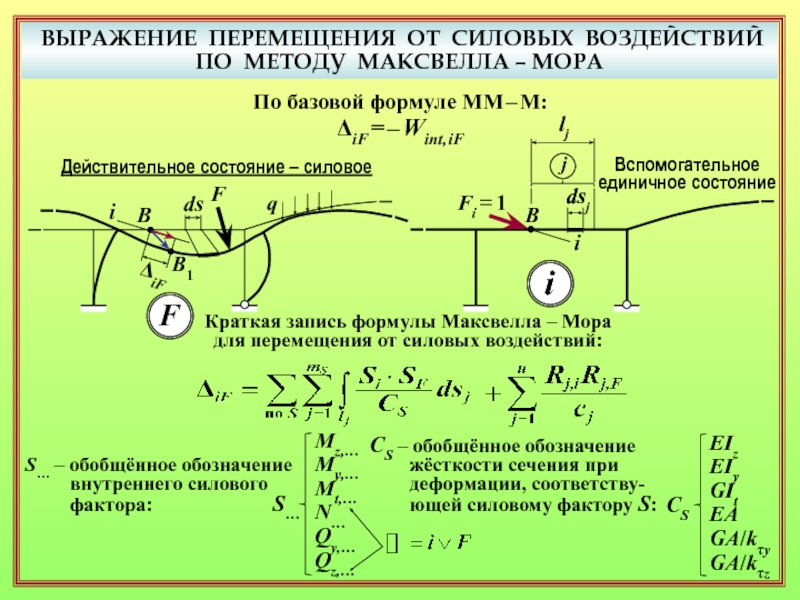
21. Краткая обобщённая запись формулы Максвелла – Мора для перемещения от силового
воздействия. ( 25 )
22. Какие величины обобщённо обозначаются как Si и SF в краткой записи формулы Максвелла – Мора? То же, СS? ( 25 )
_____________________________________________________
*) Только в режиме «Показ слайдов»