сечением
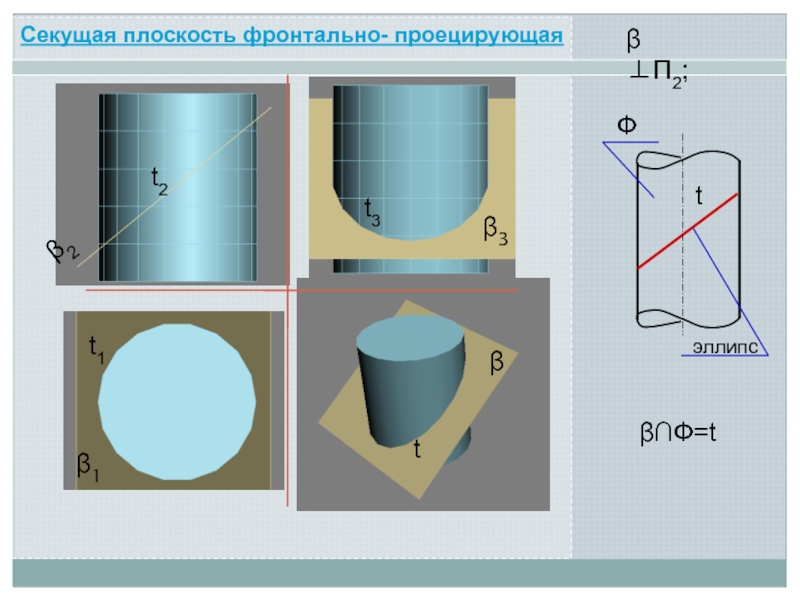
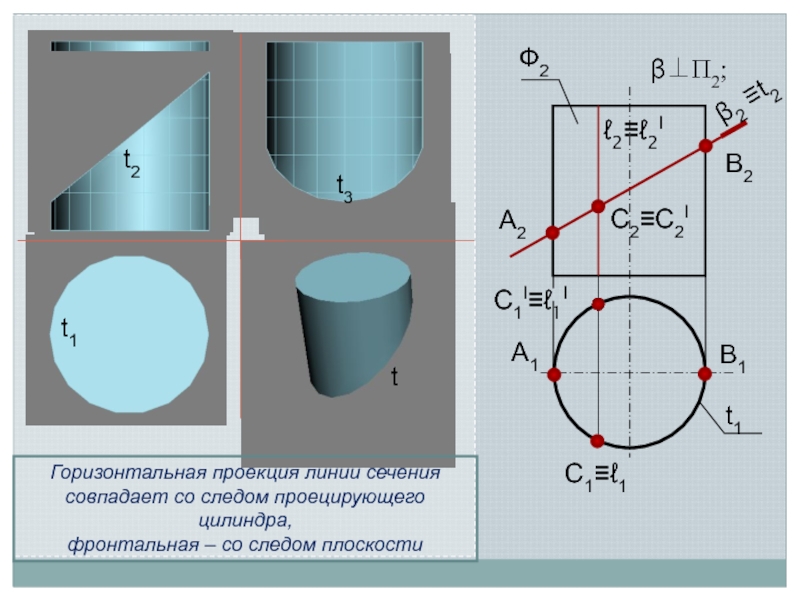
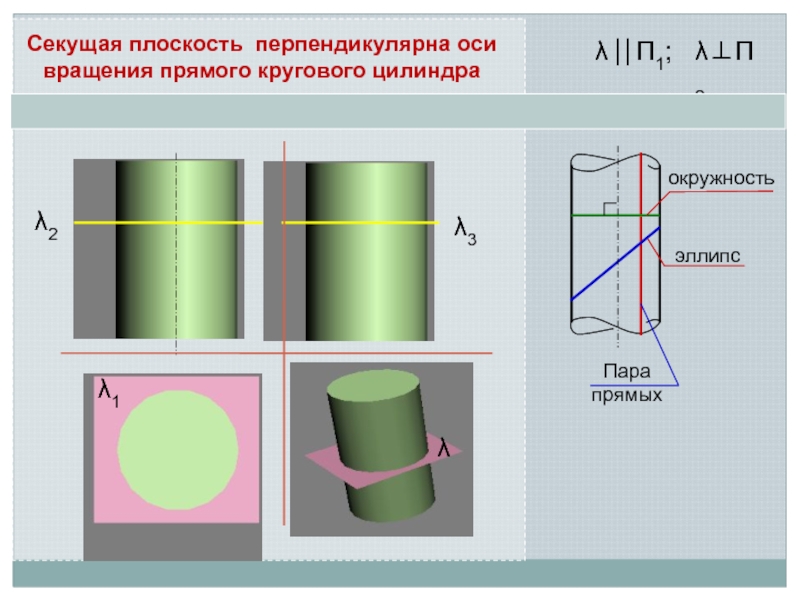
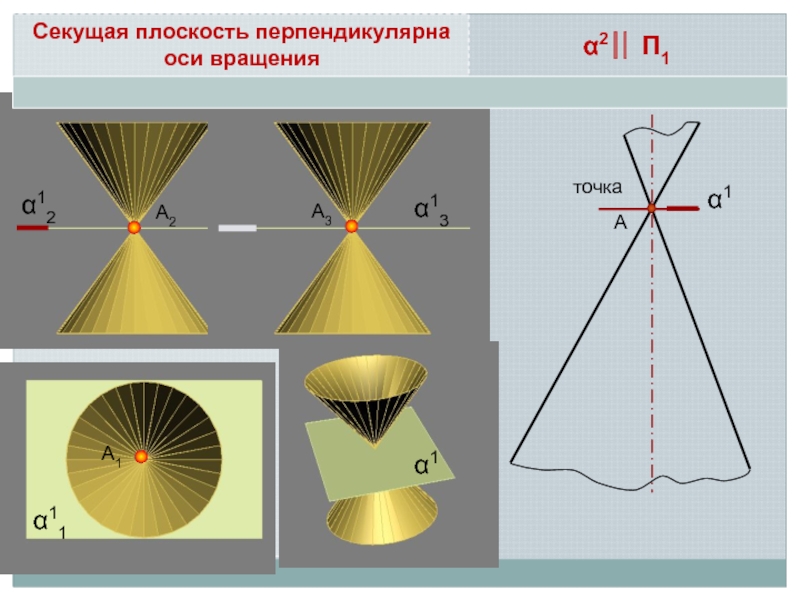
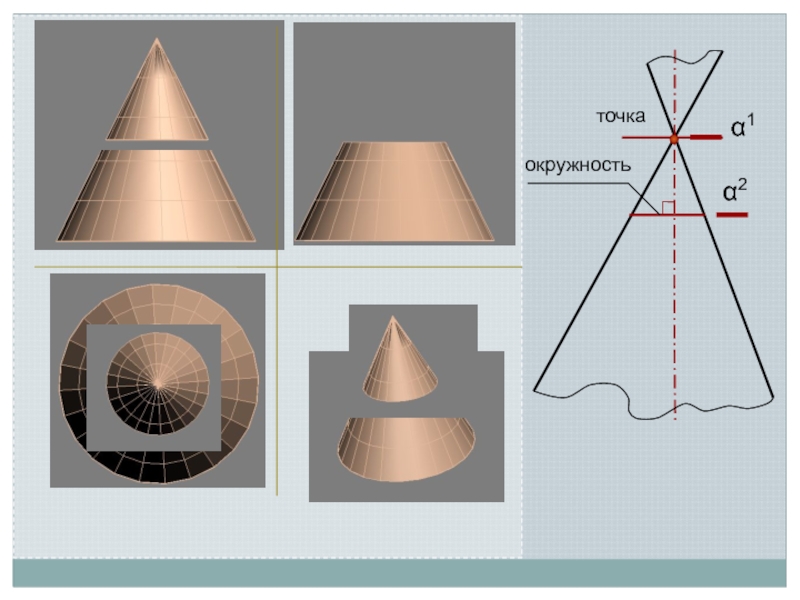
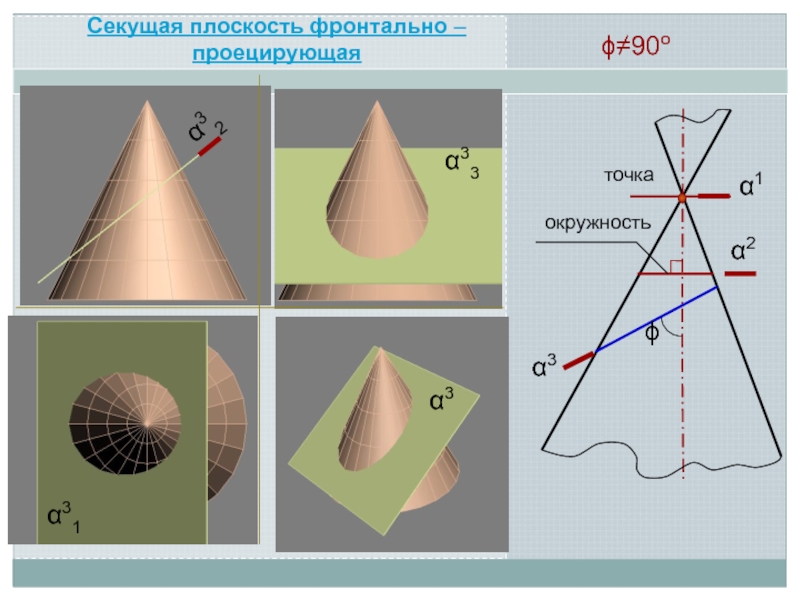
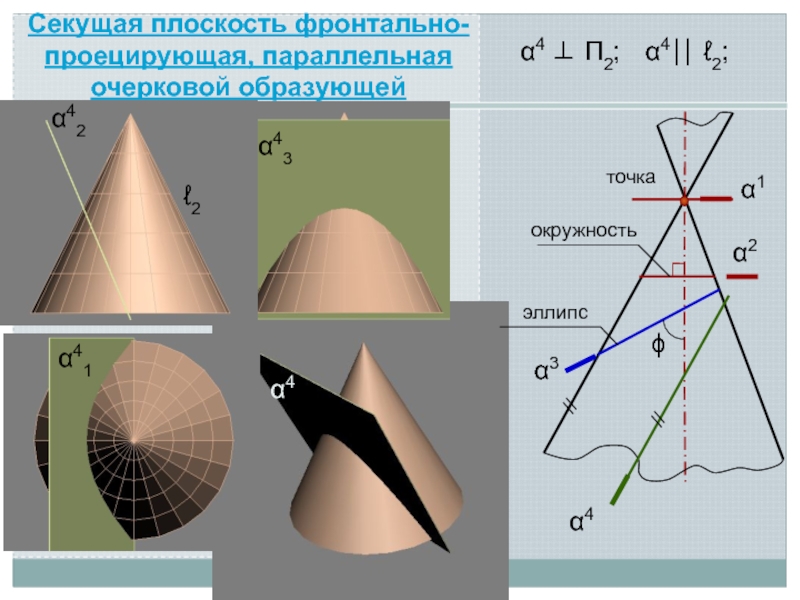
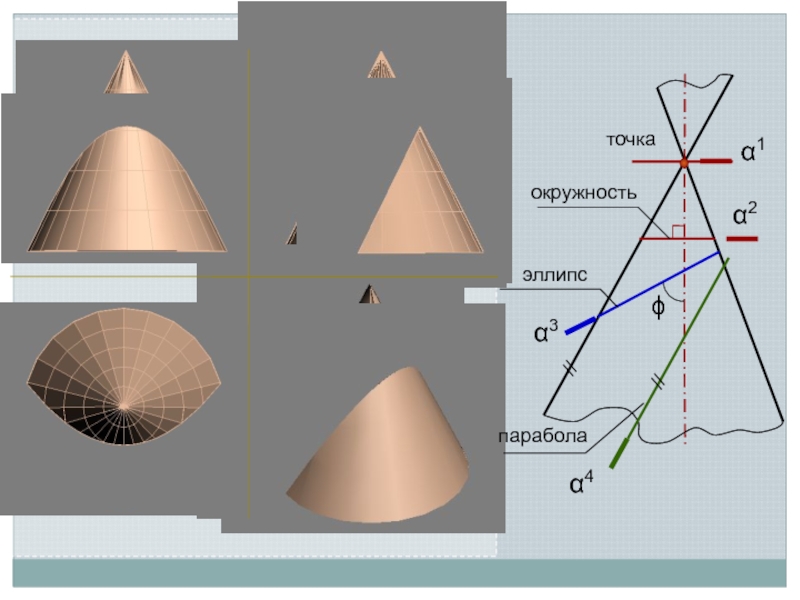
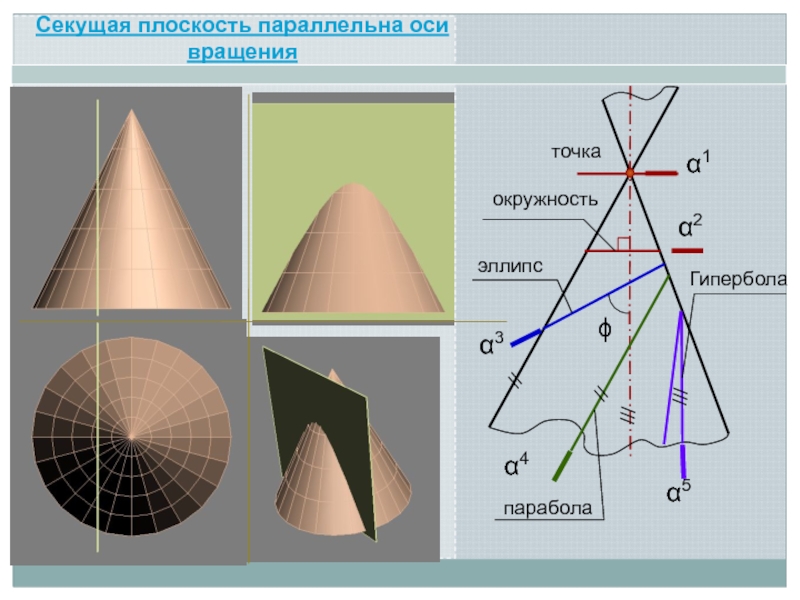
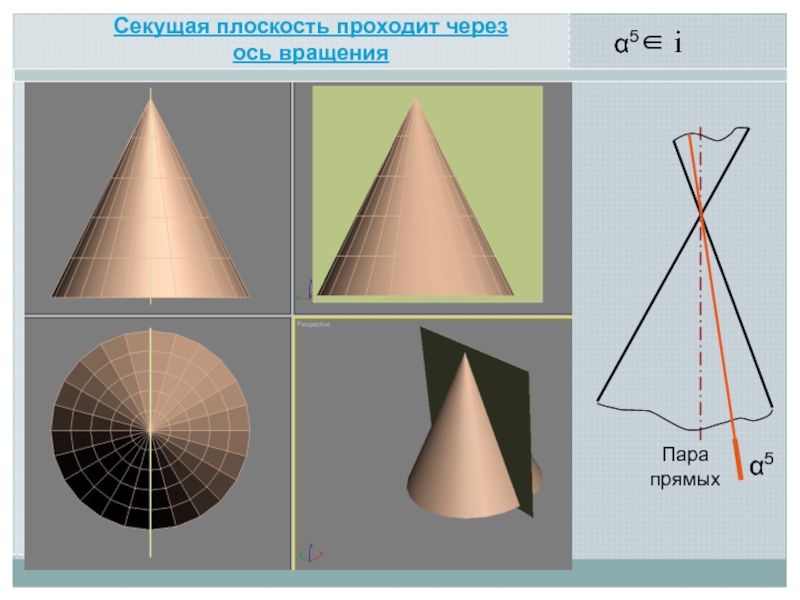
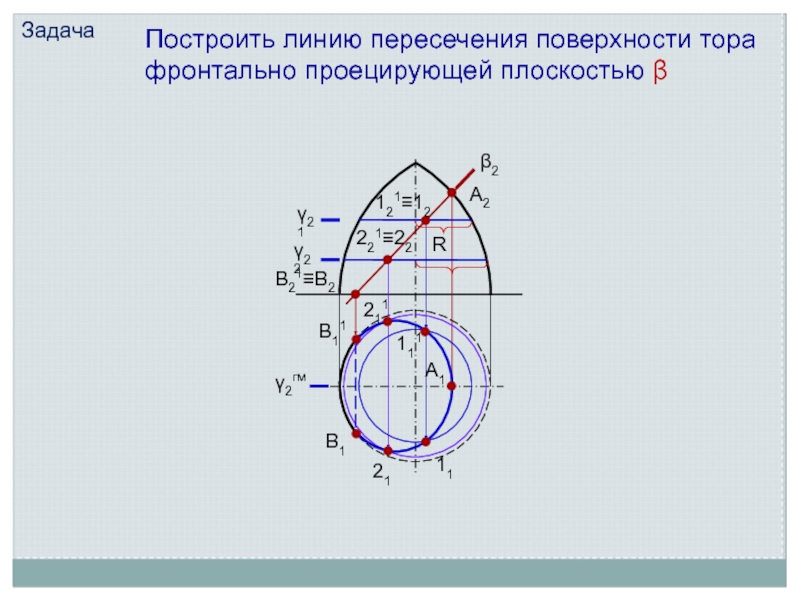
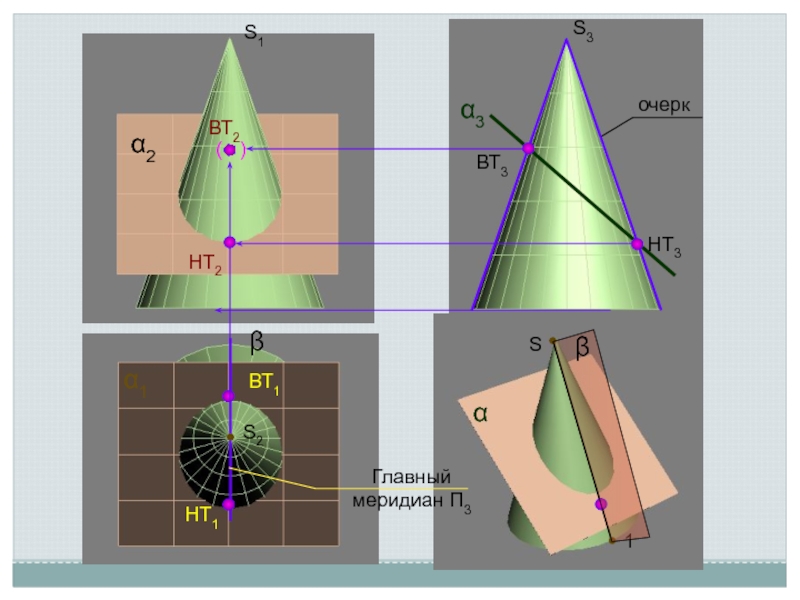
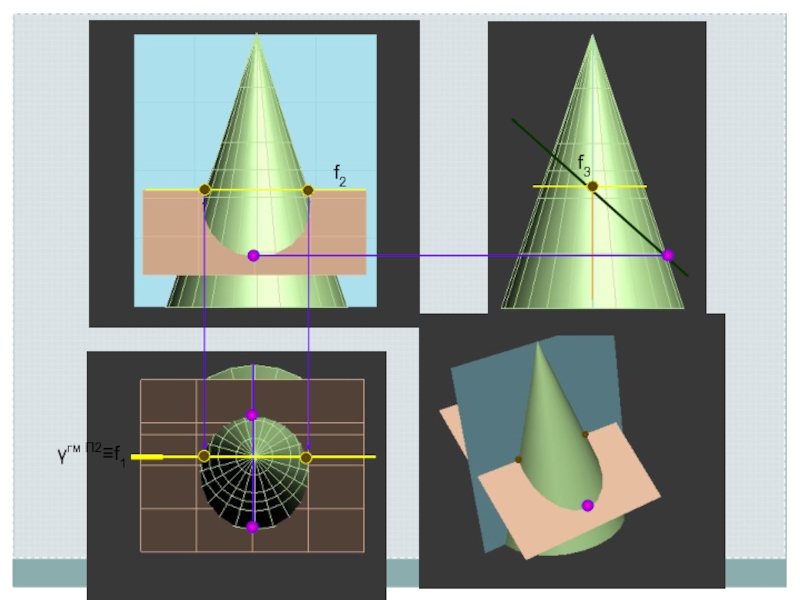
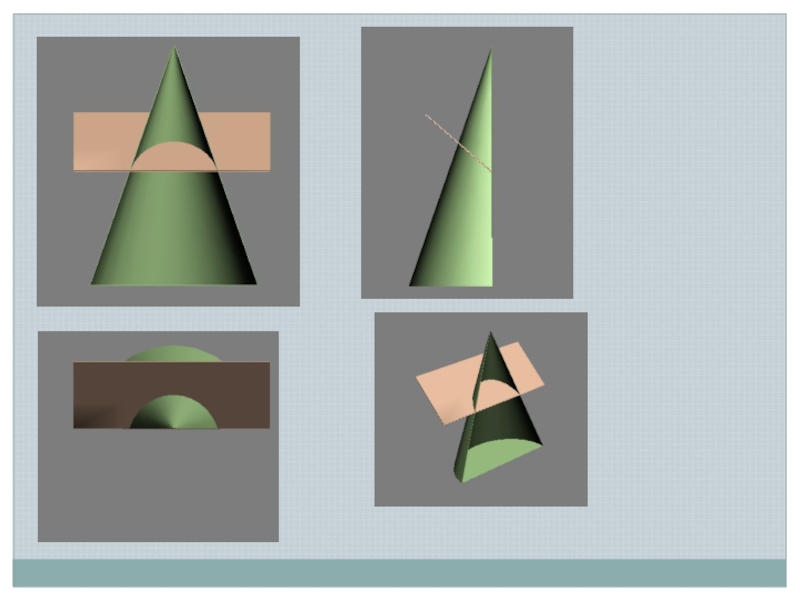
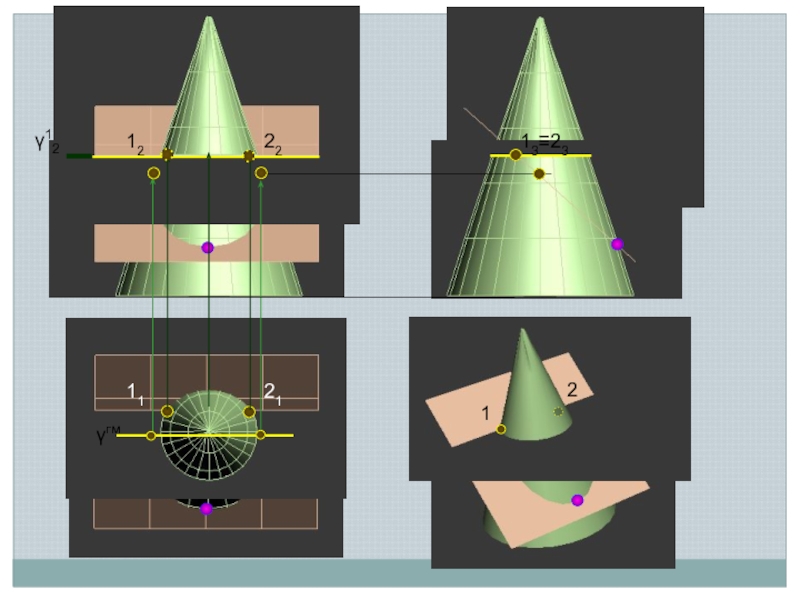
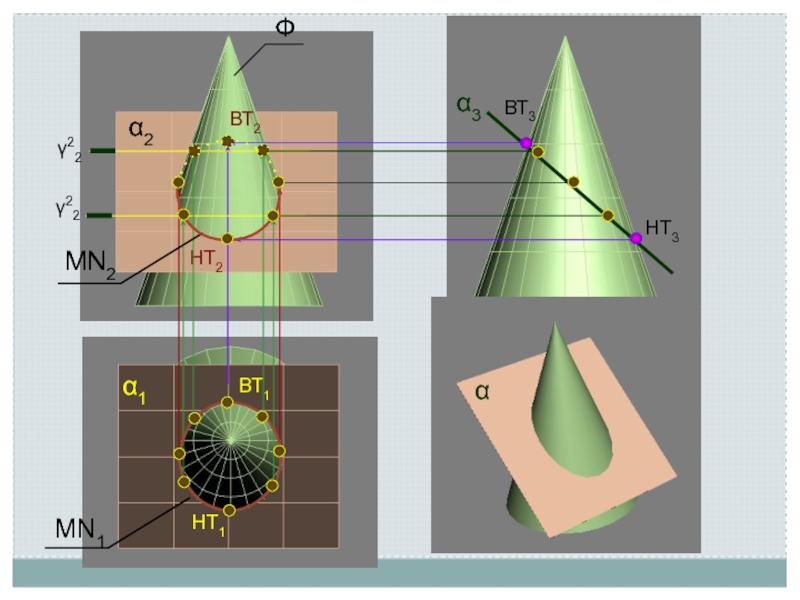
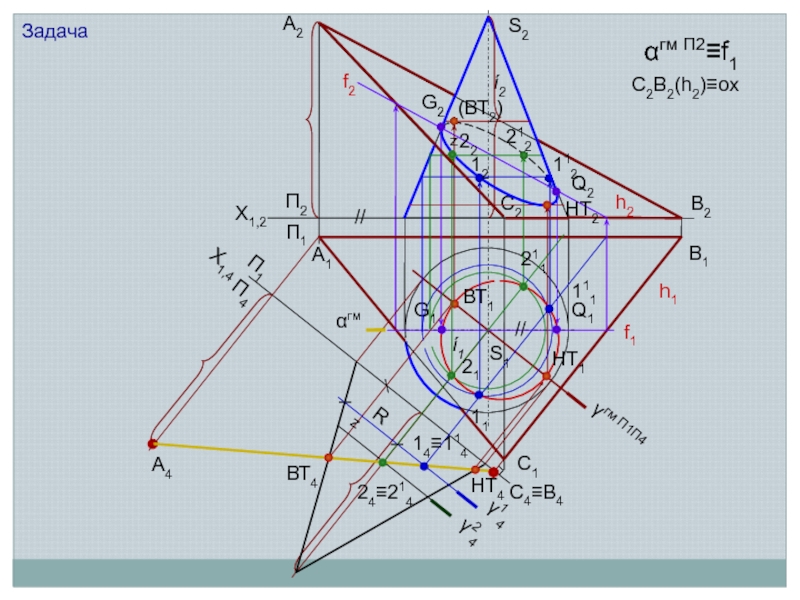
Линия пересечения поверхности с плоскостью является линией, одновременно принадлежащей поверхности
и секущей плоскости
Поэтому для ее построения необходимо отыскать такие точки и линии, которые одновременно принадлежат данной поверхности и заданной секущей плоскости