Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Перпендикулярность прямых и плоскостей
Содержание
- 1. Перпендикулярность прямых и плоскостей
- 2. ПланПерпендикулярность прямыхПерпендикулярность прямой и плоскостиПризнак перпендикулярности прямой
- 3. Продолжение плана7. Куб, его перпендикулярные прямые, наклонные
- 4. Перпендикулярность пря- мых в пространствеДве пересекающиеся прямые
- 5. Перпендикулярные прямыеДве скрещивающиеся прямые называются перпендикулярными, если параллельные им пересекающиеся прямые перпендикулярны.Аbb’a
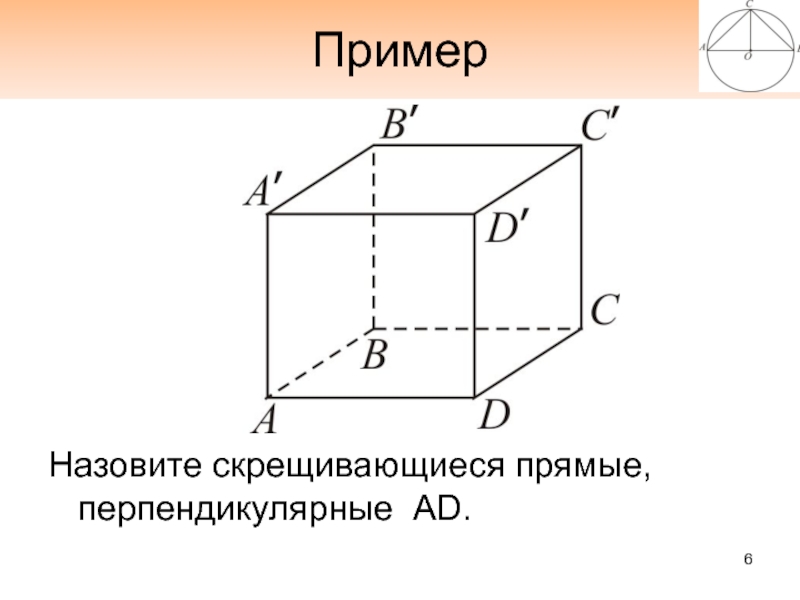
- 6. ПримерНазовите скрещивающиеся прямые, перпендикулярные AD.
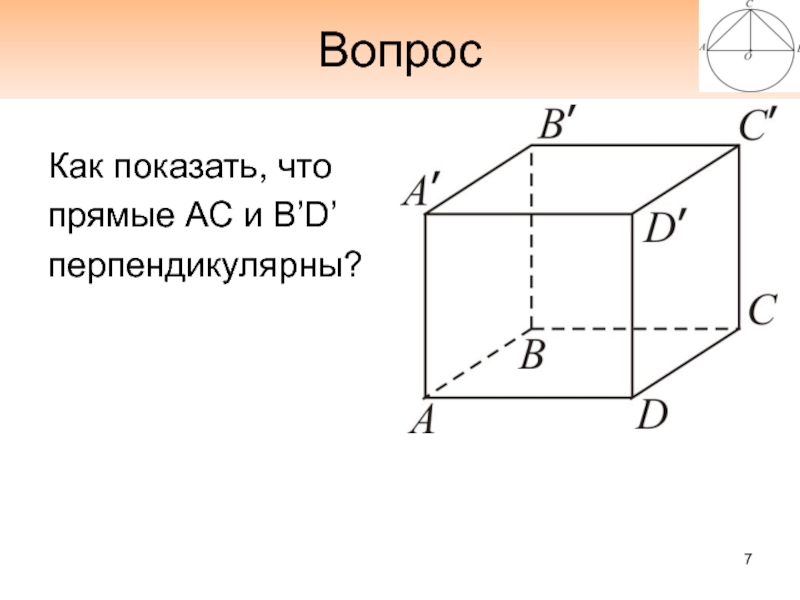
- 7. ВопросКак показать, чтопрямые АС и B’D’перпендикулярны?
- 8. ТеоремаЕсли две пересекающиеся прямые соответственно параллельны двум
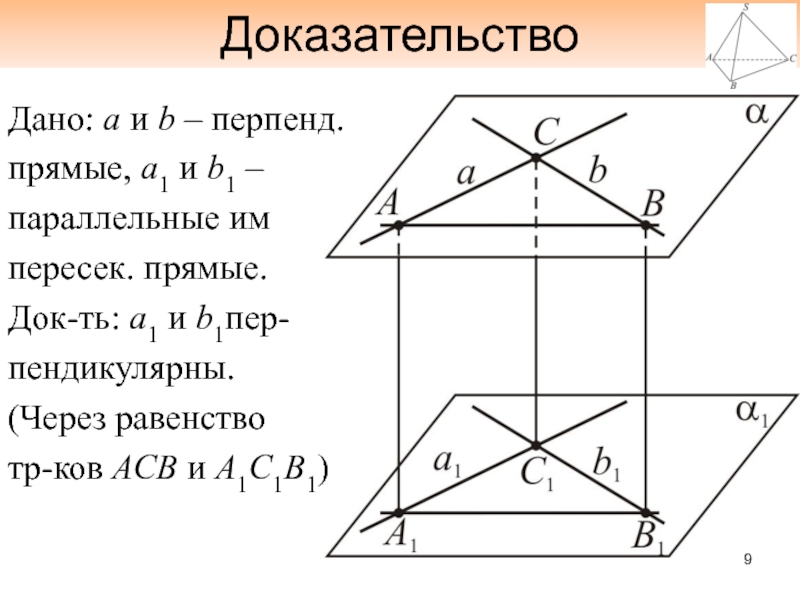
- 9. ДоказательствоДано: а и b – перпенд.прямые, а1
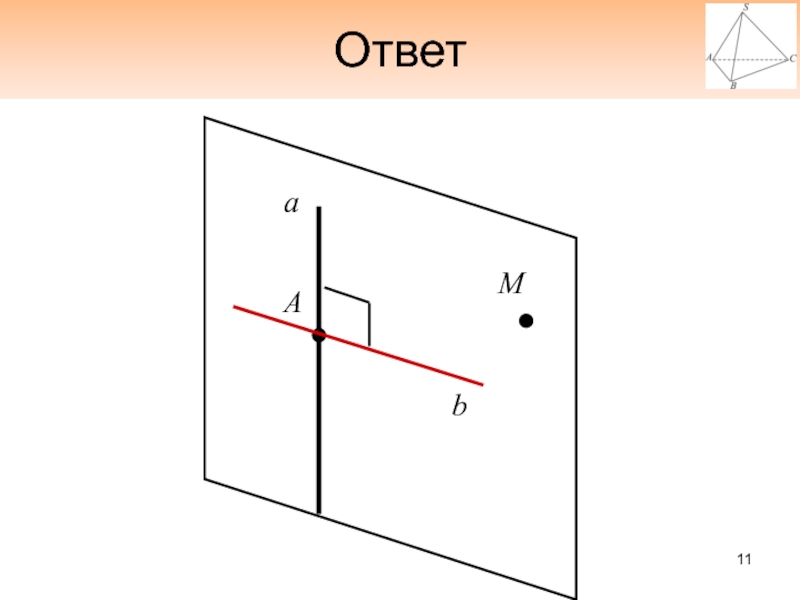
- 10. 1. Задача на построениеМожно ли через любую
- 11. ОтветМАbа
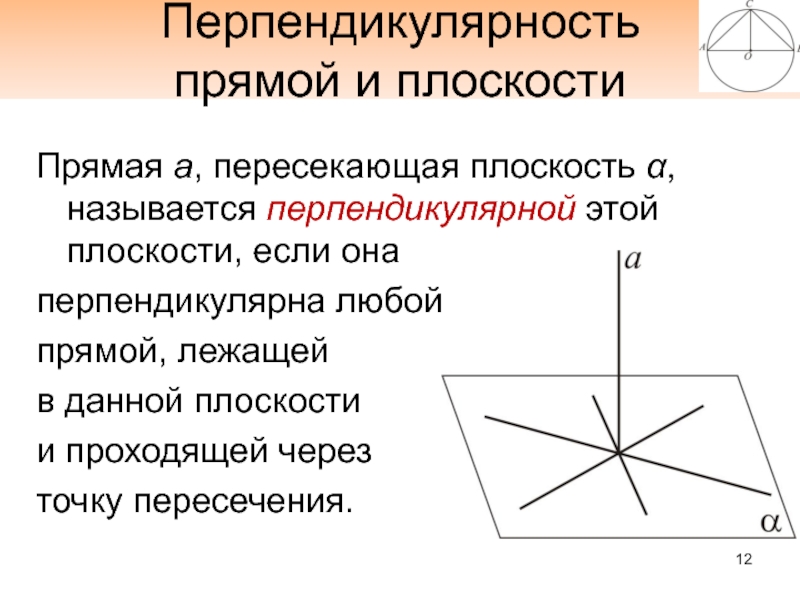
- 12. Перпендикулярность прямой и плоскостиПрямая а, пересекающая плоскость
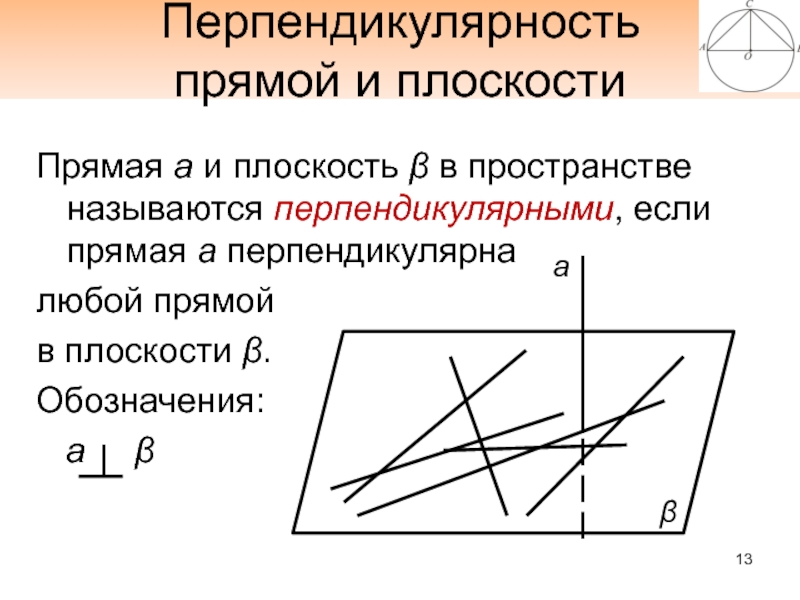
- 13. Перпендикулярность прямой и плоскостиПрямая а и плоскость
- 14. Перпендикулярность прямой и плоскости обозначается знаком .
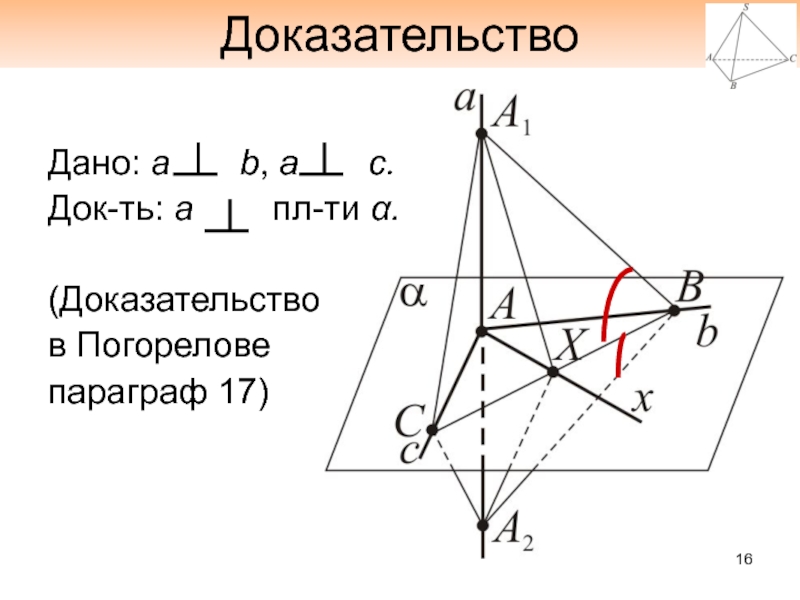
- 15. Признак перпендикулярности прямой и плоскостиЕсли две пересекающие
- 16. ДоказательствоДано: а b, а
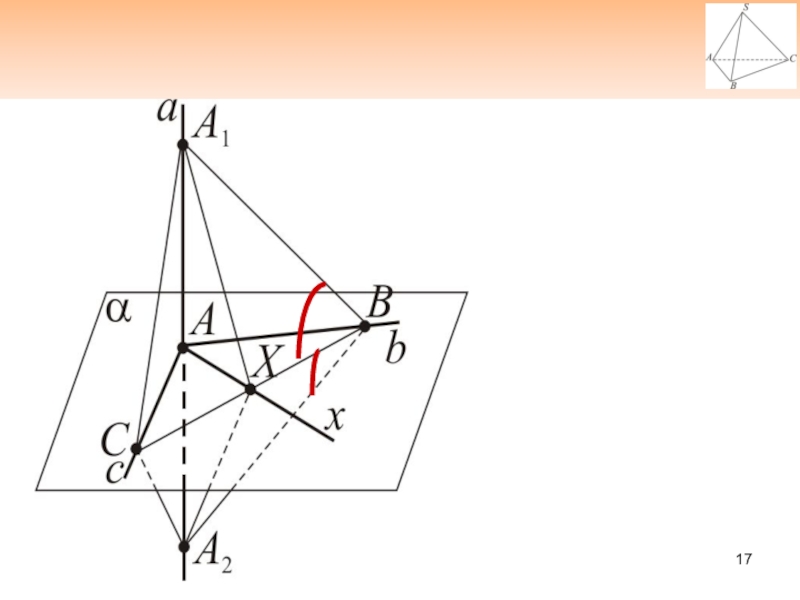
- 17. Слайд 17
- 18. Свойства перпендикулярной прямой и плоскостиТ.1. Если плоскость
- 19. Свойства перпендикулярной прямой и плоскостиТ.2. Две прямые,
- 20. Теорема 3. Если пря-мая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой плоскости.
- 21. Обратное утверждениеВерно обратное свойство.Если прямая перпендикулярна двум различным плоскостям, то эти плоскости параллельны.
- 22. Задача на построениеКак через данную точку на ребре кубапровести плоскость, перпендикулярнуюпрямой АС?МК
- 23. Перпендикуляр и наклоннаяПусть дана плоскость и точка
- 24. Перпендикуляр и наклоннаяТочка В называется основанием этого
- 25. Перпендикуляр и наклоннаяТочка С называется основанием наклонной.Отрезок,
- 26. Определение наклоннойНаклонной, проведеннойиз данной точки к даннойплоскости,
- 27. Свойство перпендикуляра и наклоннойДлина перпендикуляра, проведенного из
- 28. Расстояние от точки до плоскостиРасстоянием от точки
- 29. ВопросыДана точка М и плоскость α. Сколько
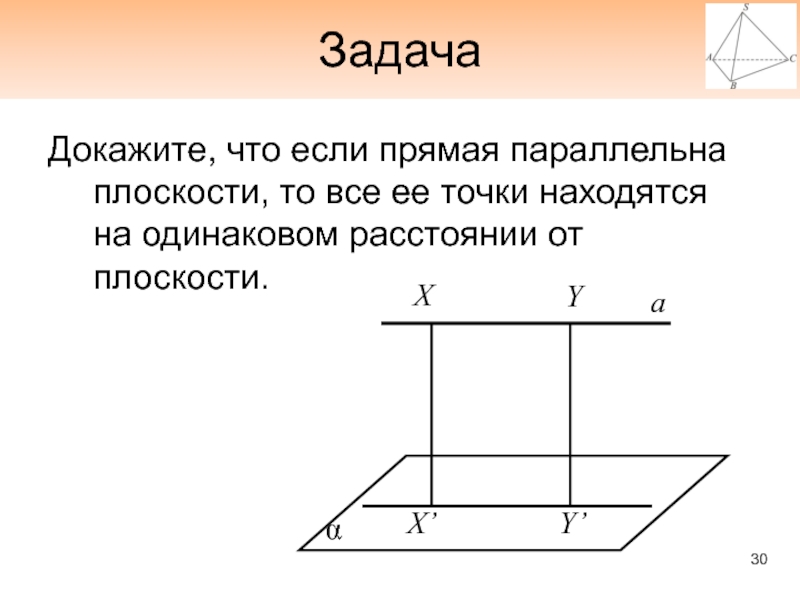
- 30. ЗадачаДокажите, что если прямая параллельна плоскости, то все ее точки находятся на одинаковом расстоянии от плоскости.
- 31. Теорема о трех перпендикулярахПрямая теорема. Прямая, проведеннаяна
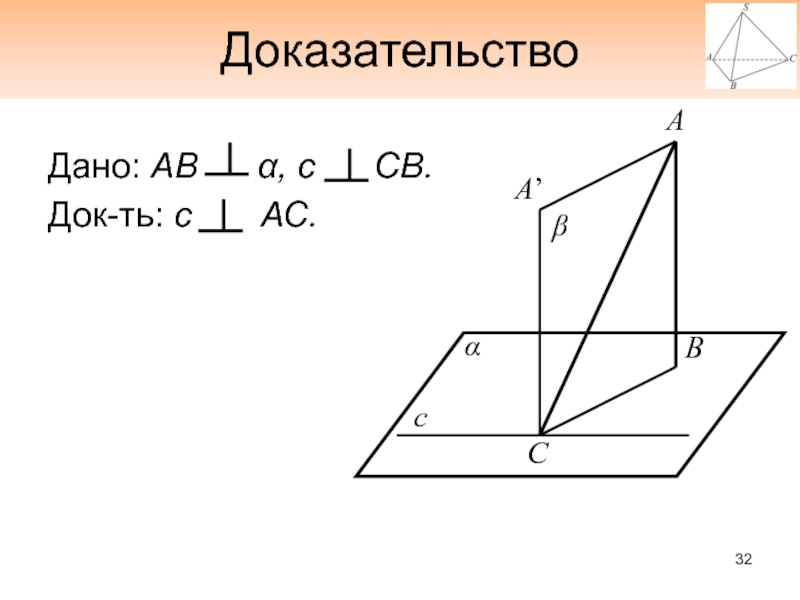
- 32. ДоказательствоДано: АВ α, с СВ. Док-ть: с АС.
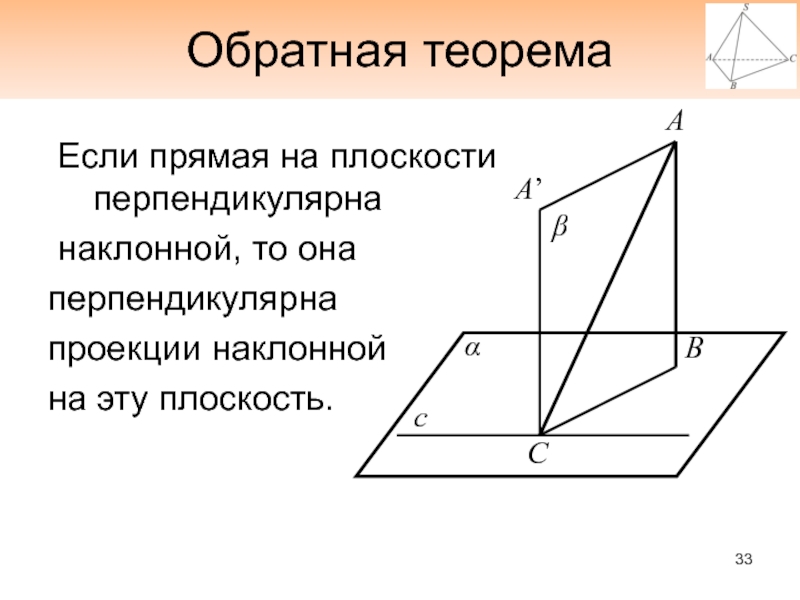
- 33. Обратная теорема Если прямая на плоскости перпендикулярна наклонной, то онаперпендикулярнапроекции наклоннойна эту плоскость.
- 34. Задача (устно)
- 35. ЛитератураУчебник по геометрии под ред. Погорелова
- 36. Домашнее задание1. Выучить определение прямой, перпендикулярной плоскости2.
- 37. Скачать презентанцию
ПланПерпендикулярность прямыхПерпендикулярность прямой и плоскостиПризнак перпендикулярности прямой и плоскостиПерпендикуляр и наклоннаяРасстояние от точки до плоскостиТеорема о трех перпендикулярах
Слайды и текст этой презентации
Слайд 2План
Перпендикулярность прямых
Перпендикулярность прямой и плоскости
Признак перпендикулярности прямой и плоскости
Перпендикуляр и
наклонная
Слайд 3Продолжение плана
7. Куб, его перпендикулярные прямые, наклонные и их проекции
8.
Треугольная пирамида, прямая призма и проектирование точек на плоскость
9. Перпендикулярность
плоскостей10. Признак перпендикулярности плоскостей
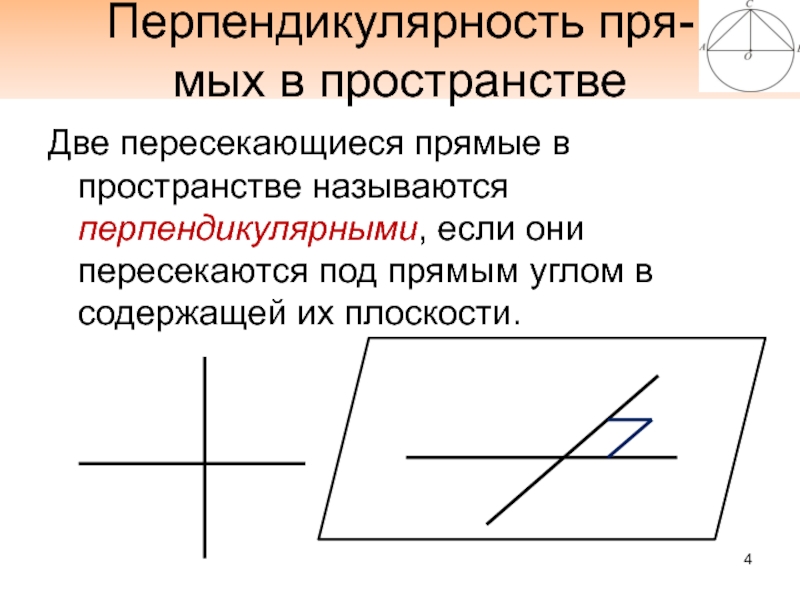
Слайд 4Перпендикулярность пря-
мых в пространстве
Две пересекающиеся прямые в пространстве называются перпендикулярными,
если они пересекаются под прямым углом в содержащей их плоскости.
Слайд 5Перпендикулярные прямые
Две скрещивающиеся прямые называются перпендикулярными, если параллельные им пересекающиеся
прямые перпендикулярны.
А
b
b’
a
Слайд 8Теорема
Если две пересекающиеся прямые соответственно параллельны двум перпендикулярным прямым, то
они тоже перпендикулярны.
Доказательство в Погорелове в параграфе «Перпендикулярность прямых и
плоскостей», теорема 17.1
Слайд 9Доказательство
Дано: а и b – перпенд.
прямые, а1 и b1 –
параллельные
им
пересек. прямые.
Док-ть: а1 и b1пер-
пендикулярны.
(Через равенство
тр-ков АСВ и А1С1В1)
Слайд 101. Задача на построение
Можно ли через любую точку прямой в
пространстве провести перпендикулярную ей прямую?
Если да, то сколько?
Слайд 12Перпендикулярность
прямой и плоскости
Прямая а, пересекающая плоскость α, называется перпендикулярной этой
плоскости, если она
перпендикулярна любой
прямой, лежащей
в данной плоскости
и проходящей через
точку пересечения.
Слайд 13Перпендикулярность
прямой и плоскости
Прямая а и плоскость β в пространстве называются
перпендикулярными, если прямая а перпендикулярна
любой прямой
в плоскости β.
Обозначения:
а
ββ
а
Слайд 15Признак перпендикулярности прямой и плоскости
Если две пересекающие прямые, лежащие в
плоскости β, перпендикулярны прямой а, то а
β.Другая формулировка.
Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости.
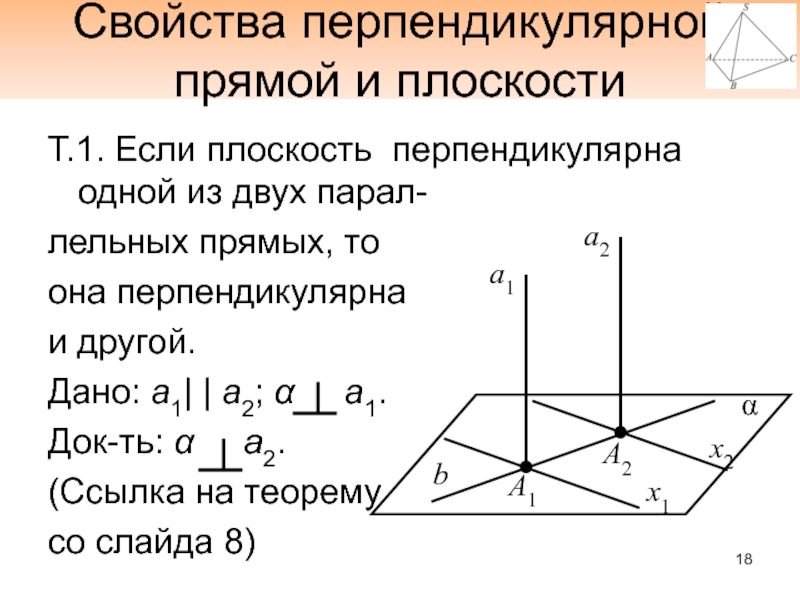
Слайд 18Свойства перпендикулярной прямой и плоскости
Т.1. Если плоскость перпендикулярна одной
из двух парал-
лельных прямых, то
она перпендикулярна
и другой.
Дано: а1| | a2;
α а1.Док-ть: α а2.
(Ссылка на теорему
со слайда 8)
a1
a2
x2
x1
A2
A1
b
a
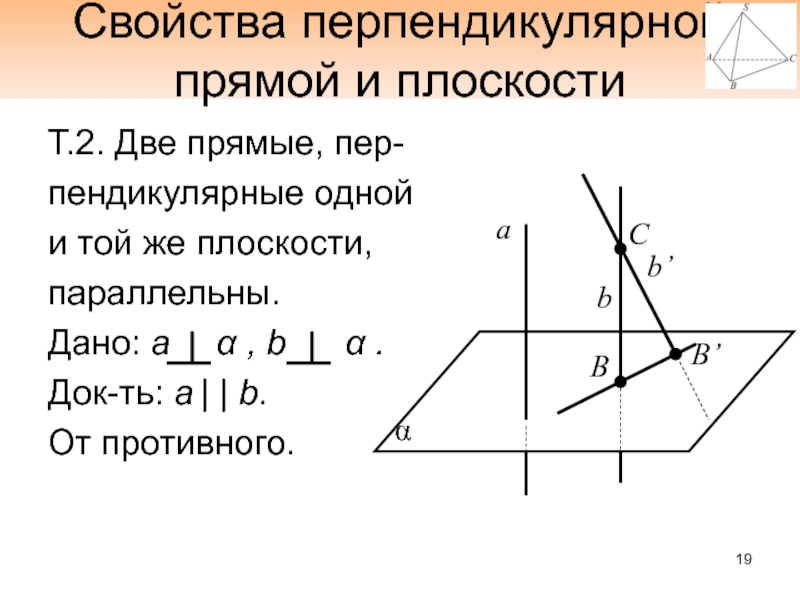
Слайд 19Свойства перпендикулярной прямой и плоскости
Т.2. Две прямые, пер-
пендикулярные одной
и той
же плоскости,
параллельны.
Дано: а α , b
α .Док-ть: а | | b.
От противного.
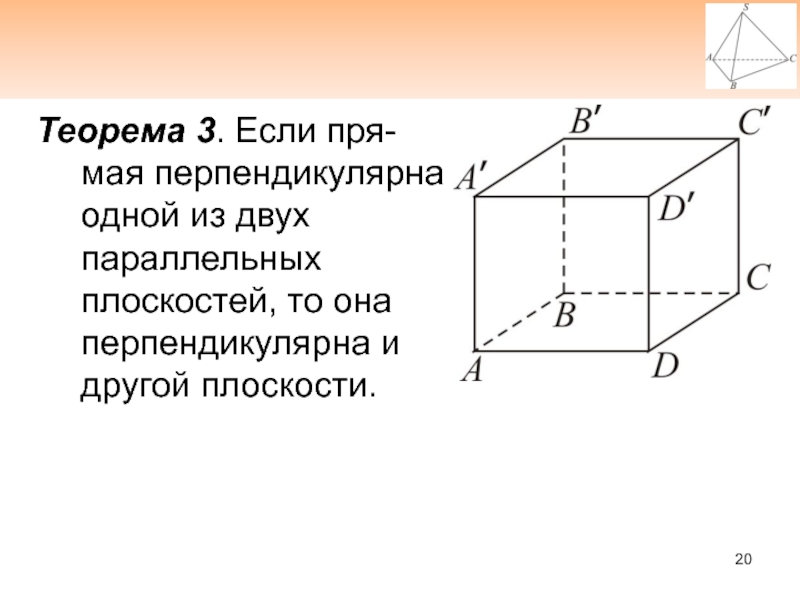
Слайд 20Теорема 3. Если пря-мая перпендикулярна одной из двух параллельных плоскостей,
то она перпендикулярна и другой плоскости.
Слайд 21Обратное утверждение
Верно обратное свойство.
Если прямая перпендикулярна двум различным плоскостям, то
эти плоскости параллельны.
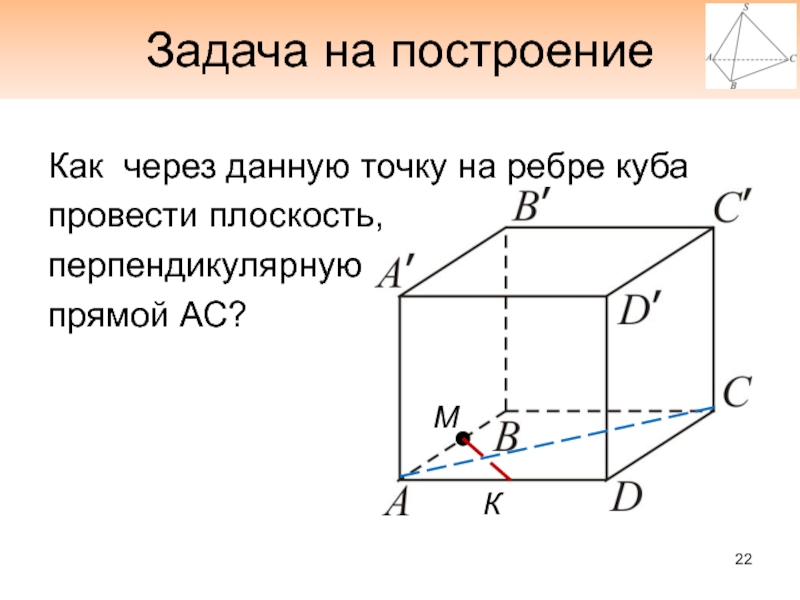
Слайд 22Задача на построение
Как через данную точку на ребре куба
провести плоскость,
перпендикулярную
прямой АС?
М
К
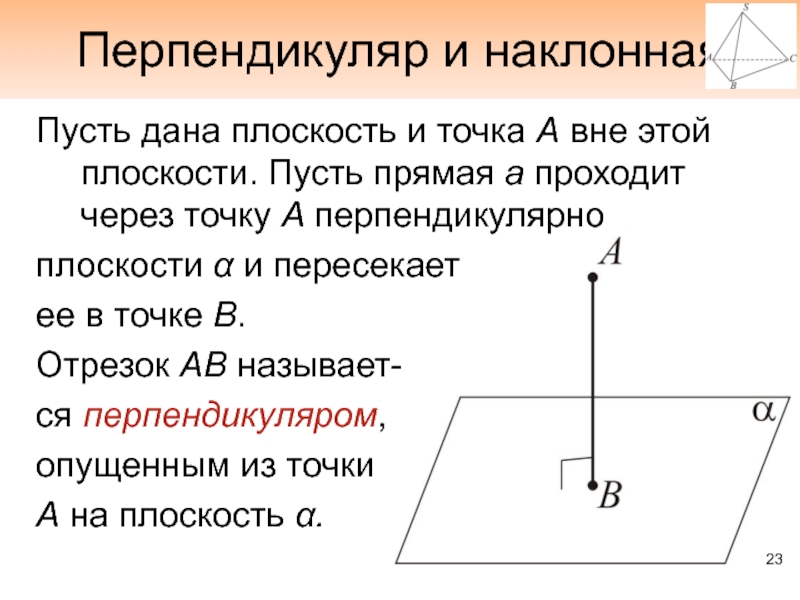
Слайд 23Перпендикуляр и наклонная
Пусть дана плоскость и точка А вне этой
плоскости. Пусть прямая а проходит через точку А перпендикулярно
плоскости α
и пересекаетее в точке В.
Отрезок АВ называет-
ся перпендикуляром,
опущенным из точки
А на плоскость α.
Слайд 24Перпендикуляр и наклонная
Точка В называется основанием этого перпендикуляра.
Пусть С –
любая точка
плоскости, отличная от В.
Отрезок АС называет-
ся наклонной, прове-
денной из
точки Ак плоскости α.
Слайд 25Перпендикуляр и наклонная
Точка С называется основанием наклонной.
Отрезок, соединяющий основания
перпендикуляра и
наклонной,
проведенных из одной и
той же точки, называется
проекцией наклонной
на плоскость α.
ВС – проекция АС.
Слайд 26Определение наклонной
Наклонной, проведенной
из данной точки к данной
плоскости, называется
любой отрезок, соеди-
няющий
данную
точку А с точкой плос-
кости, и не являющийся перпендикуляром.
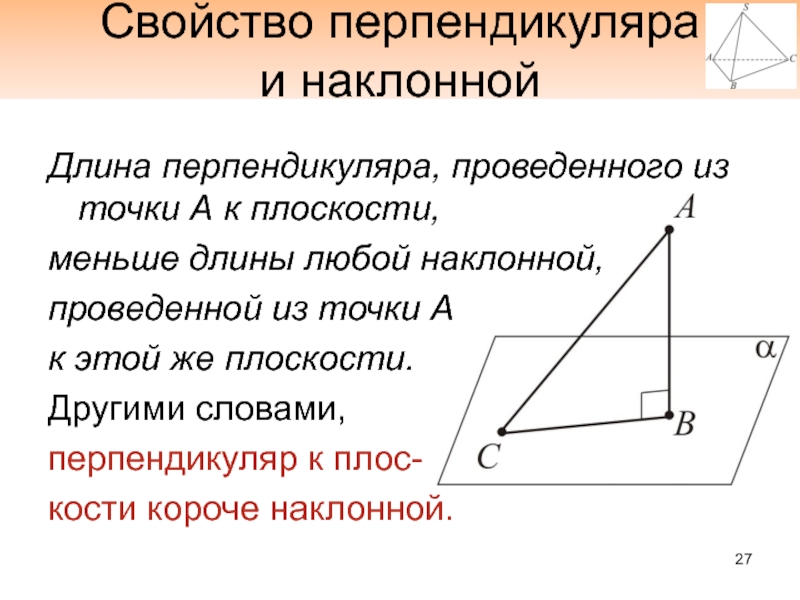
Слайд 27Свойство перпендикуляра
и наклонной
Длина перпендикуляра, проведенного из точки А к плоскости,
меньше длины любой наклонной,
проведенной из точки А
к этой же плоскости.
Другими
словами, перпендикуляр к плос-
кости короче наклонной.
Слайд 28Расстояние от точки
до плоскости
Расстоянием от точки М, не лежащей в
плоскости, до плоскости α называется длина перпендикуляра, проведенного из точки
М на данную плоскость.Найти расстояние от точки до плоскости – это значит найти длину перпендикуляра.
Слайд 29Вопросы
Дана точка М и плоскость α. Сколько можно построить перпендикуляров
из точки М к плоскости α?
Сколько можно построить наклонных из
точки М к этой плоскости?Сколько можно построить наклонных из точки М заданной длины?
Где лежат основания таких наклонных?
Слайд 30Задача
Докажите, что если прямая параллельна плоскости, то все ее точки
находятся на одинаковом расстоянии от плоскости.
Слайд 31Теорема о трех перпендикулярах
Прямая теорема. Прямая, проведенная
на плоскости через основание
наклон-
ной перпендикулярно ее проекции,
перпендикулярна и самой наклонной.
Слайд 33Обратная теорема
Если прямая на плоскости перпендикулярна
наклонной, то она
перпендикулярна
проекции
наклонной
на эту плоскость.
Слайд 36Домашнее задание
1. Выучить определение прямой, перпендикулярной плоскости
2. Выучить признак перпендикулярности
прямой и плоскости
3. Выучить теорему о трех перпендикулярах с доказательством
в обе стороны
