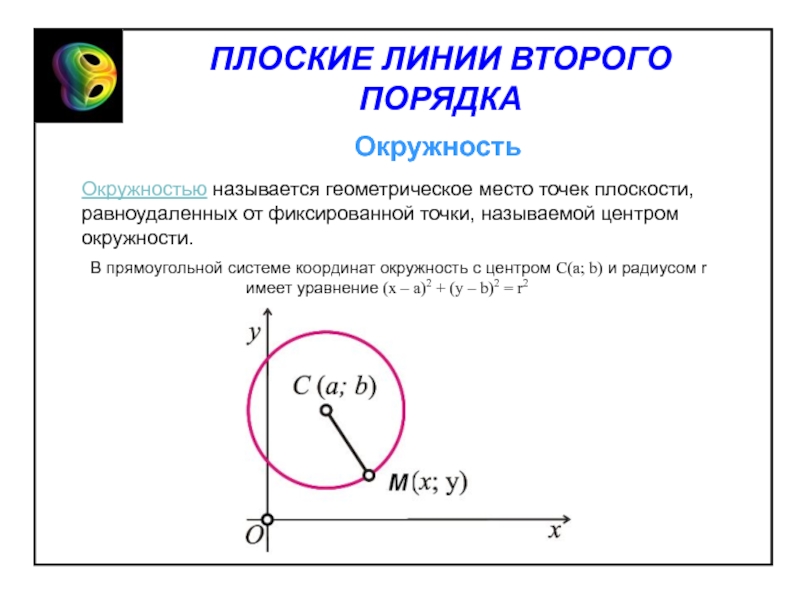
ПЛОСКИЕ ЛИНИИ ВТОРОГО ПОРЯДКА Окружность Окружностью называется геометрическое

Содержание

1. ПЛОСКИЕ ЛИНИИ ВТОРОГО ПОРЯДКА Окружность Окружностью называется геометрическое
2. АНИМАЦИЯ ПОСТРОЕНИЯ ЭЛЛИПСА!!!
3. Слайд 3
4. Выберем систему координат так,
5. Слайд 5
6. Таким образом, эллипс симметричен относительно
7. прямоугольника, образованного прямыми x= ± a и
8. Слайд 8
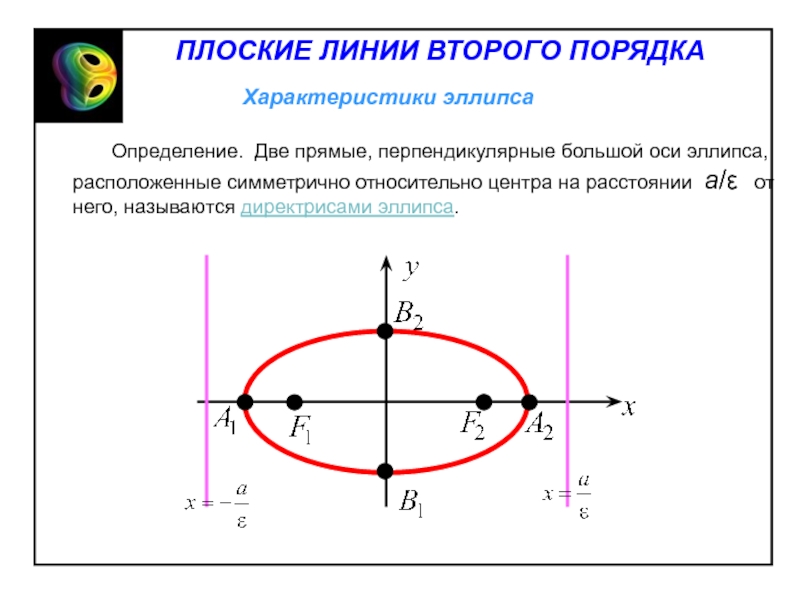
9. Определение. Две прямые,
10. Слайд 10
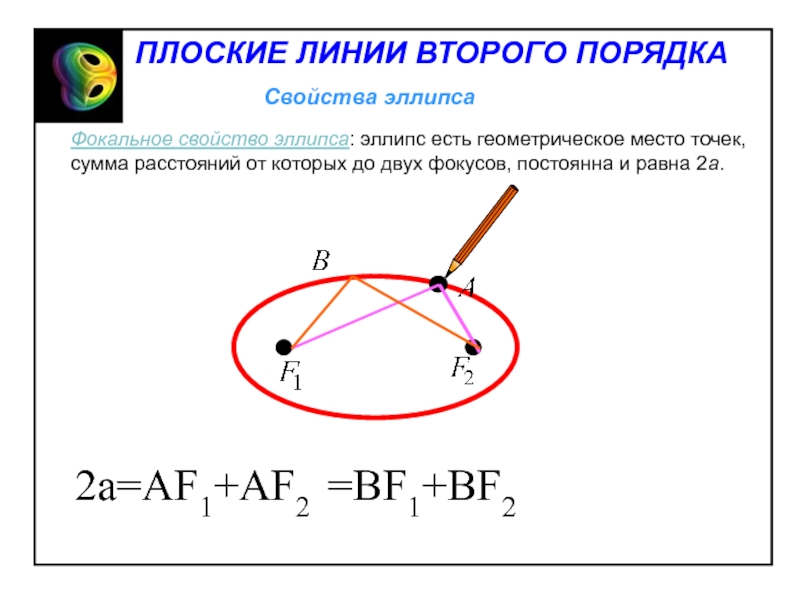
11. Свойства эллипсаФокальное свойство эллипса: эллипс есть геометрическое
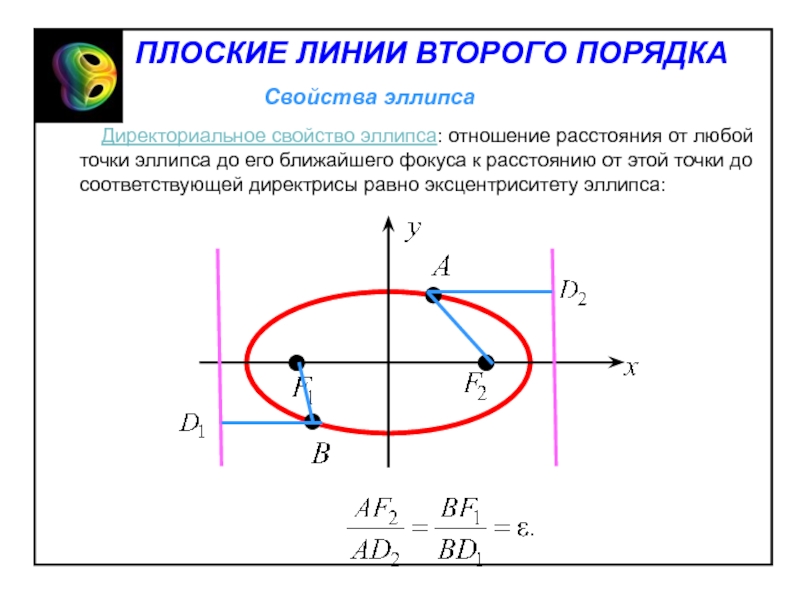
12. Директориальное свойство эллипса: отношение расстояния
13. Оптическое свойство эллипса:
14. b > a, то большая ось и
15. Слайд 15
16. Слайд 16
17. Слайд 17
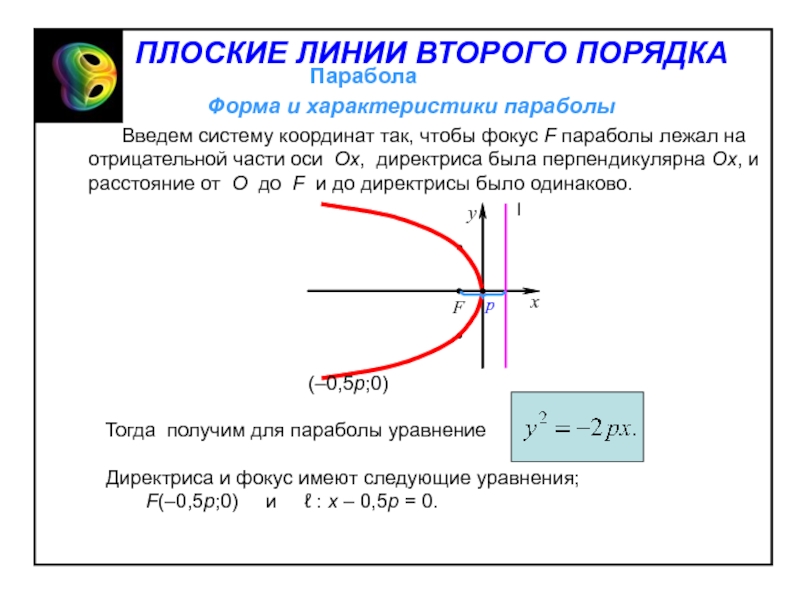
18. Выберем систему координат так,
19. Слайд 19
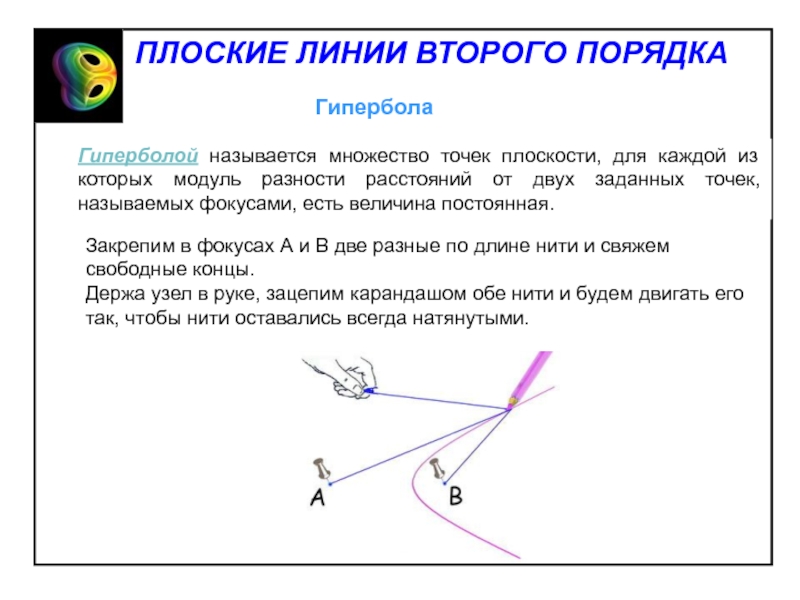
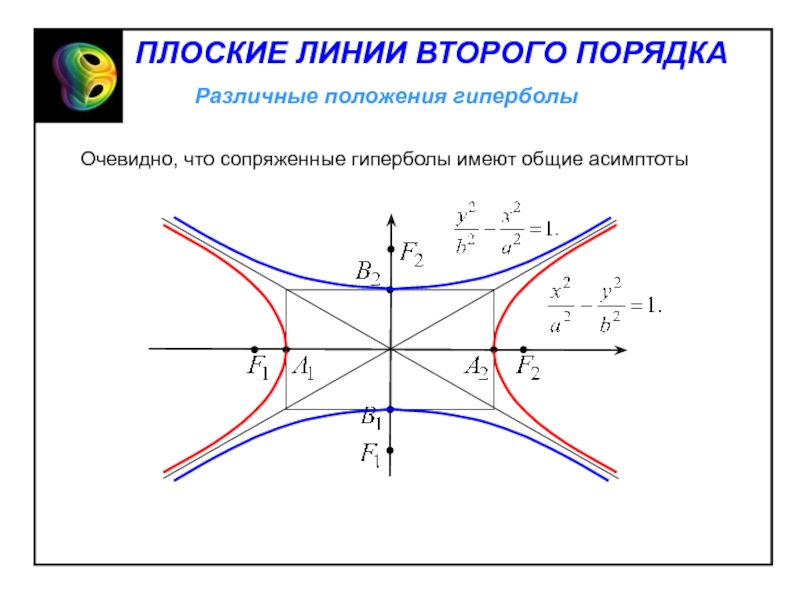
20. Гипербола симметрична относительно обеих координатных осей, т.к.
21. Слайд 21
22. Слайд 22
23. Слайд 23
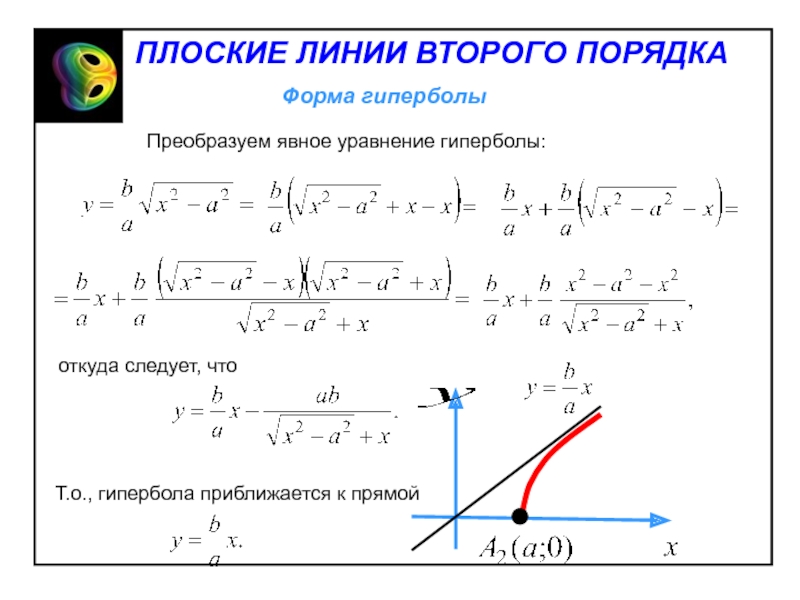
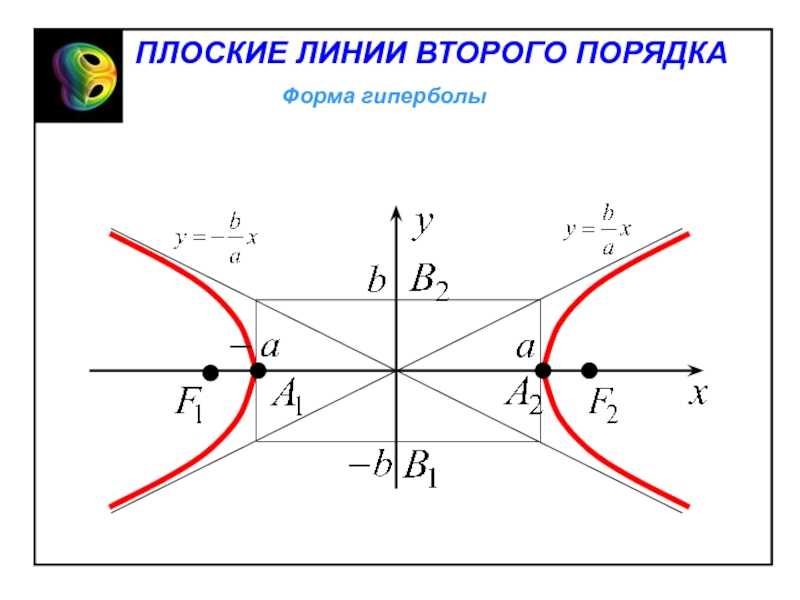
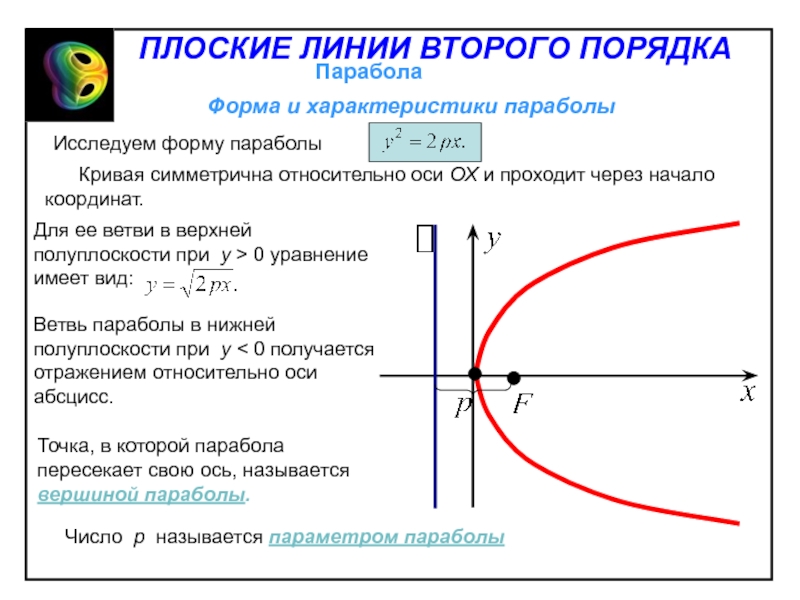
24. Форма гиперболыПЛОСКИЕ ЛИНИИ ВТОРОГО ПОРЯДКА
25. Слайд 25
26. Слайд 26
27. Слайд 27
28. Пример. Составить уравнение гиперболы при следующих условиях и найти недостающие параметры: b=3; c=4.
29. Слайд 29
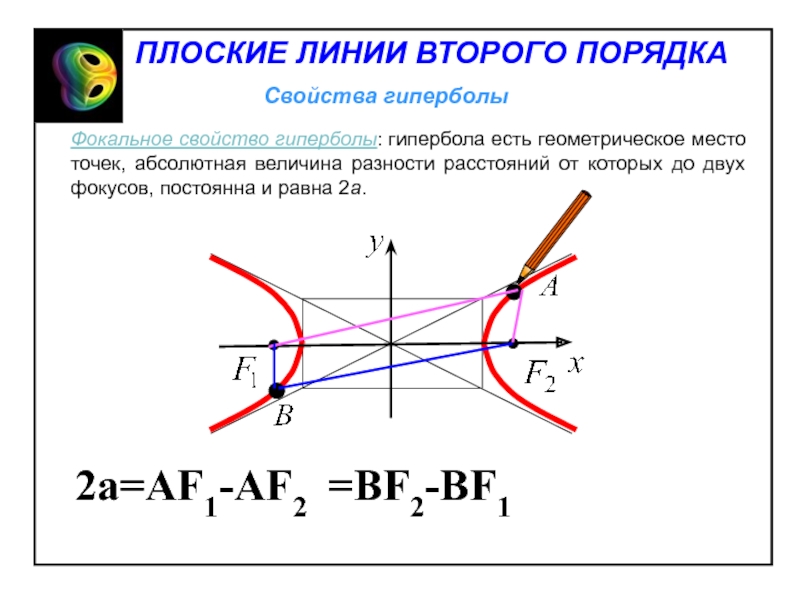
30. 2a=AF1-AF2=BF2-BF1
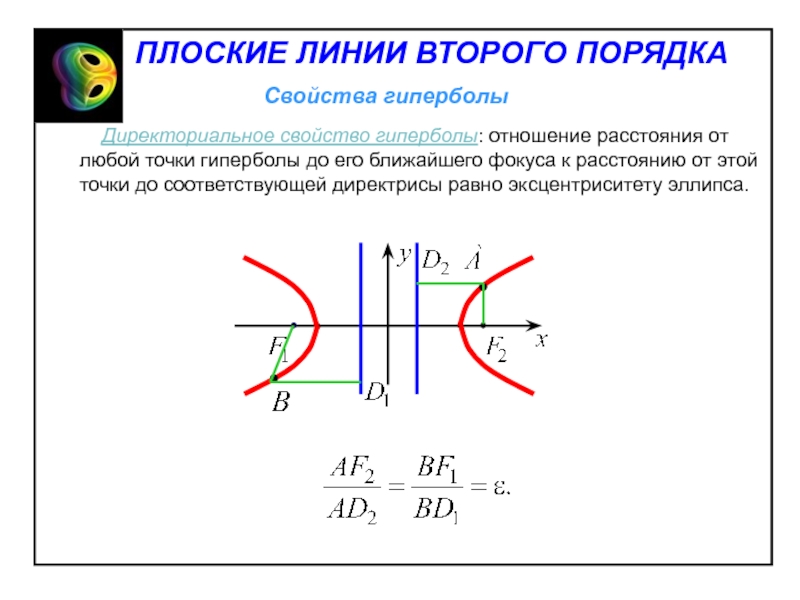
31. Директориальное свойство гиперболы: отношение расстояния
32. Слайд 32
33. Слайд 33
34. Слайд 34
35. Слайд 35
36. Если в уравнении гиперболы a=b, то гипербола
37. Слайд 37
38. Слайд 38
39. Слайд 39
40. Слайд 40
41. Слайд 41
42. Выберем систему координат
43. Пример. Составить уравнение параболы с вершиной в
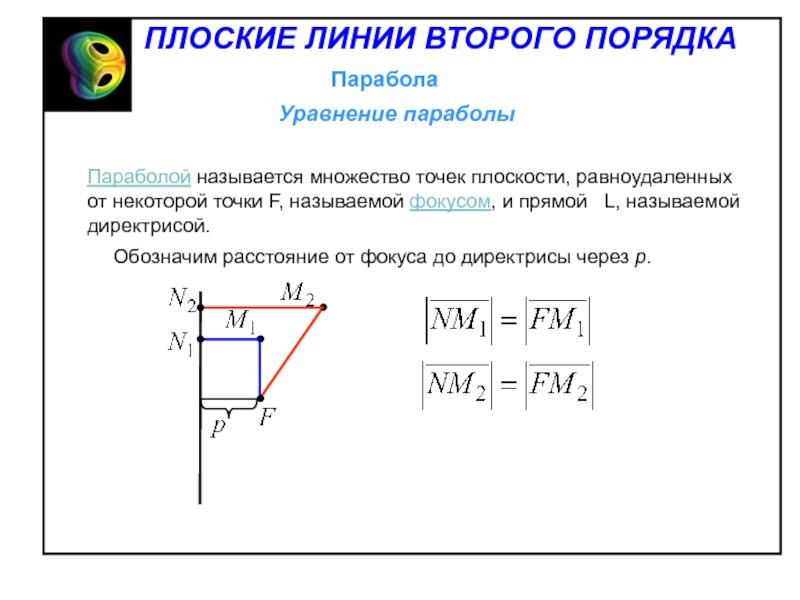
44. Директориальное свойство параболы: парабола есть геометрическое место
45. Это свойство
46. Слайд 46
47. Слайд 47
48. Слайд 48
49. Слайд 49
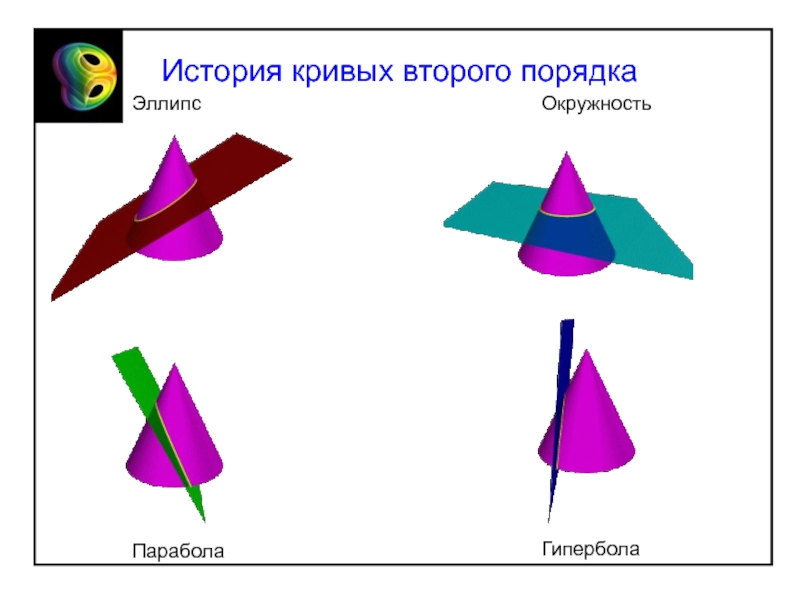
50. ЭллипсОкружностьПараболаГиперболаИстория кривых второго порядка
51. Скачать презентанцию

АНИМАЦИЯ ПОСТРОЕНИЯ ЭЛЛИПСА!!!

Главная
Разное
ПЛОСКИЕ ЛИНИИ ВТОРОГО ПОРЯДКА Окружность Окружностью называется геометрическое

Слайды и текст этой презентации

Слайд 2АНИМАЦИЯ ПОСТРОЕНИЯ ЭЛЛИПСА!!!

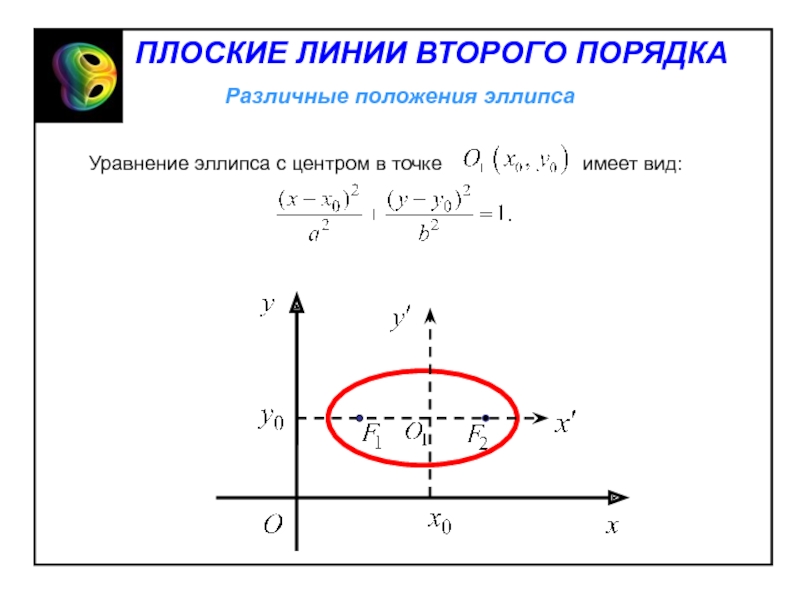
Слайд 4 Выберем систему координат так, чтобы фокусы лежали

на оси Ox симметрично относительно начала координат.

Слайд 6 Таким образом, эллипс симметричен относительно точки О 

центра эллипса.
Отрезки А1А2 = 2a и В1В2=

2b - большая и малая оси эллипса соответственно.

Таким образом, эллипс симметричен относительно точки О  центра эллипса. Отрезки А1А2 =

Слайд 7прямоугольника, образованного прямыми x= ± a и y= ± b.
эллипс

лежит внутри
Если M – произвольная точка эллипса, то

отрезки MF1 , MF2 и их длины r1, r2 называются фокальными радиусами точки M.

прямоугольника, образованного прямыми x= ± a и y= ± b.эллипс лежит внутри Если M – произвольная

Слайд 9 Определение. Две прямые, перпендикулярные большой оси

эллипса, расположенные симметрично относительно центра на расстоянии a/ε от

него, называются директрисами эллипса.

Определение. Две прямые, перпендикулярные большой оси эллипса, расположенные симметрично относительно центра на расстоянии

Слайд 11Свойства эллипса
Фокальное свойство эллипса: эллипс есть геометрическое место точек, сумма

расстояний от которых до двух фокусов, постоянна и равна 2a.
2a=AF1+AF2
=BF1+BF2
ПЛОСКИЕ

ЛИНИИ ВТОРОГО ПОРЯДКА

Свойства эллипсаФокальное свойство эллипса: эллипс есть геометрическое место точек, сумма расстояний от которых до двух фокусов, постоянна

Слайд 12 Директориальное свойство эллипса: отношение расстояния от любой точки

эллипса до его ближайшего фокуса к расстоянию от этой точки

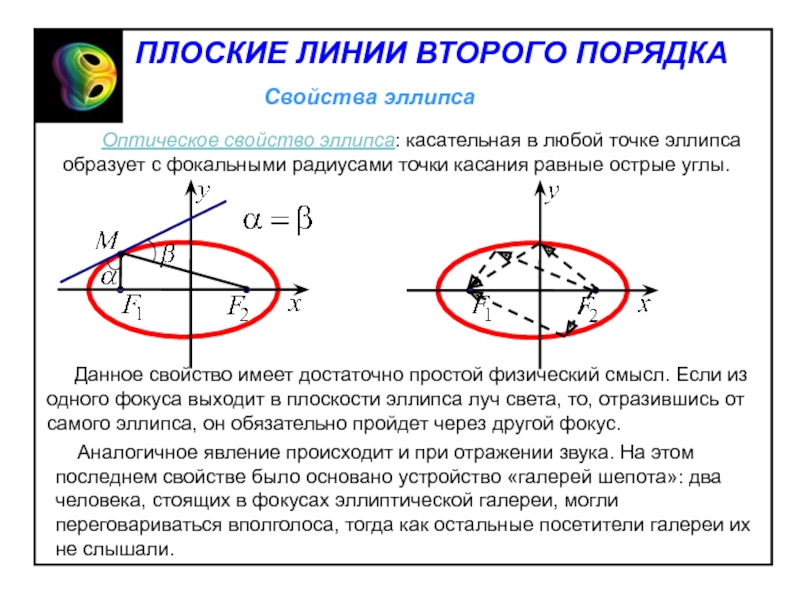
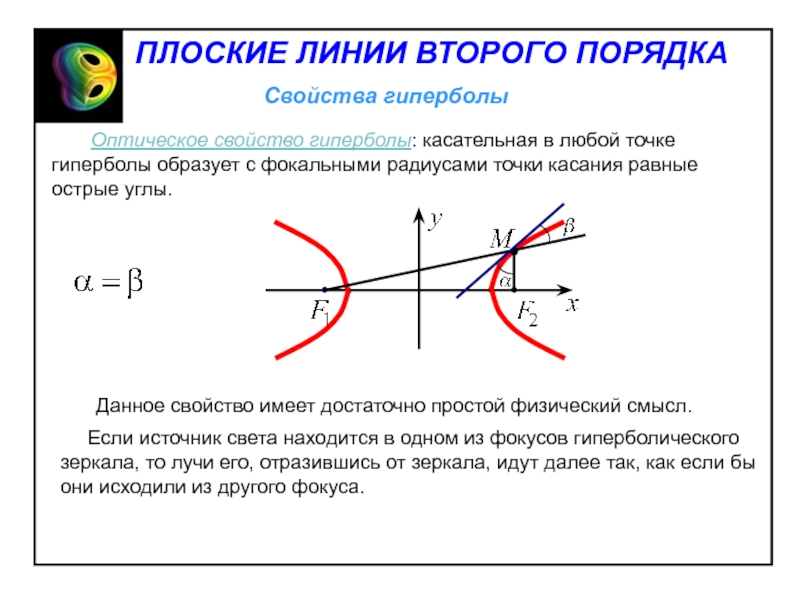
до соответствующей директрисы равно эксцентриситету эллипса:

Директориальное свойство эллипса: отношение расстояния от любой точки эллипса до его ближайшего фокуса к расстоянию

Слайд 13 Оптическое свойство эллипса: касательная в любой

точке эллипса образует с фокальными радиусами точки касания равные острые

углы.

Данное свойство имеет достаточно простой физический смысл. Если из одного фокуса выходит в плоскости эллипса луч света, то, отразившись от самого эллипса, он обязательно пройдет через другой фокус.

Аналогичное явление происходит и при отражении звука. На этом последнем свойстве было основано устройство «галерей шепота»: два человека, стоящих в фокусах эллиптической галереи, могли переговариваться вполголоса, тогда как остальные посетители галереи их не слышали.

Оптическое свойство эллипса: касательная в любой точке эллипса образует с фокальными радиусами точки

Слайд 14b > a, то большая ось и фокусы этого
Для этого

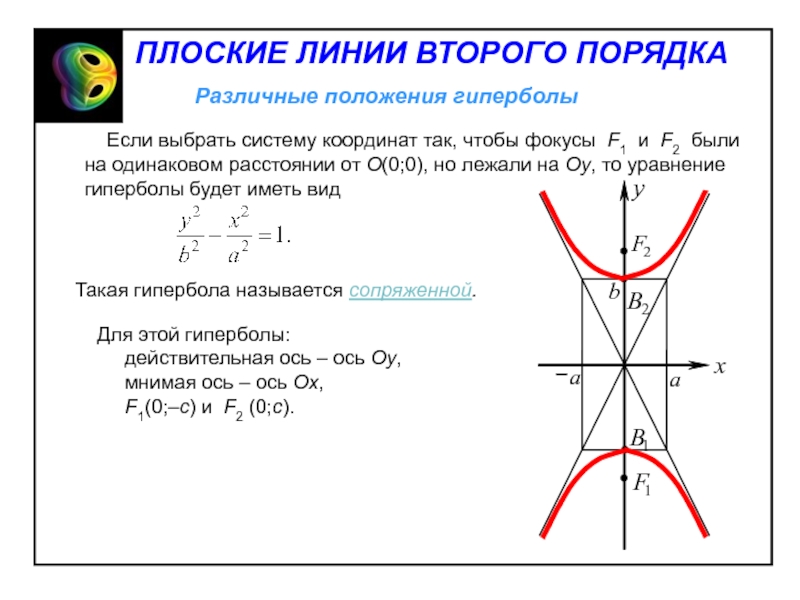
эллипса фокусы имеют координаты F1(0;–c) и F2(0;c) , где

Фокальные радиусы точки M(x;y) находятся по формулам

b > a, то большая ось и фокусы этогоДля этого эллипса фокусы имеют координаты F1(0;–c) и F2(0;c)

Слайд 15

Слайд 16

Слайд 17

Слайд 18 Выберем систему координат так, чтобы фокусы лежали

на оси Ox симметрично относительно начала координат.

Слайд 19

Слайд 20Гипербола симметрична относительно обеих координатных осей, т.к. его уравнение не

меняется при замене х на (- х) и у на

(- у).

Таким образом, гипербола симметрична относительно точки О  центра гиперболы.

Отрезки А1А2 и В1В2, а также их длины 2a и 2b – соответственно действительная и мнимая оси гиперболы.

Числа a и b – действительная и мнимая полуоси гиперболы.

Гипербола симметрична относительно обеих координатных осей, т.к. его уравнение не меняется при замене х на (- х)

Слайд 21

Слайд 22

Слайд 23

Слайд 24Форма гиперболы
ПЛОСКИЕ ЛИНИИ ВТОРОГО ПОРЯДКА

Слайд 25

Слайд 26

Слайд 27

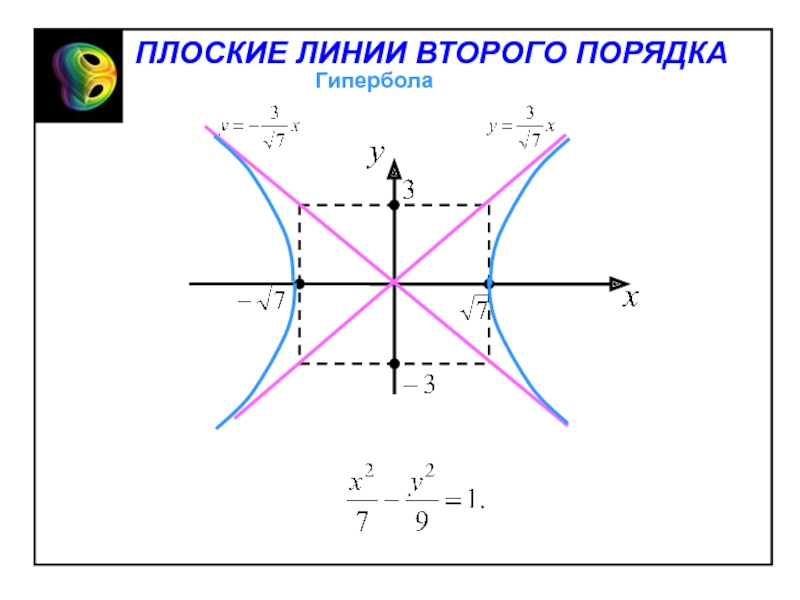
Слайд 28Пример. Составить уравнение гиперболы при следующих условиях и найти недостающие

параметры: b=3; c=4.

Слайд 29

Слайд 302a=AF1-AF2
=BF2-BF1

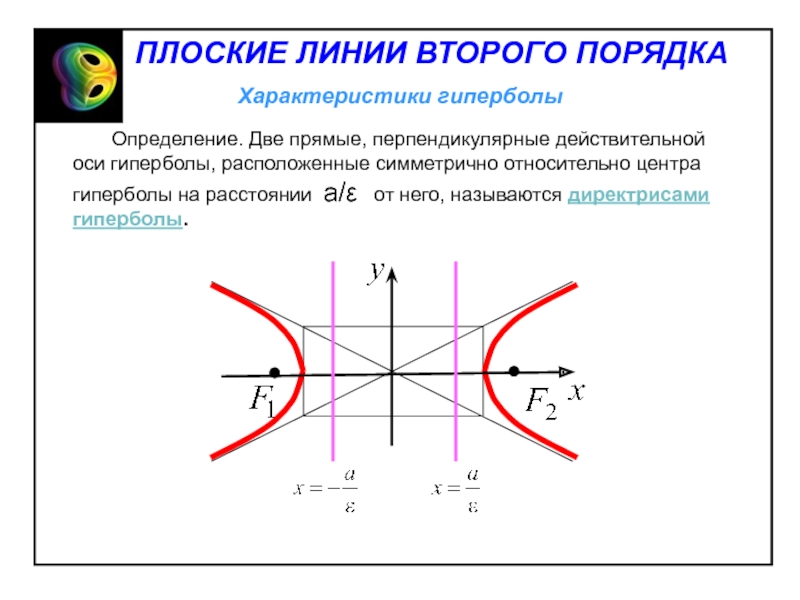
Слайд 31 Директориальное свойство гиперболы: отношение расстояния от любой точки

гиперболы до его ближайшего фокуса к расстоянию от этой точки

до соответствующей директрисы равно эксцентриситету эллипса.

Директориальное свойство гиперболы: отношение расстояния от любой точки гиперболы до его ближайшего фокуса к расстоянию

Слайд 32

Слайд 33

Слайд 34

Слайд 35

Слайд 36Если в уравнении гиперболы a=b, то гипербола называется равнобочной.

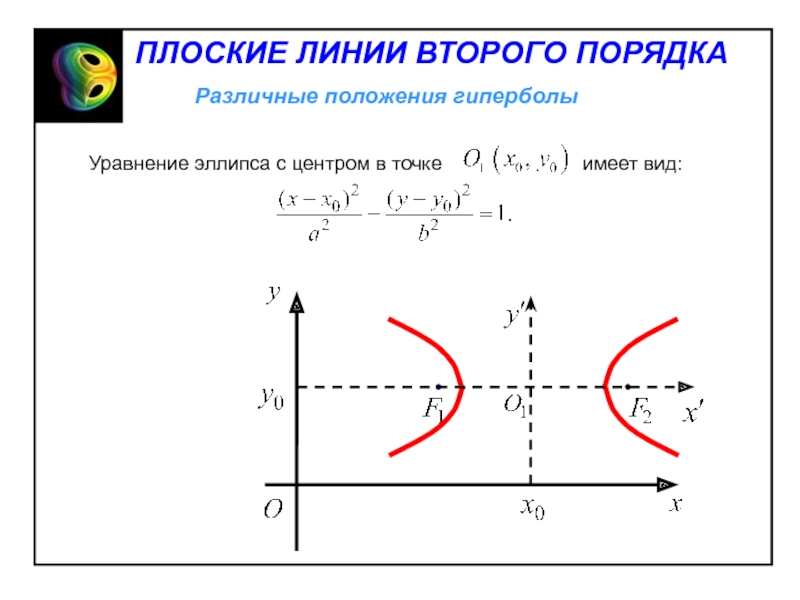
Для равнобочной гиперболы всегда можно выбрать систему координат так, чтобы

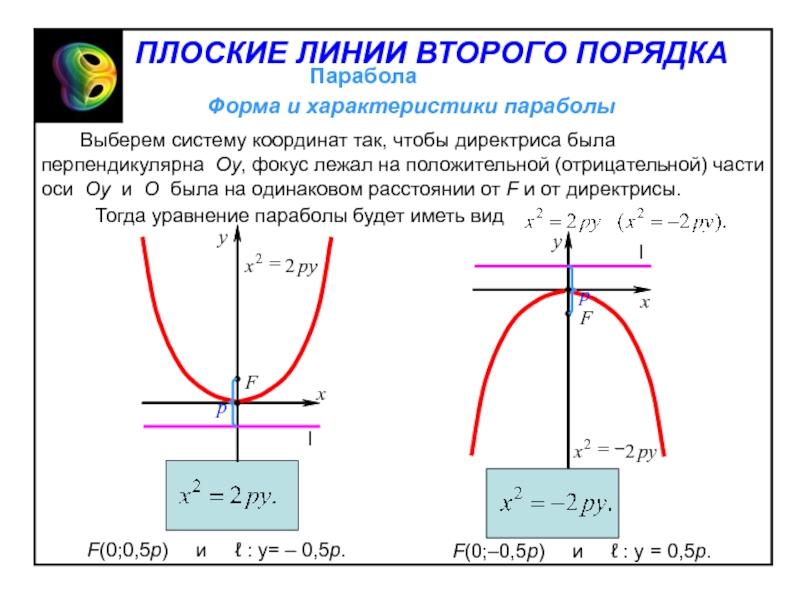
координатные оси совпали с асимптотами. Тогда уравнение гиперболы будет иметь вид

Если в уравнении гиперболы a=b, то гипербола называется равнобочной. Для равнобочной гиперболы всегда можно выбрать систему

Слайд 37

Слайд 38

Слайд 39

Слайд 40

Слайд 41

Слайд 42 Выберем систему координат так, чтобы директриса

была перпендикулярна Oy, фокус лежал на положительной (отрицательной) части оси

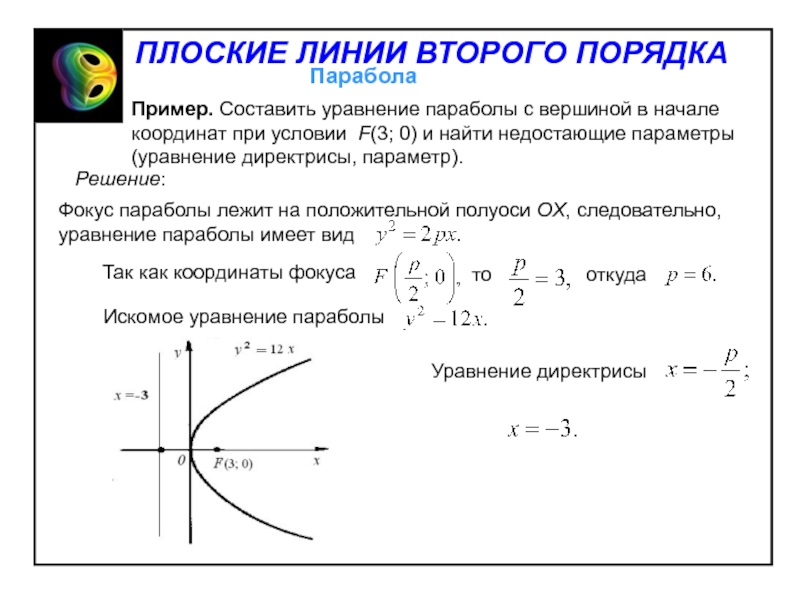
Oy и O была на одинаковом расстоянии от F и от директрисы.

Выберем систему координат так, чтобы директриса была перпендикулярна Oy, фокус лежал на положительной

Слайд 43Пример. Составить уравнение параболы с вершиной в начале координат при

условии F(3; 0) и найти недостающие параметры (уравнение директрисы, параметр).
Решение:

Фокус параболы лежит на положительной полуоси OX, следовательно, уравнение параболы имеет вид

Так как координаты фокуса

то

откуда

Искомое уравнение параболы

Уравнение директрисы

Пример. Составить уравнение параболы с вершиной в начале координат при условии F(3; 0) и найти недостающие параметры

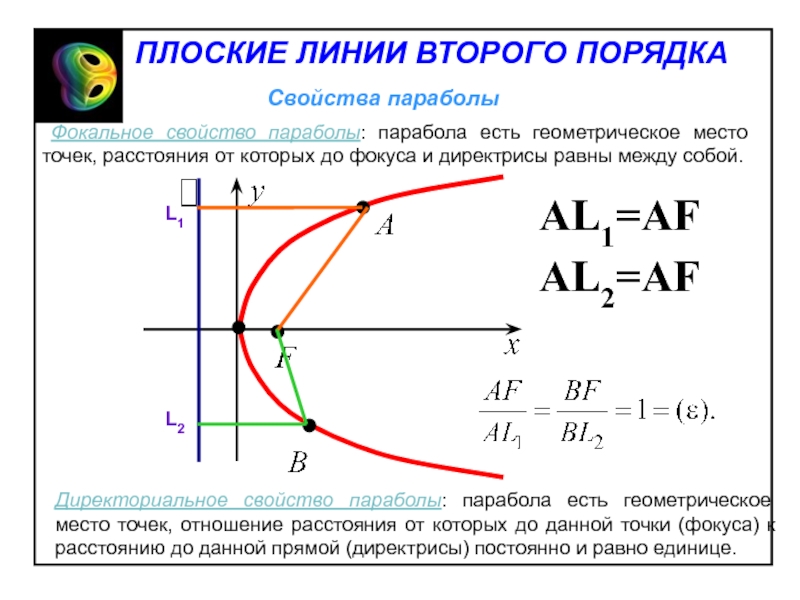
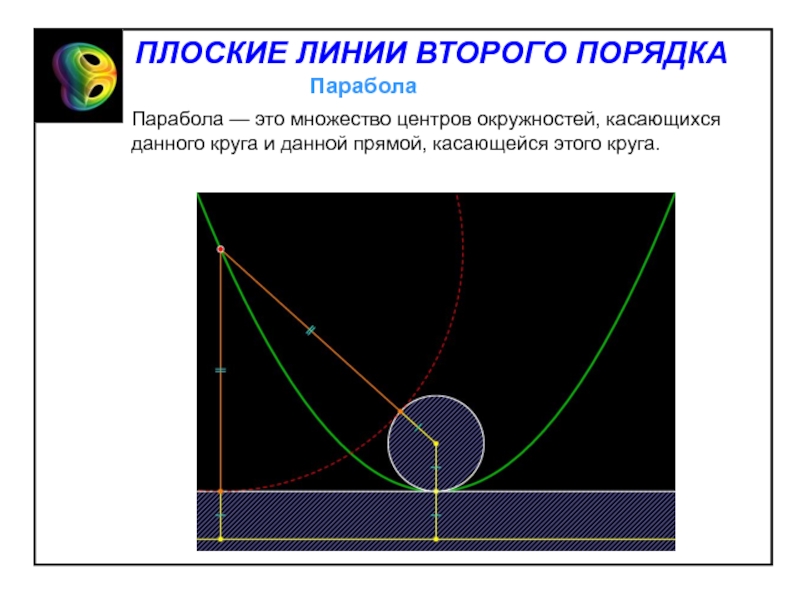
Слайд 44Директориальное свойство параболы: парабола есть геометрическое место точек, отношение расстояния

от которых до данной точки (фокуса) к расстоянию до данной

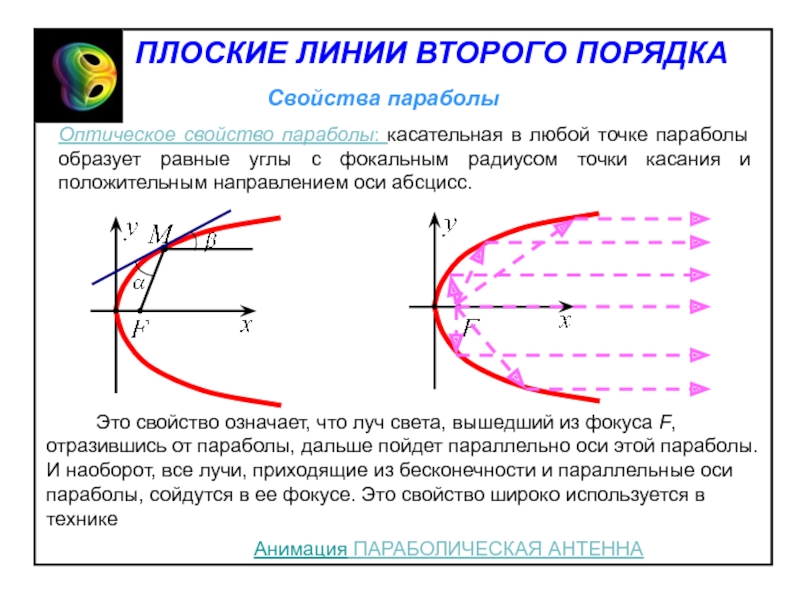
прямой (директрисы) постоянно и равно единице.

Директориальное свойство параболы: парабола есть геометрическое место точек, отношение расстояния от которых до данной точки (фокуса) к

Слайд 45 Это свойство означает, что луч

света, вышедший из фокуса F, отразившись от параболы, дальше пойдет

параллельно оси этой параболы. И наоборот, все лучи, приходящие из бесконечности и параллельные оси параболы, сойдутся в ее фокусе. Это свойство широко используется в технике

Анимация ПАРАБОЛИЧЕСКАЯ АНТЕННА