Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Показатели вариации и способы их вычисления
Содержание
- 1. Показатели вариации и способы их вычисления
- 2. Размах (амплитуда) колебанийРазмах (амплитуда) колебаний (размах вариации) - это разность между наименьшей и наибольшей вариантой.2
- 3. Квартильное отклонениеКвартильное отклонение применяется вместо размаха вариа-ции,
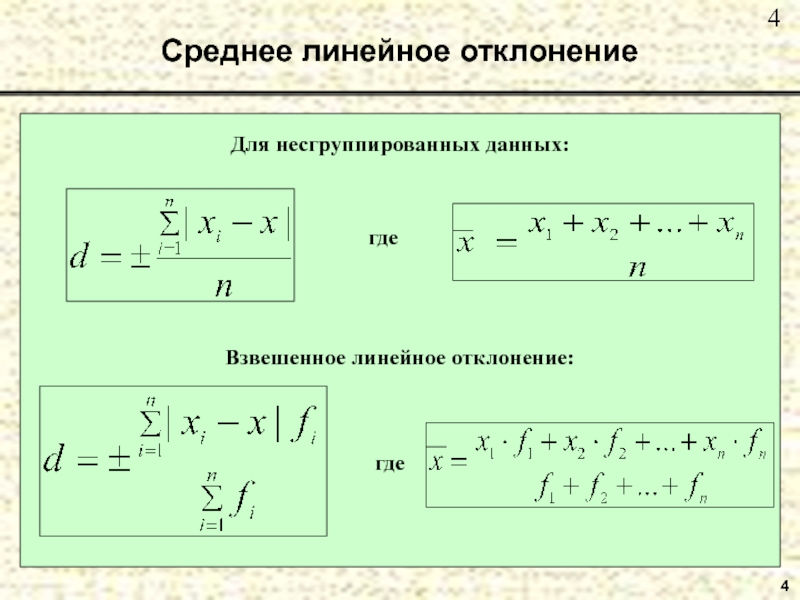
- 4. Среднее линейное отклонение4Для несгруппированных данных:Взвешенное линейное отклонение:
- 5. Среднее квадратическое отклонение5Простое квадратическое отклонение:
- 6. Среднее квадратическое отклонение6Пример. Имеются следующие данные о
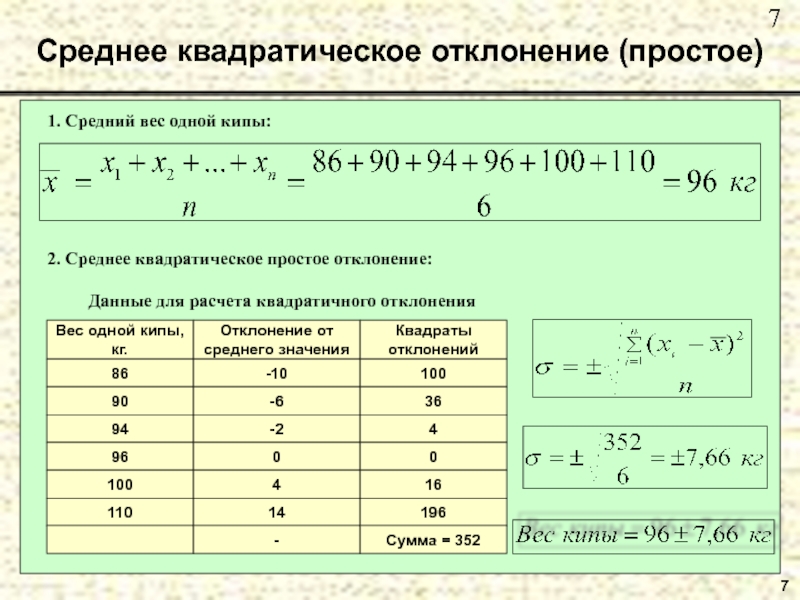
- 7. Среднее квадратическое отклонение (простое)7
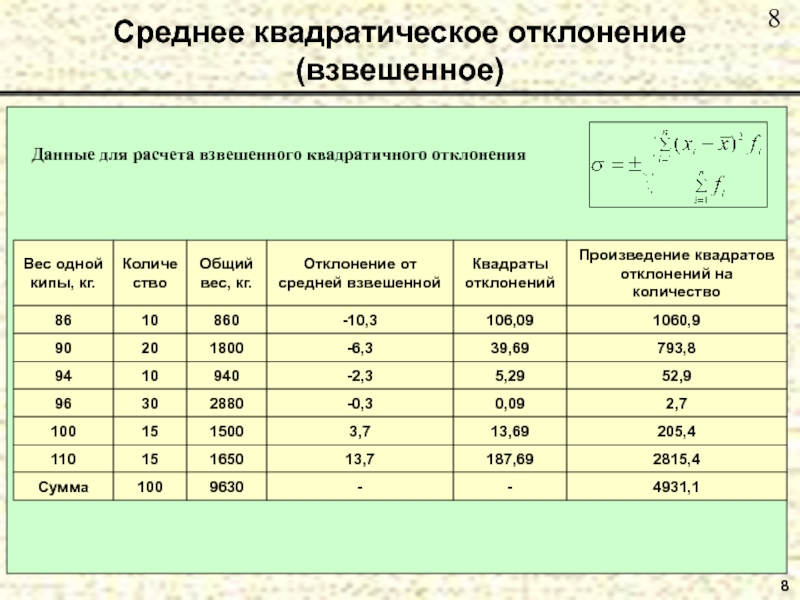
- 8. Среднее квадратическое отклонение (взвешенное)8
- 9. Среднее квадратическое отклонение (взвешенное)9
- 10. Относительные показатели вариации10Коэффициент осцилляции:
- 11. 11Коэффициент вариацииКоэффициент вариации представляет собой отношение сред-него
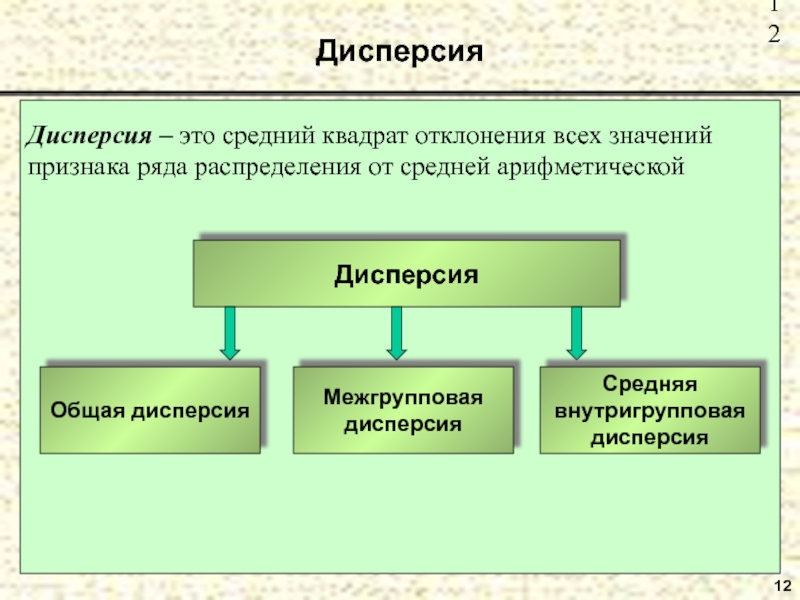
- 12. Дисперсия12Дисперсия – это средний квадрат отклонения всех значений признака ряда распределения от средней арифметическойДисперсия
- 13. Общая дисперсия13Общая дисперсия характеризует вариацию признака под
- 14. Межгрупповая дисперсия14Межгрупповая дисперсия отражает те различия в
- 15. Средняя внутригрупповая дисперсия15Средняя внутригрупповая дисперсия характеризует случайную
- 16. Правило сложения дисперсий 16Величина общей дисперсии равна
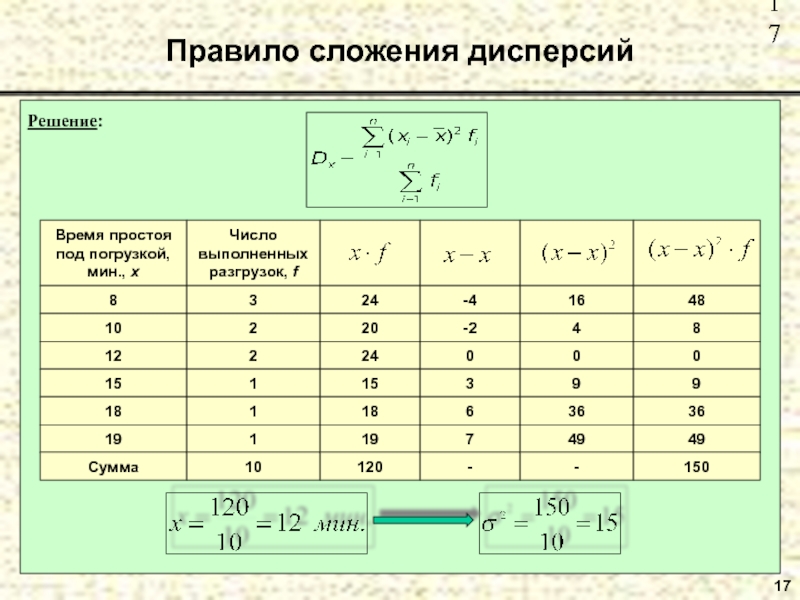
- 17. Правило сложения дисперсий17Решение:
- 18. Правило сложения дисперсий18Расчет внутригрупповой дисперсии по первой группе (число грузчиков, участвующих в разгрузке – 3)
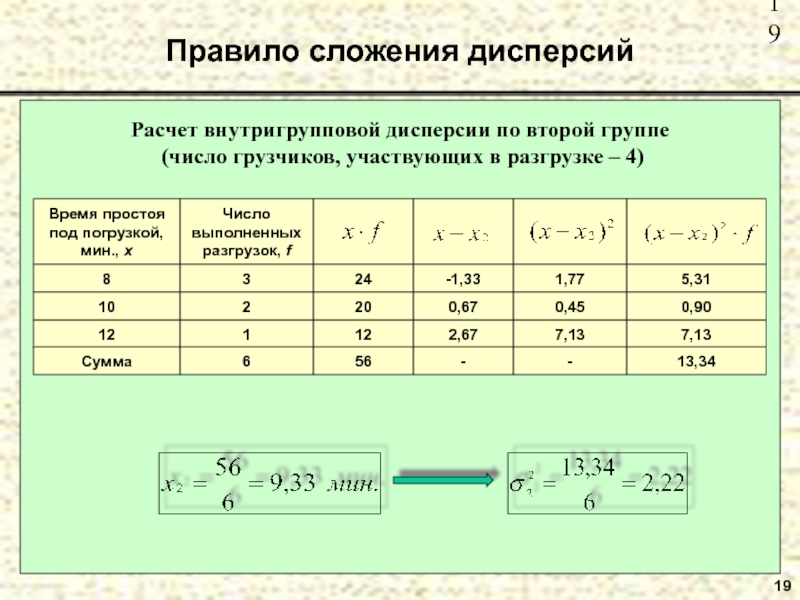
- 19. Правило сложения дисперсий19Расчет внутригрупповой дисперсии по второй группе (число грузчиков, участвующих в разгрузке – 4)
- 20. Правило сложения дисперсий20Средняя внутригрупповая дисперсия:
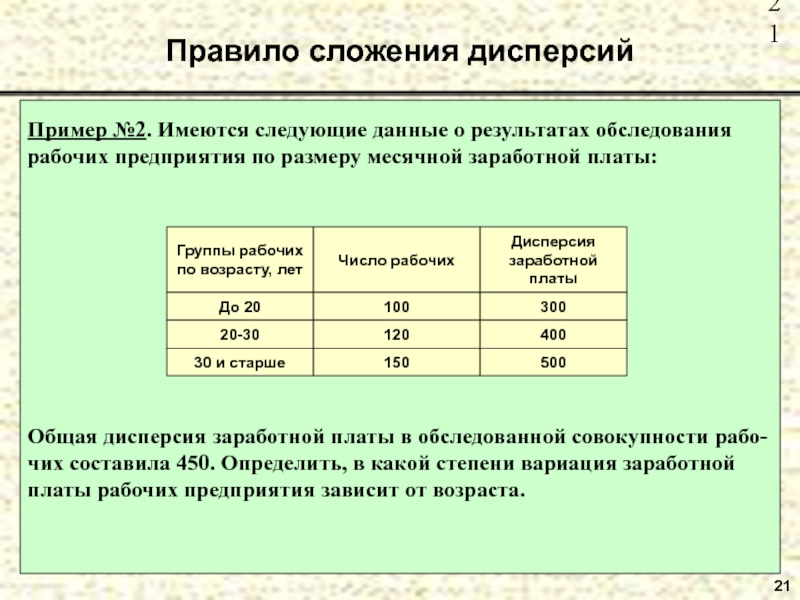
- 21. Правило сложения дисперсий21Пример №2. Имеются следующие данные
- 22. Правило сложения дисперсий22Соотношение дисперсий:Решение.Средняя внутригрупповая дисперсия характеризует
- 23. Преобразование формулы для расчёта общей дисперсии23Формула для расчёта общей дисперсии может быть преобразована:
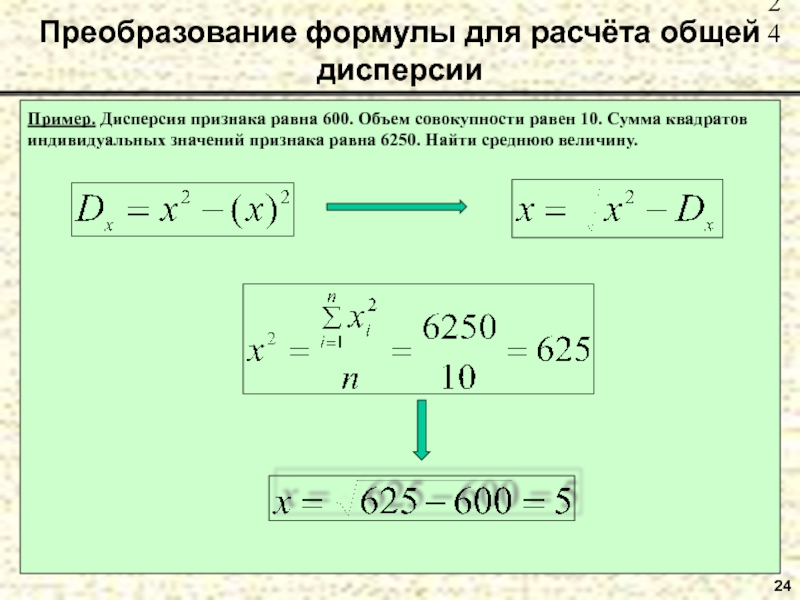
- 24. Преобразование формулы для расчёта общей дисперсии24Пример. Дисперсия
- 25. Вариации альтернативного признака25Альтернативный признак – качественный признак,
- 26. Пример. Удельный вес основных рабочих в трех
- 27. Скачать презентанцию
Размах (амплитуда) колебанийРазмах (амплитуда) колебаний (размах вариации) - это разность между наименьшей и наибольшей вариантой.2
Слайды и текст этой презентации
Слайд 1Автор: Равичев Л.В.
РХТУ им. Д.И.Менделеева
Кафедра управления технологическими инновациями
Москва - 2013
СТАТИСТИКА.
Описательная
статистика.
Слайд 2Размах (амплитуда) колебаний
Размах (амплитуда) колебаний (размах вариации) - это разность
между наименьшей и наибольшей вариантой.
2
Слайд 3Квартильное отклонение
Квартильное отклонение применяется вместо размаха вариа-ции, чтобы избежать недостатков,
связанных с использованием крайних значений.
3
где Q1 и Q3 – соответственно
третья и первая квартили распреде-ления.Слайд 6
Среднее квадратическое отклонение
6
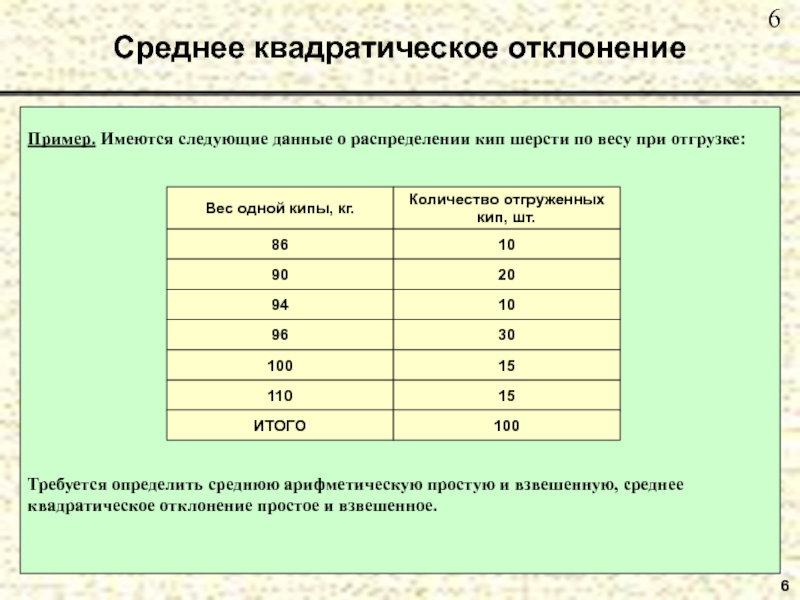
Пример. Имеются следующие данные о распределении кип шерсти
по весу при отгрузке:
Требуется определить среднюю арифметическую простую и взвешенную,
среднее квадратическое отклонение простое и взвешенное.Слайд 1111
Коэффициент вариации
Коэффициент вариации представляет собой отношение сред-него квадратического отклонения к
средней арифметической и показывает величину отклонения (в процентах) от средней
вели-чины.Слайд 12Дисперсия
12
Дисперсия – это средний квадрат отклонения всех значений признака ряда
распределения от средней арифметической
Дисперсия
Слайд 13Общая дисперсия
13
Общая дисперсия характеризует вариацию признака под влия-нием всех факторов,
формирующих уровень признака у единиц данной совокупности.
Слайд 14Межгрупповая дисперсия
14
Межгрупповая дисперсия отражает те различия в величине изучаемого признака,
которые возникают под влиянием факто-ра, положенного в основу группировки.
Слайд 15Средняя внутригрупповая дисперсия
15
Средняя внутригрупповая дисперсия характеризует случайную вариацию, возникающую под
влиянием других, неучтенных факторов, и не зависит от условия, положенного
в основу груп-пировки.Слайд 16Правило сложения дисперсий
16
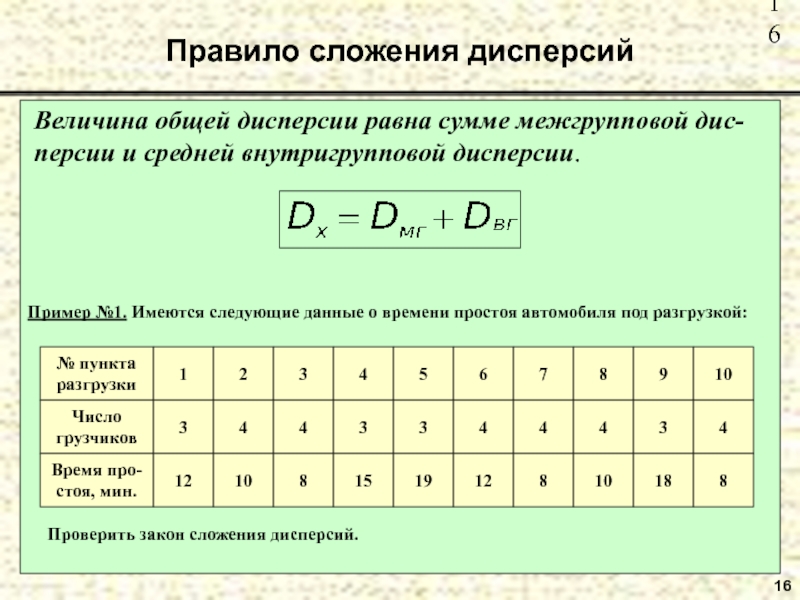
Величина общей дисперсии равна сумме межгрупповой дис-персии
и средней внутригрупповой дисперсии.
Пример №1. Имеются следующие данные о времени
простоя автомобиля под разгрузкой:Проверить закон сложения дисперсий.
Слайд 18Правило сложения дисперсий
18
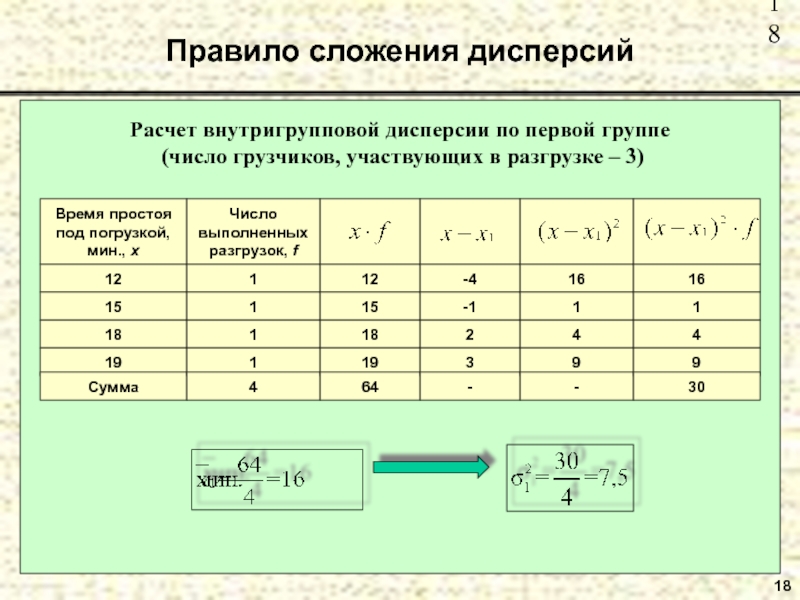
Расчет внутригрупповой дисперсии по первой группе
(число грузчиков,
участвующих в разгрузке – 3)
Слайд 19
Правило сложения дисперсий
19
Расчет внутригрупповой дисперсии по второй группе
(число грузчиков,
участвующих в разгрузке – 4)
Слайд 21
Правило сложения дисперсий
21
Пример №2. Имеются следующие данные о результатах обследования
рабочих предприятия по размеру месячной заработной платы:
Общая дисперсия заработной платы
в обследованной совокупности рабо-чих составила 450. Определить, в какой степени вариация заработной платы рабочих предприятия зависит от возраста.Слайд 22
Правило сложения дисперсий
22
Соотношение дисперсий:
Решение.
Средняя внутригрупповая дисперсия характеризует случайную вариацию под
влиянием неучтенных факторов:
Межгрупповая дисперсия отражает систематическую вариацию под влиянием фактора,
положенного в основу группировки (возраста рабо-чих):Слайд 23
Преобразование формулы для расчёта общей дисперсии
23
Формула для расчёта общей дисперсии
может быть преобразована:
Слайд 24
Преобразование формулы для расчёта общей дисперсии
24
Пример. Дисперсия признака равна 600.
Объем совокупности равен 10. Сумма квадратов индивидуальных значений признака равна
6250. Найти среднюю величину.Слайд 25
Вариации альтернативного признака
25
Альтернативный признак – качественный признак, имеющий две взаимо-исключающие
разновидности. Альтернативный признак принимает всего два значения: 1 – наличие
признака; 0 – отсутствие признака.Слайд 26Пример. Удельный вес основных рабочих в трех цехах предприятия составил:
80, 75 и 90% общей численности рабочих. Определить дисперсию и
среднее квад-ратическое отклонение доли основных рабочих по предприятию в целом, если численность всех рабочих трех цехов составила соответственно 100, 200 и 150 человек.Вариации альтернативного признака
26