Слайд 1
Основные положения
сопротивления материалов
Все части
машин под действием нагрузок деформируются, т.е. изменяют свою форму и
размеры, в некоторых случаях происходит разрушение деталей машин.
Сопротивление материалов наука о прочности и деформируемости материалов и элементов машин.
ВИДЫ НАГРУЗОК
На деталь машины в процессе эксплуатации действуют внешние и внутренние силы.
Внешние силы - активные силы и реакции внешних связей (опор).
Слайд 2
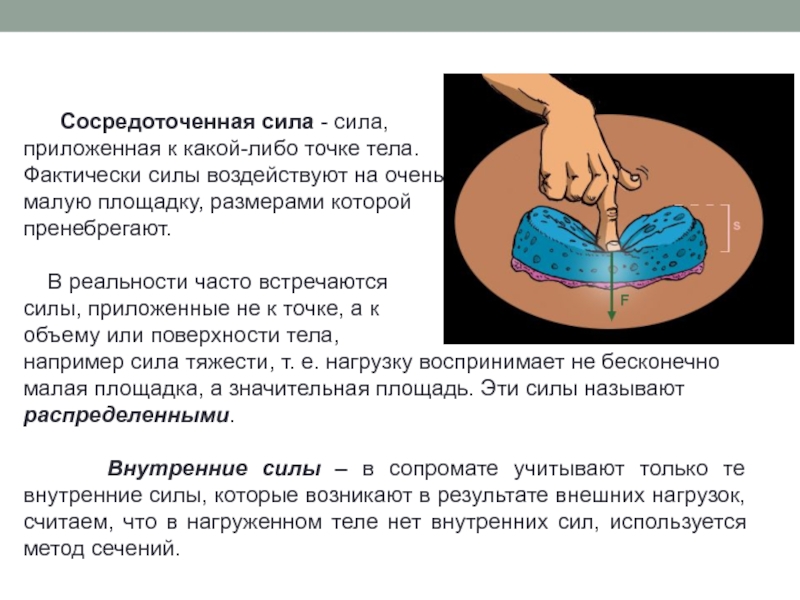
Сосредоточенная сила - сила,
приложенная к какой-либо точке тела.
Фактически силы воздействуют на очень
малую площадку, размерами которой
пренебрегают.
В реальности часто встречаются
силы, приложенные не к точке, а к
объему или поверхности тела,
например сила тяжести, т. е. нагрузку воспринимает не бесконечно
малая площадка, а значительная площадь. Эти силы называют распределенными.
Внутренние силы – в сопромате учитывают только те внутренние силы, которые возникают в результате внешних нагрузок, считаем, что в нагруженном теле нет внутренних сил, используется метод сечений.
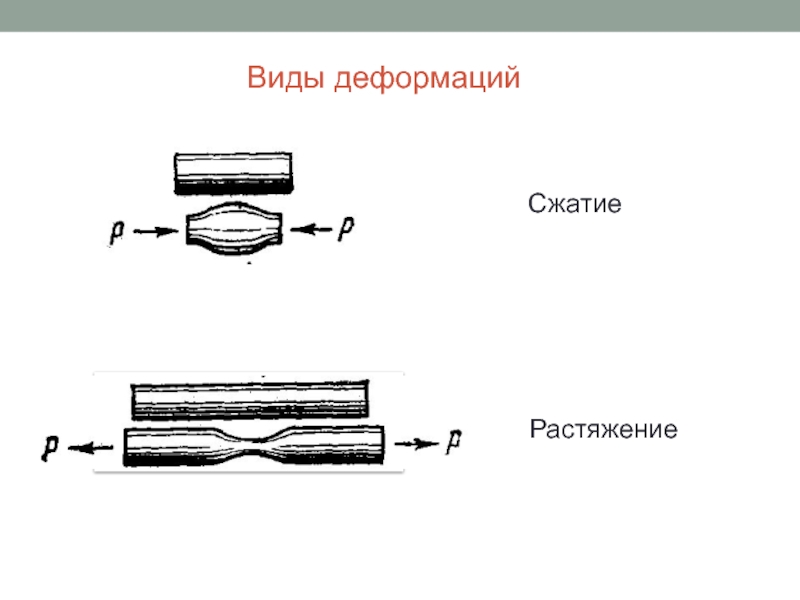
Слайд 3Виды деформаций
Сжатие
Растяжение
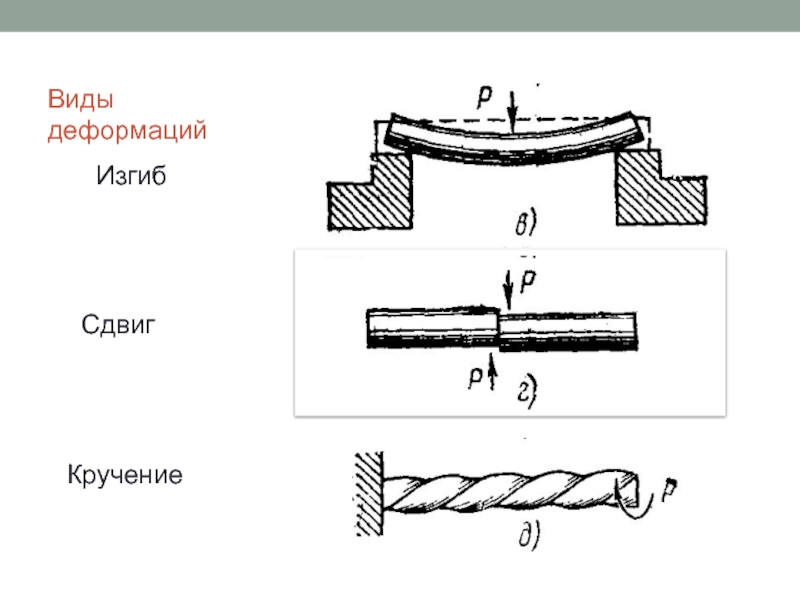
Слайд 4Виды деформаций
Изгиб
Сдвиг
Кручение
Слайд 5 Детали машин подвергаются действию совместных
различных нагрузок.
Вал-шестерня испытывает одновременно
изгиб и кручение.
Слайд 6 Для расчетов элементов конструкции на прочность необходимо
знать внутренние силы, возникающие в результате приложения внешних сил в
разных точках и частях конструкции.
Способы определения этих внутренних сил с помощью науки сопротивление материалов включают такой прием, как метод сечений.
Метод сечений. Напряжения
Метод сечений заключается в том, что тело мысленно рассекается плоскостью на две части, любая из которых отбрасывается и взамен ее к сечению оставшейся части прикладываются внутренние силы, действовавшие на нее до разреза
Слайд 7 Тело мысленно рассекается плоскостью на две части, и
взамен ее к сечению оставшейся части прикладываются внутренние силы, действовавшие
на нее до разреза
Брус состоит из двух участков.
Методом сечений определены продольные внутренние силы N1 и N2 на этих участках.
Уравнение равновесия :
∑ Z = 0, 2F – F – N1 = 0,
N1 = 2F – F = F.
В сечении 2-2 продольная сила N2 = 2F.
Слайд 8 При растяжении и сжатии в сечениях вала возникают
нормальные напряжения,
равномерно распределенные по сечению.
Напряжения
определены по формуле:
σ = N / А,
где N – продольная сила,
А – площадь поперечного сечения вала.
При растяжении и сжатии форма сечения
вала на величину напряжений не влияет.
Наглядно изобразить распределение
продольных сил и нормальных напряжений вдоль оси вала можно с помощью графиков, которые называются эпюрами. При этом на эпюрах при построении учитывают знаки (векторные значения) продольных сил и напряжений.
Если продольная сила направлена
от сечения, то брус растянут. Растяжение считают положительной деформацией (рис. а).
Если продольная сила направлена к сечению, то брус сжат. Сжатие считают отрицательной деформацией (рис. б).
Слайд 10Задача
Определить внутренние силы внутри каждого участка.
∑ F = 0;
- 3 F + N1 = 0; N1 =
3F.
Продольная сила положительна, участок 1 растянут.
∑ F = 0; - 3 F + 2 F + N2 = 0; N2 = F.
Продольная сила положительна, участок 2 растянут.
∑ F = 0; - 3 F + 2 F + 5F – N3 = 0; N3 = 4F.
Продольная сила отрицательна, участок 3 сжат.
Строим эпюру продольной силы.
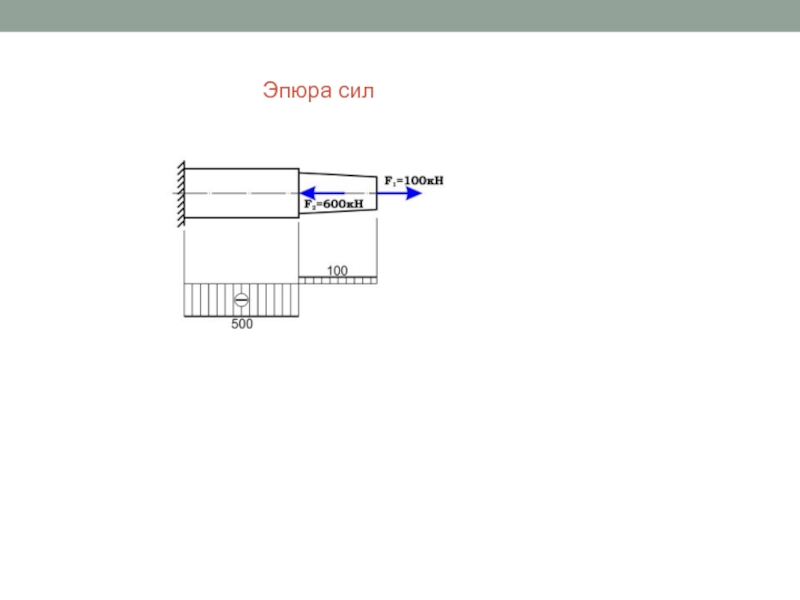
Слайд 11ПОСТРОИТЬ ЭПЮРУ СИЛ
Правило контроля:
в месте приложения внешней силы на эпюре должен быть скачок
на величину приложенной силы