Слайд 1Прикладная химия
Уравнение материального баланса.
Основы гидродинамики
Слайд 2Материальный баланс реактора
Материальный баланс – это равенство прихода и расхода
вещества в реакторе или в процессе. Теоретической основой составления материальных
балансов является закон сохранения материи М.И. Ломоносова.
Составим материальный баланс реактора, в котором протекает простая необратимая реакция
А → С
Масса реагента, поступающего в реактор, в единицу времени, равно массе реагента А, расходуемому в реакторе в единицу времени:
mА приход = mА расход
Слайд 3Уравнение материального баланса реактора
Реагент А расходуется на химическую реакцию(mА хим.р.),
часть реагента выходит из реактора(mА сток), часть – остается в
реакционном объеме в неизменном виде (накапливается, mА накопл):
mА расход = mА хим.р. + mА сток + mА накопл.
Так как mА расход = mА приход, то:
mА приход = mА хим.р. + mА сток + mА накопл.
mА приход - mА сток = mА хим.р. + mА накопл.
Обозначим mА приход - mА сток = mА конвек. – масса реагента А, переносимого за счет конвекции (потоком реакционной массы).Тогда
mА накопл. = mА конвек. - mА хим.р.
Масса реагента А, остающееся неизменным в реакционном потоке, равно разнице между массой вещества А, переносимым конвективным потоком, и массой вещества А, израсходованным на химическую реакцию. Это есть уравнение материального баланса в общем виде.
Слайд 4Уравнение материального баланса реактора
Когда концентрация реагента непостоянна в различных точках
объема реактора или во времени, нельзя составлять материальный баланс в
общем виде, для всего объема реактора. В этом случае составляют материальный баланс для элементарного объема реактора.
Слайд 5Уравнение материального баланса для элементарного объема реактора
Основой этого материального баланса
является уравнение конвективного переноса:
где СА – концентрация реагента А в реакционной
смеси;
x,y,z – пространственные координаты;
Wx, Wy, Wz – составляющие скорости потока;
D – коэффициент диффузии;
rA – скорость химической реакции.
Слайд 6Уравнение материального баланса для элементарного объема реактора
Первый член уравнения
характеризует изменение концентрации реагента А во времени в элементарном объеме
и соответствует mА накопл. в общем уравнении материального баланса.
Второй и третий члены:
характеризуют суммарный перенос вещества в движущейся среде путем конвекции и диффузии; в общем уравнение материального баланса им соответствует член mА конвек..
Член rA показывает изменение концентрации реагента А в элементарном объеме за счет химической реакции. Ему соответствует член m А хим.р. в общем уравнении материального баланса.
Слайд 7Основы гидродинамики
Решение этих уравнений является сложной задачей и зачастую оно
невозможно без знания законов гидродинамики, так как реагенты чаще всего
поступают в реактор в газовой или жидкой фазе.
Гидродинамика математически и качественно описывает процессы взаимодействия жидкости (газа) с поверхностями, находящимися в покое и движении.
Движение жидкости коренным образом отличается от перемещения твердых тел. При движении жидкость не сохраняет расстояние между ее частями (частицами). В общем случае при движении жидкости учитывают массовые силы и силы трения (вязкость) жидкости.
Слайд 8Основы гидродинамики
Перемещающуюся жидкость характеризуют при помощи двух параметров:
скорости течения
(U)
и гидродинамического давления (p).
Основной задачей гидродинамики является их
определение при известной системе действующих внешних сил.
Для решения данной задачи существенным является тип движения жидкости:
установившееся движение
неустановившееся движение жидкости.
Слайд 9Движение жидкости
В состоянии равновесия жидкости (газа) давление p изменяется в
зависимости от плотности (ρ) и температуры (T) и однозначно определено
ими:
p=f(ρ, T)
Если движение жидкости является установившимся, то p и U являются функциями координат и не зависят от времени:
p=f(x,y,z) и U=f(x,y,z)
При неустановившемся движении жидкости скорость и давление являются функциями от координат и времени:
p=f(x,y,z,t) и U=f(x,y,z,t)
Слайд 10Движение жидкости
Движение жидкости называют течением, совокупность частиц перемещающейся жидкости –
это поток. Так же потоком жидкости считают перемещающуюся массу жидкости,
которая полностью или частично ограничена поверхностями.
Эти поверхности могут образовываться самой жидкостью на фазовой границе или быть твердыми. Границы потоков – это стенки трубы, канала, поверхность, которую жидкость обтекает, открытая поверхность жидкости.
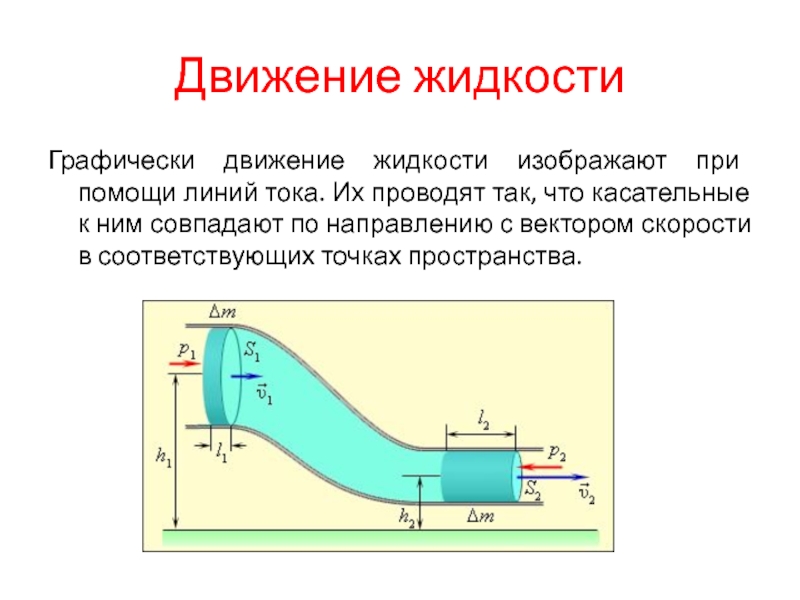
Слайд 11Движение жидкости
Графически движение жидкости изображают при помощи линий тока. Их
проводят так, что касательные к ним совпадают по направлению с
вектором скорости в соответствующих точках пространства.
Слайд 12Идеальные и несжимаемые жидкости
Под идеальным газом/раствором/жидкостью в химии подразумевается объекты,
составляющие части которого ни химически ни физически не взаимодействуют друг
с другом.
Применительно к гидродинамике отсутствие взаимодействия между частицами приводит к отсутствию сил трения, которые должны порождать вязкость жидкости.
То есть «идеальная жидкость» в гидродинамике – это жидкость без вязкости.
Кроме того, малая сжимаемость жидкости дает возможность в некоторых случаях полностью пренебречь изменением ее объема. При этом говорят о несжимаемой жидкости.