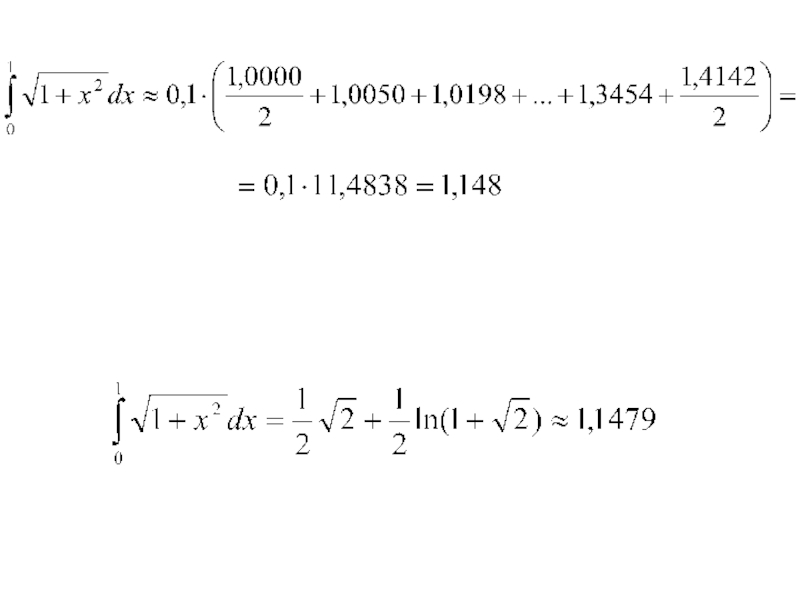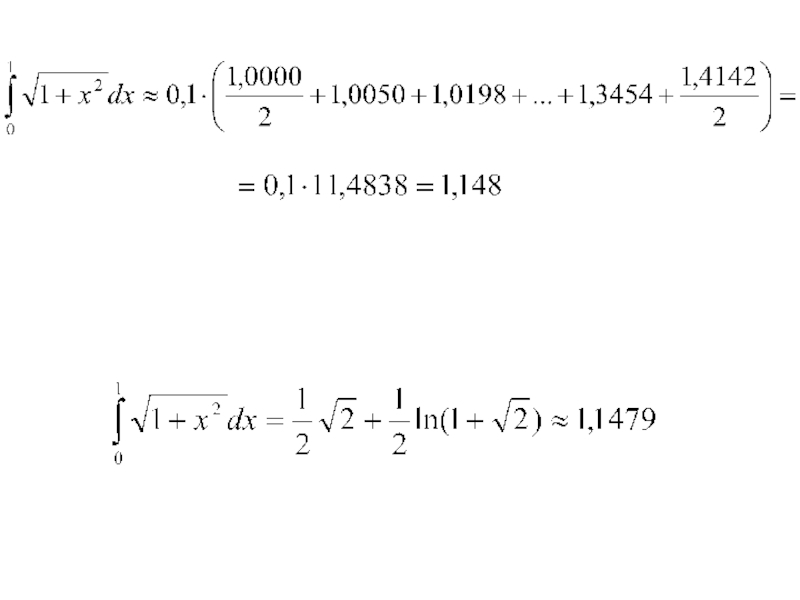Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение определенного интеграла Геометрическое приложение. Механическое приложение.
Содержание
- 1. Применение определенного интеграла Геометрическое приложение. Механическое приложение.
- 2. ? 1.1. Площадь плоской фигуры
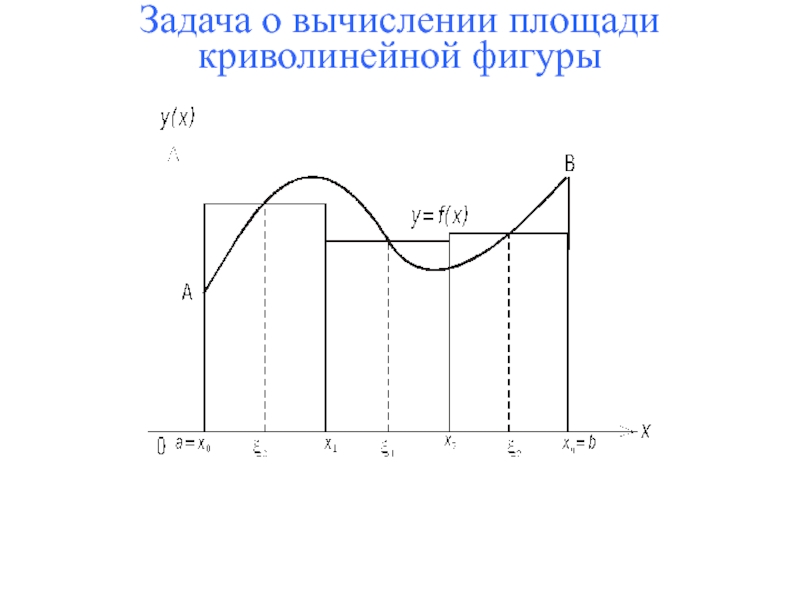
- 3. Задача о вычислении площади криволинейной фигуры
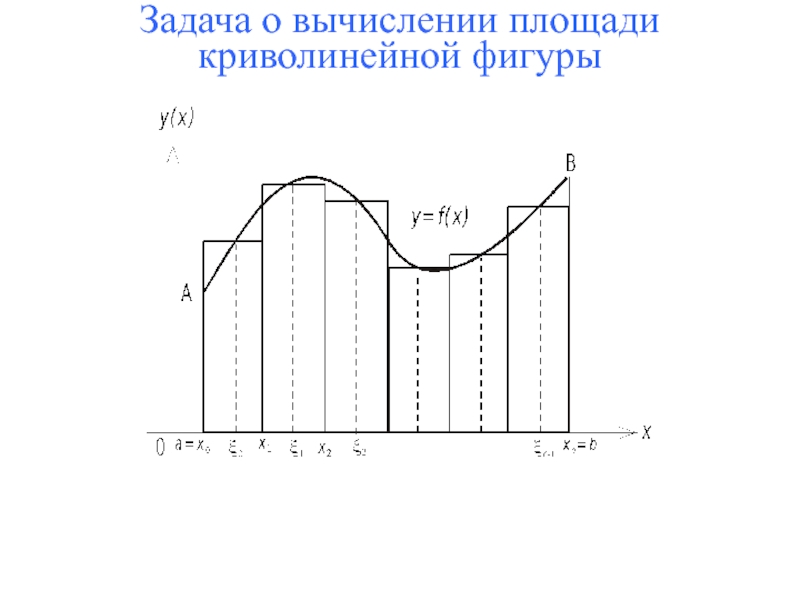
- 4. Задача о вычислении площади криволинейной фигуры
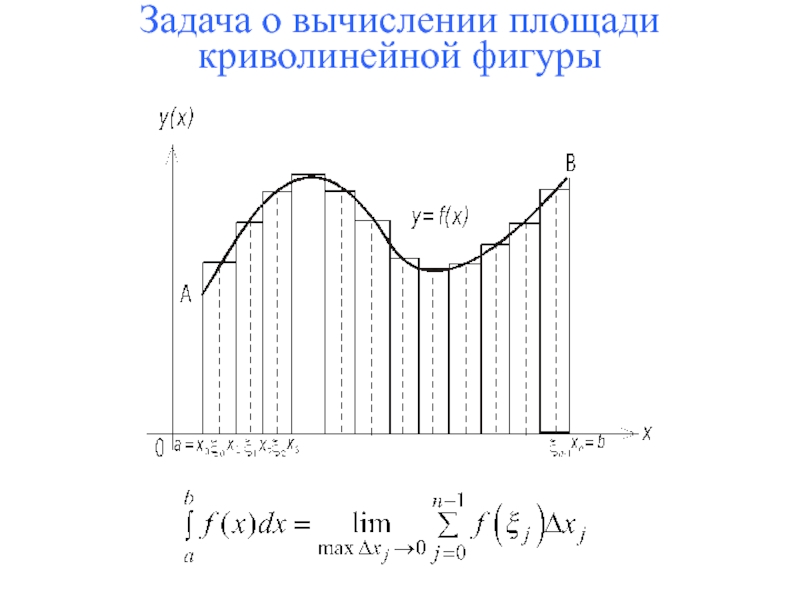
- 5. Задача о вычислении площади криволинейной фигуры
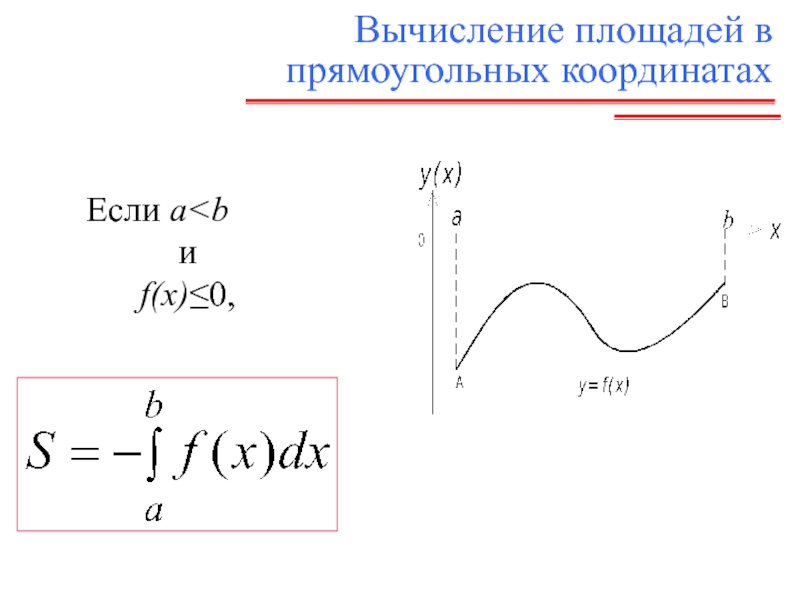
- 6. Вычисление площадей в прямоугольных координатах Если a
- 7. Вычисление площадей в прямоугольных координатах Если a
- 8. Пример: Найти площадь фигуры, заключенной между осью Ох и кривой –. .
- 9. Пример: Найти площадь фигуры,
- 10. Пример: Вычислить площадь, ограниченную синусоидой y = sin x и осью Ox, при 0 ≤х ≤2π –. .
- 11. Пример: Вычислить площадь, ограниченную синусоидой
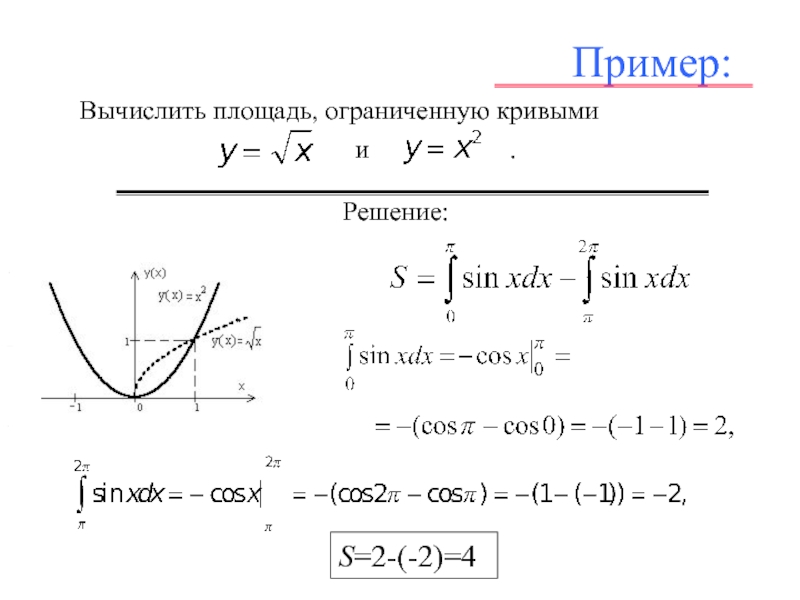
- 12. Вычислить площадь, ограниченную кривыми
- 13. Пример: Вычислить площадь, ограниченную кривыми
- 14. Вычисление площадей кривых, заданных параметрически Если кривая
- 15. Замечание Формулаприменима также для вычисления площади фигуры,
- 16. Пример: –. . Найти площадь петли кривой
- 17. Пример: Найти площадь петли
- 18. Пример: Найти площадь петли
- 19. Вычисление площадей в полярных координатахПлощадь криволинейного
- 20. Пример: Вычислить площадь лунки, ограниченной дугами окружностей . , , .
- 21. Пример: Вычислить площадь лунки, ограниченной
- 22. ? 1.2. Длина дуги кривой
- 23. В декартовых координатах:Если гладкая кривая задана
- 24. Пример: Найти длину полукубической параболы
- 25. Пример: Найти длину полукубической параболы
- 26. Кривая задана параметрически :x = x(t), y = y(t), (t1 ≤ t ≤ t2):
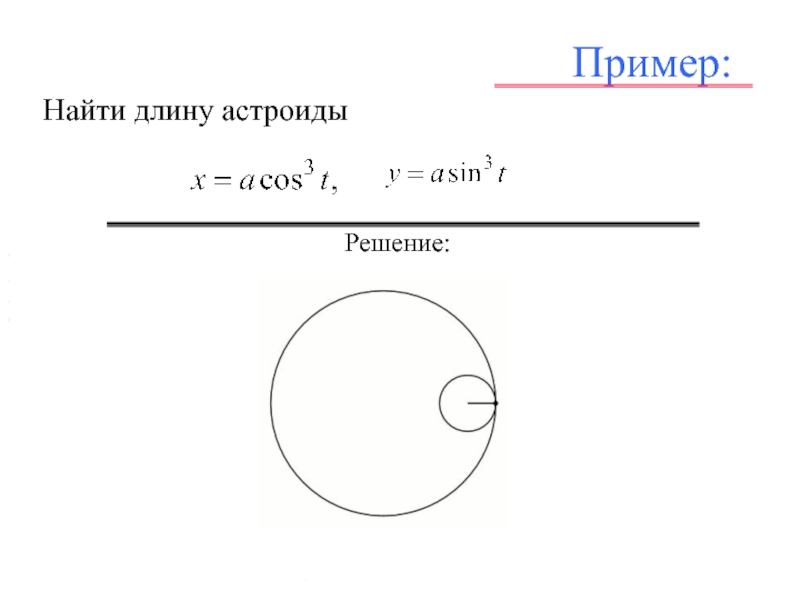
- 27. Пример: Найти длину астроиды . , , . Решение: , ,,
- 28. Пример: Найти длину астроиды . , , . Решение: , ,, , ,
- 29. Кривая задана параметрически :x = x(t), y = y(t), z = z(t), (t1 ≤ t ≤ t2):
- 30. В полярных координатахЕсли задано полярное уравнение гладкой кривой ρ = ρ (ϕ) и двумя лучами α ≤ ϕ ≤ β:
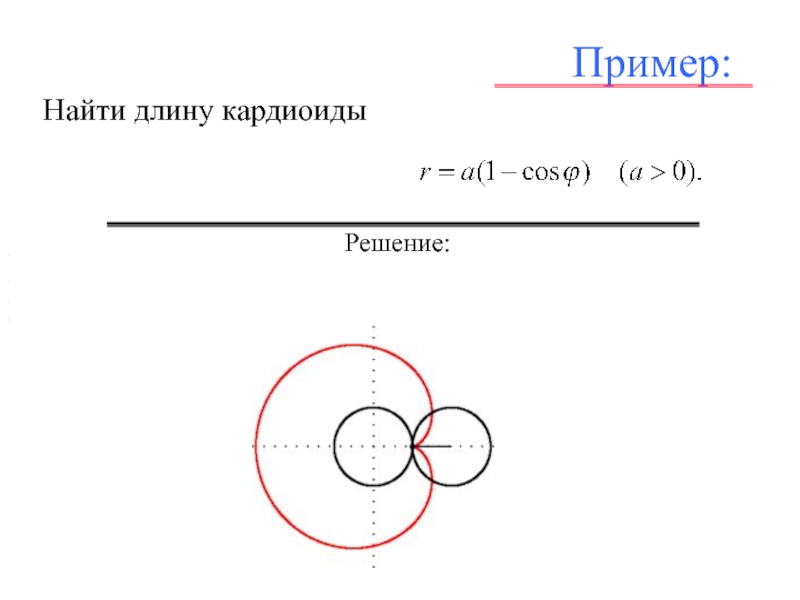
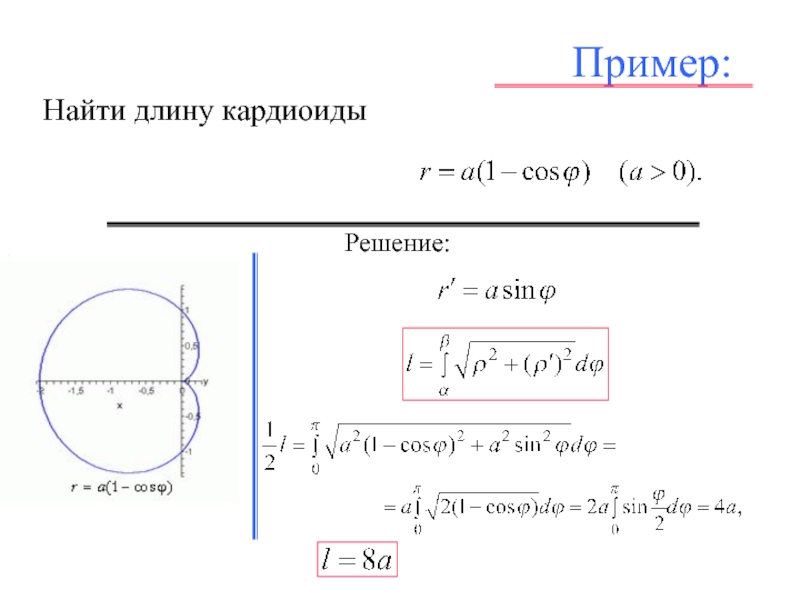
- 31. Пример: Найти длину кардиоиды . , , . Решение: , ,,
- 32. Пример: Найти длину кардиоиды . , , . Решение: , ,,
- 33. ? 1.3 Объем тела
- 34. Объем тела по площадям его параллельных
- 35. Пример: Найти объем тела,
- 36. Объем тела вращения Если криволинейная трапеция
- 37. Объем тела вращения
- 38. Пример: Найти объем тела,
- 39. Объем тела вращения Если криволинейный сектор,
- 40. Пример: , , . Решение: ,, ,
- 41. Площадь поверхности вращения Если криволинейная трапеция
- 42. Площадь поверхности вращения Если кривая задана
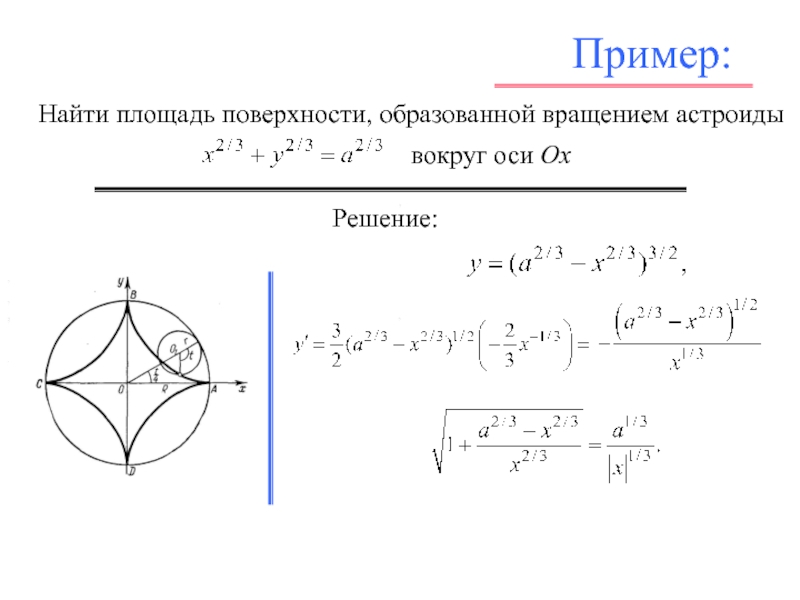
- 43. Пример: , , . Решение: ,, ,
- 44. Пример: , , . ,, ,
- 45. ? 2 Механическое приложение
- 46. Пройденный путь Путь, пройденный точкой за промежуток
- 47. Работа Работа, произведенная силой F при перемещении
- 48. Масса стержня переменной плотности Будем считать, что
- 49. ? 3 Приближенное вычисление
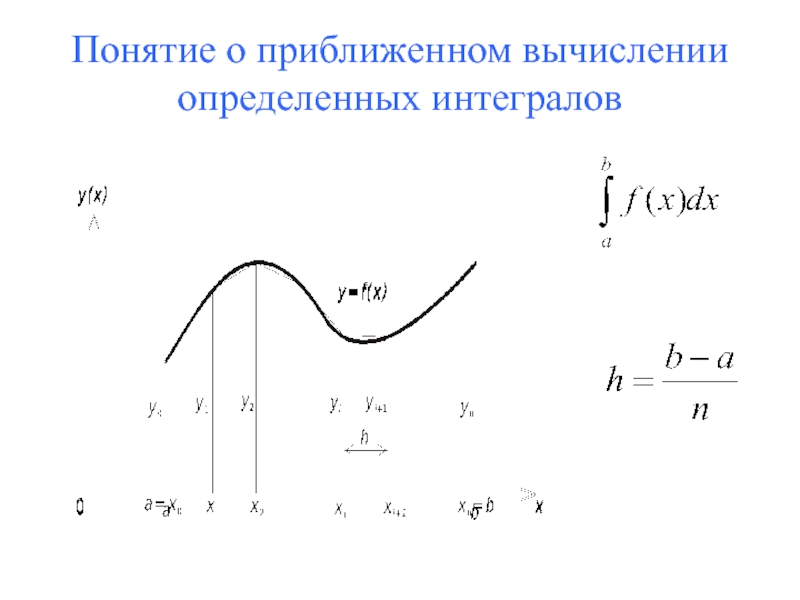
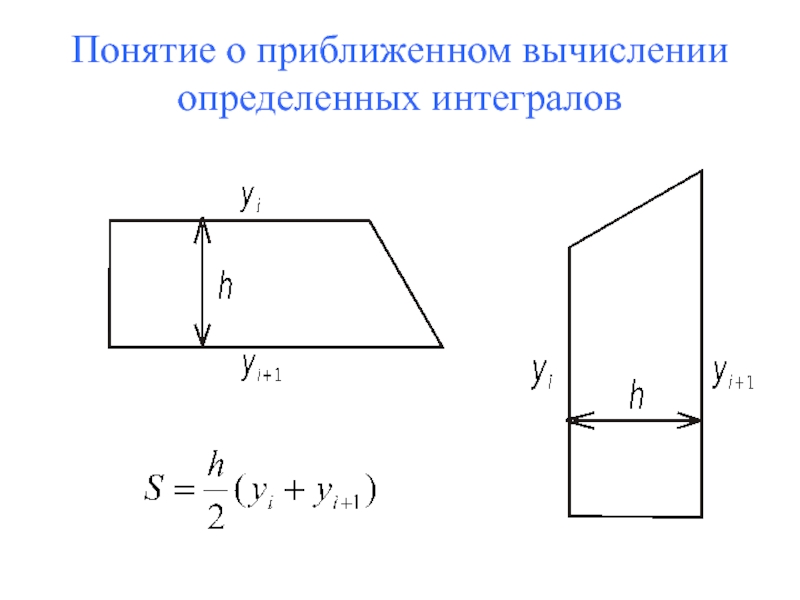
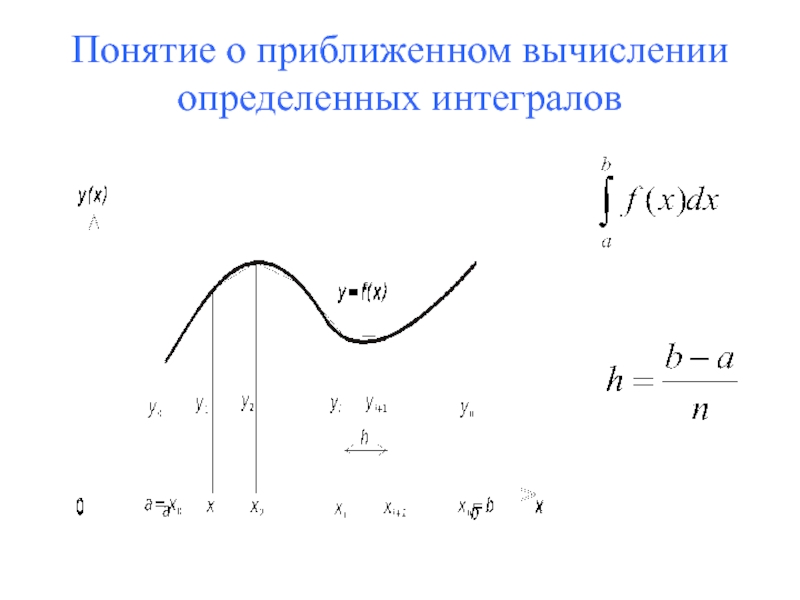
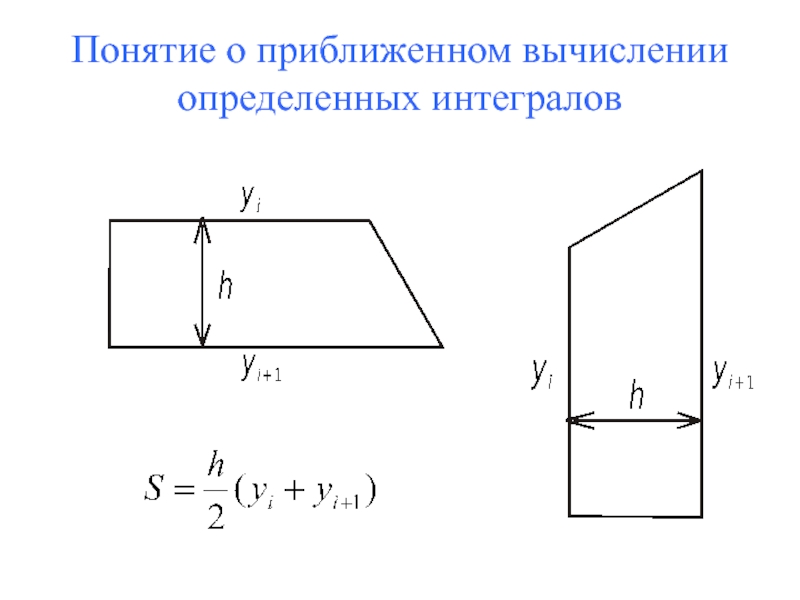
- 50. Понятие о приближенном вычислении определенных интегралов
- 51. Понятие о приближенном вычислении определенных интегралов
- 52. Слайд 52
- 53. h=0,1
- 54. Слайд 54
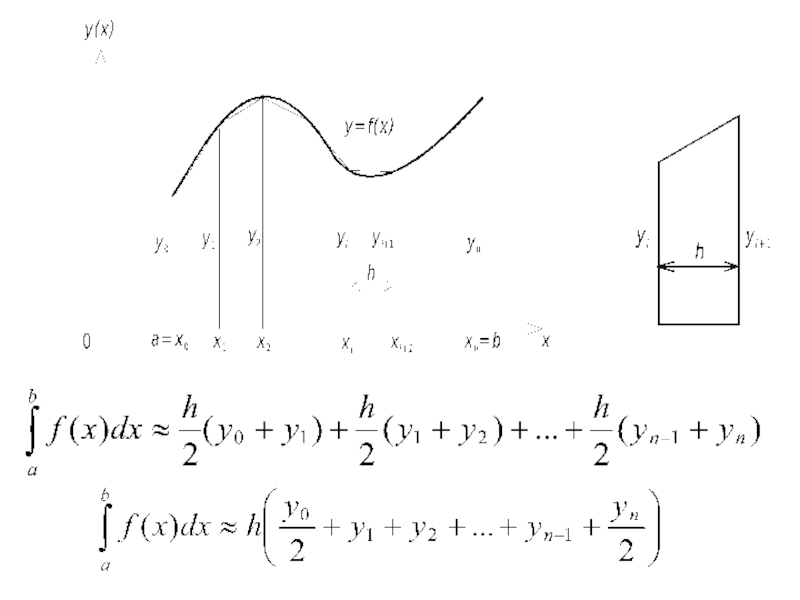
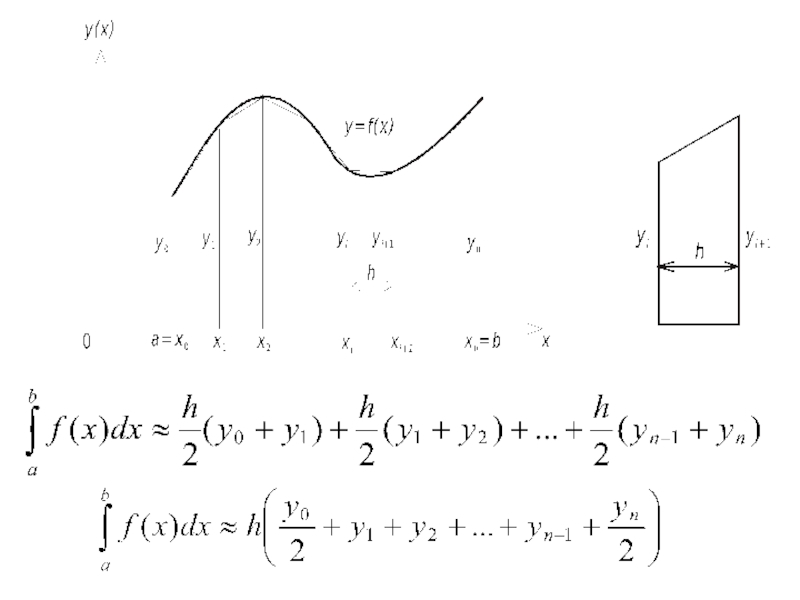
- 55. Понятие о приближенном вычислении определенных интегралов
- 56. Понятие о приближенном вычислении определенных интегралов
- 57. Слайд 57
- 58. h=0,1
- 59. Слайд 59
- 60. Спасибо за внимание!
- 61. Спасибо за внимание!
- 62. Скачать презентанцию
Слайды и текст этой презентации
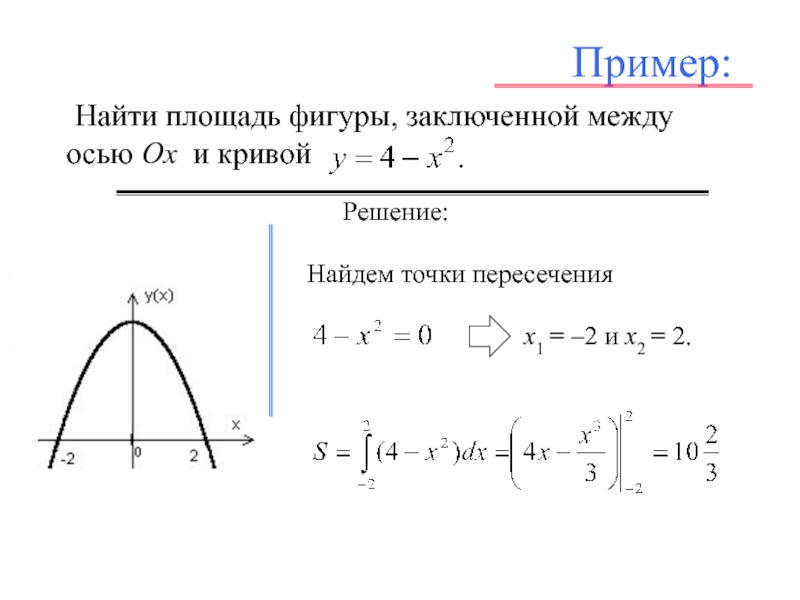
Слайд 9Пример:
Найти площадь фигуры, заключенной между осью Ох
и кривой
–
.
Решение:
.
Найдем точки пересечения
х1 = –2
и х2 = 2. Слайд 11Пример:
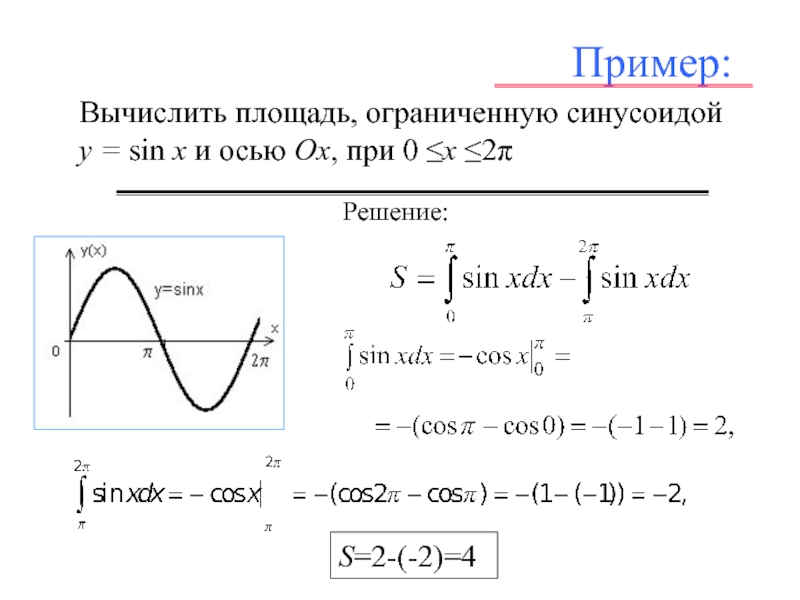
Вычислить площадь, ограниченную синусоидой y = sin x и осью Ox,
при 0 ≤х ≤2π
–
.
Решение:
.
S=2-(-2)=4
Слайд 14
Вычисление площадей кривых, заданных параметрически
Если кривая задана параметрическими уравнениями
х = x(t), y = y(t), то площадь криволинейной трапеции, ограниченной этой кривой, прямыми
x = a, x = b и отрезком [a, b] оси Ox:где t1 и t2 определяются из уравнений a = x(t1), b = x(t2) (y(t) ≥ 0 при t1 ≤ t ≤ t2)
Слайд 15
Замечание
Формула
применима также для вычисления площади фигуры, ограниченной замкнутой кривой
(изменение параметра t от t1 до t2 должно соответствовать обходу
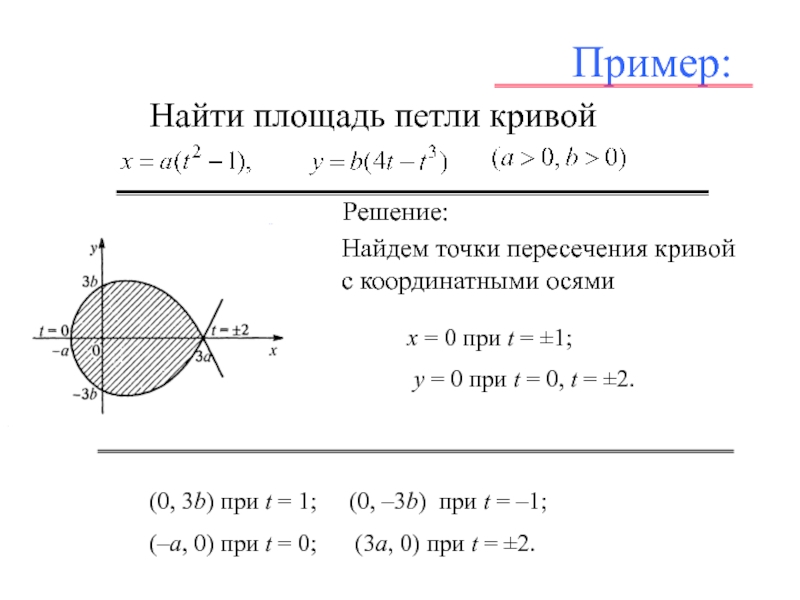
контура по часовой стрелке).Слайд 17Пример:
Найти площадь петли кривой
–
.
Решение:
.
Найдем
точки пересечения кривой
с координатными осями
х = 0 при t = ±1;
y = 0
при t = 0, t = ±2.(0, 3b) при t = 1; (0, –3b) при t = –1;
(–a, 0) при t = 0; (3a, 0) при t = ±2.
Слайд 18Пример:
Найти площадь петли кривой
.
Решение:
(0, 3b)
при t = 1; (0, –3b) при t = –1;
(–a, 0) при t = 0; (3a, 0) при
t = ±2.
Слайд 19
Вычисление площадей
в полярных координатах
Площадь криволинейного сектора,
ограниченного кривой, заданной
в полярных координатах уравнением ρ = ρ (ϕ) и двумя лучами ϕ = α, ϕ = β (α
Слайд 21Пример:
Вычислить площадь лунки, ограниченной дугами окружностей
.
Решение:
,
,
.
Окружности пресекаются при
.
Слайд 23
В декартовых координатах:
Если гладкая кривая задана уравнением y = f(x),
то длина
l ее дуги:
где a и b – абсциссы концов дуги.
Слайд 25Пример:
Найти длину полукубической параболы
от
начала координат до точки (4, 8).
.
,
,
.
Решение:
,
,
Слайд 30
В полярных координатах
Если задано полярное уравнение гладкой кривой ρ = ρ (ϕ) и
двумя лучами α ≤ ϕ ≤ β:
Слайд 34
Объем тела по площадям его параллельных сечений
Если площадь S(x)
сечения тела плоскостью, перпендикулярной оси Ох, является непрерывной функцией на
отрезке [a, b], то объем тела:где а, b – левая и правая границы тела.
Слайд 35Пример:
Найти объем тела, основание которого – круг радиуса
а, а сечение плоскостью, перпендикулярной фиксированному диаметру круга, есть равнобедренный
треугольник высоты h..
,
,
.
Решение:
,
,
,
,
Слайд 36
Объем тела вращения
Если криволинейная трапеция ограничена графиком непрерывной функции
и
прямыми то объем тела, образованного вращением этой трапеции вокруг оси Ох, равен
Слайд 38Пример:
Найти объем тела, образованного вращением вокруг оси
Оу фигуры, ограниченной линиями
.
,
,
.
Решение:
,
,
,
,
Слайд 39
Объем тела вращения
Если криволинейный сектор, ограниченный кривой
и
лучами
вращается вокруг полярной оси,
то объем тела вращения равен
Слайд 40Пример:
,
,
.
Решение:
,
,
,
Кардиоида
вращается вокруг полярной
оси.
Найти объем тела вращения
Слайд 41
Площадь поверхности вращения
Если криволинейная трапеция ограничена графиком непрерывной функции
и
прямыми то площадь поверхности вращения, образованного вращением этой трапеции вокруг оси Ох, равна

































![Применение определенного интеграла Геометрическое приложение. Механическое приложение. Пройденный путь Путь, пройденный точкой за промежуток времени [t0, T], равен соответствующему Пройденный путь Путь, пройденный точкой за промежуток времени [t0, T], равен соответствующему определенному интегралу от скорости движения точкиЗамечание:Результат](/img/thumbs/948fdf9ebdaf4297ea8f45717a21ce93-800x.jpg)

![Применение определенного интеграла Геометрическое приложение. Механическое приложение. Масса стержня переменной плотности Будем считать, что отрезок [a ,b] оси х Масса стержня переменной плотности Будем считать, что отрезок [a ,b] оси х имеет массу с переменной линейной плотностью](/img/thumbs/11cfb09568d478942d1a7cc2733301e4-800x.jpg)