Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение производной функции для отыскания точек экстремума
Содержание
- 1. Применение производной функции для отыскания точек экстремума
- 2. Слайд 2
- 3. Слайд 3
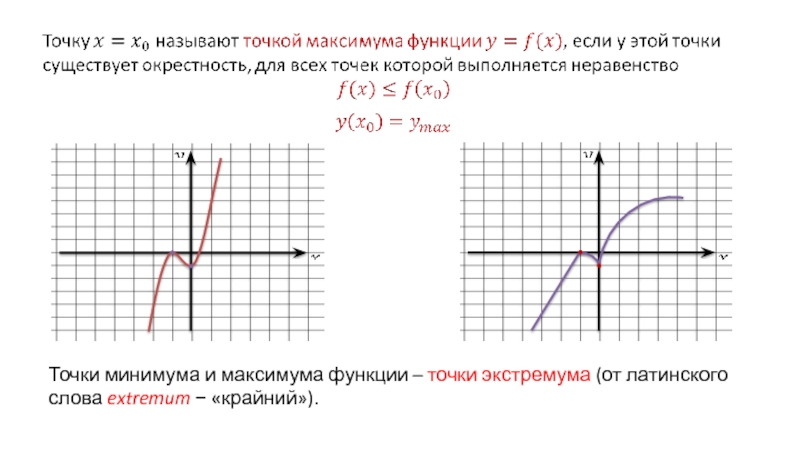
- 4. Точки минимума и максимума функции – точки экстремума (от латинского слова extremum − «крайний»).
- 5. Пьер Ферма (1601 – 1665 гг.)Леонард Эйлер (1707 – 1783 гг.)Колин Маклорен (1698 – 1746 гг.)
- 6. Внутренние точки области определения, в которых производная
- 7. Слайд 7
- 8. Слайд 8
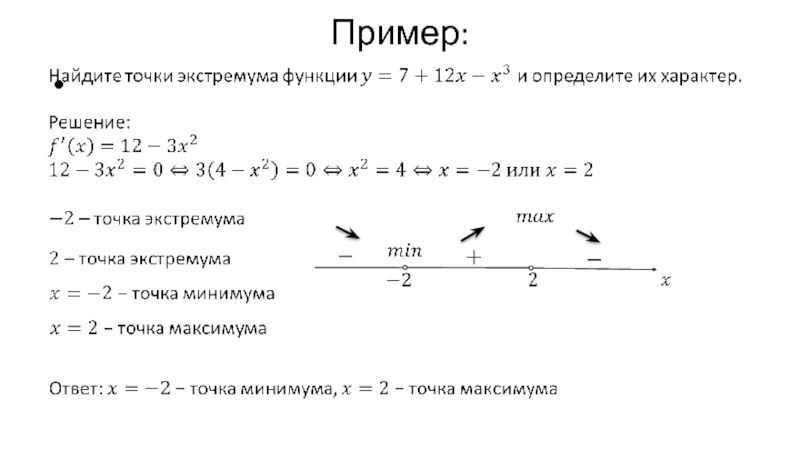
- 9. Пример:
- 10. Слайд 10
- 11. Пример:
- 12. Пример:
- 13. Скачать презентанцию
Точки минимума и максимума функции – точки экстремума (от латинского слова extremum − «крайний»).
Слайды и текст этой презентации
Слайд 4Точки минимума и максимума функции – точки экстремума (от латинского
слова extremum − «крайний»).
Слайд 6Внутренние точки области определения, в которых производная функции равна нулю,
называют стационарными, а внутренние точки области определения, в которых производная
функции непрерывна, но производная не существует, называют критическими.
