Слайд 1Лекция 6
Продукционная модель
Слайд 2Продукционная модель
Продукционная модель в силу своей простоты получила наиболее широкое
распространение. В этой модели знания представляются в виде совокупности правил
типа «ЕСЛИ - ТО».
Впервые идея появилась в работе Эмиля Поста (Emil Leon Post), 1943.
Продукционная система эквивалентна машине Тьюринга.
Любое продукционное правило, содержащееся в БЗ, состоит из двух частей: антецедента и консеквента.
Слайд 3Продукционная модель
Антецедент представляет собой посылку правила (условную часть) и состоит
из элементарных предложений, соединенных логическими связками И, ИЛИ.
Консеквент (заключение)
включает одно или несколько предложений, которые выражают либо некоторый факт, либо указание на определенное действие, подлежащее исполнению.
АНТЕЦЕДЕНТ → КОНСЕКВЕНТ
Слайд 4Продукционная модель
Примеры Продукционных правил:
ЕСЛИ «двигатель не заводится» И «стартер двигателя
не работает», ТО «неполадки в системе электропитания стартера»;
ЕСЛИ «животное имеет
перья», ТО «животное - птица».
Антецеденты и консеквенты правил формируются из атрибутов и значений, например:
Атрибут Значение
Двигатель Не заводится
Стартер двигателя Не работает
Животное Имеет перья
Животное Птица
Слайд 5Продукционная модель
Более широкие возможности имеет способ описания с помощью триплетов
объект—атрибут- значение. В этом случае отдельная сущность предметной области рассматривается
как объект, а данные, хранящиеся в рабочей памяти, показывают значения, которые принимают атрибуты этого объекта.
Примеры триплетов:
собака — кличка — Граф;
собака — порода - ризеншнауцер;
собака - окрас — черный.
Слайд 6Продукционная модель
Одним из преимуществ такого представления знаний является уточнение контекста,
в котором применяются правила. Например, правило, относящееся к объекту «собака»,
должно быть применимо для собак с любыми кличками, всех пород и окрасок. С введением триплетов правила из базы правил могут срабатывать более одного раза в процессе одного логического вывода, поскольку одно правило может применяться к различным экземплярам объекта (но не более одного раза к каждому экземпляру).
Слайд 7Продукционная модель
В рабочей памяти продукционной системы хранятся пары атрибут -
значение, истинность которых установлена в процессе решения конкретной задачи к
некоторому текущему моменту времени. Содержимое рабочей памяти изменяется в процессе решения задачи. Это происходит по мере срабатывания правил.
Слайд 8Продукционная модель
Правило срабатывает, если при сопоставлении фактов, содержащихся в рабочей
памяти, с антецедентом анализируемого правила имеет место совпадение, при этом
заключение сработавшего правила заносится в рабочую память. Поэтому в процессе логического вывода объем фактов в рабочей памяти, как правило, увеличивается (уменьшаться он может в том случае, если действие какого-нибудь правила состоит в удалении фактов из рабочей памяти). В процессе логического вывода каждое правило из базы правил может сработать только один раз.
Слайд 9Продукционная модель
Прямой порядок — от фактов к заключениям. В экспертных
системах с прямыми выводами по известным фактам отыскивается заключение, которое
из этих фактов следует. Если такое заключение удается найти, оно заносится в рабочую память.
Прямой порядок применяется в задачах, где на основании имеющихся фактов необходимо определить тип (класс) объекта или явления, выдать рекомендацию, определить диагноз и т.п.
Все или большинство данных заданы в пространстве задачи.
Слайд 10Продукционная модель
Существует большое количество потенциальных целей, но всего лишь несколько
способов представления и применения исходных фактов.
Сформировать цель или гипотезы
очень трудно в силу избыточности исходных данных или большого числа конкурирующих гипотез.
Слайд 11Продукционная модель
Обратный порядок вывода — от заключений к фактам. В
системах с обратным выводом вначале выдвигается некоторая гипотеза о конечном
суждении, а затем механизм вывода пытается найти в рабочей памяти факты, которые могли бы подтвердить или опровергнуть выдвинутую гипотезу. Процесс отыскания необходимых фактов может включать достаточно большое число шагов, при этом возможно выдвижение новых гипотез (целей).
Слайд 12Продукционная модель
Механизм вывода включает компоненту вывода и управляющую компоненту.
Компонента вывода.
Ее действие основано на применении правила логического вывода. Суть состоит
в следующем. Если в РП присутствует истинный факт А и в БП существует правило вида «ЕСЛИ А, ТО В», то факт В признается истинным и заносится в РП. Такой вывод легко реализуется на ЭВМ, однако при этом часто возникают проблемы, связанные с распознаванием значений слов, а также с тем, что факты могут иметь внутреннюю структуру и между элементами этой структуры возможны различного рода связи.
Слайд 13Продукционная модель
Например, пусть имеется факт
А — «Автомобиль Иванова —
белый»
и правило «ЕСЛИ Автомобиль — белый, ТО Автомобиль легко
заметить ночью».
Человек легко выведет заключение «Автомобиль Иванова легко заметить ночью», но это не под силу ЭС чисто продукционного типа. Она не сможет сформировать такое заключение, потому что А не совпадает точно с антецедентом правила.
Слайд 14Продукционная модель
Управляющая компонента.
Она определяет порядок применения правил, а
также устанавливает, имеются ли еще факты, которые могут быть изменены
в случае продолжения работы. Механизм вывода работает циклически, при этом в одном цикле может сработать только одно правило.
Слайд 15Продукционная модель
В цикле выполняются следующие основные операции:
сопоставление — образец (антецедент)
правила сравнивается с имеющимися в РП фактами;
разрешение конфликтного набора —
выбор одного из нескольких правил в том случае, если их можно применить одновременно;
Слайд 16Продукционная модель
срабатывание правила — в случае совпадения образца некоторого правила
из базы правил с фактами, имеющимися в рабочей памяти, происходит
срабатывание правила, при этом оно отмечается в БП;
действие — изменение содержимого РП путем добавления туда заключения сработавшего правила. Если в заключении содержится директива на выполнение некоторой процедуры, последняя выполняется.
Слайд 17Стратегии разрешения конфликтов
Стратегии разрешения конфликтов отличаются в различных реализациях продукционной
модели и могут быть достаточно простыми, например:
Рефракция (refraction) для
предотвращения зацикливания: после активизации правила оно не может быть использовано снова, пока не измениться содержимое рабочей памяти.
Слайд 18Стратегии разрешения конфликтов
Новизна (recency) позволяет сосредоточить поиск на одной линии
рассуждения: предпочтение отдается правилам, в условии которых встречаются факты, добавленные
в рабочую память последними.
Специфичность (specifity) отдает предпочтение более конкретным правилам перед более общими: одно правило более специфично (конкретно), чем другое, если оно содержит больше фактов в условной части.
Слайд 19Примеры продукций
ЕСЛИ клиент работает на одном месте более двух лет,
ТО клиент имеет постоянную работу.
ЕСЛИ клиент имеет постоянную работу И
клиенту более 18 лет И клиент НЕ имеет финансовых обязательств, ТО клиент может претендовать на получение кредита.
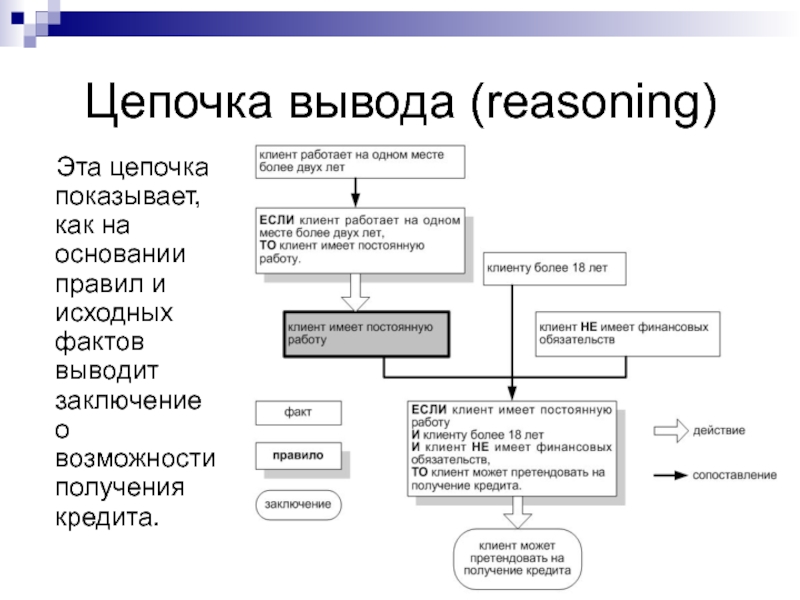
Слайд 20Цепочка вывода (reasoning)
Эта цепочка показывает, как на основании правил и
исходных фактов выводит заключение о возможности получения кредита.
Слайд 21Разновидности цепочек вывода
Монотонным выводом в продукционных системах называют вывод, при
котором факты не удаляются из рабочей памяти.
Немонотонный вывод допускает удаление
фактов из рабочей памяти. При немонотонном выводе существенную роль играет порядок применения продукционных правил.
Слайд 22Направления вывода
Вывод на основе данных (data–driven search), процесс решения задачи
начинается с исходных фактов. Затем применяя допустимые правила, осуществляется переход
к новым фактам. И так до тех пор, пока цель не будет достигнута. Это процесс также называют прямой цепочкой вывода (forward chaining).
Слайд 23Направления вывода
Вывод от цели (goal–directed strategy) начинается от одной из
допустимых целей, и рассматриваются пути, ведущие к достижению этой цели.
Таким образом, определяется последовательность правил, позволяющих найти решение. Процесс повторяется для всех заданных в задаче целей. Такой способ поиска называют также обратной цепочкой вывода (backward chaining).
Слайд 24Продукционная модель
Пример прямого вывода.
Пусть в БП имеются следующие правила:
Правило
1. «ЕСЛИ Двигатель не заводится И Фары не горят, ТО
Сел аккумулятор».
Правило 2. «ЕСЛИ Указатель бензина находится на нуле, ТО Двигатель не заводится».
Факты:
“Фары не горят и Указатель бензина находится на нуле”.
Слайд 25Продукционная модель
Основные шаги алгоритма прямого вывода:
1. Сопоставление фактов из РП
с образцами правил из БП. Правило 1 не может сработать,
а Правило 2 срабатывает, так как образец, совпадающий с его антецедентом, присутствует в РП.
2. Действие сработавшего Правила 2. В РП заносится заключение этого правила — образец “Двигатель не заводится”.
Слайд 26Продукционная модель
3. Второй цикл сопоставления фактов в РП с образцами
правил. Теперь срабатывает Правило 1, так как конъюнкция условий в
его антецеденте становится истинной.
4. Действие Правила 1, которое заключается в выдаче пользователю окончательного диагноза — Сел аккумулятор.
5. Конец работы (БП исчерпана).
Слайд 27Пример прямого вывода
(база знаний)
Пример миниатюрной экспертной системы для фондовой биржи.
БЗ включает, следующие продукционные правила:
ЕСЛИ Процентные ставки падают, ТО Уровень цен
на бирже растет.
ЕСЛИ Процентные ставки растут, ТО Уровень цен на бирже падает.
Слайд 28Пример прямого вывода
(база знаний)
ЕСЛИ Валютный курс доллара падает, ТО Процентные
ставки растут.
ЕСЛИ Валютный курс доллара растет, ТО Процентные ставки падают.
ЕСЛИ
Процентные ставки федерального резерва падают И Средства федерального резерва добавлены, ТО Процентные ставки падают.
Слайд 29Пример прямого вывода (начальное состояние)
На основании запроса пользователя инициализируется исходное
состояние рабочей памяти путем добавления в нее факта:
Валютный курс доллара
падает:
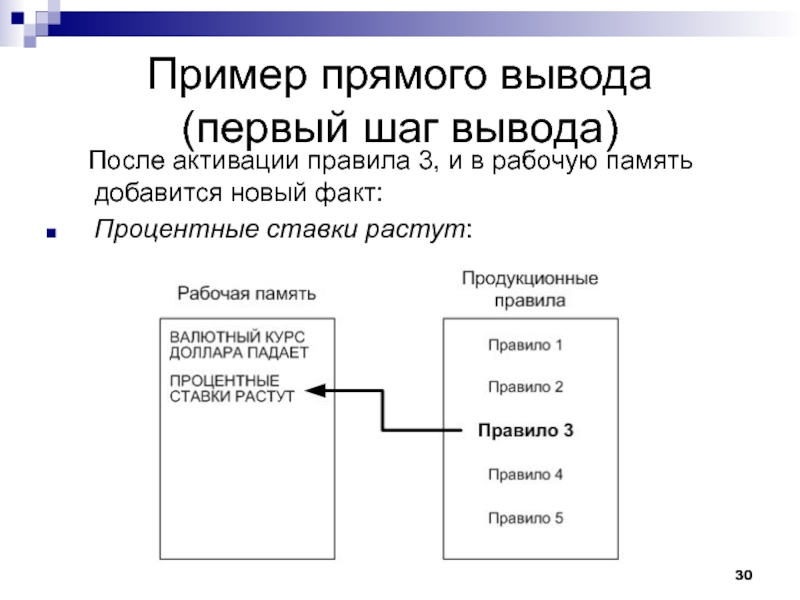
Слайд 30Пример прямого вывода
(первый шаг вывода)
После активации правила 3, и в
рабочую память добавится новый факт:
Процентные ставки растут:
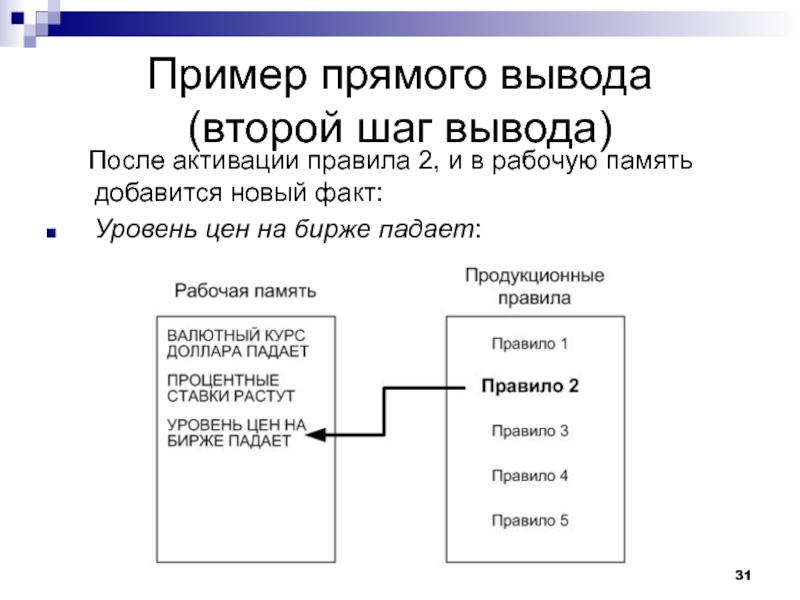
Слайд 31Пример прямого вывода
(второй шаг вывода)
После активации правила 2, и в
рабочую память добавится новый факт:
Уровень цен на бирже падает:
Слайд 32Продукционная модель
Пример прямого вывода с конфликтным набором.
Пусть в БП
имеются следующие правила:
Правило 1. «ЕСЛИ Двигатель не заводится И Фары
не горят, ТО Сел аккумулятор».
Правило 2. «ЕСЛИ Указатель бензина находится на нуле, ТО Двигатель не заводится».
Правило 3: «ЕСЛИ Указатель бензина находится на нуле, ТО Нет бензина.
Факты:
Фары не горят и Указатель бензина находится на нуле
Слайд 33Продукционная модель
Сопоставление фактов из РП с образцами правил из БП.
Возможно применение двух правил — Правила 2 и Правила 3,
т.е. возникает конфликтный набор и встает задача выбора: какое из этих правил применить первым.
Слайд 34Продукционная модель
2. Выбираем Правило 2, в РП добавится факт “Двигатель
не заводится” и на следующем шаге опять возникнет конфликтный набор,
так как можно будет применить Правило 1 и Правило 3.
3. Если будет выбрано Правило 1, то к заключению Сел аккумулятор придем за два шага. При любом другом выборе порядка применения правил к этому же заключению приходим за три шага
Слайд 35Обратная цепочка рассуждений
Обратная цепочка рассуждений применяется в задачах, соответствующих процессу
проверки гипотез при решении проблем человеком — для заданной ситуации
необходимо определить условия к ней приводящие.
Цель поиска явно присутствует в постановке задачи или может быть легко сформулирована.
Слайд 36Обратная цепочка рассуждений
Имеется слишком большое число правил, которые на основе
исходных фактов продуцируют возрастающее число заключений или целей. Своевременный отбор
целей позволяет отсеять множество тупиковых ветвей, что сокращает пространство поиска.
Исходные данные не приводятся в задаче, но подразумевается, что они должны быть известны или могут быть легко получены.
Слайд 37Продукционная модель
Пример обратного вывода.
Предположим, что в БП имеется два
правила (Правило 1 и Правило 2), а в РП —
те же факты, что в предыдущих примерах с прямым выводом.
Алгоритм обратного вывода содержит следующие шаги.
1. Выдвигается гипотеза окончательного диагноза — Сел аккумулятор.
2. Отыскивается правило, заключение которого соответствует выдвинутой гипотезе, в нашем примере — это Правило 1.
Слайд 38Продукционная модель
3. Исследуется возможность применения Правила 1, т.е. решается вопрос о
том, может ли оно сработать. Для этого в рабочей памяти
должны присутствовать факты, совпадающие с образцом этого правила. В рассматриваемом примере Правило 1 не может сработать из-за отсутствия в РП образца Двигатель не заводится. Этот факт становится новой целью на следующем шаге вывода.
4. Поиск правила, заключение которого соответствует новой цели. Такое правило есть - Правило 2.
5. Исследуется возможность применения Правила 2 (сопоставление). Оно срабатывает, так как в РП присутствует факт, совпадающий с его образцом.
Слайд 39Продукционная модель
6. Действие Правила 2, состоящее в занесении заключения Двигатель
не заводится в РП.
7. Условная часть Правила 1 теперь подтверждена
фактами, следовательно, оно срабатывает, и выдвинутая начальная гипотеза подтверждается.
8. Конец работы.
Слайд 40Продукционная модель
Пример обратного вывода с конфликтным набором. Предположим, что в
БП записаны Правило 1, Правило 2, Правило 3 и Правило
4:
«ЕСЛИ Засорился бензонасос, ТО Двигатель не заводится».
В РП присутствуют те же самые факты: Фары не горят и Указатель бензина находится на нуле.
Слайд 41Продукционная модель
Выдвигается гипотеза Сел аккумулятор.
Поиск правила, заключение которого совпадает с
поставленной целью. Это Правило 1.
Исследуется возможность применения Правила 1. Оно
не может сработать, выдвигается новая подцель “Двигатель не заводится”, соответствующая недостающему образцу.
Слайд 42Продукционная модель
Поиск правил, заключения которых совпадают с новой подцелью. Таких
правил два - Правило 2 и Правило 4. Если выберем
Правило 2, то дальнейшие шаги совпадают с примером без конфликтного набора. Если выберем Правило 4, то оно не сработает, так как в РП нет образца Засорился бензонасос. После этого будет применено Правило 2, что приведет к успеху, но путь окажется длиннее на один шаг.
Слайд 43Продукционная модель
Следует обратить внимание на то, что Правило 3, не
связанное с поставленной целью, вообще не затрагивалось в процессе вывода.
Этот факт свидетельствует о более высокой эффективности обратных выводов по сравнению с прямыми, так как при обратных выводах существует тенденция исключения из рассмотрения правил, не имеющих отношения к поставленной цели.
Слайд 44Продукционная модель
Продукционные модели часто используются при построении ЭС. Эта модель
удобна тем, что язык представления БД может выбираться произвольно в
зависимости от задачи (в предикатных языках БД представляется в виде набора предикатов).
Слайд 45Преимущества
продукционных моделей
Модульность
Модифицируемость
Доступность чтения
Способность к самообъяснению
Универсальность
Эффективность организации памяти
Слайд 46Удаление, изменение, добавление любой продукции может выполняться независимо от всех
остальных продукций (не приводит к изменениям в остальных продукциях). Знания
вводятся неупорядоченно как в словаре или энциклопедии. Практика показывает, что это естественный способ пополнения своих знаний для эксперта.
Модульность
Слайд 47Если добавляется или модифицируется какое-либо правило, то все, что было
сделано ранее, остается в силе и к новому правилу не
относится.
Каждое изменение обладает свойством аддитивности и локальности.
Модифицируемость
Слайд 48Подавляющая часть человеческих знаний может быть записана в виде продукций.
Человеческие знания являются модульными и поэтому продукционные системы более близки
для их представления и легки для чтения.
Доступность чтения
Слайд 49Системы продукций при необходимости могут реализовать любые алгоритмы и способны
отражать любое процедурное знание, доступное ЭВМ.
Универсальность
Слайд 50Это свойство связано и с правилами и с их структурами
внешнего управления. Система легко прослеживает цепочку правил, которую она использовала
для получения вывода.
Способность к самообъяснению
Слайд 511) Наличие в продукциях указателей на сферу применения продукции позволяет
эффективно организовать память, сократив время поиска в ней необходимой информации.
Классификация сфер может быть многоуровневой, что еще более повышает эффективность поиска знаний.
2) При объединении систем продукций и сетевых представлений получаются средства, обладающие большой вычислительной мощностью.
3) Параллелизм в системе продукций, асинхронность их реализации делают продукционные системы удобной моделью вычислений для ЭВМ новой архитектуры, в которой идея асинхронности и параллельности является центральной.
Эффективность
Слайд 52Недостатки продукционной системы:
При большом числе продукций становится сложной проверка
непротиворечивости системы продукций.
Из-за присущей системе недетерминированности (неоднозначного выбора выполняемой
продукции из фронта активизированных продукций) возникают принципиальные трудности при проверке корректности работы системы
Наблюдение из практики: если число продукций > 1000, то мало шансов, что система продукций во всех случаях будет правильно функционировать.
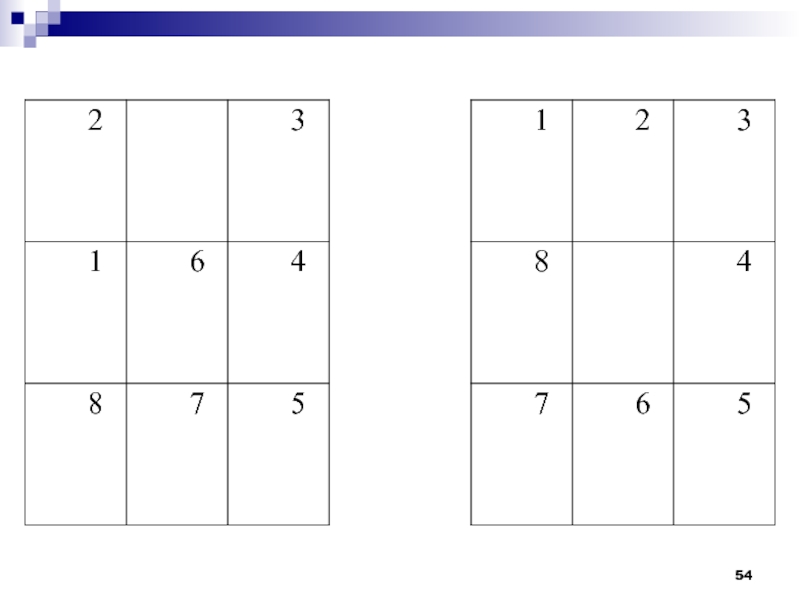
Слайд 53Пример. «Игра в восемь» (упрощенные пятнашки).
Задача. Дана доска, на которой
девять клеток, по которым перемещается восемь фишек. Их следует расположить
по порядку (см. рисунки 1 и 2).
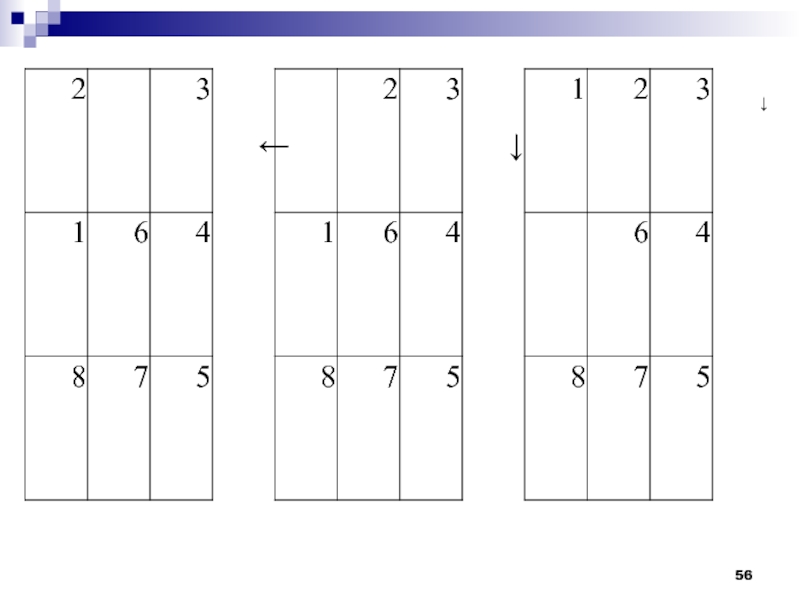
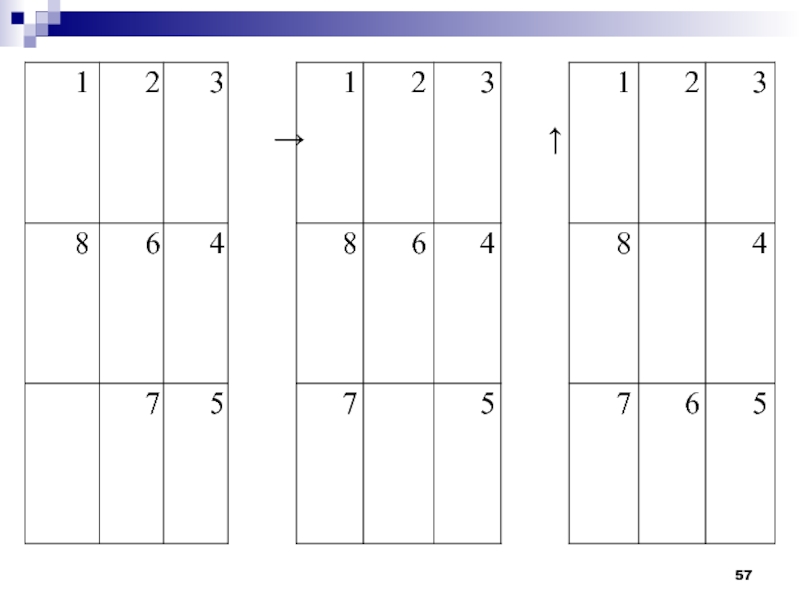
Слайд 55Сформулируем правила. Условно считаем, что мы как бы перемещаем не
фишки, а пустую клетку (дырку).
A) Если дырка не в верхнем
ряду, переместить ее вверх.
B) Если дырка не а правом столбце, переместить ее вправо.
С) Если дырка не в левом столбце, переместить ее влево.
D) Если дырка не в нижнем ряду, переместить ее вниз.
Слайд 58Продукционная модель
Экспертной системой (ЭС) называется система, которая позволяет пользователю описать
проблемную ситуацию и получить ее решение, сопровождаемое объяснениями, почему выбрано
именно это решение.
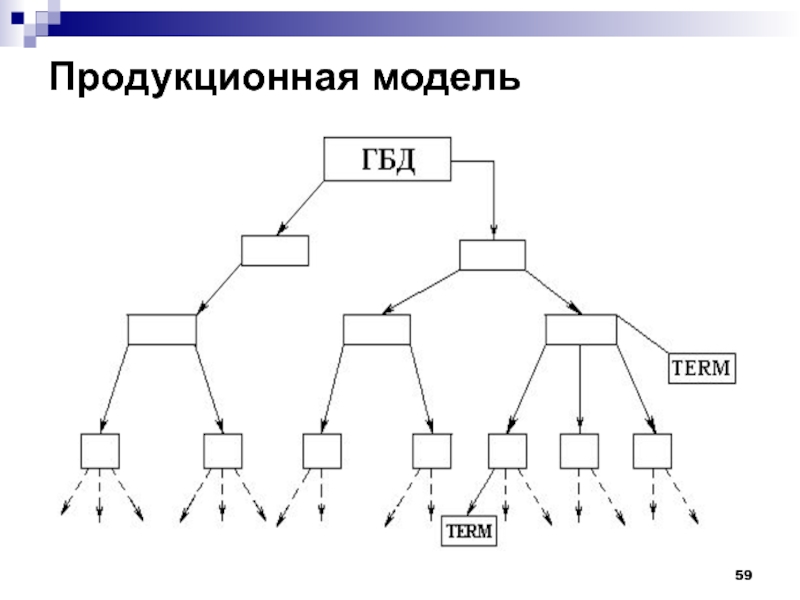
Основные компоненты ЭС.
ГБД – глобальная база данных (содержит исходную информацию, необходимую для решения проблемной ситуации).
БЗ – база знаний, суть набор операции преобразования ГБД (с помощью последовательности этих операций мы и получаем ответ, причем сама последовательность правил составляет определяет обоснование).
Стратегия выбора следующей операции.
Терминальное состояние ГБД (содержит ответ на вопрос).
Слайд 60Продукционная модель
Неотъемлемой частью ЭС, построенных на продукциях являются стратегии управления,
которые определяют порядок применения продукционных правил. Выделяют два класса стратегий.
A)
Безвозвратные стратегии. В этом случае существует критерий выбора очередного правила, после применения правила возврат к исходном состоянию (отмена применения правила) не производится никогда.
B) Пробные стратегии, которые, в свою очередь, делятся на два класса – поиск с возвратом (backtracking) и поиск в пространстве состояний (или поиск на графах).
Слайд 61Продукционная модель
Поиск с возвратом.
В начальный момент находимся в начальном состоянии
ГБД. Применяем какое-нибудь правило (выбираем его по определенному критерию). В
случае если приходим в тупик (не можем больше применить ни одно правило) возвращаемся на шаг назад. И так действуем до тех пор, пока не достигнем терминального состояния ГБД. В случае если произведен полный перебор вариантов, а терминальное состояние не достигнуто, значит задача неразрешима).
Слайд 62Продукционная модель
Классическим примером использования алгоритма поиска с возвратом является задача
о восьми ферзях. Её формулировка такова: «Расставить на стандартной 64-клеточной
шахматной доске 8 ферзей так, чтобы ни один из них не находился под боем другого». Сперва на доску ставят одного ферзя, а потом пытаются поставить каждого следующего ферзя так, чтобы его не били уже установленные ферзи. Если на очередном шаге такую установку сделать нельзя — возвращаются на шаг назад и пытаются поставить ранее установленного ферзя на другое место.
Слайд 63Продукционная модель
Общее число возможных расположений 8 ферзей на 64-клеточной доске
равно 4426165368. Общее число возможных расположений, удовлетворяющих условию задачи равно
92. В принципе, современные компьютеры уже позволяют произвести решение задачи (нахождение любого или всех решений) путём прямого перебора всех возможных вариантов расстановки, но обычно такое решение считается некорректным, и от решающего задачу требуется найти алгоритм, который позволял бы существенно сократить объём перебора.
Слайд 64Продукционная модель
Например, очевидно, что на одной горизонтали или вертикали доски
не может находиться больше одного ферзя, поэтому алгоритм решения изначально
не должен включать в перебор позиции, где два ферзя стоят на одной горизонтали или вертикали. Даже такое простое правило способно существенно уменьшить число возможных расположений: 16777216 (то есть 88) вместо 4426165368. Генерируя перестановки, которые являются решениями задачи о восьми ладьях и затем проверяя атаки по диагоналям, можно сократить число возможных расположений всего до 40320 (то есть 8!).
Слайд 65Продукционная модель
Один из типовых алгоритмов решения задачи — использование поиска с
возвратом: первый ферзь ставится на первую горизонталь, затем каждый следующий
пытаются поставить на следующую так, чтобы его не били ранее установленные ферзи. Если на очередном этапе постановки свободных полей не оказывается, происходит возврат на шаг назад — переставляется ранее установленный ферзь.
Слайд 66Продукционная модель
Но если решать более общую задачу об N ферзях,
то такой перебор вариантов даже с использованием описанных выше сокращений
будет весьма долго работать уже при N = 20, так как 20! = 2.433×1018. Поэтому представляет особенный интерес следующий эвристический алгоритм, решающий задачу об N ферзях на поле размером N x N. Он работает для всех N ≥ 4 или N = 1:
Слайд 67Продукционная модель
Разделить N на 12 и запомнить остаток (N будет
равно 8 для задачи о восьми ферзях).
Занести в список
все четные числа от 2 до N по порядку.
Если остаток равен 3 или 9, перенести 2 в конец списка.
Слайд 68Продукционная модель
Добавить в список все нечетные числа от 1 до
N по порядку, но, если остаток равен 8, перевернуть пары
соседних чисел (например: 3, 1, 7, 5, 11, 9, …).
Если остаток равен 2 и N ≥ 3, поменять местами 1 и 3, затем, если N ≥ 5, перенести 5 в конец списка.
Слайд 69Продукционная модель
Если остаток равен 3 или 9, переместить 1 и
3 (именно в этом порядке, а не в котором они
сейчас) в конец списка.
Разместить ферзя в первом стоблце и в строке с номером, равным первому элементу списка, затем поместить следующего ферзя во втором столбце и в строке с номером, равным второму элементу списка, и т.д.
Для N = 8 результат работы этого алгоритма показан на картинке.
Слайд 71Продукционная модель
Главный недостаток этого метода то, что возможно зацикливание. На
практике эта проблема решается путем введения ограничения на глубину поиска,
что, однако, в некоторых случаях может привести к ненахождению существующего решения.
Слайд 72Продукционная модель
Поиск в пространстве состояний (или поиск на графах).
Пусть дан
простой ориентированный граф G=(V,E), и пусть существует некоторая вершина S,
не имеющая предков (в эту вершину не входит ни одна дуга). Эта вершина называется начальным состоянием. Все остальные вершины имеют хотя бы одного предка. Также существует Term – подмножество терминальных вершин (состояний). Такой граф называется или пространством состояний или пространством решений, его вершины называются состояниями, а его дуги – правилами.
Слайд 73Поиск в пространстве состояний (или поиск на графах).
По существу, идея
очень проста. Множество проблем можно сформулировать в терминах трех важнейших
ингредиентов:
исходное состояние проблемы, например исходное состояние головоломки;
тест завершения — проверка, достигнуто ли требуемое конечное состояние или найдено решение проблемы (примером может послужить правило определения, собрана ли головоломка);
множество операций, которые можно использовать для изменения текущего состояния проблемы, например шаги или перемещения фигур при сборке головоломки.
Слайд 74Поиск в пространстве состояний (или поиск на графах).
Один из способов
представления такого концептуального пространства состояний — граф, в котором состояниям
соответствуют узлы, а операциям — дуги. Рассмотрим в качестве примера задачу построения слова из некоторого множества букв, как в игре Scrabble. Задавшись набором операций установки букв, можно сформировать пространство состояний.
Слайд 75Поиск в пространстве состояний (или поиск на графах).
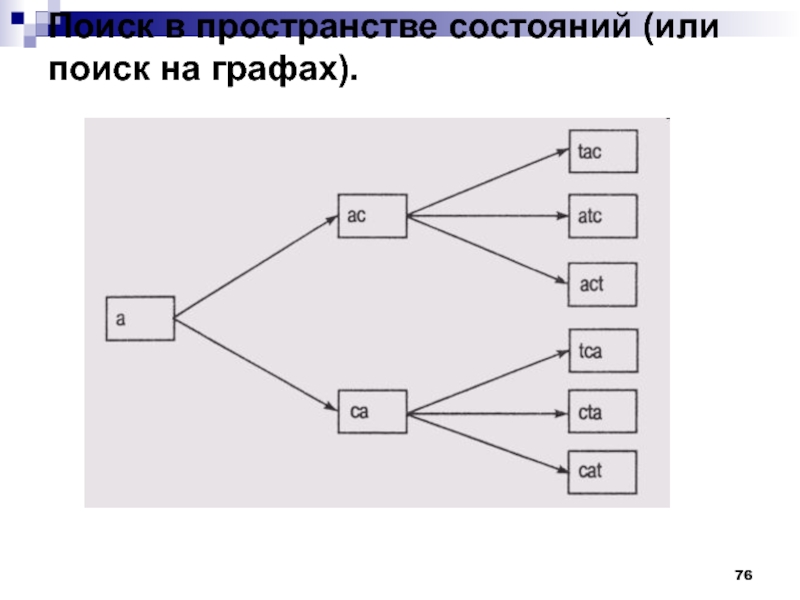
Предположим, что множество
доступных букв включает Т, С и А. На каждом уровне
графа мы будем добавлять по одной определенной букве. Каждая ветвь, исходящая из узла, соответствует установке буквы в определенную позицию в последовательности, а эта последовательность должна образовать осмысленное слово (рис. 2.1). Если это произошло, то головоломка считается собранной (например, если образовалась комбинация "act" или "cat").
Слайд 76Поиск в пространстве состояний (или поиск на графах).
Слайд 77Поиск в пространстве состояний (или поиск на графах).
Это пространство состояний
обладает двумя интересными свойствами, которые присущи далеко не всем пространствам
состояний:
оно конечно, поскольку существует только n! способов расставить n букв;
оно не содержит повторяющихся узлов, что может привести к образованию петель на графе.
Слайд 78Поиск в пространстве состояний (или поиск на графах).
Метод формирования анаграмм
последовательным перечислением является примером применения алгоритма, получившего наименование generate-and-test (порождение
и проверка).
(1) Генерировать новое состояние, модифицируя существующее; например, изменить последовательность букв, добавив новую в существующую последовательность.
(2) Проверить, не является ли образовавшееся состояние конечным (решением); например, проверить, не является ли образовавшаяся последовательность осмысленным словом. Если это так, то завершить, иначе перейти к шагу (1).
Слайд 79Поиск в пространстве состояний (или поиск на графах).
Множество решений, которые
удовлетворяют условию на шаге (2), иногда называют пространством решений. Алгоритм
имеет два основных варианта: поиск в глубину (depth-first search) и поиск в ширину (breadth-first search). Отличаются варианты порядком формирования состояний на шаге (1).
Слайд 80Поиск в пространстве состояний (или поиск на графах).
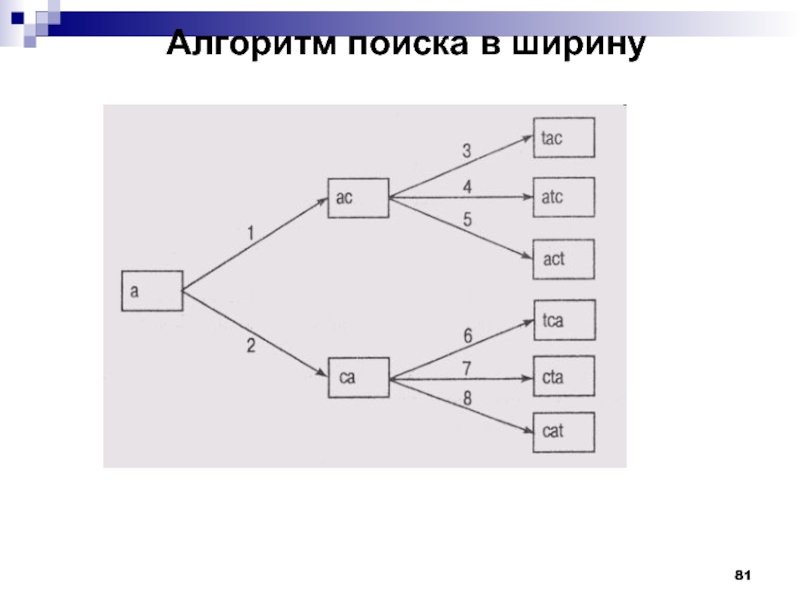
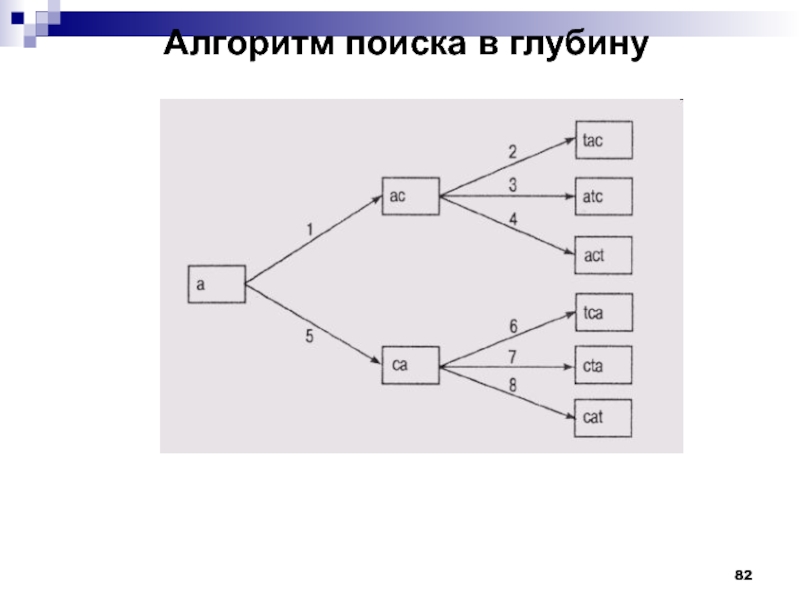
Для любого данного
узла N алгоритм поиска в глубину строит потомок этого узла,
т.е. формирует состояние, которое образуется в результате применения операторов к узлу N, а потом переходит к формированию узла, ближайшего к N, на том же уровне графа ("соседу" N), т.е. формирует состояние, которое образуется в результате применения оператора к узлу-родителю N. Алгоритм поиска в ширину действует наоборот — сначала формируются все "соседи" узла N, а потом уже строятся его потомки.
Слайд 83Поиск в пространстве состояний (или поиск на графах).
Оба алгоритма завершат
работу (найдут конечное состояние) после формирования узла "act", а не
"cat". Но алгоритму поиска в ширину придется для этого "посетить" пять узлов (сформировать и проанализировать пять состояний), а алгоритму поиска в глубину — четыре.
Отметим, что свойства этих алгоритмов существенно отличаются.
Слайд 84Поиск в пространстве состояний (или поиск на графах).
Алгоритм поиска в
ширину отыскивает решение, путь к которому на графе — кратчайший,
если таковое существует. Другими словами, он находит кратчайший путь между исходным состоянием и решением. Алгоритмы, обладающие таким свойством, называются разрешимыми (admissible).
Алгоритм поиска в глубину может быстрее найти решение, особенно, если при его выполнении используются эвристики для выбора очередной ветви. Но этот алгоритм может никогда не закончиться, если пространство состояний бесконечно.
Слайд 85Продукционная модель
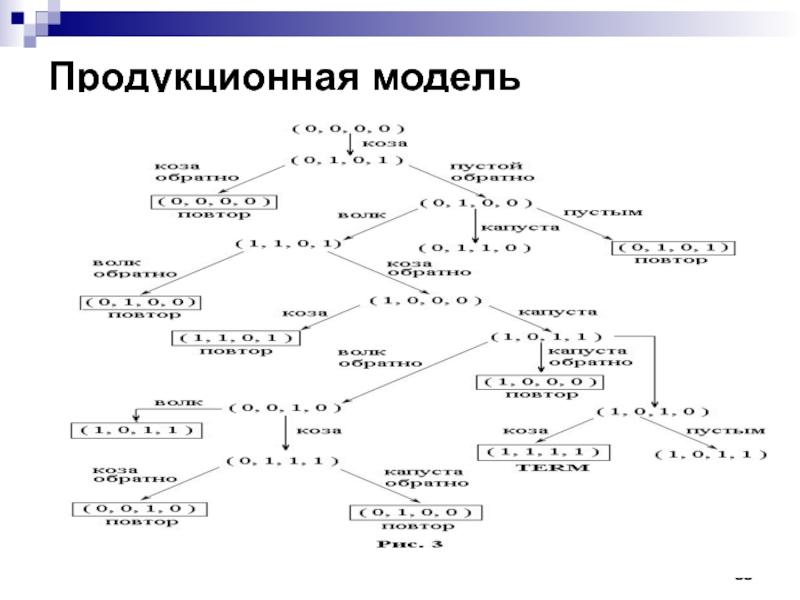
Пример. Формализация задачи о волке, козе и капусте. Есть
река и лодка, в которую входит лодочник и еще один
предмет. Козу и волка, а также козу и капусту нельзя оставлять вместе без присмотра. Задача – перевезти все с левого берега на правый.
Представление ГБД. (x-волк,y-коза,z-капуста,s-лодочник).
x,y,z,s = 0 - соответствующий предмет на левом берегу
x,y,z,s =1 – соответствующий предмет на правом берегу
Таким образом, (0,0,0,0) – исходное состояние, а (1,1,1,1) – терминальное состояние.
Слайд 86Продукционная модель
Прежде чем сформулировать правила, необходимо отсеять недопустимые состояния. Таковыми
являются состояния, предусматривающие одновременное нахождение волка и козы или козы
и капусты на берегу, противоположном от лодочника. Допустимые правила должны обеспечивать отсутствие возможности перехода в недопустимые состояния.