Слайд 1Теория вероятностей и математическая статистика
Проверка статистических гипотез
ЛЕКЦИЯ 14
Слайд 2Проверка статистических гипотез
Определение. Статистической гипотезой называется утверждение о виде распределения
генеральной совокупности.
Проверяемая гипотеза называется нулевой и обозначается H0.
Наряду с ней рассматривают альтернативную гипотезу H1.
Правило, согласно которому проверяют гипотезу H0 (принимают или отвергают), называется статистическим критерием.
Слайд 3Примеры гипотез
Гипотеза о виде распределения.
H0: F=F0, H1: F=F1.
(Или: H1:
F≠F0).
Гипотеза о параметре.
H0: θ= θ0, H1: θ = θ1.
(Или: H1: θ ≠ θ0).
Слайд 4Примеры гипотез
Гипотезы о параметре называются параметрическими гипотезами.
Например, H0:
θ= θ0, H1: θ = θ1 параметрические гипотезы.
Гипотеза называется
простой, если она
однозначно фиксирует распределение наблюдений. Иначе это сложная гипотеза.
H1: θ = θ1 – простая гипотеза, а
H1: θ ≠ θ0 – сложная.
Слайд 5Критерии согласия
Критериями согласия называют
критерии, предназначенные для проверки
простой гипотезы H0: F=F0,
при сложной
альтернативной H1: F≠F0.
Для проверки гипотезы возьмем статистику
T=T(X), характеризующую
отклонение
эмпирических данных от соответствующих
гипотезе теоретических значений.
(!) Должно быть известно (точно или
приближенно) распределение статистики T в
случае справедливости H0.
Слайд 6Проверка гипотезы
Определим для малого α >0 область V так, чтобы
вероятность осуществления события T(x)€ V в случае справедливости гипотезы H0
удовлетворяла бы условию P(T(x) € V ) = α.
По выборке вычислим значение статистики Т=tв
Если окажется, что tв € V, то в предположении справедливости гипотезы H0, произошло маловероятное событие и эта гипотеза должна быть отвергнута как противоречащая статистическим данным. В противном случае нет основания отказываться от рассматриваемой гипотезы и следует считать, что наблюдения не противоречат гипотезе (согласуются с ней).
Слайд 7
Статистика T(X), определенная выше,
называется статистикой критерия, V –
критической областью критерия,
α – уровнем
значимости критерия (вероятностью
ошибочного отвержения гипотезы H0,
когда она
верна).
В конкретных задачах величину α берут
равной 0,005; 0,01; 0,05; 0,1.
Обычно используют области вида V=(t*,+∞)
для неотрицательной статистики или
V=( – ∞ ,t1*) U(t2*, +∞), если статистика принимает
положительные и отрицательные значения.
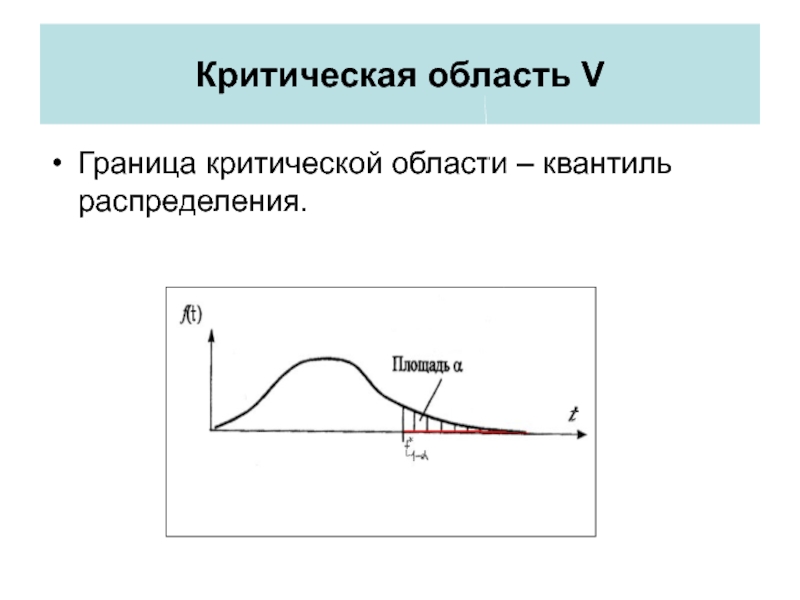
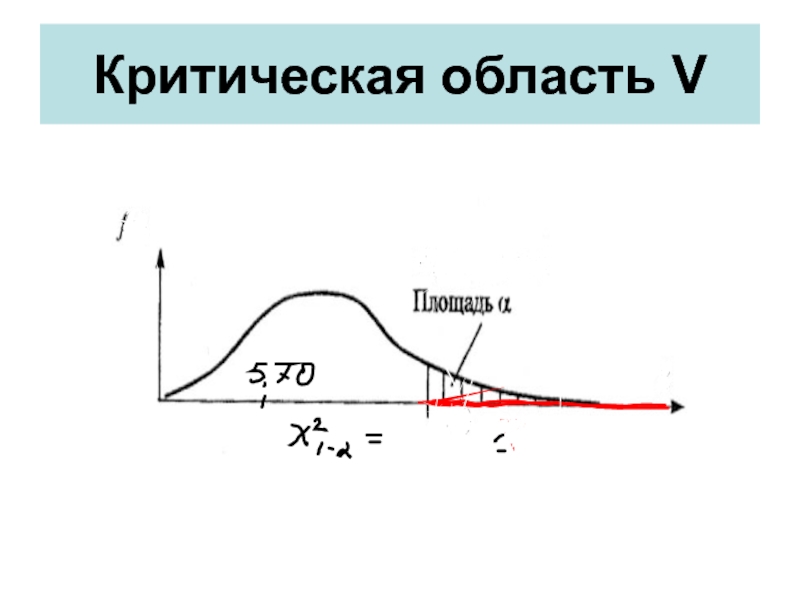
Слайд 8Критическая область V
Граница критической области – квантиль распределения.
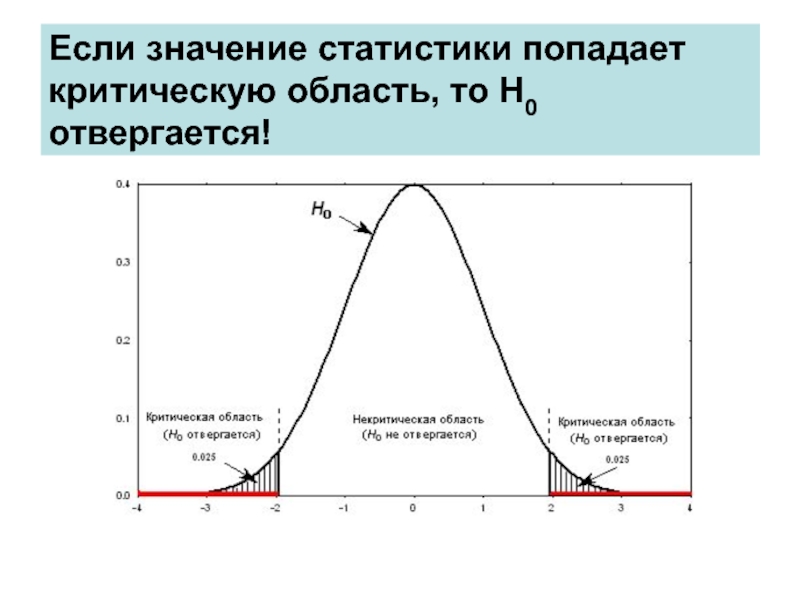
Слайд 9Если значение статистики попадает критическую область, то H0 отвергается!
Слайд 10H0: F=F0. Критерий согласия Колмогорова
Критерий применяется для непрерывных сл.в.
В качестве
статистики T выбирают величину
Dn=Dn(x)=max|Fn(x) –F0(x)|,
где Fn(x)– эмпирическая функция
распределения, а в качестве критической области – область вида V=(t*,+∞).
Слайд 11При n→∞, если H0 – верная гипотеза,
распределение статистики √n
Dn сходится к
функции Колмогорова К(t). Функция
Колмогорова задается таблично.
При
практических расчетах значения К(t) можно
применять уже при n>20.
t* находится из таблиц К(t) по заданному α.
Например, при α=0,05 находим, что t* = 1,358.
Слайд 12
Таким образом, при заданном уровне
значимости α правило проверки
гипотезы H0
при n>20 сводится к
следующему:
если значение статистики √n Dn ≥ t*,
то H0 отвергают, в противном случае
делают вывод , что статистические
данные не противоречат гипотезе.
Слайд 13H0: F=F0. Пример
Пусть α=0,05, а максимальное расхождение
между
F0 и эмпирической функцией
распределения Fn, построенной по выборке
объема
n=100, равно 0,094.
√100∙ 0,094= 0,94< t* = 1,358.
Следовательно, H0 не отвергается, т.е.
распределение F0 можно использовать для
моделирования генеральной совокупности.
Слайд 14
Критерий применяется к группированной выборке.
Пусть n – объем выборки
(n ≥50),
k – число интервалов группировки,
ni –
число значений, попавших в i –й интервал, i=1,…,k, (ni ≥5),
pi – теоретическая вероятность попадания одного элемента выборки в i –й интервал.
H0: F=F0. Критерий согласия Пирсона χ2
Слайд 15
Обозначим npi как niТ ( теоретические частоты)
Статистика критерия:
Слайд 16
Для нахождения теоретических вероятностей pi надо знать параметры. Если параметры
неизвестны (как обычно и бывает), то вместо них используются их
оценки.
Если используются оценки максимального правдоподобия, то :
Слайд 17
ν – параметр распределения χ2, называемый
числом степеней свободы.
ν =k
–r –1, где r – число параметров, оцененных
по выборке.
Критическая
область имеет вид (t*,+∞), где t*
– квантиль распределения χ2 порядка 1 –α.
Если значение статистики T ≥ t*, то H0
отвергают, в противном случае делают
вывод, что статистические данные не
противоречат гипотезе.
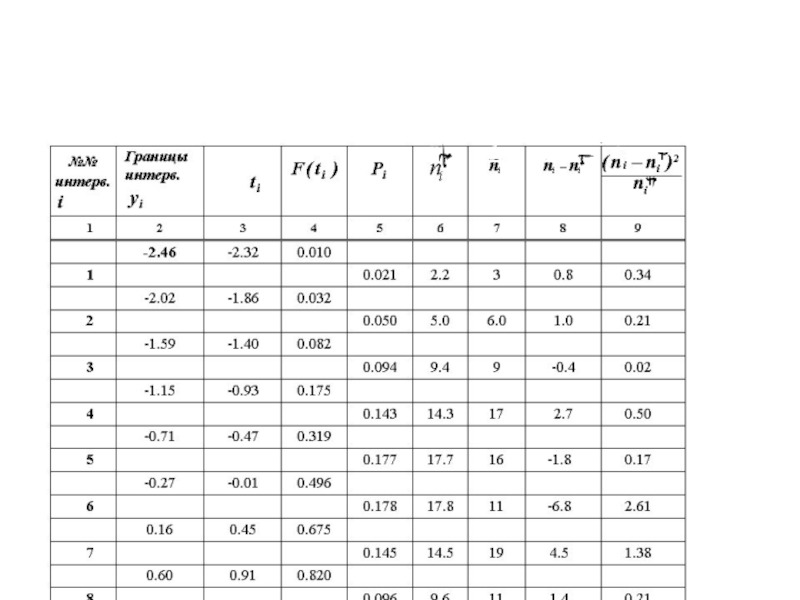
Слайд 18Пример. Проверить гипотезу о нормальности распределения
Слайд 19Решение
n = 100 – объем выборки;
xmax = 1.91 – максимальный
элемент выборки;
xmin = –2.46 – минимальный элемент выборки;
R =
4.37 – размах выборки;
Примем k = 10 – число интервалов.
Вычислим С = R/k =0.44 – длина интервала.
Слайд 20Числовые характеристики
Оценка математического ожидания (среднее выборочное)
= –0,266
Оценка среднего квадратического отклонения:
S = 0,95;
Слайд 21
Вероятность Pi=P находится с помощью функции распределения:
Слайд 25
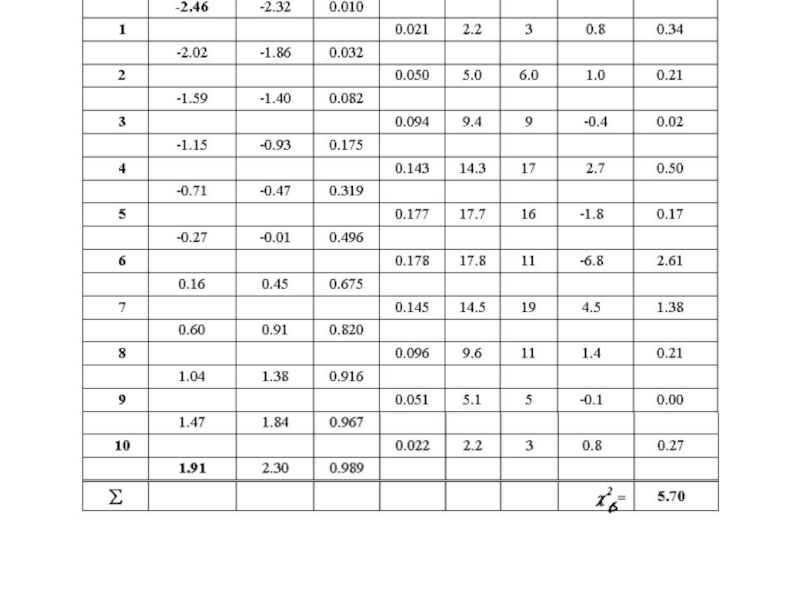
5,70 – эмпирическое значение критерия согласия Пирсона ( критерия χ2);
14,07
– критическое значение критерия Пирсона, полученное для доверительной вероятности 1
–α = 0.95 (т.е. на уровне значимости α = 0.05 = 5%) и числа степеней свободы ν = k – 3 = 7 из таблицы.
Слайд 27χв2 = 5,70< 14,07= χкр.2
Анализ результатов проверки статистических гипотез
позволяет сделать вывод о том, что гипотеза о нормальном распределении
не отвергается.
Генеральную совокупность можно моделировать с помощью нормального закона распределения с параметрами:
a= 0.27,
σ = 0.95.