Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прямая линия Прямая в пространстве бесконечна и непрерывна. Ограниченная часть
Содержание
- 1. Прямая линия Прямая в пространстве бесконечна и непрерывна. Ограниченная часть
- 2. XА2А1В1В2XА2А1b2 Иb1 ИЭпюром прямой называется чертеж, состоящий
- 3. Определение длины отрезка прямой линии и углов наклона прямой к плоскостям проекций
- 4. ПiПjXi,jAjAiВjBBiA////jiНатуральная величина отрезка прямойСпособ прямоугольного треугольникаДано: [АВ]
- 5. ПiПjXi,jAjAiВjBBiABIBIjkBkAkABkAB//////////// //// ////////zzjiC CiпппkAkAпAiBiпkAДоказательство:АВI ll AiBi;
- 6. A1B1A2B2B0A0zABzABнв АBнв АBх[АВ] – натуральная величина (гипотенуза)α
- 7. A1B1A2C2B2B0A0нв АBнв АBхС≡С1N≡N2N1С – горизонтальный след прямой АВN – фронтальный след прямой АВСледы прямой
- 8. Положение прямой относительно плоскостей проекций
- 9. Слайд 9
- 10. Прямая общего положения произвольно расположена в
- 11. Линии уровня
- 12. Линией уровня называется линия, параллельная одной из
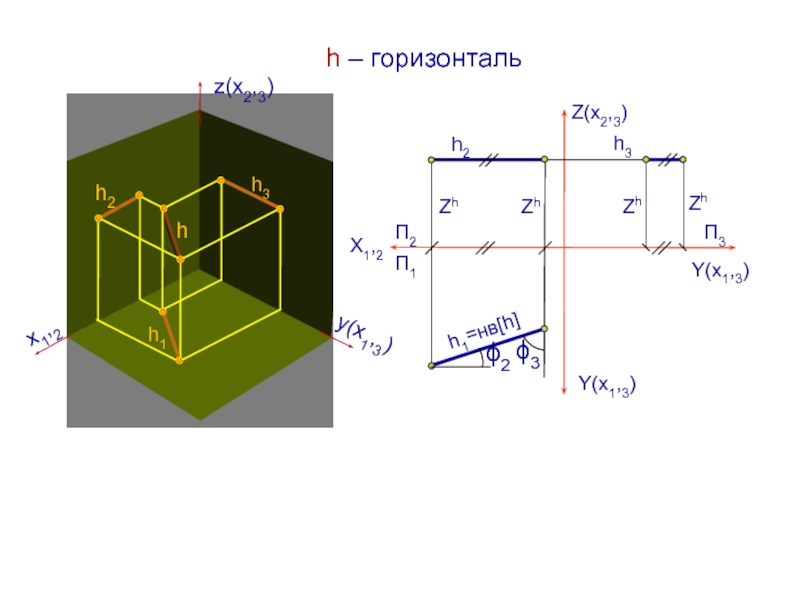
- 13. h2h3h1=нвhП1П2Х1,2ZhZhZhZhП3Z(х2,3)Y(х1,3)Y(х1,3)h – горизонталь3 2 h2h1h3hz(х2,3)y(х1,3)x1,2
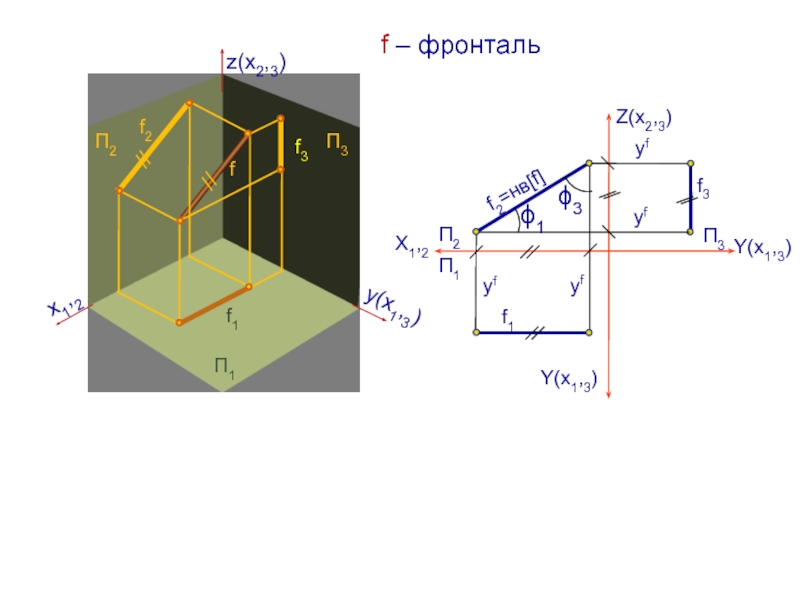
- 14. f1f2=нвfХ1,2yfП3Z(х2,3)Y(х1,3)f – фронталь yfyfyff31 3 Y(х1,3)П2П1f3f1f2fx1,2y(х1,3)z(х2,3)П3П2П1////
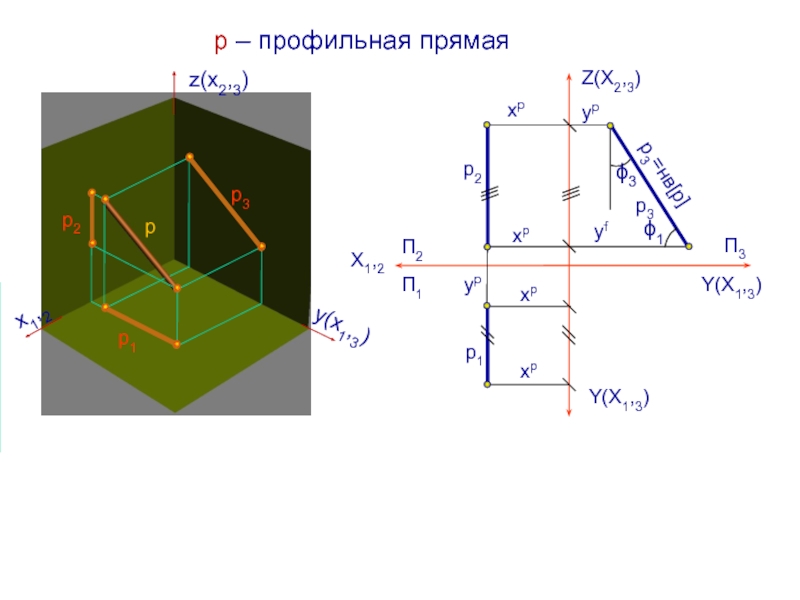
- 15. р – профильная прямаяр1р3=нврХ1,2П3Z(Х2,3)Y(Х1,3)yfyрр31 3 Y(Х1,3)р2хрхрП2П1хрхрyрр2р3р1рz(х2,3)y(х1,3)x1,2
- 16. Проецирующей называется прямая, перпендикулярная какой-либо плоскости проекций:
- 17. а – горизонтально проецирующая прямаяв – фронтально проецирующая прямаяс – профильно проецирующая прямаяХ1,2П3Z(Х2,3)Y(Х1,3)Y(Х1,3)П2П1а2а1а3b2b3b1c2c1c3
- 18. Взаимное расположение двух прямых
- 19. Пересекающиеся прямые (a ∩ b = K)
- 20. если одноименные проекции прямых на каждой из
- 21. Скрещивающиеся прямые признак основан на невыполнении
- 22. Дано: АВ ВС; АВ ll Пi;
- 23. Слайд 23
- 24. Преобразование комплексного чертежа
- 25. Способ замены плоскостей проекций
- 26. Геометрический объект в пространстве остается неподвижным, изменяет положение аппарат проецирования
- 27. А2А1П2П1Х1,2АХ1,2П1П4Х1,4АХ1,4А4sszAzAЗаменяемая плоскостьРабочая плоскостьНовая плоскостьssssss
- 28. х////Натуральная величина////Натуральная величинаВновь вводимая плоскость должна быть
- 29. П2П1Х1,2П4Х1,4А2В2С2В1С1А1В4А4С4П1h2h1Задача Преобразовать плоскость общего положения в проецирующую
- 30. П2П1П2П5Х5,2Х2,1новая плоскость П5 ll следу плоскости В2С2В1С1А1А2А5В5С5////нвПреобразовать проецирующую плоскость в плоскость уровняЗадача
- 31. задачи, которые можно решить методомзамены плоскостей проекций
- 32. 1. Определение натуральной величины отрезка2. Определение расстояния
- 33. 6. Определение расстояния от точки до плоскости(плоскость
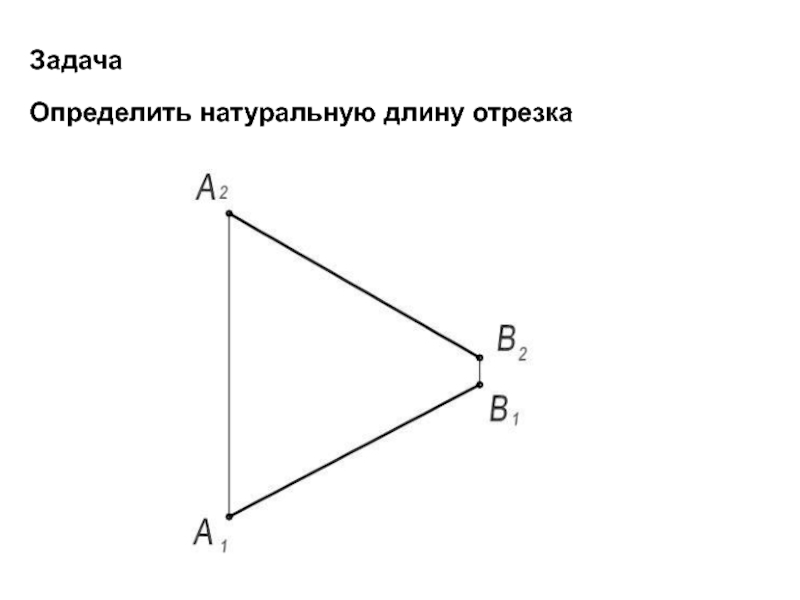
- 34. ЗадачаОпределить натуральную длину отрезка
- 35. Скачать презентанцию
XА2А1В1В2XА2А1b2 Иb1 ИЭпюром прямой называется чертеж, состоящий из двух или более ортогональных проекций, связанных между собойСпособы задания прямой на эпюре:Проекциями двух принадлежащих ей точекПроекцией точки и направлением
Слайды и текст этой презентации
Слайд 1
Прямая линия
Прямая в пространстве бесконечна и непрерывна.
Ограниченная часть прямой
называется отрезком.
Слайд 2X
А2
А1
В1
В2
X
А2
А1
b2 И
b1 И
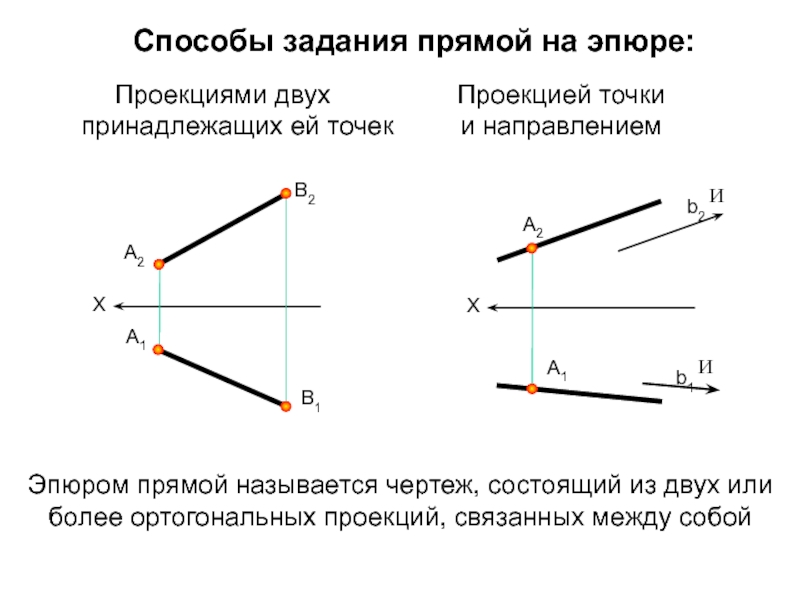
Эпюром прямой называется чертеж, состоящий из двух или
более ортогональных проекций, связанных между собой
Способы задания прямой на эпюре:
Проекциями
двух принадлежащих ей точекПроекцией точки
и направлением
Слайд 4Пi
Пj
Xi,j
Aj
Ai
Вj
B
Bi
A
//
//
ji
Натуральная величина отрезка прямой
Способ прямоугольного треугольника
Дано:
[АВ] ; [АiBi]; [AjBj]
Теорема:
Натуральная
величина отрезка АВ есть гипотенуза прямоугольного треугольника, у которого один
катет есть его проекция, а другой катет - разность координат концов этого отрезка (взятый из другой проекции).Угол между проекцией АiВi
и гипотенузой (натуральной величиной АВ ) равен углу оi наклона отрезка АВ к плоскости П i и к проекции АiВi
![ПiПjXi,jAjAiВjBBiA////jiНатуральная величина отрезка прямойСпособ прямоугольного треугольникаДано: [АВ] ; [АiBi]; [AjBj]Теорема:Натуральная величина отрезка АВ есть гипотенуза прямоугольного треугольника,](/img/thumbs/33a042cf8b8f0b06981f341217523bee-800x.jpg "Прямая линия
Прямая в пространстве бесконечна и непрерывна. Ограниченная часть ПiПjXi,jAjAiВjBBiA////jiНатуральная величина отрезка прямойСпособ прямоугольного треугольникаДано: [АВ] ; [АiBi]; [AjBj]Теорема:Натуральная величина")
Слайд 5Пi
Пj
Xi,j
Aj
Ai
Вj
B
Bi
A
BI
BIj
kB
kA
kAB
kAB
///
///
//
//
// //
// //
///
///
z
z
ji
C Ci
ппп
kA
kA
пAiBiп
kA
Доказательство:
АВI ll AiBi; BBI АВI
[АВ] –
натуральная величина (гипотенуза)
АВI= AiBi (1катет)
k = kB – kA =
Вj хi,j – Aj хi,jkA = ВiВI
kB = ВiВ
k = kB – kA = ВIВ
Р ВАВI = Р ВСBi
ji
![ПiПjXi,jAjAiВjBBiABIBIjkBkAkABkAB//////////// //// ////////zzjiC CiпппkAkAпAiBiпkAДоказательство:АВI ll AiBi; BBI АВI[АВ] – натуральная величина (гипотенуза)АВI= AiBi (1катет)k = kB](/img/thumbs/41b2abe36e703644c8f349285cb35a25-800x.jpg "Прямая линия
Прямая в пространстве бесконечна и непрерывна. Ограниченная часть ПiПjXi,jAjAiВjBBiABIBIjkBkAkABkAB//////////// //// ////////zzjiC CiпппkAkAпAiBiпkAДоказательство:АВI ll AiBi; BBI АВI[АВ] – натуральная величина")
Слайд 6A1
B1
A2
B2
B0
A0
zAB
zAB
нв АB
нв АB
х
[АВ] – натуральная величина (гипотенуза)
α - угол наклона
отрезка АВ
к плоскости П1
и к проекции А1В1
β -
угол наклона отрезка АВ к плоскости П2
и к проекции А2В2
![A1B1A2B2B0A0zABzABнв АBнв АBх[АВ] – натуральная величина (гипотенуза)α - угол наклона отрезка АВ к плоскости П1 и к](/img/thumbs/793eeeeaec0eb4abfd0a98f58570de25-800x.jpg "Прямая линия
Прямая в пространстве бесконечна и непрерывна. Ограниченная часть A1B1A2B2B0A0zABzABнв АBнв АBх[АВ] – натуральная величина (гипотенуза)α - угол наклона отрезка")
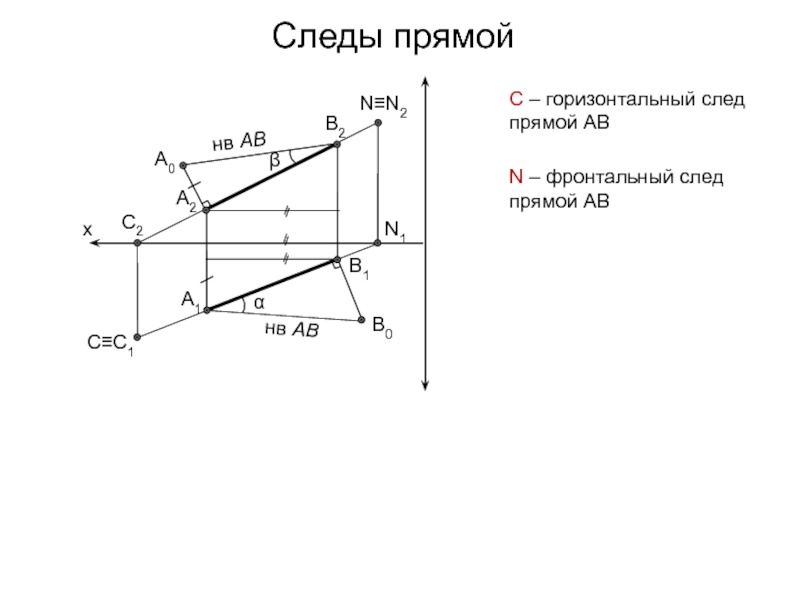
Слайд 7A1
B1
A2
C2
B2
B0
A0
нв АB
нв АB
х
С≡С1
N≡N2
N1
С – горизонтальный след прямой АВ
N – фронтальный
след прямой АВ
Следы прямой
Слайд 9
A1
B1
A
A2
Ax
B
B2
= 0; АВ||П1
A1
B1
A
A2
Ax
C
C2
0
B
B2
D
D2
C1≡D1
= 90o
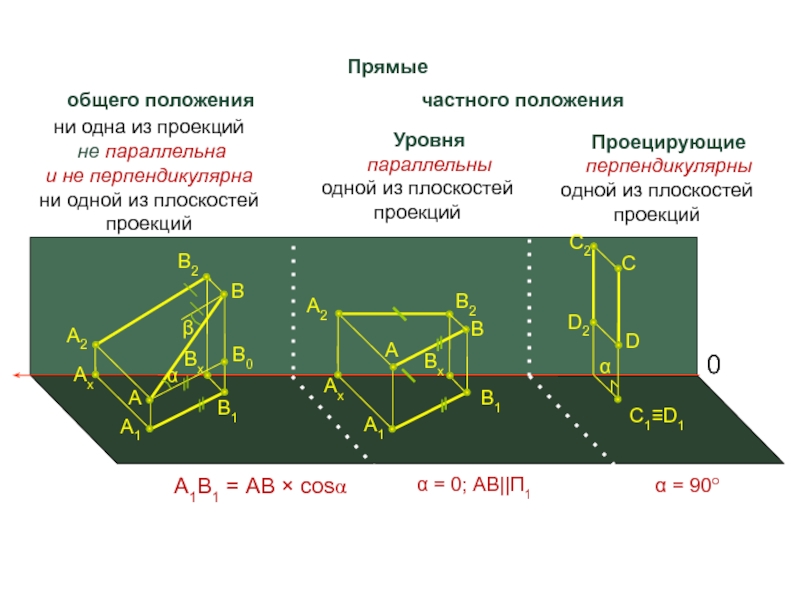
А1В1 = АВ
cosαПрямые
общего положения частного положения
Уровня
параллельны одной из плоскостей проекций
Проецирующие
перпендикулярны одной из плоскостей проекций
Вx
Вx
B0
ни одна из проекций
не параллельна
и не перпендикулярна
ни одной из плоскостей
проекций
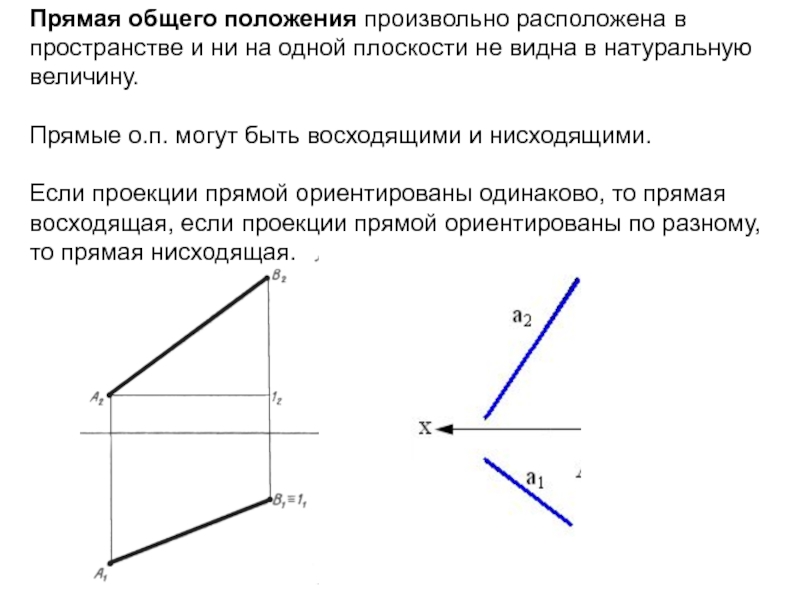
Слайд 10 Прямая общего положения произвольно расположена в пространстве и ни на
одной плоскости не видна в натуральную величину. Прямые о.п. могут быть
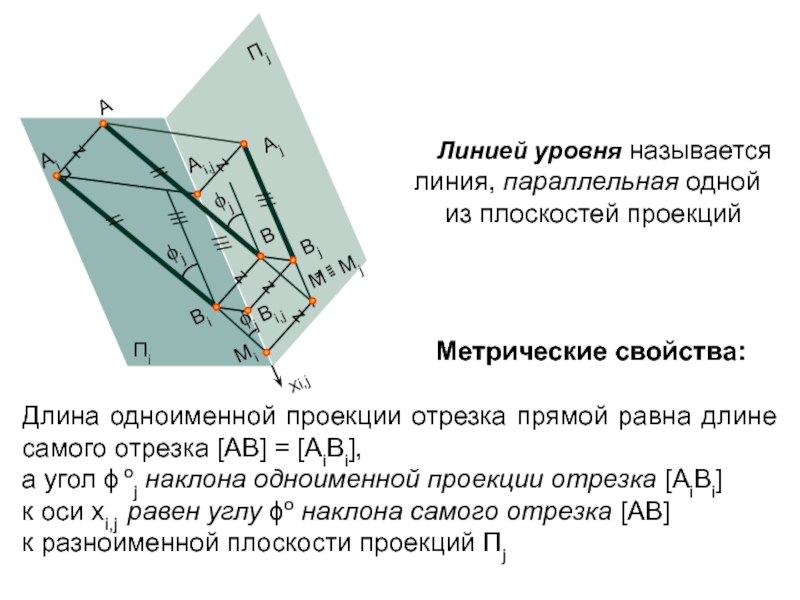
восходящими и нисходящими. Если проекции прямой ориентированы одинаково, то прямая восходящая, если проекции прямой ориентированы по разному, то прямая нисходящая.
Слайд 12Линией уровня называется линия, параллельная одной
из плоскостей проекций
Метрические
свойства:
Длина одноименной проекции отрезка прямой равна длине самого отрезка [АВ]
= [АiВi], а угол оj наклона одноименной проекции отрезка [АiВi]
к оси хi,j равен углу о наклона самого отрезка [АВ]
к разноименной плоскости проекций j
Пi
Пj
Xi,j
Aj
Ai
B
Bi
A
Bj
//
///
z
z
jj
М Мj
ппп
//
///
z
z
z
jj
///
jj
Мi
Bi,j
Ai,j
Слайд 13h2
h3
h1=нвh
П1
П2
Х1,2
Zh
Zh
Zh
Zh
П3
Z(х2,3)
Y(х1,3)
Y(х1,3)
h – горизонталь
3
2
h2
h1
h3
h
z(х2,3)
y(х1,3)
x1,2
Слайд 14f1
f2=нвf
Х1,2
yf
П3
Z(х2,3)
Y(х1,3)
f – фронталь
yf
yf
yf
f3
1
3
Y(х1,3)
П2
П1
f3
f1
f2
f
x1,2
y(х1,3)
z(х2,3)
П3
П2
П1
//
//
Слайд 15р – профильная прямая
р1
р3=нвр
Х1,2
П3
Z(Х2,3)
Y(Х1,3)
yf
yр
р3
1
3
Y(Х1,3)
р2
хр
хр
П2
П1
хр
хр
yр
р2
р3
р1
р
z(х2,3)
y(х1,3)
x1,2
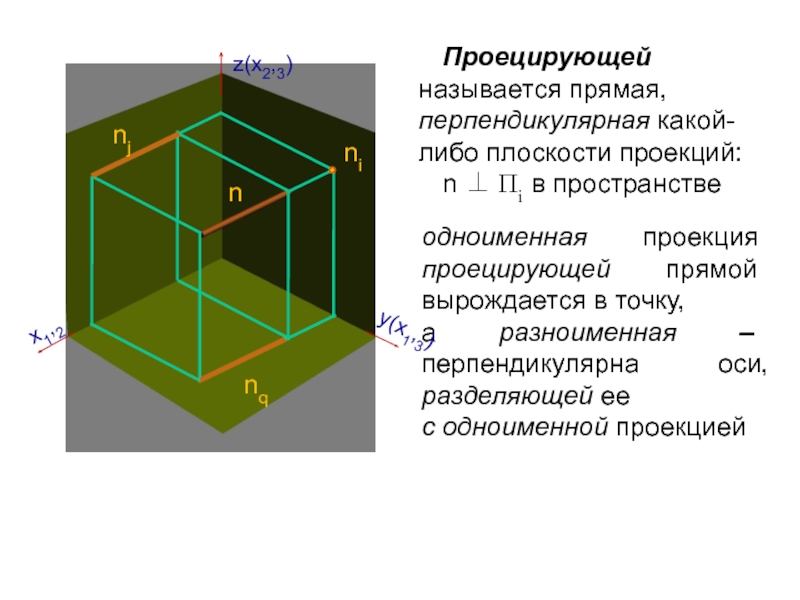
Слайд 16Проецирующей называется прямая, перпендикулярная какой-либо плоскости проекций:
n Пi
в пространстве
n
nj
ni
nq
одноименная проекция проецирующей прямой вырождается в точку,
а разноименная
– перпендикулярна оси, разделяющей ее с одноименной проекцией
x1,2
y(х1,3)
z(х2,3)
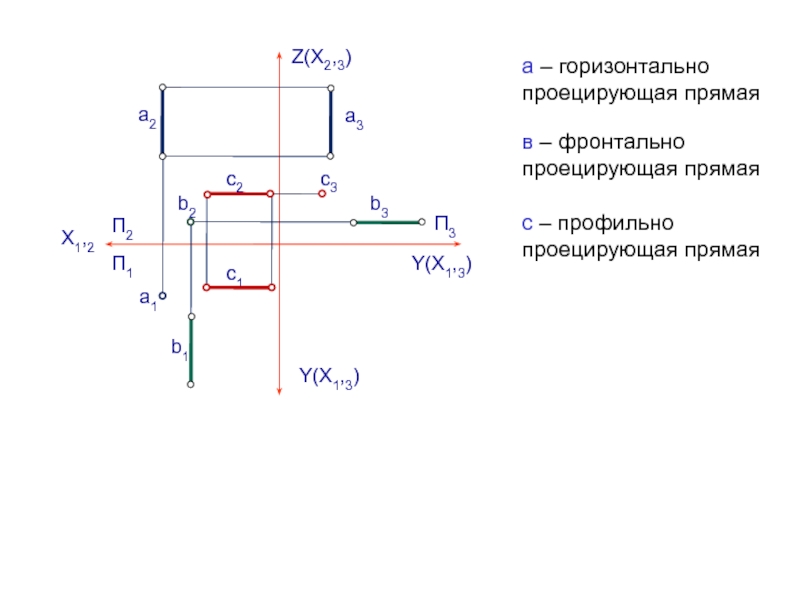
Слайд 17а – горизонтально проецирующая прямая
в – фронтально проецирующая прямая
с –
профильно проецирующая прямая
Х1,2
П3
Z(Х2,3)
Y(Х1,3)
Y(Х1,3)
П2
П1
а2
а1
а3
b2
b3
b1
c2
c1
c3
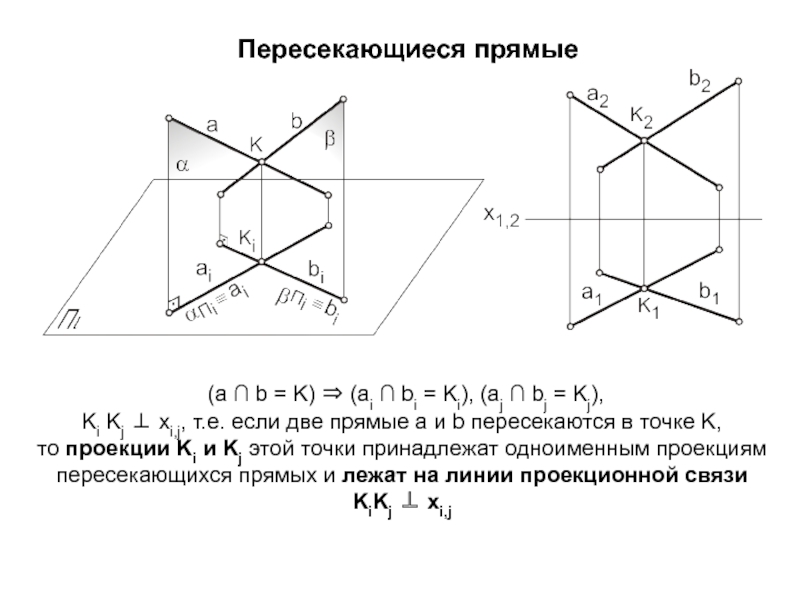
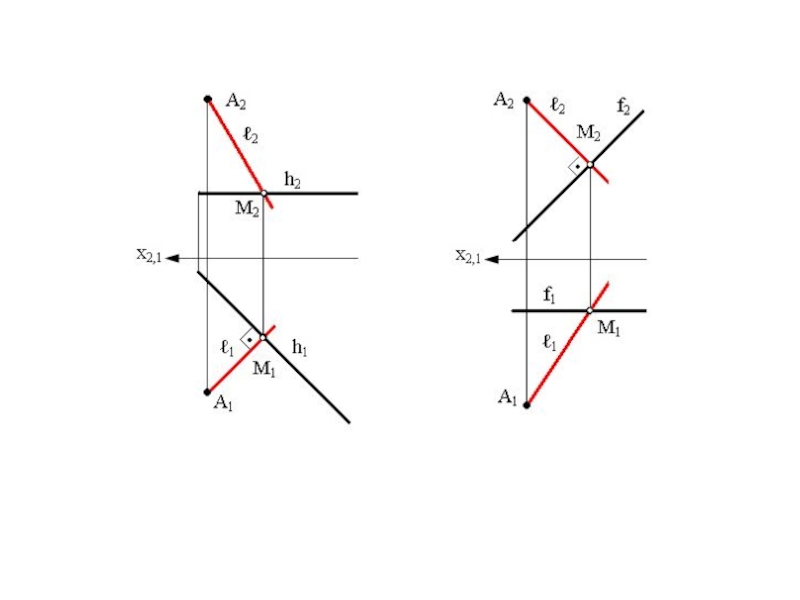
Слайд 19Пересекающиеся прямые
(a ∩ b = K) (ai ∩
bi = Ki), (aj ∩ bj = Kj),
Ki Kj
xi,j, т.е. если две прямые a и b пересекаются в точке K, то проекции Ki и Kj этой точки принадлежат одноименным проекциям пересекающихся прямых и лежат на линии проекционной связи KiKj xi,j
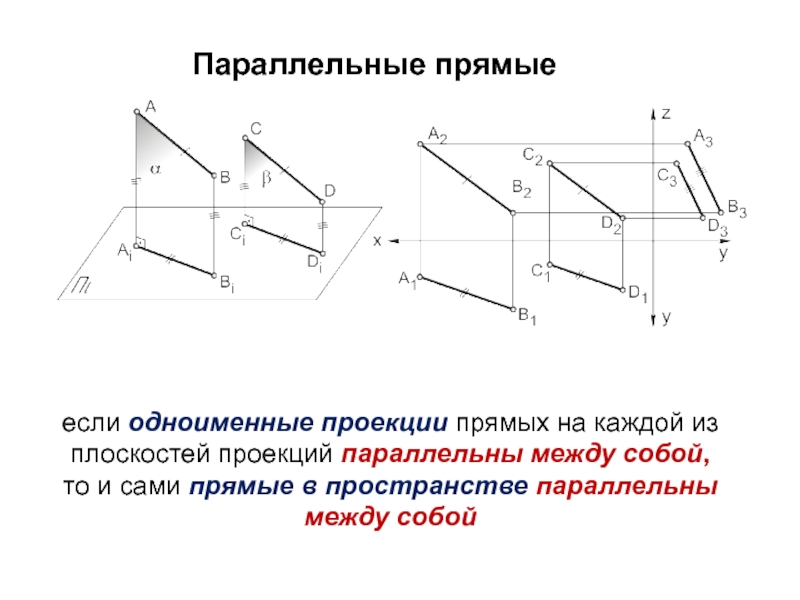
Слайд 20если одноименные проекции прямых на каждой из плоскостей проекций параллельны
между собой,
то и сами прямые в пространстве параллельны между
собой Параллельные прямые
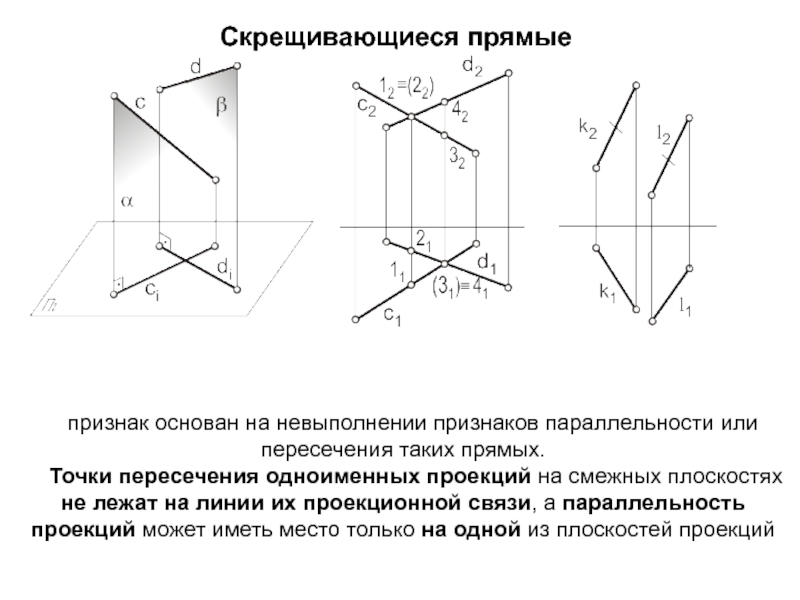
Слайд 21Скрещивающиеся прямые
признак основан на невыполнении признаков параллельности или
пересечения таких прямых.
Точки пересечения одноименных проекций на смежных плоскостях не
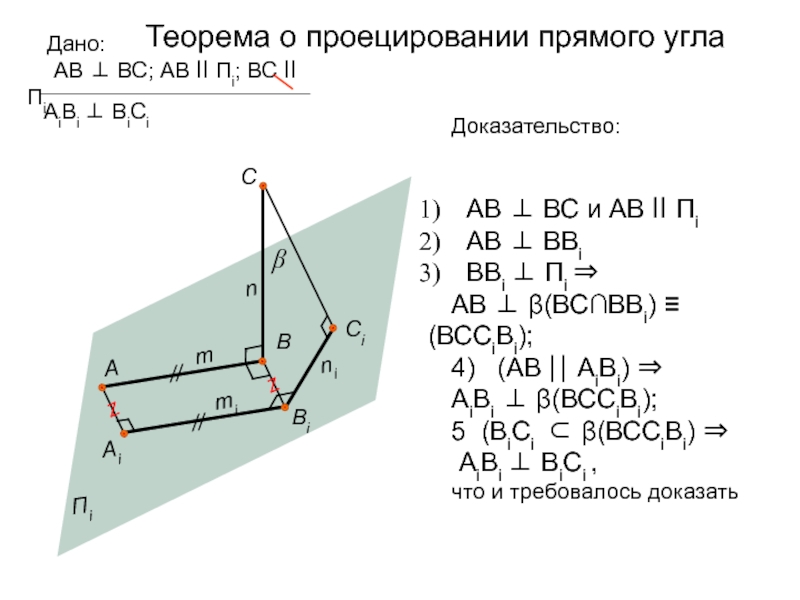
лежат на линии их проекционной связи, а параллельность проекций может иметь место только на одной из плоскостей проекций 
Слайд 22Дано:
АВ ВС; АВ ll Пi; ВС ll Пi
Доказательство:
АВ ВС и АВ ll Пi
АВ
ВВi ВВi Пi
АВ (ВС∩ВВi) (ВССiВi);
4) (АВ АiВi)
АiВi (ВССiВi);
5 (ВiСi (ВССiВi)
АiВi ВiСi ,
что и требовалось доказать
С
Аi
А
Вi
В
Сi
//
//
Z
Z
mi
m
n
ni
Пi
АiВi ВiСi
Теорема о проецировании прямого угла
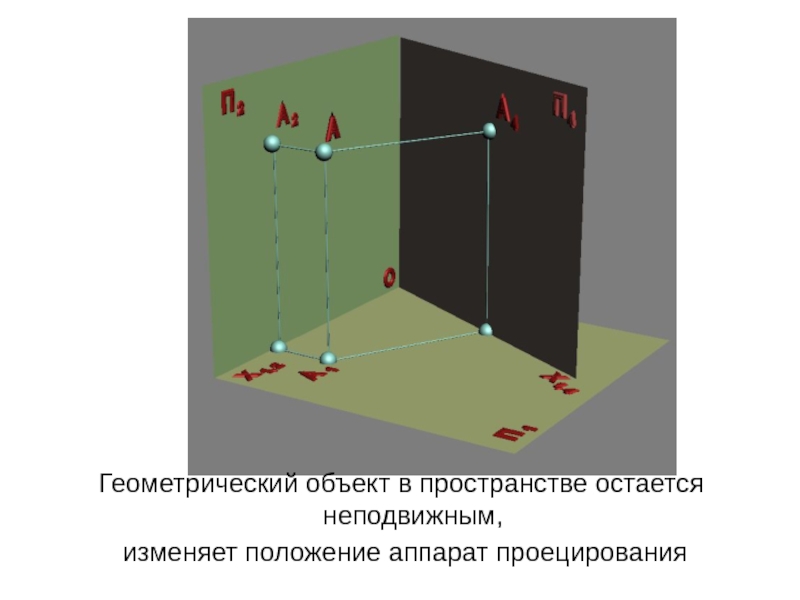
Слайд 26Геометрический объект в пространстве остается неподвижным,
изменяет положение аппарат проецирования
Слайд 27А2
А1
П2
П1
Х1,2
АХ1,2
П1
П4
Х1,4
АХ1,4
А4
s
s
zA
zA
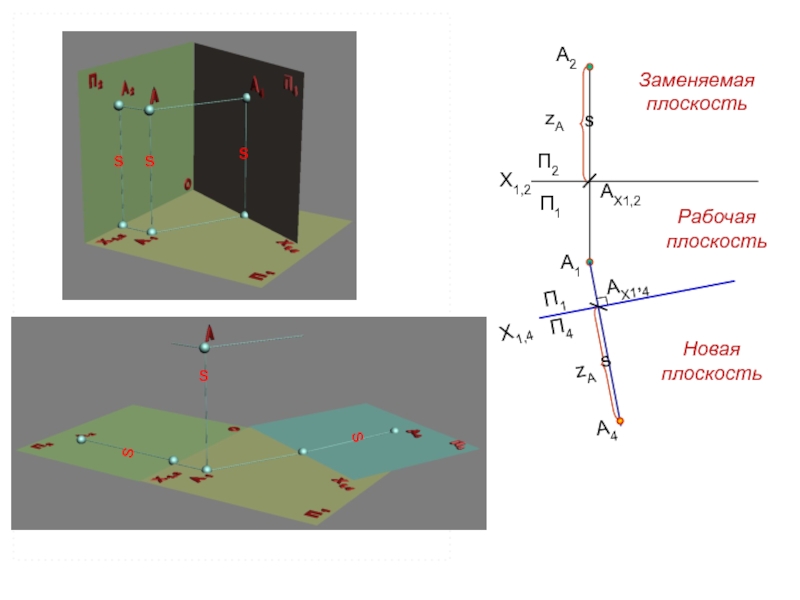
Заменяемая плоскость
Рабочая плоскость
Новая плоскость
s
s
s
s
s
s
Слайд 28х
//
//
Натуральная величина
//
//
Натуральная величина
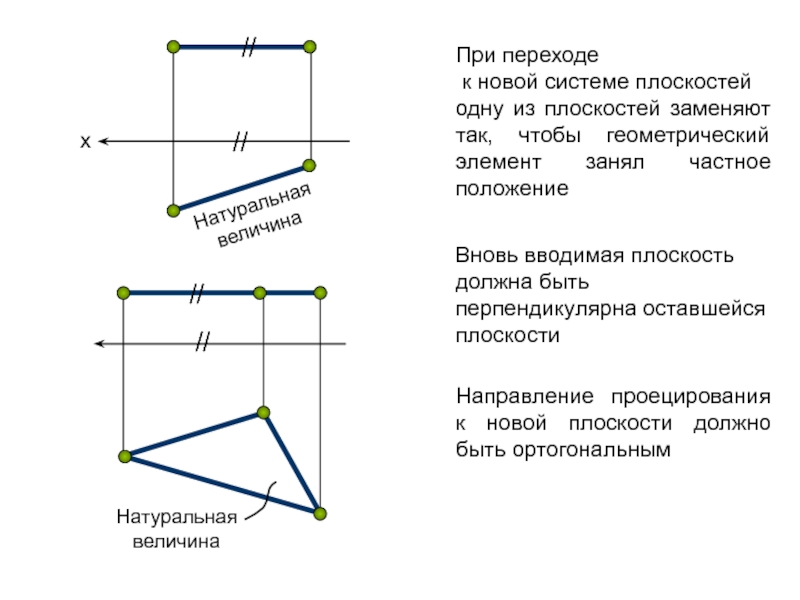
Вновь вводимая плоскость должна быть перпендикулярна оставшейся плоскости
При
переходе
к новой системе плоскостей
одну из плоскостей заменяют так,
чтобы геометрический элемент занял частное положениеНаправление проецирования к новой плоскости должно быть ортогональным
Слайд 29П2
П1
Х1,2
П4
Х1,4
А2
В2
С2
В1
С1
А1
В4
А4
С4
П1
h2
h1
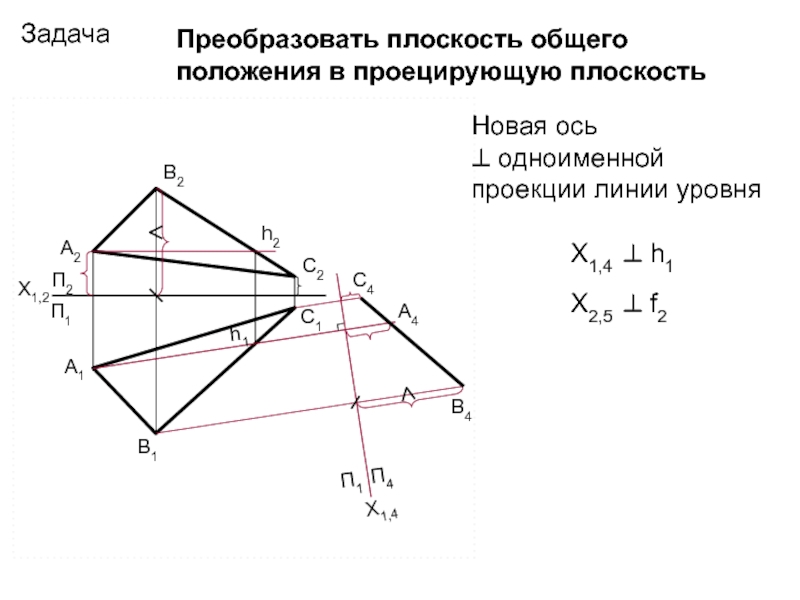
Задача
Преобразовать плоскость общего положения в проецирующую плоскость
Новая ось
^ одноименной
проекции линии уровня
Х1,4 ^ h1
Х2,5 ^ f2
Слайд 30П2
П1
П2
П5
Х5,2
Х2,1
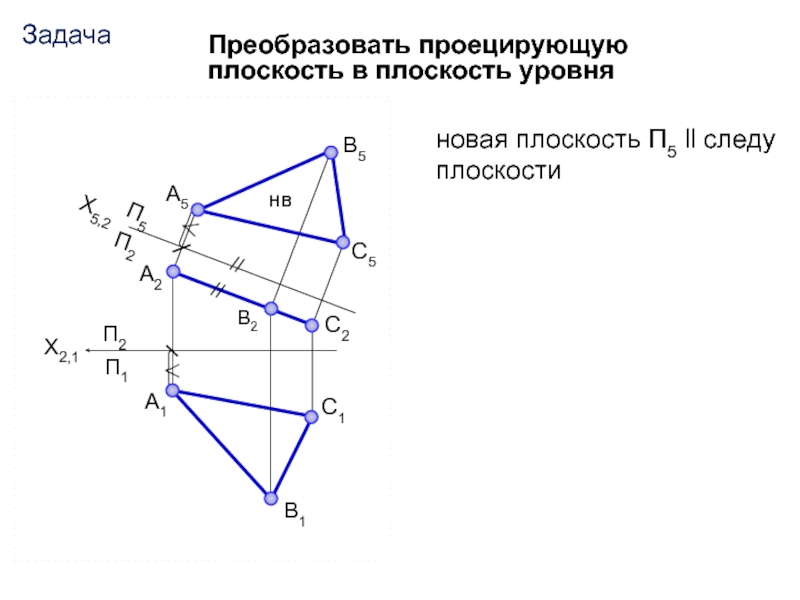
новая плоскость П5 ll следу
плоскости
В2
С2
В1
С1
А1
А2
А5
В5
С5
//
//
нв
Преобразовать проецирующую плоскость в плоскость
уровня
Задача
Слайд 321. Определение натуральной величины отрезка
2. Определение расстояния от точки до
прямой
(прямую преобразовать в проецирующую)
3. Определение расстояния между параллельными прямыми
(прямые преобразовать
в проецирующие)4. Определение величины двугранного угла
(общее ребро преобразовать в проецирующую прямую)
5. Определение расстояния между скрещивающими прямыми
(одну из прямых преобразовать в проецирующую)
Слайд 336. Определение расстояния от точки до плоскости
(плоскость преобразовать в след)
7.
Определение расстояния между параллельными плоскостями
(обе плоскости преобразовать в след)
Определение натуральной
величины плоской фигуры 9. Определение угла наклона прямой к плоскости
Определение угла наклона плоскости
к плоскостям проекций
