Расстояние от точки до прямой. Расстояние между параллельными прямыми

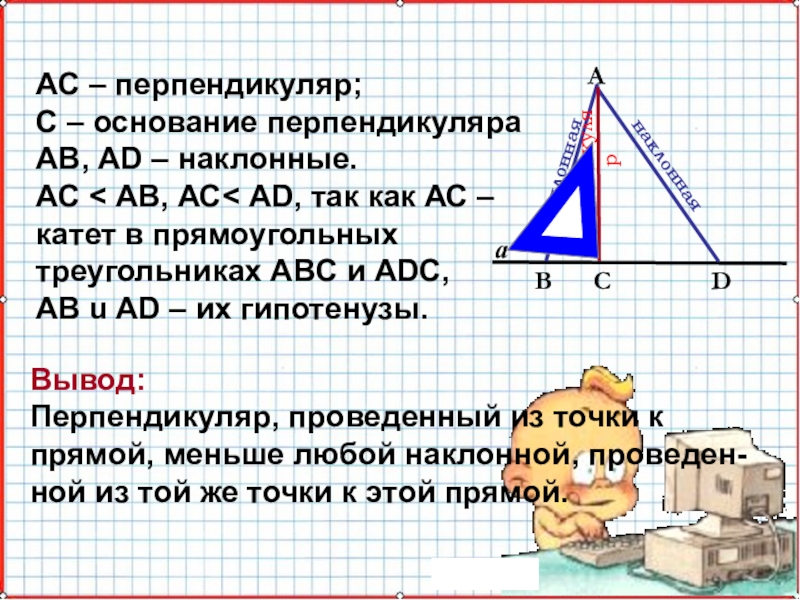
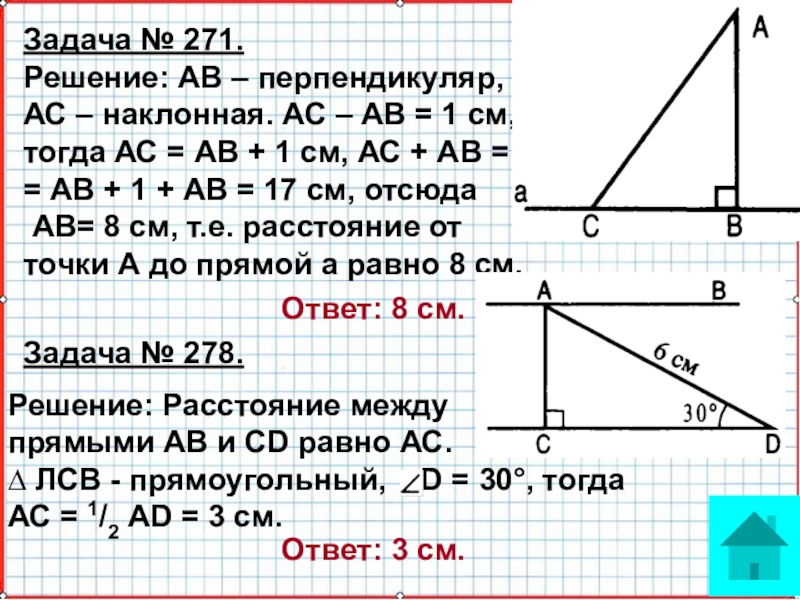
АС < АВ, АС< AD, так как АС – катет

в прямоугольных треугольниках ABC и ADC,
AB u AD – их гипотенузы.

Вывод:
Перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведен-ной из той же точки к этой прямой.

AH, проведенного из точки к прямой.
Расстояние от точки до прямой

– наименьшее из расстояний от этой точки до точек прямой.

Расстояние от точки до прямой

A

H

M

a

наклонная

прямой одинаково для всех точек.
Расстояние между параллельными прямыми
B
A
b
Если a ||

b, AB  b, MN  b (см. рис.), то AB = MN.

a

Если MN  b, то MN  a.

ΔABN = ΔNMA (по гипотенузе и острому углу)

Доказательство

Следовательно, AB = MN, ч.т.д.

Обратно: все точки по одну сторону от данной прямой, удаленные от нее на данное расстояние, лежат на параллельной прямой.

и равноудаленные
от нее, лежат на прямой, параллельной данной.

Пусть произвольные точки А и В распо-
ложены по одну сторону от прямой а и
расстояние от точки А до прямой а равно расстоянию от точки В до прямой а, т.е. АС= BD, где АС  a, BD  а.
Докажем, что АВ || а.
Доказательство: Так как АС  a и BD  а, то AC || BD, значит, накрест лежащие углы АСВ и CBD равны.
∆ АСВ = ∆ DBC по двум сторонам и углу между ними (АС = BD по условию теоремы, ВС- общая сторона, ACB= CBD как накрест лежащие при параллельных прямых АС и BD секущей ВС), следовательно, ABC= BCD.
ABC и BCD - накрест лежащие углы при прямых АВ и CD и секущей ВС и они равны, следовательно, АВ || CD, т.е. АВ || а, что и требовалось доказать.

из них до другой.
Расстояние между параллельными прямыми равно наименьшему из

расстояний от точек одной из них до точек другой: AB < MN.

Расстояние между параллельными прямыми

B

A

b

a

инструмента, называемого рейсмусом. Рейсмус используется в столярном деле для разметки

на поверхности деревянного бруска прямой, параллельной краю бруска. При передвижении рейсмуса вдоль края бруска металлическая игла прочерчивает отрезок прямой, параллельный краю бруска.

Продолжения высот АА1, ВВ1 и СС1 пересекаются в точке О.

Докажите, что ABC= AOC и
OAC= OBC.

прямая, перпендикулярная к АВ, пересекающая ВС в точке Е. ВС

= 24 см, периметр треугольника АЕС равен 30 см.
Найдите АС.

СЕ – CD=
= 3 см, тогда СЕ = CD

+ 3см, значит,
СЕ + CD = (CD+ 3) + CD=31 см,
откуда CD= 14см.
Расстояние от вершины С до прямой DE равно CD, т.е. 14 см.

Ответ: 14 см.

= 1 см,
тогда АС = АВ + 1 см, АС

+ АВ =
= АВ + 1 + АВ = 17 см, отсюда
АВ= 8 см, т.е. расстояние от
точки А до прямой а равно 8 см.

Решение: Расстояние между
прямыми АВ и CD равно АС.
∆ ЛСВ - прямоугольный, D = 30°, тогда
АС = 1/2 АD = 3 см.

Задача № 278.

Задача № 271.

Ответ: 3 см.

Ответ: 8 см.

расстояние от концов от-
резка АВ до прямой a (AD а,
ВС

a). ∆ AOD = ∆ ВОС по гипотенузе и острому углу (АО = OB, AOD = ВОС как вертикальные), тогда AD = СВ, то есть концы отрезка АВ равноудалены от прямой а.

Задача № 276.

АВС - равнобедренный, тогда
А = В.

∆ ЕМА = ∆ КМВ по катету
и прилежащему к нему острому
углу (ME = МК, ЕМА = КМВ.
Так как ЕМА = 90° – А =
= 90° – В = AMВ), тогда АМ = MB и СМ – медиана, проведенная из вершины равнобедренного треугольника к его основанию, а значит, и его высота.

Задача № 275.