Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Раздел 4. Элементы комбинаторики и теории вероятностей Тема: Решение задач
Содержание
- 1. Раздел 4. Элементы комбинаторики и теории вероятностей Тема: Решение задач
- 2. Повторение
- 3. Определение: Перестановкой из n элементов называется любое
- 4. РАЗМЕЩЕНИЯОпределение. Размещением из n элементов по m называется любое
- 5. СОЧЕТАНИЯОпределение. Сочетанием без повторений из n
- 6. Учитывается ли порядок следования элементов в соединении?Д АНЕТВсе ли элементы входят в соединение?СОЧЕТАНИЯРАЗМЕЩЕНИЯПЕРЕСТАНОВКИРn = n!Д АНЕТ
- 7. Задача1. В соревнованиях участвует 10 человек, трое
- 8. Решение задачи 11. В соревнованиях участвует 10
- 9. Решение задачи 12. В хирургическом отделении работают
- 10. Задача 3. Сколько пятизначных чисел можно составить
- 11. Решение задачи 3Рn= 5!=1*2*3*4*5=120 чисел Задача 3.
- 12. Решение задачи 4Рn= 10!=1*2*3*4*5*6*7*8*9*10=3 628 800 способов 4. Сколько существует способоврасстановки 10 книг на полке?
- 13. Подготовка к практической работе №2 Задача 5.
- 14. 6. Учащимся дали список из 10 книг,
- 15. 5. В группе 20 студентов . Сколькими
- 16. Задача №7 . В поисковой группе 6
- 17. Решение задачи №7Определим количество отрядов по 2
- 18. ПРАВИЛО СУММИРОВАНИЯ Если два взаимоисключающие действия могут быть
- 19. Практическая работа №2
- 20. Удачи!
- 21. Скачать презентанцию
Повторение
Слайды и текст этой презентации
Слайд 1Раздел 4. Элементы комбинаторики и теории вероятностей
Тема: Решение задач. Подготовка
к практической работе №2
Слайд 3
Определение: Перестановкой из n элементов называется любое упорядоченное множество из
n элементов.
Иными словами, это такое множество, для которого указано, какой
элемент находится на первом месте, какой – на втором, какой- на третьем, …, какой – на n-м месте. ПЕРЕСТАНОВКИ
Рn = n · (n - 1) · (n – 2) · … · 2 · 1 = n!
Слайд 4
РАЗМЕЩЕНИЯ
Определение. Размещением из n элементов по m называется любое упорядоченное множество из
m элементов, состоящее из элементов n элементного множества.
Слайд 5
СОЧЕТАНИЯ
Определение. Сочетанием без повторений из n элементов по m
-называется любое m элементное подмножество n -элементного множества
Определение. Сочетанием с
повторениями из n элементов по m -называются такие соединения из «m» элементнов, которые отличаются друг от друга хотя бы одним элементом.
Слайд 6
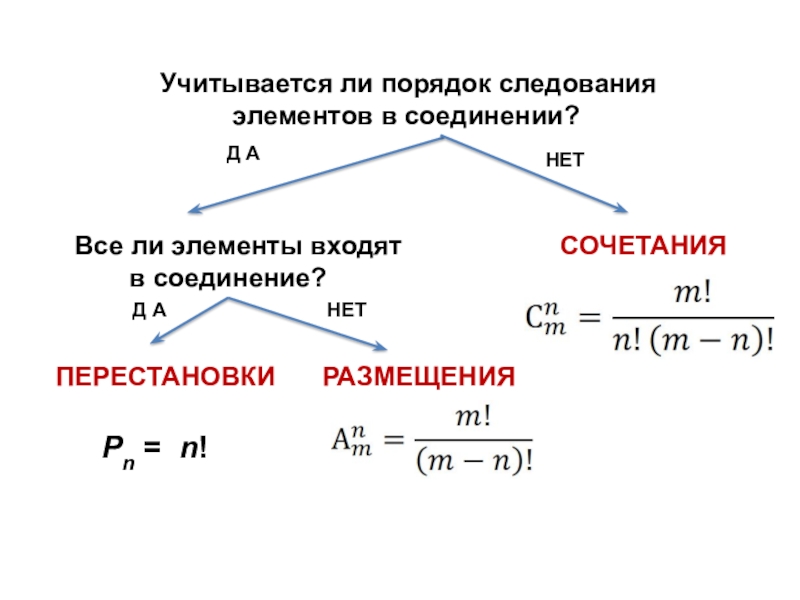
Учитывается ли порядок следования элементов в соединении?
Д А
НЕТ
Все ли элементы
входят в соединение?
СОЧЕТАНИЯ
РАЗМЕЩЕНИЯ
ПЕРЕСТАНОВКИ
Рn = n!
Д А
НЕТ
Слайд 7Задача1. В соревнованиях участвует 10 человек, трое из них займут
1-е, 2-е, и 3-е места. Сколько существует различных вариантов?
Подготовка к
практической работе №2 Задача 2. В хирургическом отделении работают 6 врачей. Сколькими способами из них можно образовать бригаду в составе хирурга и ассистента?
Слайд 8Решение задачи 1
1. В соревнованиях участвует 10 человек, трое из
них займут 1-е, 2-е, и 3-е места. Сколько существует различных
вариантов?
Слайд 9Решение задачи 1
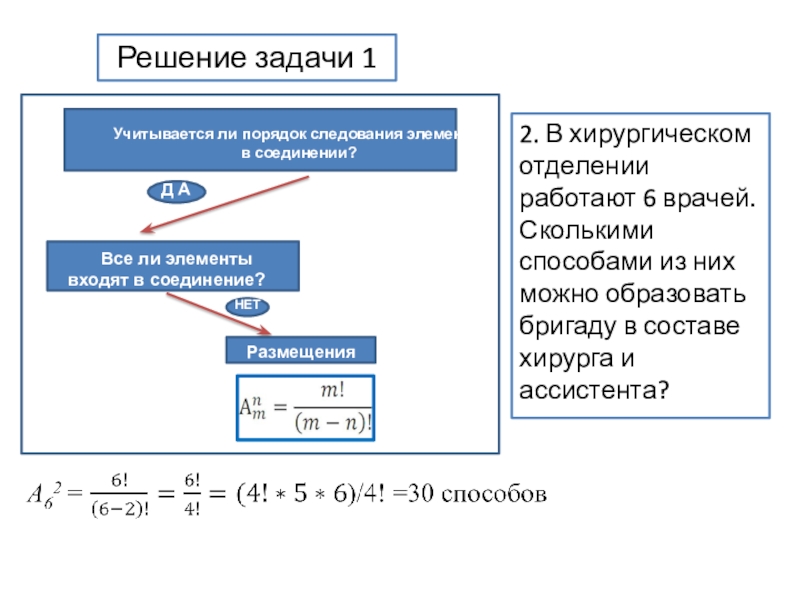
2. В хирургическом отделении работают 6 врачей. Сколькими
способами из них можно образовать бригаду в составе хирурга и
ассистента?
Слайд 10Задача 3. Сколько пятизначных чисел можно составить из цифр1,2,3,4,5, чтобы
ни в одна цифра в числе не повторялась?
Подготовка к практической
работе №2 Задача 4. Сколько существует способов
расстановки 10 книг на полке?
Слайд 11Решение задачи 3
Рn= 5!=1*2*3*4*5=120 чисел
Задача 3. Сколько пятизначных чисел
можно составить из цифр1,2,3,4,5, чтобы ни в одна цифра в
числе не повторялась?
Слайд 12Решение задачи 4
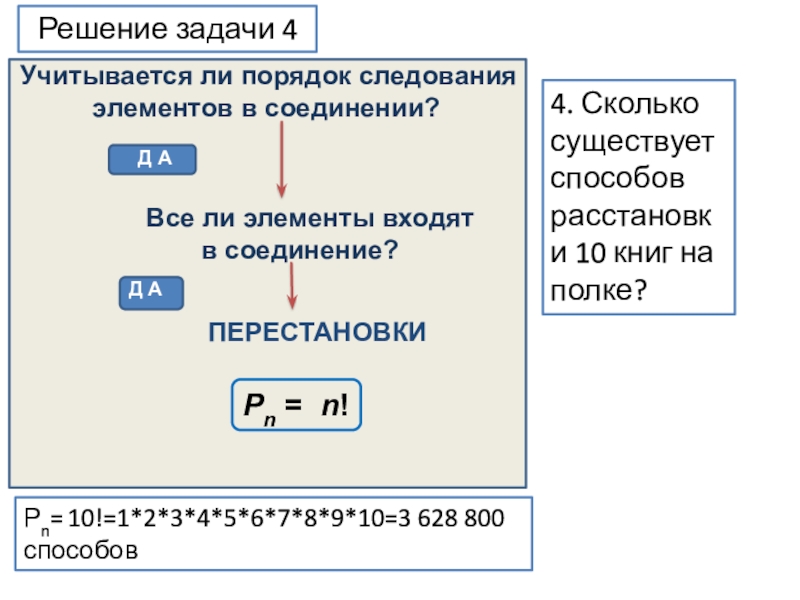
Рn= 10!=1*2*3*4*5*6*7*8*9*10=3 628 800 способов
4. Сколько существует
способов
расстановки 10 книг на полке?
Слайд 13Подготовка к практической работе №2
Задача 5. В группе 20
студентов . Сколькими способами можно из них выбрать 3 человека
для участия в конкурсе профессионального мастерства?Задача 6. Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг?
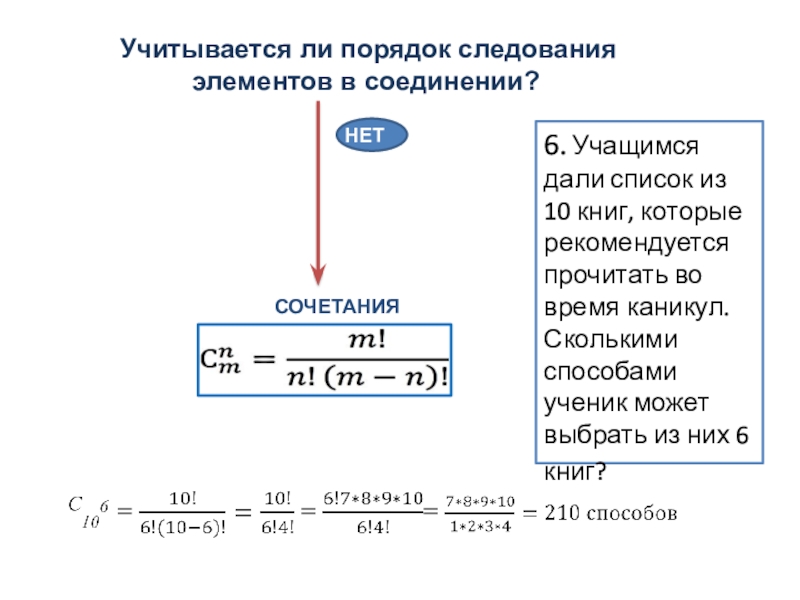
Слайд 146. Учащимся дали список из 10 книг, которые рекомендуется прочитать
во время каникул. Сколькими способами ученик может выбрать из них
6 книг?
Слайд 155. В группе 20 студентов . Сколькими способами можно из
них выбрать 3 человека для участия в конкурсе профессионального мастерства?
Слайд 16Задача №7 . В поисковой группе 6 человек. Для поисков
группа разбивается на отряды, но так, чтобы, в них было
не менее двух человек и не более 5 человек. Сколько различных отрядов можно организовать ?Подготовка к практической работе №2
Слайд 17Решение задачи №7
Определим количество отрядов по 2 человека:
С62 =15
(*проверить самостоятельно)
Определим количество отрядов по 3 человека
С63=20 (*проверить
самостоятельно) Определим количество отрядов по 4 человека
С64=15 (*проверить самостоятельно)
Определим количество отрядов по 5 человек
С65=6 (*проверить самостоятельно)
Общее число отрядов по правилу суммы будет равно : 15+20+15+6=56
Ответ: можно образовать 56 различных отрядов
Слайд 18ПРАВИЛО СУММИРОВАНИЯ
Если два взаимоисключающие действия могут быть выполнены в соответствии
k и m способами, тогда какое-то одно из этих действий
можно выполнить k + m способами.
