Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
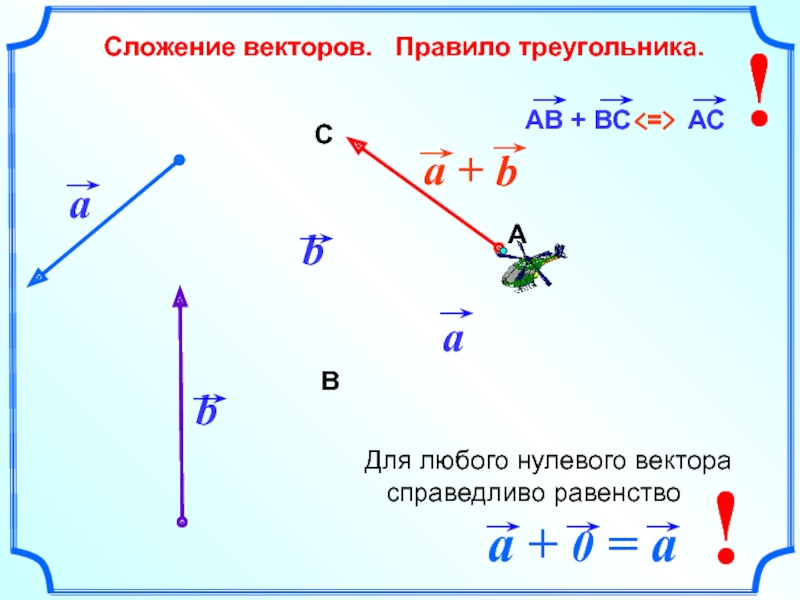
Сложение векторов. Правило треугольника. b b a b a + a А В С АВ + ВС = АС a + 0
Содержание
- 1. Сложение векторов. Правило треугольника. b b a b a + a А В С АВ + ВС = АС a + 0
- 2. В1 Докажем, что если при сложении
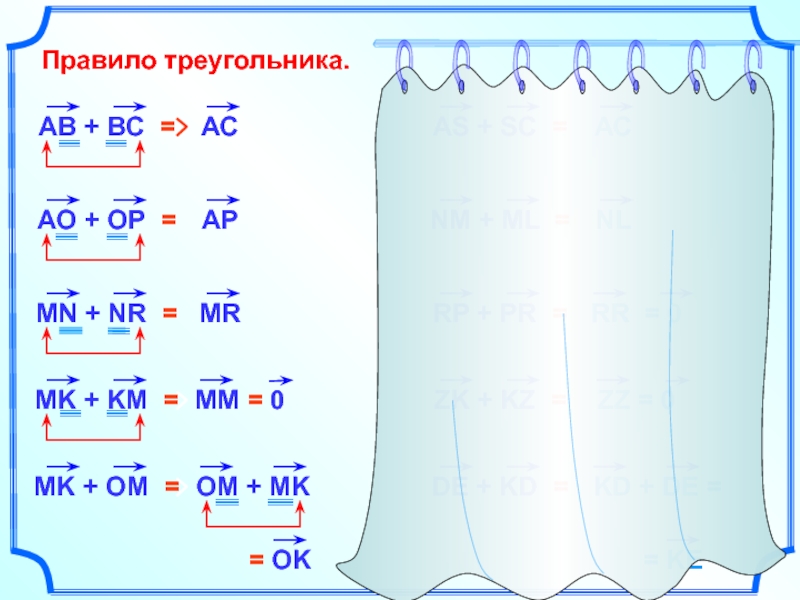
- 3. Правило треугольника.RR = 0
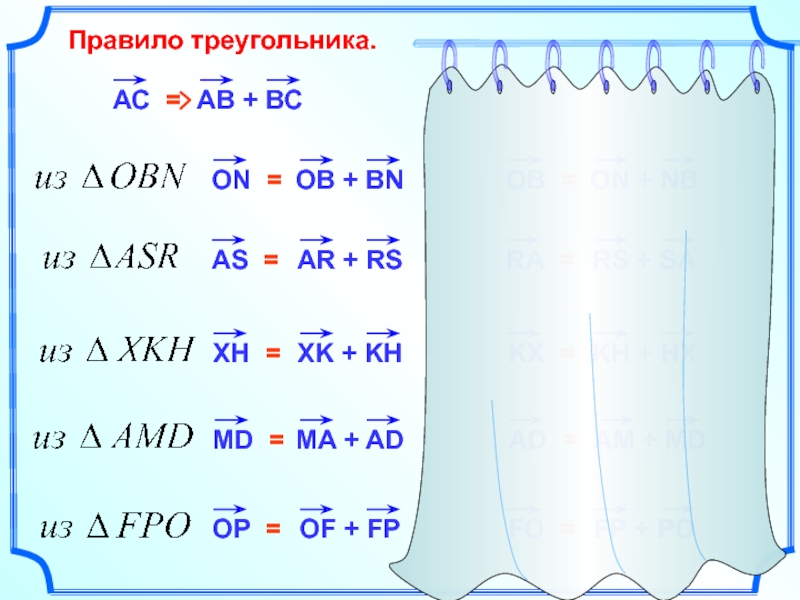
- 4. Правило треугольника.АС =OB =RA =KX =AD =FO =
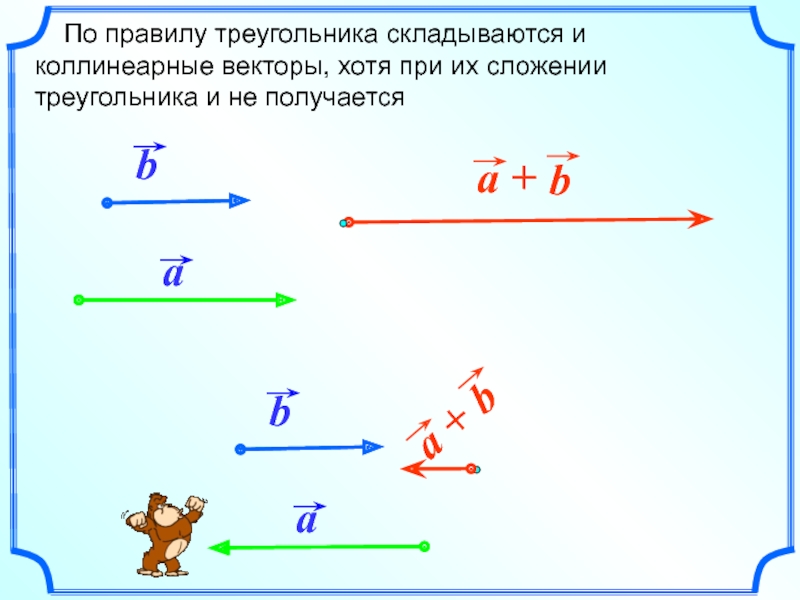
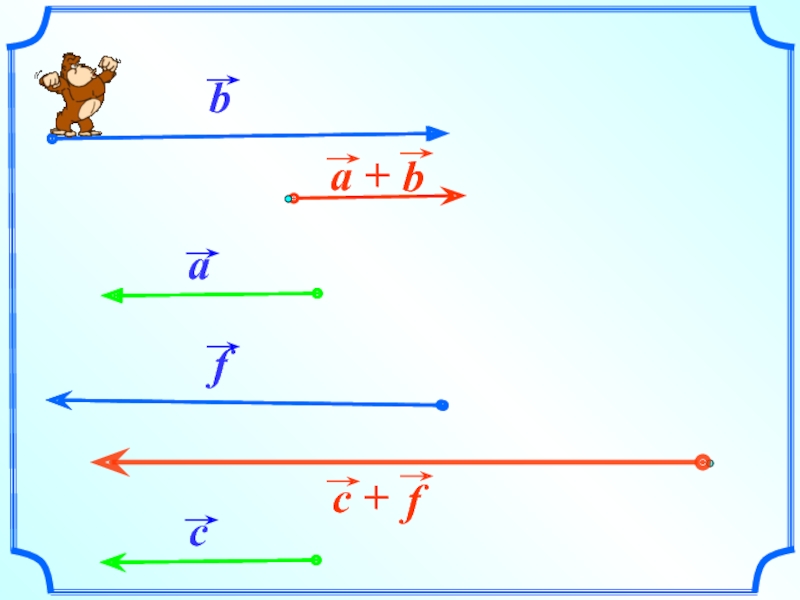
- 5. По правилу треугольника складываются и
- 6. Слайд 6
- 7. Законы сложения векторовДля любых векторов
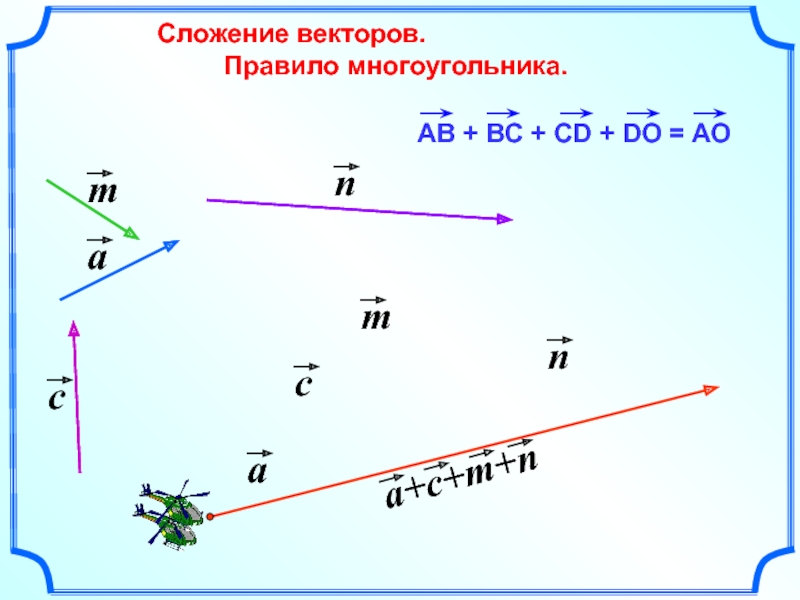
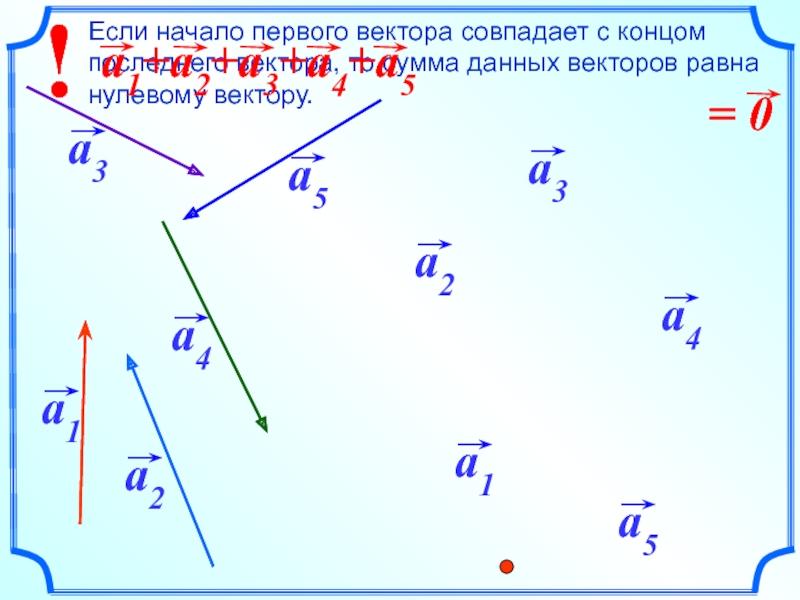
- 8. Сложение векторов. Правило многоугольника.
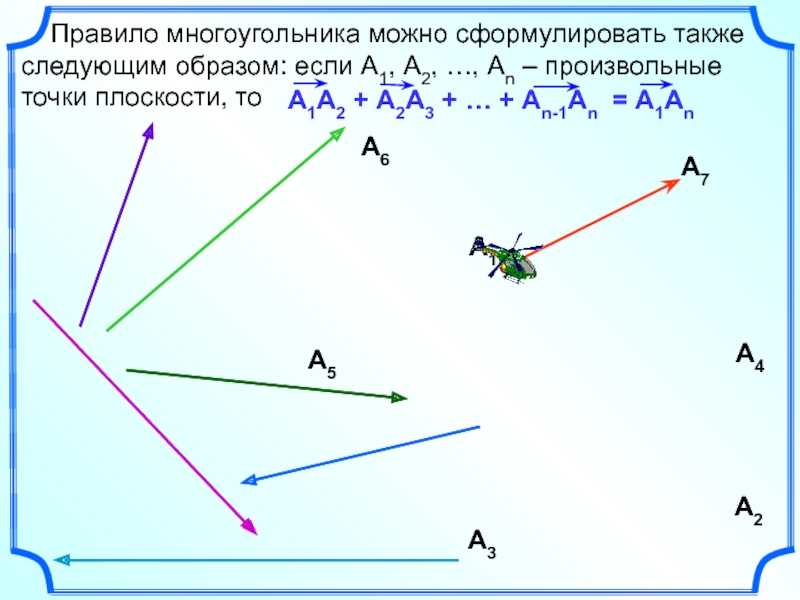
- 9. Правило многоугольника можно сформулировать также
- 10. Слайд 10
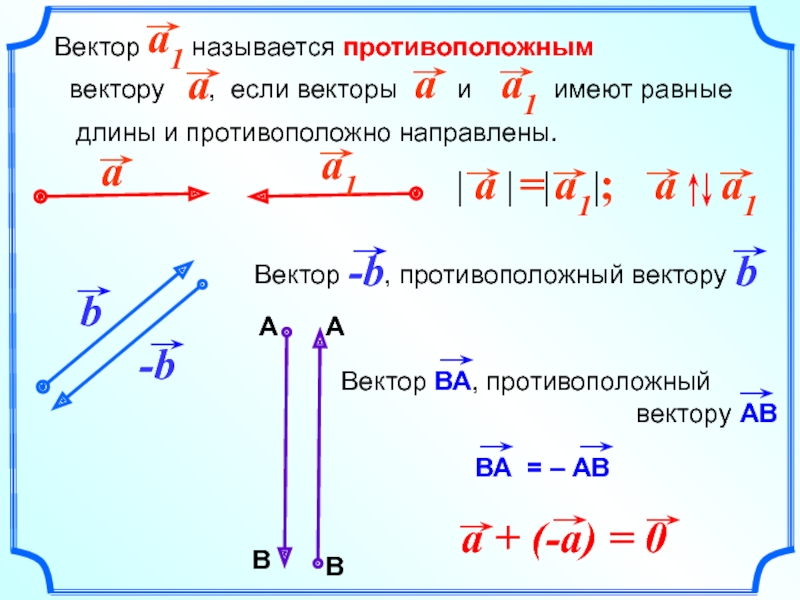
- 11. Вектор называется противоположным
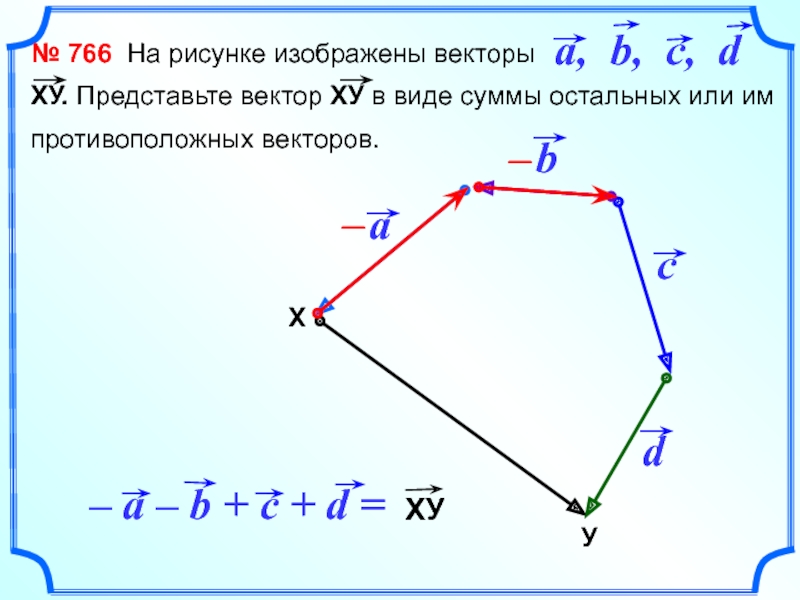
- 12. № 766 На рисунке изображены
- 13. Скачать презентанцию
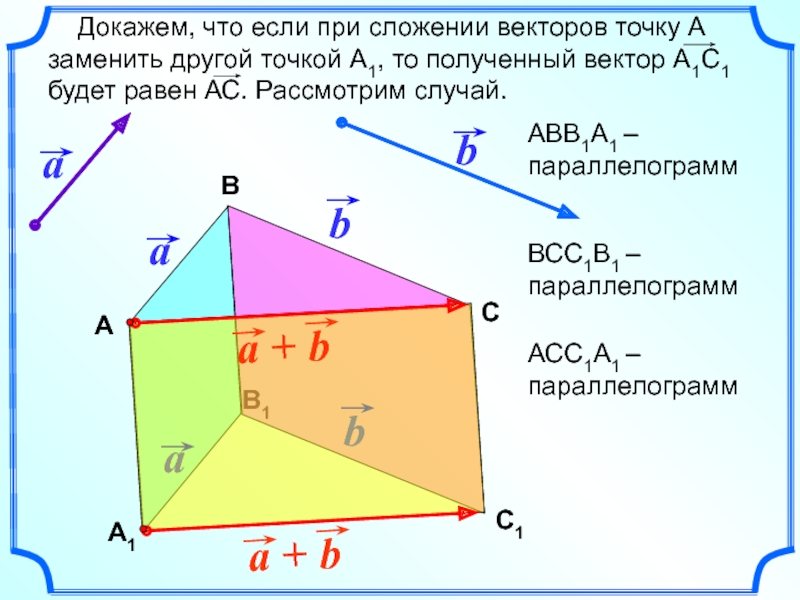
В1 Докажем, что если при сложении векторов точку А заменить другой точкой А1, то полученный вектор А1С1будет равен АС. Рассмотрим случай. ВСС1АВВ1А1 – параллелограмм ВСС1В1 – параллелограмм АСС1А1 – параллелограмм
Слайды и текст этой презентации
Слайд 1 Сложение векторов. Правило треугольника.
a
А
В
С
!
!
Для любого
нулевого вектора справедливо равенство
Слайд 2В1
Докажем, что если при сложении векторов точку А
заменить другой точкой А1, то полученный вектор А1С1
будет равен АС.
Рассмотрим случай. В
С
С1
АВВ1А1 – параллелограмм
ВСС1В1 – параллелограмм
АСС1А1 – параллелограмм
Слайд 5 По правилу треугольника складываются и коллинеарные векторы, хотя
при их сложении треугольника и не получается
Слайд 9 Правило многоугольника можно сформулировать также следующим образом: если
А1, А2, …, Аn – произвольные точки плоскости, то
= А1An
А1А2
+ А2А3 + … + Аn-1An А2
А3
А4
А5
А6
А7
А1
Слайд 11Вектор называется противоположным
вектору
, если векторы и
имеют равныедлины и противоположно направлены.
Слайд 12 № 766 На рисунке изображены векторы
ХУ.
Представьте вектор ХУ в виде суммы остальных или им
противоположных векторов.У
Х
–
–