Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Различные способы решения сложных неравенств задание С3
Содержание
- 1. Различные способы решения сложных неравенств задание С3
- 2. 1.2.3.метод интервалов для решения рациональных неравенствОсновные идеи решенияОТВЕТ
- 3. 1.2.Раскрытие модуля на промежуткахОсновные идеи решенияОТВЕТ
- 4. ОТВЕТОсновная проблема неравенстваОДЗ левой части b>0 и
- 5. ОТВЕТОсновная проблема неравенстваОДЗ левой части b>0 и
- 6. ОТВЕТ1.2.3.Одно из условий ОДЗ 0 <
- 7. ОТВЕТ1.2.3.«Мешанина» разных функций => надо разделить
- 8. ОТВЕТЧасто сложное неравенство сводится к уравнению с
- 9. Слайд 9
- 10. Скачать презентанцию
1.2.3.метод интервалов для решения рациональных неравенствОсновные идеи решенияОТВЕТ
Слайды и текст этой презентации
Слайд 1Различные способы решения «сложных» неравенств задание С3
По материалам
занятия мастер-класса Афанасьевой А.В. школа № 1580 г.Москвы
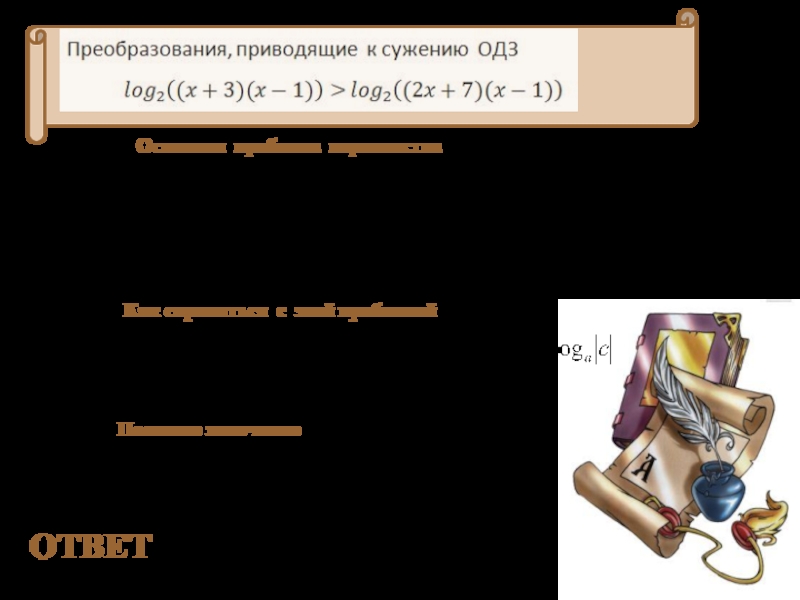
Слайд 4
ОТВЕТ
Основная проблема неравенства
ОДЗ левой части b>0 и c>0
ОДЗ правой части
bc>0
Переход СЛЕВА НАПРАВО расширяет ОДЗ
Переход СПРАВА НАЛЕВО сужает
ОДЗКак справиться с этой проблемой
Способ решения: переход к следствию (расширению ОДЗ) + пересечение с реальным ОДЗ
Слайд 5
ОТВЕТ
Основная проблема неравенства
ОДЗ левой части b>0 и c>0
ОДЗ правой части
bc>0
Переход СЛЕВА НАПРАВО расширяет ОДЗ
Переход СПРАВА НАЛЕВО сужает
ОДЗКак справиться с этой проблемой
Способ решения: переход к следствию + пересечение с реальным ОДЗ
Полезное замечание
При сравнении модулей выражений сравнивать их квадраты
Слайд 6
ОТВЕТ
1.
2.
3.
Одно из условий ОДЗ 0 < x < 6
=> одно из условий ОДЗ 0 < x/6
< 1=> «внешний» логарифм «снимается» однозначно
Некоторые советы
Избавиться от радикала можно заменой
При этом указать область изменения а
с учетом ОДЗ данного неравенства
НЕ ЗАБУДЬТЕ ВЕРНУТЬСЯ к х
В случае затруднения ВСПОМНИТЕ,
что есть другие способы решения:
Обобщенный метод интервалов
Метод замены множителей (метод рационализации)
Слайд 7
ОТВЕТ
1.
2.
3.
«Мешанина» разных функций => надо разделить (разложить на множители)
Внимательно
посмотрим на условие
Способ разложения: с помощью корней квадратного трехчлена
(Посмотрим на данное неравенство как на квадратное, относительно )Графический способ решения – полезная вещь
(для «мелких» уравнений)
Слайд 8
ОТВЕТ
Часто сложное неравенство сводится к уравнению с единственным корнем
Используем :
свойство
монотонности композиции функций
ограниченность функций
свойство суммы взаимно обратных функций
В случае затруднения ВСПОМНИТЕ,
что многие свойства функции поможет увидеть ее ПРОИЗВОДНАЯ
Теги
