Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
РЕГИСТРЫ и КОЛЬЦЕВЫЕ СЧЕТЧИКИ ДВОИЧНЫЕ СЧЕТЧИКИ и СЧЕТЧИКИ НА ИХ ОСНОВЕ
Содержание
- 1. РЕГИСТРЫ и КОЛЬЦЕВЫЕ СЧЕТЧИКИ ДВОИЧНЫЕ СЧЕТЧИКИ и СЧЕТЧИКИ НА ИХ ОСНОВЕ
- 2. ОСНОВНЫЕ ТЕМЫ ЛЕКЦИИСУММИРУЮЩИЙ СЧЕТЧИКВЫЧИТАЮЩИЙ СЧЕТЧИКРЕВЕРСИВНЫЙ СЧЕТЧИКСЧЕТЧИКИ С ПРОИЗВОЛЬНЫМ КОЭФФИ-ЦИЕНТОМ ДЕЛЕНИЯПАРАЛЛЕЛЬНЫЕ РЕГИСТРЫПОСЛЕДОВАТЕЛЬНЫЕ РЕГИСТРЫКОЛЬЦЕВЫЕ СЧЕТЧИКИ
- 3. ДВОИЧНЫЕ СЧЕТЧИКИ И СЧЕТЧИКИ НА ИХ ОСНОВЕ
- 4. ВЫЧИТАЮЩИЙ ДВОИЧНЫЙ СЧЕТЧИК На основе Т-триггеров можно
- 5. На рис. приведен фрагмент РЕВЕРСИВНОГО СЧЕТЧИ-КА. Этот
- 6. Общим недостатком всех счетчиков с последовательным переносом
- 7. СЧЕТЧИКИ С ПРОИЗВОЛЬНЫМ КОЭФФИЦИЕНТОМ ДЕЛЕНИЯ На практике часто
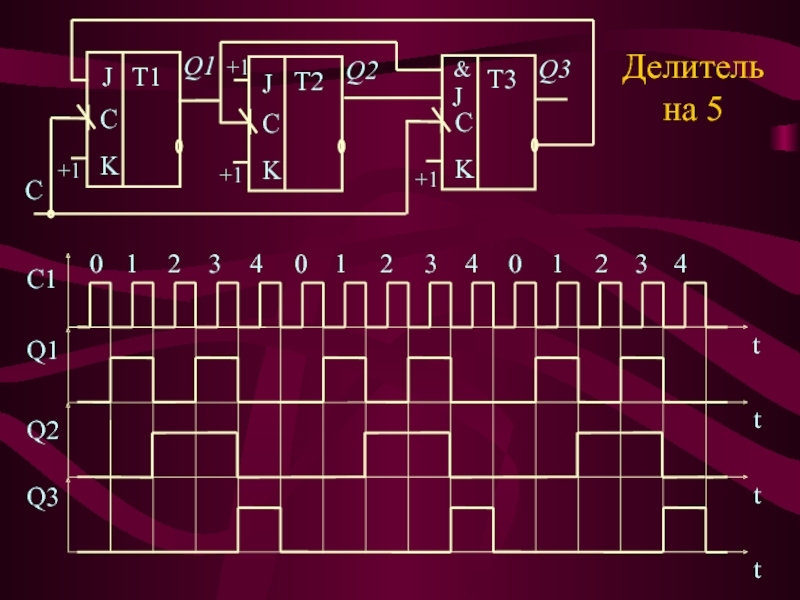
- 8. +1+1&+1JCQ1KCT1+1JQ2KCT2JQ3KCT3Делитель на 5С1Q1Q2Q3tttt102340123401234
- 9. Синтез делителя на k = 14 ⮚
- 10. Делитель реализован на D-триггерах типа КР1533ТМ2. Эти
- 11. При всех состояниях счетчика, кроме 12-го, на
- 12. После записи в триггер Т5 «нуля» устанавливаются
- 13. Слайд 13
- 14. Слайд 14
- 15. J-K-триггеры имеют только по одному входу J-
- 16. ПАРАЛЛЕЛЬНЫЕ И ПОСЛЕДОВАТЕЛЬНЫЕ РЕГИСТРЫ РЕГИСТРЫ
- 17. ПАРАЛЛЕЛЬНЫЕ РЕГИСТРЫ ПАРАЛЛЕЛЬНЫЕ РЕГИСТРЫ применяются для хранения
- 18. D2D1C1T1CDT2CDQ1Q2D4D3C2T3CDT4CDQ3Q4
- 19. ПОСЛЕДОВАТЕЛЬНЫЕ РЕГИСТРЫ ПОСЛЕДОВАТЕЛЬНЫЕ РЕГИСТРЫ (или РЕГИ-СТРЫ СДВИГА)
- 20. После подачи «n» тактовых импульсов n-битовый последовательный
- 21. В некоторых схемах совмещаются функции параллельного и
- 22. Операцию преобразования параллельного кода в последовательный (сдвиг
- 23. КОЛЬЦЕВЫЕ СЧЕТЧИКИ КОЛЬЦЕВЫЕ СЧЕТЧИКИ - это замкнутые
- 24. Максимальный коэффициент пересчета кольцевых счетчиков равен числу
- 25. tttttС1Q1Q2Q3Q4
- 26. Неприятной особенностью кольцевых счетчиков является возможность сбоев,
- 27. Вопросы для экспресс-контроля1. Чем определяется коэффициент деления
- 28. ЛЕКЦИЯ ОКОНЧЕНАСПАСИБО ЗА ВНИМАНИЕ
- 29. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2ОСНОВНЫЕ ТЕМЫ ЛЕКЦИИ
СУММИРУЮЩИЙ СЧЕТЧИК
ВЫЧИТАЮЩИЙ СЧЕТЧИК
РЕВЕРСИВНЫЙ СЧЕТЧИК
СЧЕТЧИКИ С ПРОИЗВОЛЬНЫМ КОЭФФИ-ЦИЕНТОМ ДЕЛЕНИЯ
ПАРАЛЛЕЛЬНЫЕ
РЕГИСТРЫ
Слайд 3ДВОИЧНЫЕ СЧЕТЧИКИ И СЧЕТЧИКИ НА ИХ ОСНОВЕ
Простейший двоичный счетчик
может быть реализован путем последовательного соединения счетных Т-триггеров
Вход
C1
C
Q1
T1
C
Q2
T2
C
Q3
T3
C
Q4
T4
t
t
t
t
t
С1
Q1
Q2
Q3
Q4
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Слайд 4ВЫЧИТАЮЩИЙ ДВОИЧНЫЙ СЧЕТЧИК
На основе Т-триггеров можно построить ВЫЧИТАЮЩИЙ ДВОИЧНЫЙ
СЧЕТЧИК, если на вход следующего триггера подавать сигналы с инверсного
выхода предыдущего триггераВход
C1
C
Q1
T1
C
Q2
T2
C
Q3
T3
C
Q4
T4
С1
Q1
Q2
Q3
Q4
t
t
t
t
t
15
0
14
13
12
11
10
9
8
7
6
5
4
3
2
1
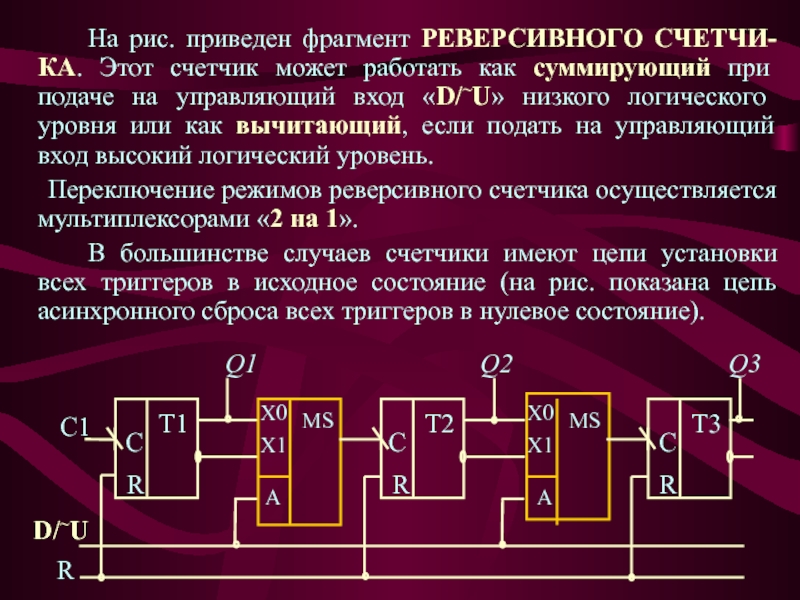
Слайд 5 На рис. приведен фрагмент РЕВЕРСИВНОГО СЧЕТЧИ-КА. Этот счетчик может работать
как суммирующий при подаче на управляющий вход «D/~U» низкого логического
уровня или как вычитающий, если подать на управляющий вход высокий логический уровень.Переключение режимов реверсивного счетчика осуществляется мультиплексорами «2 на 1».
В большинстве случаев счетчики имеют цепи установки всех триггеров в исходное состояние (на рис. показана цепь асинхронного сброса всех триггеров в нулевое состояние).
R
Q1
X0
X1
A
MS
R
C1
C
T1
R
C
T2
Q2
X0
X1
A
MS
R
C
T3
Q3
D/~U
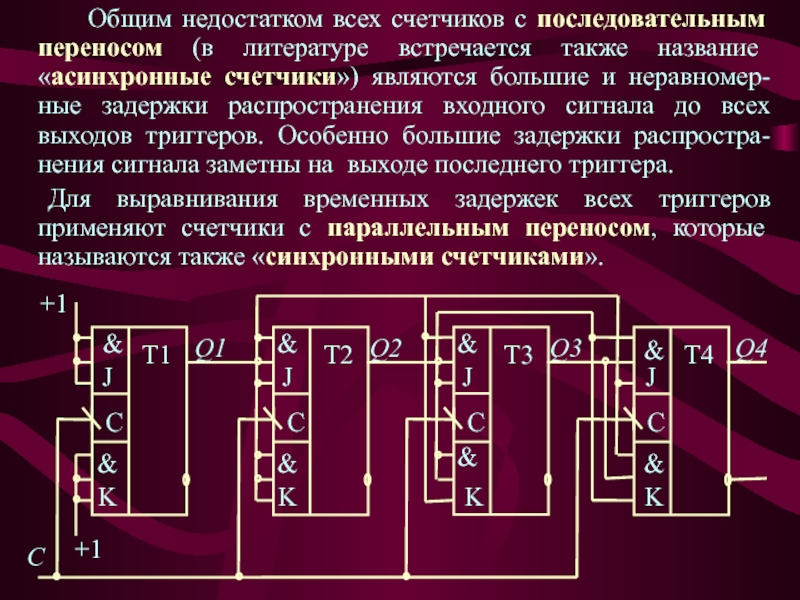
Слайд 6 Общим недостатком всех счетчиков с последовательным переносом (в литературе встречается
также название «асинхронные счетчики») являются большие и неравномер-ные задержки распространения
входного сигнала до всех выходов триггеров. Особенно большие задержки распростра-нения сигнала заметны на выходе последнего триггера.Для выравнивания временных задержек всех триггеров применяют счетчики с параллельным переносом, которые называются также «синхронными счетчиками».
Q3
Q2
C
+1
+1
&
J
&
K
Q1
C
T1
&
J
&
K
C
T2
&
J
&
K
C
T3
Q4
&
J
&
K
C
T4
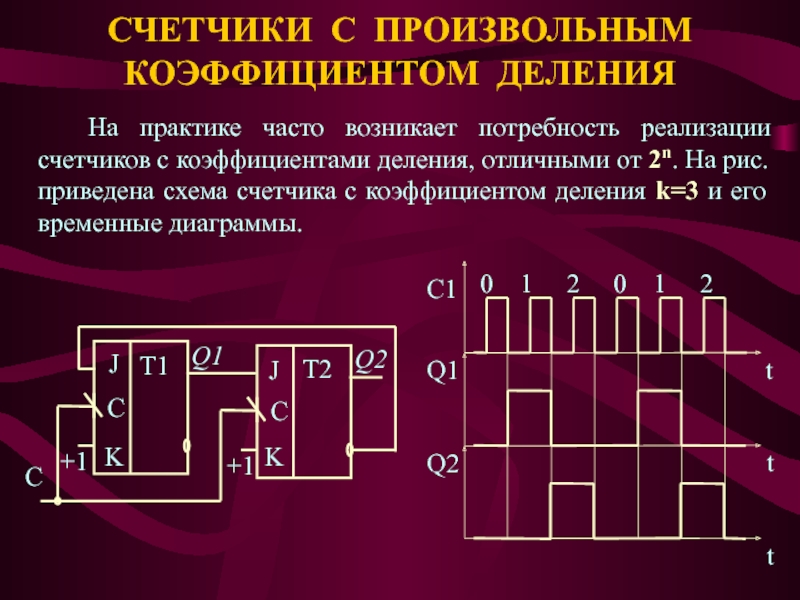
Слайд 7СЧЕТЧИКИ С ПРОИЗВОЛЬНЫМ КОЭФФИЦИЕНТОМ ДЕЛЕНИЯ
На практике часто возникает потребность реализации
счетчиков с коэффициентами деления, отличными от 2n. На рис. приведена
схема счетчика с коэффициентом деления k=3 и его временные диаграммы.+1
J
C
Q1
K
C
T1
+1
J
Q2
K
C
T2
Слайд 9Синтез делителя на k = 14
⮚ определяем количество триггеров
- n:
,
(знак ]...[ - означает ближайшее большее целое),
;
⮚ переводим в
двоичный код число «k-2»;;
⮚ в счетчике с количеством триггеров n выделяем разряды, которым в двоичном коде числа «k–2» соответствуют единицы; с выходов этих триггеров подаем сигналы на элемент Шеффера; выходной сигнал этого элемента является информационным для дополнительного D-триггера; сигнал с выхода D-триггера подается на входы асинхронного сброса всех триггеров счетчика.
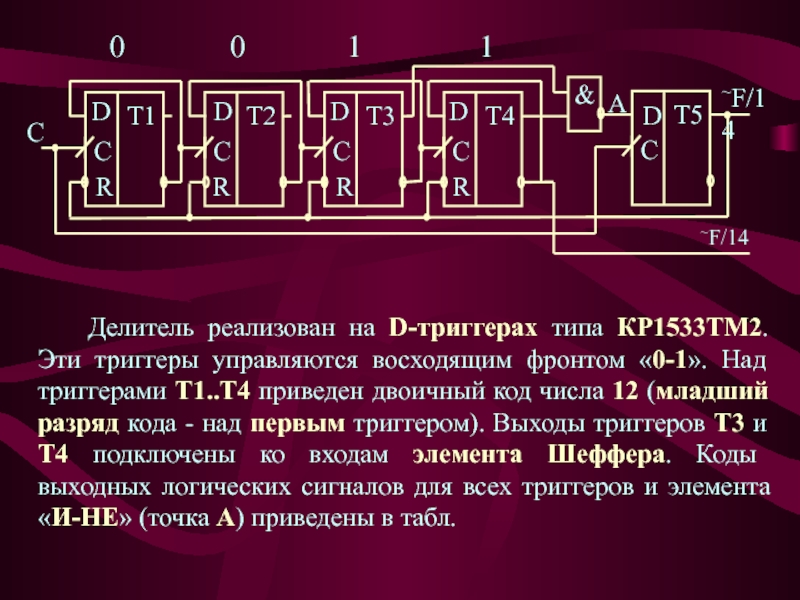
Слайд 10 Делитель реализован на D-триггерах типа КР1533ТМ2. Эти триггеры управляются восходящим
фронтом «0-1». Над триггерами Т1..Т4 приведен двоичный код числа 12
(младший разряд кода - над первым триггером). Выходы триггеров Т3 и Т4 подключены ко входам элемента Шеффера. Коды выходных логических сигналов для всех триггеров и элемента «И-НЕ» (точка А) приведены в табл.A
~F/14
D
C
T1
D
C
T4
D
C
T2
D
C
T3
D
C
T5
0 0 1 1
C
R
R
R
R
~F/14
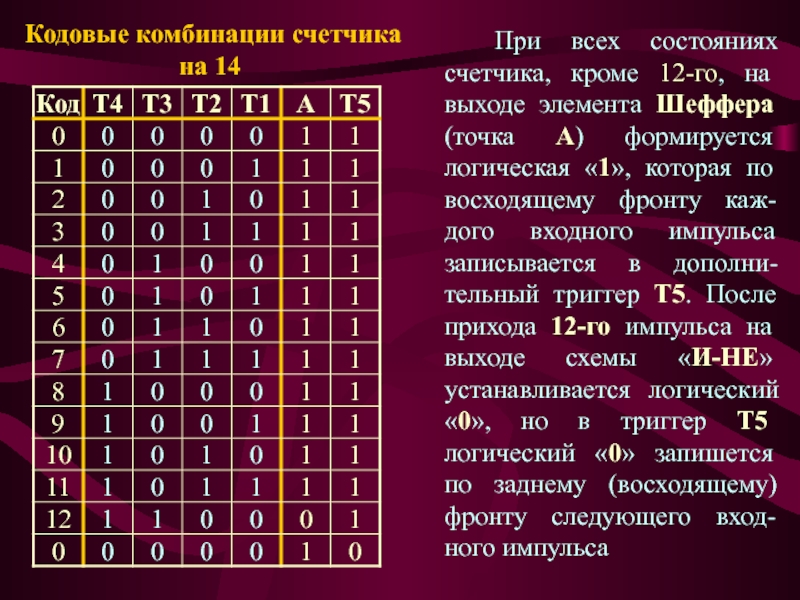
Слайд 11 При всех состояниях счетчика, кроме 12-го, на выходе элемента Шеффера
(точка А) формируется логическая «1», которая по восходящему фронту каж-дого
входного импульса записывается в дополни-тельный триггер Т5. После прихода 12-го импульса на выходе схемы «И-НЕ» устанавливается логический «0», но в триггер Т5 логический «0» запишется по заднему (восходящему) фронту следующего вход-ного импульсаКодовые комбинации счетчика на 14
Слайд 12 После записи в триггер Т5 «нуля» устанавливаются в «0» все
триггеры счетчика (Т1..Т4) по входам асинхронного сброса R. При этом
на выходе элемента Шеффера формируется логическая «1», которая переписывается в триггер Т5 по окончанию следующего входного импульса. Таким образом, счетчик поочередно перебирает все состояния от «0001» до «1100» и имеет два нулевых состояния (см. первую и последнюю строку табл.) Поэтому при реализации счетчика необходимо использовать код: «k-2».Пример №2. Синтезировать четырехразрядный десятичный счетчик (см. вариант 12) на основе J-K-триггеров . Счетчик должен пройти все состояния : 5, 6, 7, 8, 9, A, B, C, D, E – и вернуться в исходное состояние – 5.
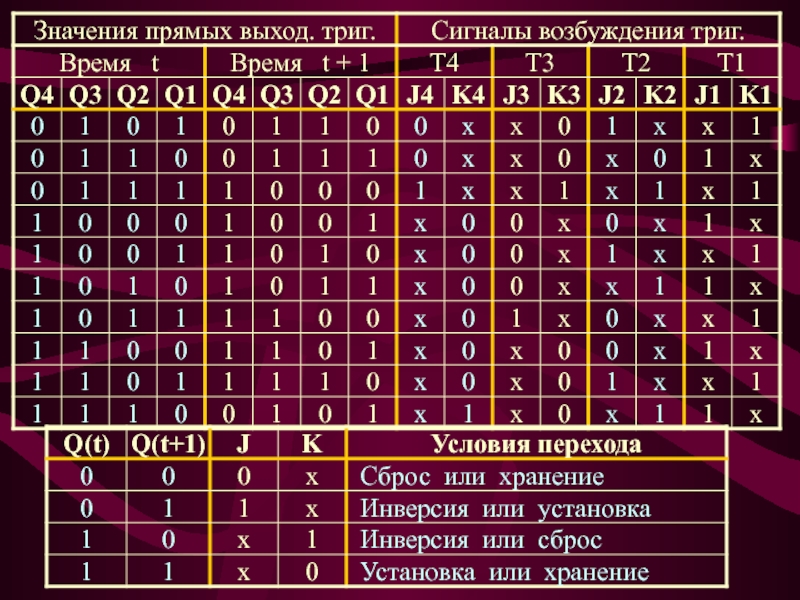
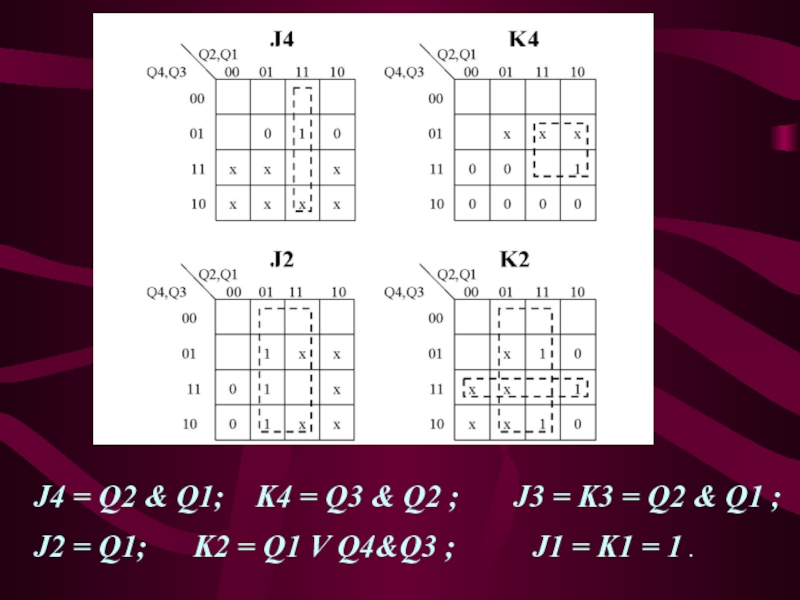
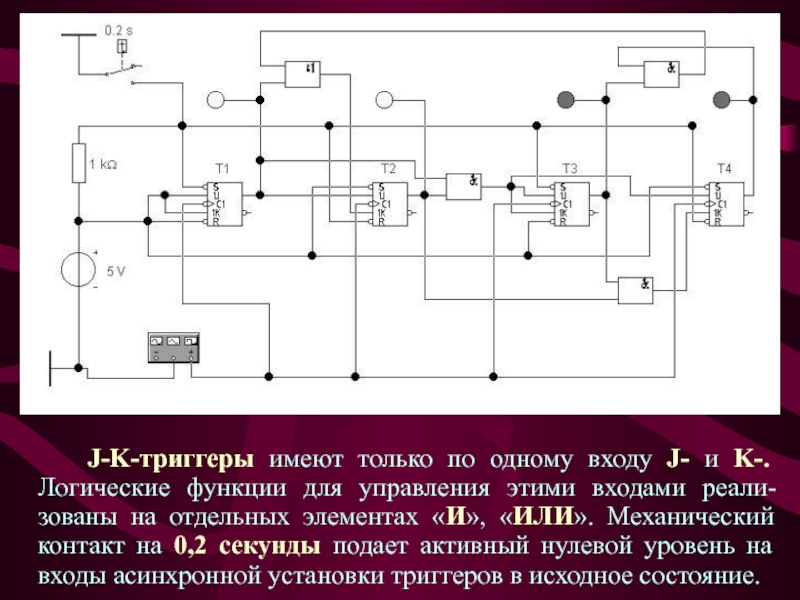
Слайд 15 J-K-триггеры имеют только по одному входу J- и K-. Логические
функции для управления этими входами реали-зованы на отдельных элементах «И»,
«ИЛИ». Механический контакт на 0,2 секунды подает активный нулевой уровень на входы асинхронной установки триггеров в исходное состояние.
Слайд 16ПАРАЛЛЕЛЬНЫЕ И ПОСЛЕДОВАТЕЛЬНЫЕ РЕГИСТРЫ
РЕГИСТРЫ предназначены для выполнения
следу-ющих основных микроопераций над n-разрядным кодом:
⮚ сброс регистра в состояние
«00..0» (все нули);⮚ установка регистра в состояние «11..1» (все единицы);
⮚ прием и хранение в регистре кода числа;
⮚ выдача числа из регистра в прямом или обратном коде;
⮚ сдвиг хранимого в регистре кода на заданное число разрядов вправо или влево;
⮚ преобразование кода из параллельной формы записи в последовательную и наоборот;
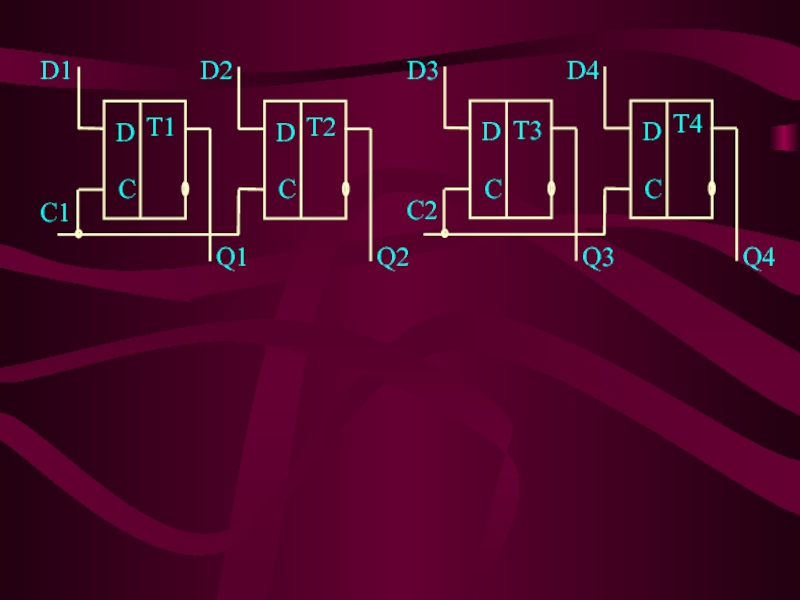
Слайд 17ПАРАЛЛЕЛЬНЫЕ РЕГИСТРЫ
ПАРАЛЛЕЛЬНЫЕ РЕГИСТРЫ применяются для хранения информации, представленной в
виде двоичного кода. Такие регистры должны по тактовому разрешающему сигналу
(это может быть короткий импульс или фронт импульса) принимать параллельный код входной информации и хранить его до прихода следующего разрешающего сигнала.Для построения параллельных регистров наиболее удобны однотактные или двухтактные D-триггеры.
На рис. показан пример параллельного регистра на однотактных D-триггерах, управляемых потенциалом. В момент подачи на синхровходы С1, С2 коротких положительных импульсов двоичный код с входов D1...D4 защелкивается в триггеры и может быть прочитан на выходах Q1...Q4.
Слайд 19ПОСЛЕДОВАТЕЛЬНЫЕ РЕГИСТРЫ
ПОСЛЕДОВАТЕЛЬНЫЕ РЕГИСТРЫ (или РЕГИ-СТРЫ СДВИГА) широко применяются в
цифровой вычислительной технике для преобразования последователь-ного кода в параллельный, или
параллельного в последовательный.Последовательные регистры можно реализовать ТОЛЬКО на двухтактных триггерах, управляемых ФРОНТОМ. На рис. приведена схема сдвигающего регистра на последовательно соединенных D-триггерах.
Qn
Q2
Q3
Q1
D1
C
T1
C
D
T2
C
D
…
T3
C
D
Tn
C
D
…
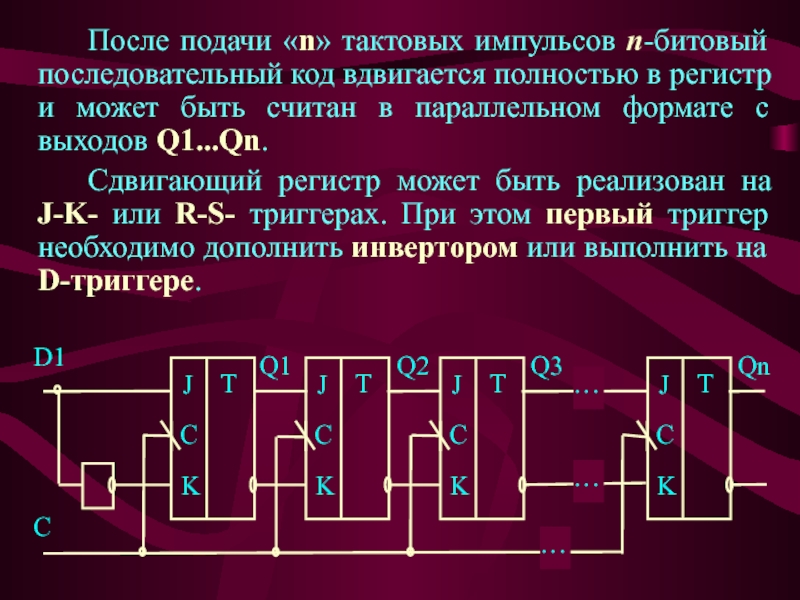
Слайд 20 После подачи «n» тактовых импульсов n-битовый последовательный код вдвигается полностью
в регистр и может быть считан в параллельном формате с
выходов Q1...Qn.Сдвигающий регистр может быть реализован на J-K- или R-S- триггерах. При этом первый триггер необходимо дополнить инвертором или выполнить на D-триггере.
T
J
Q1
K
C
T
J
Q2
K
C
T
J
Q3
K
C
T
J
Qn
K
C
D1
C
…
…
…
Слайд 21 В некоторых схемах совмещаются функции параллельного и последовательного регистров. На
рис. приведена схема УНИВЕРСАЛЬНОГО РЕГИСТРА на двухтактных D-триггерах, управляемых фронтом,
и мультиплексорах «2 на 1».На входы D1..Dn подается параллельный код для записи в регистр по фронту «0-1» входного синхроимпульса при низком логическом уровне на управляющем входе S/~P.
После подачи высокого логического уровня на управляю-щий вход S/~P регистр переводится в режим последовательного сдвига. На вход Ds подается последовательный код для преобразования его в параллельный. Преобразованный парал-лельный код может быть прочитан с выходов Q1..Qn.
Qn
T1
C
D
А
Q1
C
D1
Ds
MS
X1
X0
А
MS
X1
X0
D2
Tn
C
D
А
MS
X1
X0
…
Q2
Dn
…..
…..
T2
C
D
S/~P
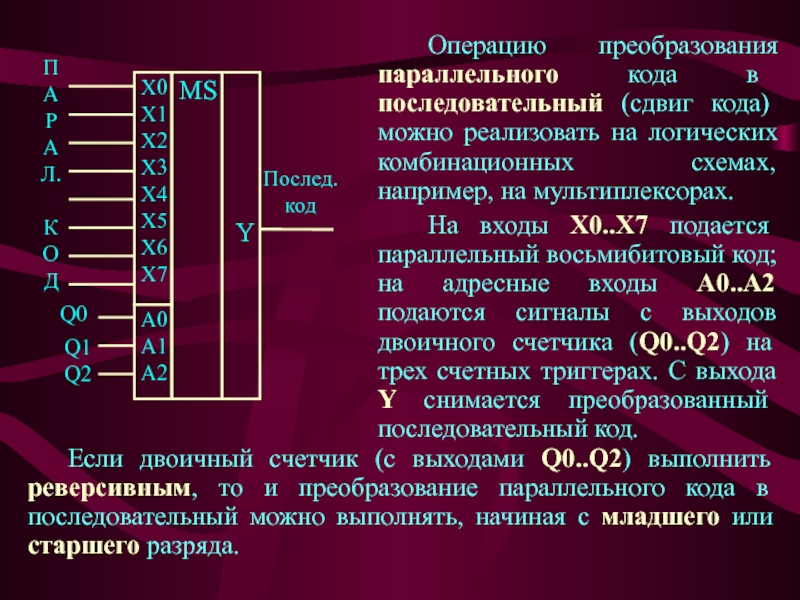
Слайд 22 Операцию преобразования параллельного кода в последовательный (сдвиг кода) можно реализовать
на логических комбинационных схемах, например, на мультиплексорах.
На входы X0..X7 подается
параллельный восьмибитовый код; на адресные входы А0..А2 подаются сигналы с выходов двоичного счетчика (Q0..Q2) на трех счетных триггерах. С выхода Y снимается преобразованный последовательный код. Если двоичный счетчик (с выходами Q0..Q2) выполнить реверсивным, то и преобразование параллельного кода в последовательный можно выполнять, начиная с младшего или старшего разряда.
ПАРАЛ.
КОД
X0
X1
X2
X3
X4
X5
X6
X7
A0
A1
A2
MS
Y
Q0
Q1
Q2
Послед. код
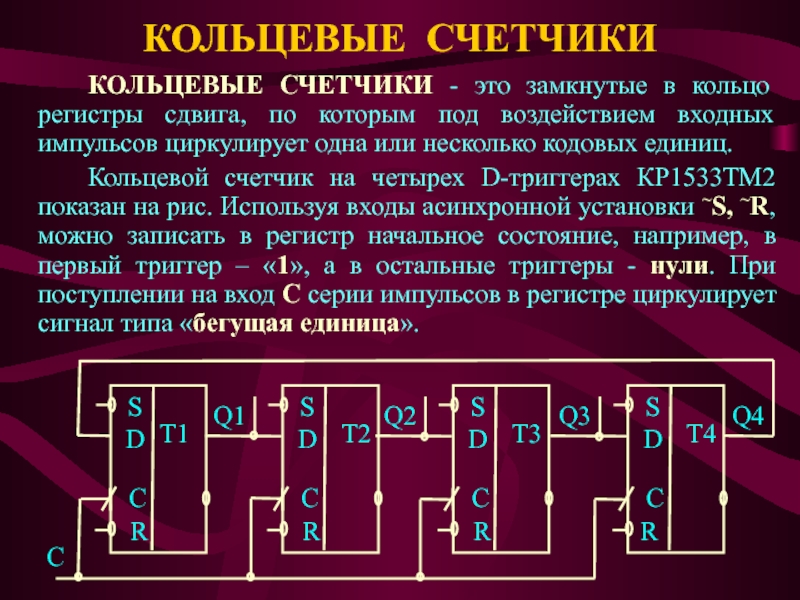
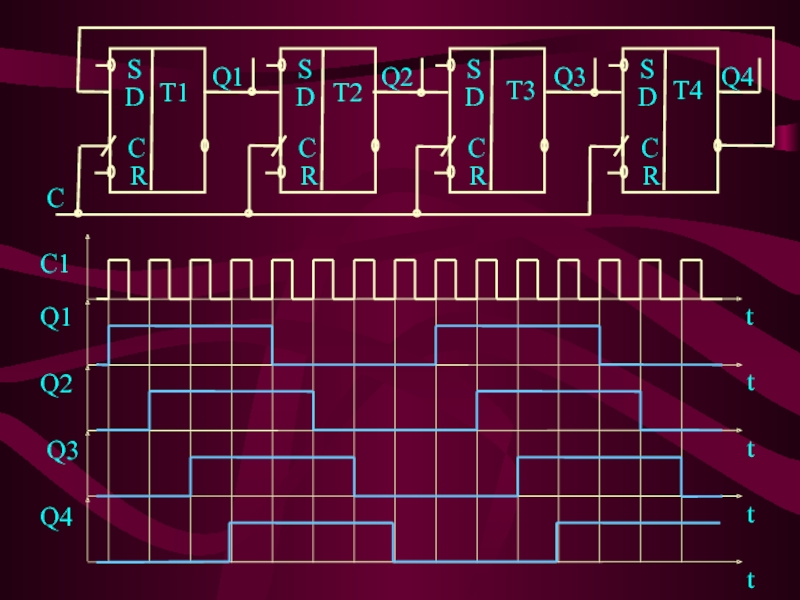
Слайд 23КОЛЬЦЕВЫЕ СЧЕТЧИКИ
КОЛЬЦЕВЫЕ СЧЕТЧИКИ - это замкнутые в кольцо регистры
сдвига, по которым под воздействием входных импульсов циркулирует одна или
несколько кодовых единиц.Кольцевой счетчик на четырех D-триггерах КР1533ТМ2 показан на рис. Используя входы асинхронной установки ~S, ~R, можно записать в регистр начальное состояние, например, в первый триггер – «1», а в остальные триггеры - нули. При поступлении на вход С серии импульсов в регистре циркулирует сигнал типа «бегущая единица».
Q2
Q1
C
R
T1
C
D
S
R
T2
C
D
S
R
T3
C
D
S
Q3
R
T4
C
D
S
Q4
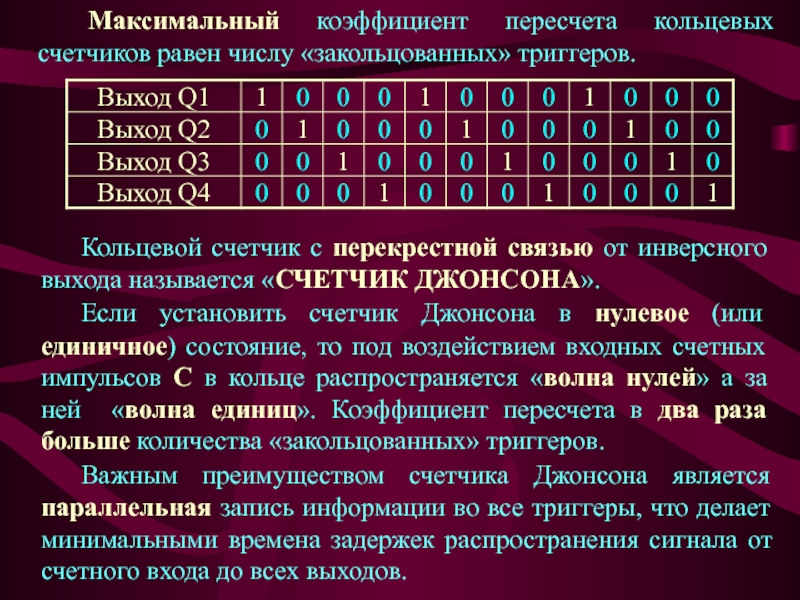
Слайд 24 Максимальный коэффициент пересчета кольцевых счетчиков равен числу «закольцованных» триггеров.
Кольцевой счетчик
с перекрестной связью от инверсного выхода называется «СЧЕТЧИК ДЖОНСОНА».
Если установить
счетчик Джонсона в нулевое (или единичное) состояние, то под воздействием входных счетных импульсов С в кольце распространяется «волна нулей» а за ней «волна единиц». Коэффициент пересчета в два раза больше количества «закольцованных» триггеров.Важным преимуществом счетчика Джонсона является параллельная запись информации во все триггеры, что делает минимальными времена задержек распространения сигнала от счетного входа до всех выходов.
Слайд 26 Неприятной особенностью кольцевых счетчиков является возможность сбоев, вызванных появлением лишних
или исчезновением нужных кодовых единиц в кольце. Причем эти сбои,
раз возникнув, могут существовать во время счета неопределенно долго, если не принять специальных мер по их устранению.Слайд 27Вопросы для экспресс-контроля
1. Чем определяется коэффициент деления счетчиков?
2. Чем отличаются
суммирующие счетчики от вычи-тающих?
3. Методы реализации реверсивных счетчиков.
4. Назовите преимущества и недостатки
счетчиков с последовательным и параллельным переносом.5. На каких триггерах можно реализовать счетчики?
6. Назовите назначение параллельных и последо-вательных регистров.
7. На каких триггерах можно реализовать параллель-ные и последовательные регистры?
8. Как можно реализовать кольцевые счетчики?




![РЕГИСТРЫ и КОЛЬЦЕВЫЕ СЧЕТЧИКИ ДВОИЧНЫЕ СЧЕТЧИКИ и СЧЕТЧИКИ НА ИХ ОСНОВЕ Синтез делителя на k = 14 ⮚ определяем количество триггеров - Синтез делителя на k = 14 ⮚ определяем количество триггеров - n: , (знак ]...[ - означает ближайшее большее](/img/thumbs/73f4f5bcf74f77bb58ecfb44f138ac39-800x.jpg)