Слайд 1Российский государственный университет им. И. Канта
Факультет информатики и прикладной
математики
Кафедра компьютерного моделирования и информационных систем
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ
Александр Васильевич Колесников
доктор
технических наук, профессор
Калининград, 2010
Слайд 2Понятие информатики
Информатика - научная дисциплина, изучающая вопросы поиска, сбора, хранения,
преобразования и использования информации в различных сферах человеческой деятельности.
Слайд 3Структура современной информатики
Рассмотрим составные части «ядра» информатики - относительно
самостоятельные научные дисциплины.
Теоретическая информатика - часть информатики, включающая математические
разделы: теория алгоритмов и автоматов, теория информации и теория кодирования, теория формальных языков и грамматик, исследование операций, искусственный интеллект. Эта часть информатики использует математические методы для изучения процессов обработки информации.
Вычислительная техника - раздел, в котором разрабатываются общие принципы построения архитектур вычислительных систем. Примеры классических решений – фон-Неймановская архитектура компьютеров первых поколений, шинная архитектура ЭВМ старших поколений, архитектура параллельной (многопроцессорной) обработки информации.
Слайд 4Структура современной информатики
Программирование - деятельность, связанная с разработкой системного
(алгоритмические языки и компиляторы, интерфейсы, ОС) и прикладного (редакторы текстов,
машинная графика, СУБД) программного обеспечения.
Информационные системы - раздел информатики, связанный с анализом потоков информации в сложных системах, их оптимизацией, структурированием, принципами хранения и поиска информации.
Искусственный интеллект - область информатики, изучающая вычисления, позволяющие чувствовать, рассуждать и действовать. Основные направления разработок - моделирование рассуждений, компьютерная лингвистика, машинный перевод, создание экспертных систем, распознавание образов и другие.
Слайд 5Определение понятия «информация»
Слово «информация» (от лат. «сообщение», «разъяснение») - основополагающий
термин информатики. Впервые введен в книге Н.Винера «Кибернетика». В узком
смысле - "количество информации".
Информация - это содержание сообщения, сигнала, памяти, а также сведения, содержащиеся в сообщении, сигнале или памяти.
Информация - сведения об объектах и явлениях окружающей среды, их параметрах, свойствах и состоянии, которые уменьшают имеющуюся о них степень неопределённости , неполноты знаний.
Слайд 6Понятие информации
В 1948 году К.Шеннон, закладывая основы теории связи предложил
определять информацию с точки зрения обмена данными между источником и
приемником.
Клод Элвуд Шеннон, американский математик, инженер, доктор наук, профессор, основатель теории информации
Данные (от лат. data) — представление фактов и идей в формализованном виде, пригодном для передачи и обработки в некотором информационном процессе.
Слайд 7Понятие информации
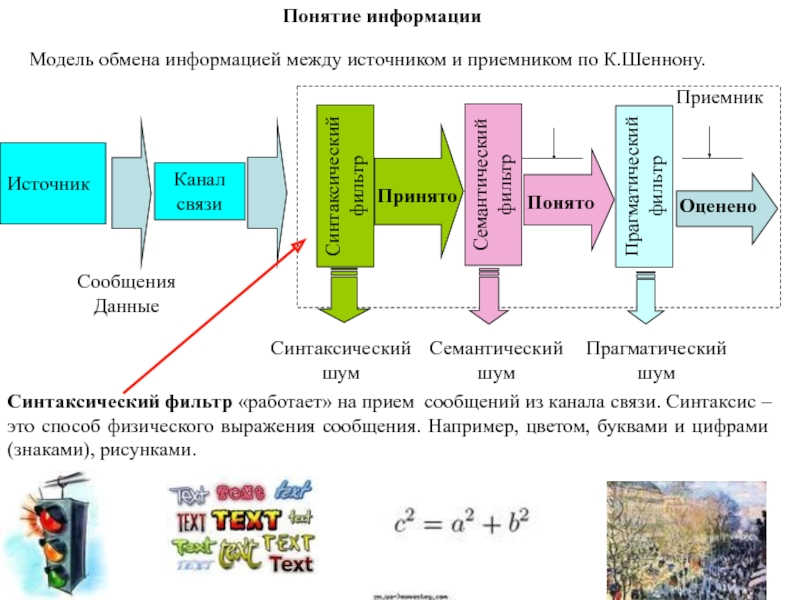
Модель обмена информацией между источником и приемником по К.Шеннону.
Синтаксический
фильтр «работает» на прием сообщений из канала связи. Синтаксис –
это способ физического выражения сообщения. Например, цветом, буквами и цифрами (знаками), рисунками.
Слайд 8Понятие информации
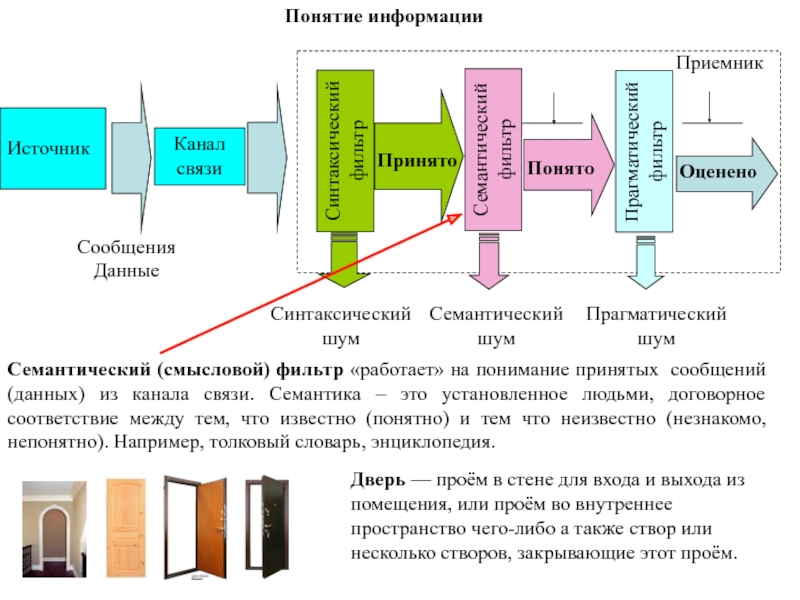
Семантический (смысловой) фильтр «работает» на понимание принятых сообщений (данных)
из канала связи. Семантика – это установленное людьми, договорное соответствие
между тем, что известно (понятно) и тем что неизвестно (незнакомо, непонятно). Например, толковый словарь, энциклопедия.
Дверь — проём в стене для входа и выхода из помещения, или проём во внутреннее пространство чего-либо а также створ или несколько створов, закрывающие этот проём.
Слайд 9Понятие информации
Прагматический (смысловой) фильтр - устанавливает ценность принятых и понятых
данных. Прагматика – значимость, ценность данных для чего либо. Например,
если Вы видите и понимаете сигналы светофора, но не пересекаете перекресток, то данные от светофора для Вас не имеют значения.
Источник
Канал связи
Синтаксический фильтр
Семантический фильтр
Прагматический фильтр
Приемник
Принято
Понято
Оценено
Синтаксический шум
Семантический шум
Прагматический шум
Сообщения Данные
Слайд 10Понятие информации
Информация – данные, которые приняты (синтаксис), поняты (семантика) и
оценены как полезные (прагматика).
Слайд 11Пирамида знаний
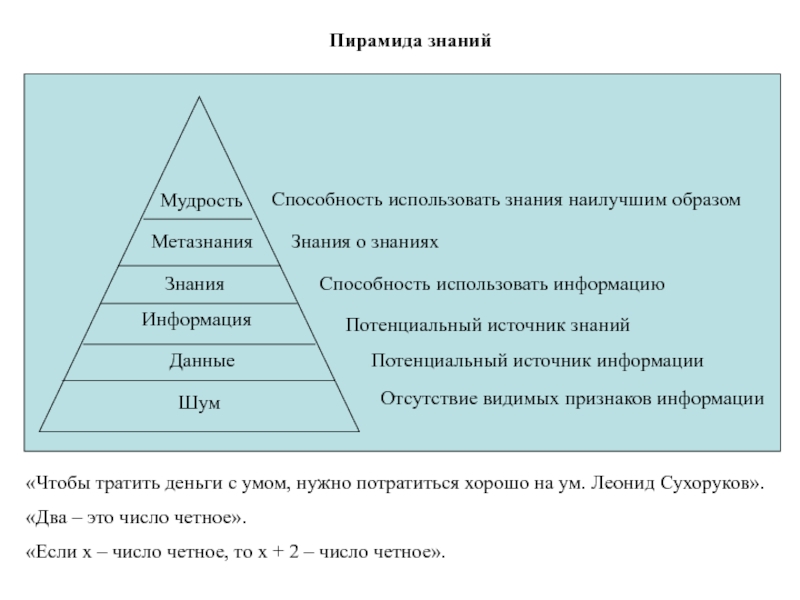
Отсутствие видимых признаков информации
Шум
Данные
Информация
Знания
Метазнания
Мудрость
Потенциальный источник информации
Потенциальный источник знаний
Способность использовать
информацию
Знания о знаниях
Способность использовать знания наилучшим образом
«Чтобы тратить деньги с
умом, нужно потратиться хорошо на ум. Леонид Сухоруков».
«Два – это число четное».
«Если x – число четное, то x + 2 – число четное».
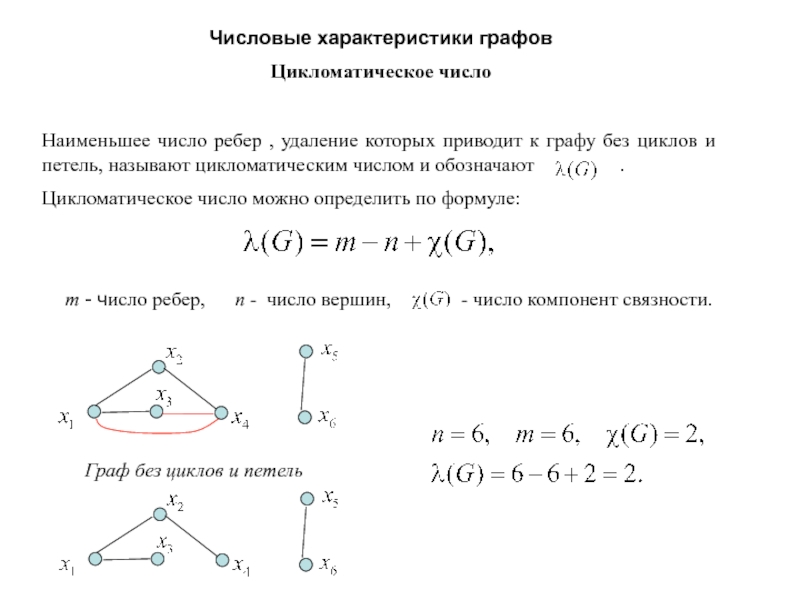
Слайд 12Количество информации - числовая величина, адекватно характеризующая актуализируемую информацию по
разнообразию, сложности, структурированности (упорядоченности), определенности, выбору состояний отображаемой системы.
Меры информации
Мера
количества информации – то с помощью чего измеряют информацию.
Точная наука невозможна без измерений. Для измерений необходимы опорные метки — меры. Чтобы стать общепринятыми, они должны быть простыми, понятными и общедоступными.
Слайд 13Меры информации
Пример. Определить количество информации в сообщении на русском языке
содержащем ФИО, год, месяц, дату рождения: Иван Петрович Семенов 1983
11 03.
Число букв и пробелов – 30. Число цифр – 8.
В сообщениях на русском языке – 33 буквы плюс пробел. Десятичных цифр – 10. Тогда:
Ральф Хартли, американский ученый, пионер теории информации
Слайд 14Меры информации
Мера Хартли
Формула Хартли отвлечена от семантических и качественных свойств
информации. Это положительная сторона формулы. Но имеется и минус: формула
не учитывает вероятность появления символа в сообщении.
Вероя́тность — численная мера возможности наступления события. На практике вероятность события — это отношение количества тех наблюдений, при которых рассматриваемое событие наступило, к общему количеству наблюдений. Такая трактовка допустима при достаточно большого количества наблюдений.
Слайд 15Меры информации
Мера К. Шеннона. Мера К. Шеннона учитывает вероятность появления
символа в сообщении.
Повседневный опыт подсказывает, что часто происходящие события, дают
нам мало информации. Возьмем, сообщение «студенты внимательны на лекции». Это привычное известие не привлекло бы к себе никакого внимания, в то время, как сообщение «студент доказал теорему» университетская газеты напечатала бы крупным шрифтом.
Мало информации
Много информации
Вывод: частые, ожидаемые события несут мало информации и, наоборот, редкие, т.е. неожиданные события, обладают высоким информационным содержанием.
Следовательно, информация (I) и вероятность (p) находятся в обратно пропорциональной зависимости.
Мера К.Шеннона
Слайд 18Ситуация 1
Ситуация 2
Меры информации
Слайд 19Знак минус не означает, что количество информации в сообщении –
отрицательная величина. Объясняется это тем, что вероятность р, согласно определению, меньше
единицы, но больше нуля. Так как логарифм числа, меньшего единицы, т.е. – величина отрицательная, то произведение вероятности на логарифм числа будет положительным.
где , - число сигналов i – го типа
Меры информации
Слайд 20Чтобы определить среднее количество информации, приходящееся на один сигнал, т.е.
удельную информативность источника, нужно это число разделить на N. При
неограниченном росте приблизительное равенство перейдет в точное. В результате будет получено асимптотическое соотношение – формула Шеннона:
Формула, предложенная Хартли, представляет собой частный случай более общей формулы Шеннона. Если в формуле Шеннона принять, что
, то:
Мера Шеннона
Меры информации
Слайд 21Пример. Определить количество информации в сообщении на русском языке содержащем
ФИО, год, месяц, дату плюс пробел. Десятичных цифр – 10.
Тогда: рождения: Иван Петрович Семенов 1983 11 03. Число букв и пробелов – 30. Число цифр – 8. В сообщениях на русском языке – 33 буквы .
Мера Шеннона
Таблица вероятностей появления букв русского алфавита в сообщениях
Меры информации
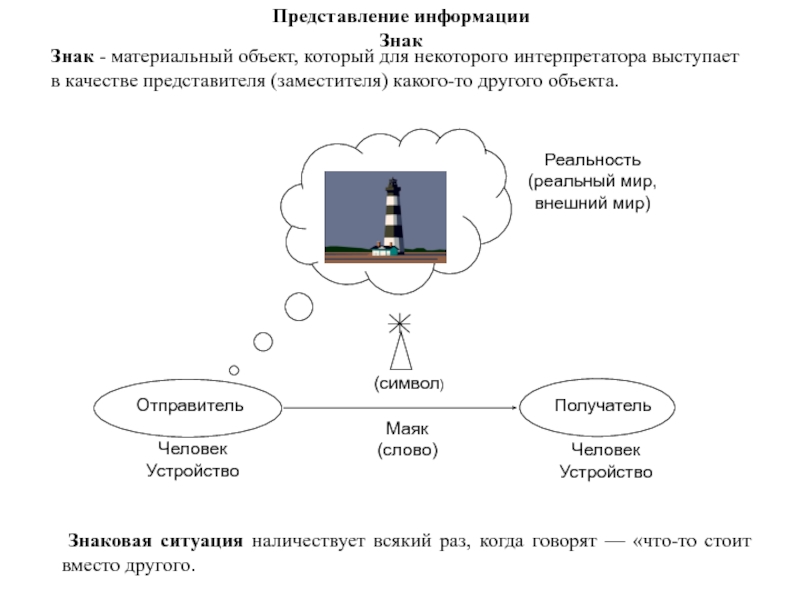
Слайд 22Представление информации Знак
Отправитель
Получатель
Человек
Устройство
Человек
Устройство
(символ)
Маяк
(слово)
Реальность
(реальный мир,
внешний мир)
Знак - материальный объект, который для некоторого интерпретатора выступает
в качестве представителя (заместителя) какого-то другого объекта.
Знаковая ситуация
наличествует всякий раз, когда говорят — «что-то стоит вместо другого.
Слайд 23Знаковая система — совокупность условных знаков и правил их взаимосвязи.
Это мощный инструмент решения задач. Чтобы задать знаковую систему необходимо:
1) определить набор базисных знаков, придавая каждому из них какое-то определенное значение; 2) сформулировать правила, определяющие какие производные знаки, построенные из нашего набора знаков корректные, а какие — нет. Набор таких правил - это грамматика знаковой системы.
Высказывание в терминах знаковой системы, может содержать определенный смысл. Если субъекту известны правила прочтения знаков этой системы, то эти записи могут быть восприняты им, и могут сформировать соответствующую мысль.
Язык. Система счисления. Музыка. Религия. Мода .
Знаковая система
Примеры знаковых систем
Слайд 24
Основателем семиотики - американский логик, философ и естествоиспытатель Чарльз Пирс, который
и предложил её название.
Представление информации Семиотика
Чарльз Пирс,
американский философ, логик,
математик, основатель семиотики
Системы средств, используемые человеком для обмена информацией - знаковые или семиотическими, т. е. системами знаков и правил их потребления. Наука, изучающая знаковые системы называется СЕМИОТИКОЙ или семиологией ( от греч. слова sema — знак).
Современная фрактальная семиотика
Слайд 25Модель знака (треугольник)
Г. Фреге
Знак по Фреге – это
объект, обладающий синтаксисом, семантикой и прагматикой
Треугольник Фреге – основа современной
семиотики.
Готлоб Фреге,
немецкий логик, философ и математик
Слайд 26Модель знаковой системы
Будем называть знаковой системой четверку следующего вида:
где F
– множество знаков; U - универсуум, т.е. множество денотатов; Z
– система знаний, т.е. множество понятий, в которых описываются концепты и их взаимоотношения; I – интерпретации, относящие знаку его денотат или концепт.
Модель знаковой системы
Слайд 27
Основная и всеобъемлющая знаковая система, обеспечивающая развитие интеллекта человека и
процессы познания - это естественный язык.
Естественный язык — это любой
язык, практикуемый в общении людей. Естественными языками являются все разговорные языки — например: русский, английский, или китайский.
2) Естественный язык - это система, которая осуществляет функции знаковой поддержки различных интеллектуальных операций, в том числе базовых операций обобщения и абстракции.
Естественный язык как знаковая система
Слайд 28Главные особенности естественного языка
Первая проблема – коммуникация людей (устройств) с
различными моделями внешнего мира.
«Зло – это плохо»
«Списывать на экзамене
– это хорошо»
«Зло – это хорошо»
«Списывать на экзамене – это плохо»
Слайд 29Особенности естественного языка
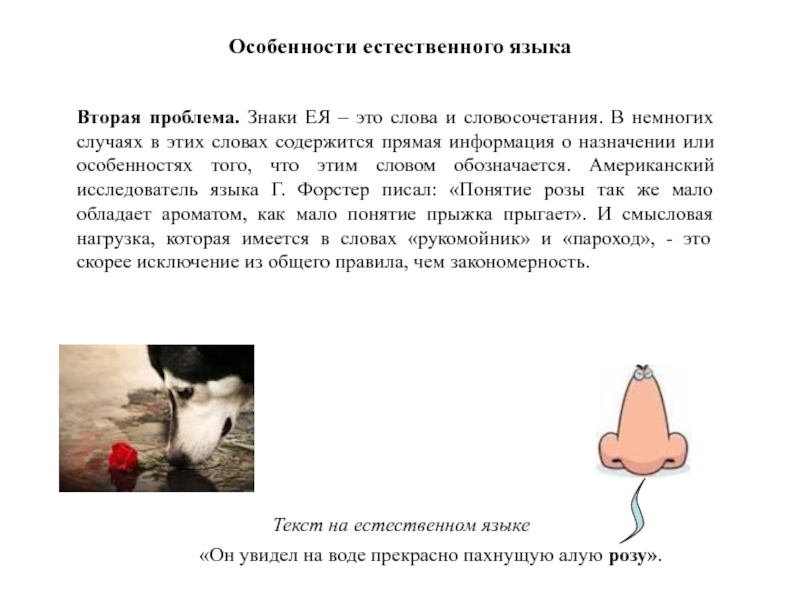
Вторая проблема. Знаки ЕЯ – это слова и
словосочетания. В немногих случаях в этих словах содержится прямая информация
о назначении или особенностях того, что этим словом обозначается. Американский исследователь языка Г. Форстер писал: «Понятие розы так же мало обладает ароматом, как мало понятие прыжка прыгает». И смысловая нагрузка, которая имеется в словах «рукомойник» и «пароход», - это скорее исключение из общего правила, чем закономерность.
«Он увидел на воде прекрасно пахнущую алую розу».
Текст на естественном языке
Слайд 30Ананас — хороший.
Апельсин — хороший, маленький, светлый.
Арбуз
— большой, гладкий.
Астра — яркий.
Баобаб
— большой, величественный, могучий.
Береза — светлый, яркий.
Василек — светлый.
Гвоздика — яркий.
Дуб — большой, сильный, красивый, могучий.
Дубрава — большой, красивый, величественный.
Ель — красивый.
Хиляк — плохой, слабый, хилый, медлительный.
Хлюпик — слабый, медлительный.
Хрыч — плохой, грубый, отталкивающий, злой.
Цаца — плохой.
Чистюля — хороший, светлый.
Звуковая форма слова женщина получила компьютерные оценки, явно противоречащие признаковому значению: «темный», «отталкивающий», «тяжелый», «устрашающий», «низменный», «злой».
Звук. Текст. Смысл.
Из работ профессора А.П. Журавлева
Слайд 31Искусственные языки
Языки программирования и компьютерные языки — языки для автоматической
обработки информации с помощью ЭВМ. Например, язык программирования Паскаль и
язык моделирования GPSS.
Информационные языки— языки, используемые в различных системах обработки информации. Например, язык команд и иконок операционной системы.
Формализованные языки науки — языки, предназначенные для символической записи фактов и теорий математики, логики, химии и других наук. Например, язык исчисления высказываний в математической логики, язык теории множеств и отношений дискретной математики.
Слайд 32Формализованный язык
Формализованный язык - в широком смысле – любая совокупность
некоторым образом специализированных языковых средств с (более или менее) точно
фиксированными правилами образования «выражений» (синтаксис.) и приписывания этим выражениям определённого смысла (семантика).
Использование формализованного языка – характерная особенность математической логики, которую часто и определяют как «предмет формальной логики, изучаемый посредством построения формализованных языков».
В отличие от естественных языков формальным языкам присущи четко сформулированные правила семантической интерпретации и синтаксического преобразования используемых знаков, а также то, что смысл и значение знаков не изменяется в зависимости от каких-либо прагматических обстоятельств (например, от контекста).
Слайд 33Основные объекты теории формальных языков
Основные объекты теории формальных языков –
цепочки символов.
Алфавит (иногда говорят – словарь) – непустое множество
, элементы которого – это символы (слова) –
Цепочки символов над алфавитом - это конечные упорядоченные последовательности символов.
Пример. Пусть имеем алфавит .
Тогда существуют цепочки: e, a, b, c, ab, ba,…, aaabb, bbbbaacc,… .
Слайд 34Пустая цепочка обозначается e. Длина цепочки – это число содержащихся
в ней символов:
= 8.
Множество всех возможных цепочек над алфавитом обозначается .
Для цепочек символов естественным образом определена операция конкатенации (склеивания): .
По определению .
Иногда вместо пишут .
Язык над словарем - некоторое множество цепочек символов, то есть подмножество множества .
Основные объекты теории формальных языков
Слайд 35Способы описания формальных языков
Словесное описание – перечисление всех свойств цепочек
символов, принадлежащих данному языку.
Алгебраическое описание – указание, как с помощью
алгебраических правил конструируются цепочки данного языка.
Порождающие правила – набор инструкций, по которым, исходя из некоторого начального множества символов (может быть и одного), строятся все цепочки языка. Такой способ часто используется при описании языков программирования.
Алгоритм распознавания – последовательность действий, с помощью которой может быть проведен анализ цепочки символов и установлено – принадлежит эта цепочку языку или нет. Удобно рассматривать в некоторое устройства - распознающий автомат, который переходит из состояния в состояние, в зависимости от того, какой символ поступает на его вход.
Слайд 36Примеры описания формальных языков
1) Пусть
. Все цепочки из
трех символов этого алфавита легко выписать.
2) Цепочки из нулей и единиц, начинающиеся с единицы.
3) ; - простой пример алгебраического описания языка.
4) Множество цепочек языка L над алфавитом , в которых для каждой левой скобки есть парная ей правая скобка.
Слайд 37Применение формальных языков
Формальные языки широко применяются в науке и технике.
Формальный язык - средство более точного представления знаний, чем естественный
язык, а следовательно, средством более точного и объективного обмена информацией между людьми.
Формальные языки часто конструируются на базе языка математики. С точки зрения информатики, среди формальных языков наиболее значительную роль играют язык алгебры логики и языки программирования.
Возникновение языков программирования приходится на начало 50-х годов XX века.
Языков программирования и их разновидностей насчитывается несколько тысяч.
Слайд 38Формальная грамматика
Грамматика языка – это набор средств для его
описания. Различают порождающие и распознающие грамматики, в зависимости от того,
какая задача ставится: строить новые цепочки языка или определять принадлежит или нет некоторая цепочка языку.
Формальной порождающей грамматикой G называется следующая совокупность четырех объектов:
где - терминальный алфавит (словарь); буквы этого алфавита называются терминальными символами; из них строятся цепочки порождаемые грамматикой;
- нетерминальный, вспомогательный алфавит (словарь); буквы этого алфавита используются при построении цепочек; они могут входить в промежуточные цепочки, но не должны входить в результат порождения; f - начальный символ грамматики ; P - множество правил вывода или порождающих правил вида
, где a и b - цепочки, построенные из букв алфавита и , который называют полным алфавитом (словарем) грамматики G.
Слайд 39Язык порождаемый грамматикой
В множество правил грамматики могут также входить правила
с пустой правой частью вида .
Чтобы избежать неопределенности из-за отсутствия символа в правой части правила, условимся использовать символ пустой цепочки, записывая такое правило в виде e.
Из терминальных символов состоят цепочки языка, порожденного грамматикой. Аксиомой называется символ в левой части первого правила вывода грамматики.
Пусть - правило грамматики G и - цепочка символов. Тогда цепочка может быть получена из цепочки a путем применения правила p (т.е. заменой в a цепочки t на g). В этом случае говорят, что цепочка b непосредственно выведена из цепочки a и обозначают a b .
Если задано множество цепочек , таких что существует последовательность непосредственных выводов:
то такую последовательность называют выводом из в грамматике G и
обозначают . Отношение отличается от отношения и является его транзитивным замыканием.
Множество конечных цепочек терминального алфавита грамматики G, выводимых из начального символа f, называется языком, порождаемым грамматикой G и обозначается L( G):
L( G) = {v | } .

Слайд 40Язык, порождаемый грамматикой
Пример.
Дана грамматика
в
которой = {а, b}, = {S}, f = S, Р = {S →aSb, S → ab}. Определить язык, порождаемый этой грамматикой.
Решение. Выведем несколько цепочек языка, порождаемого данной грамматикой:
S → ab;
S → aSb => aabb;
S → aSb =>aaSbb => aaabbb; . . .
Определим язык, порожденный данной грамматикой алгебраическим способом:
L(G) = { | n > 0}.
Поскольку каждый язык является множеством, можно рассматривать операции объединения, пересечения и разности языков, заданных над одними тем же алфавитом (обозначения ∪ , ∩ , \ ). Язык L над алфавитом Σ представляет собой множество цепочек над Σ. Необходимо различать пустой язык L = и язык, содержащий только пустую цепочку: L = {e} ≠ .
Слайд 42Формальные системы
Формальной системой будем называть следующую четверку (конструктивное определение):
где
D - алфавит, как рекурсивно перечислимый набор произвольных
символов; C – синтаксис, как рекурсивно перечислимое непустое множество правил построения формул (слов) из символов алфавита; A - аксиоматика конечное непустое множество формул (слов), называемых аксиомами; P- множество продукционных правил (должно быть рекурсивно перечислимым и не пустым).
Слайд 43Примеры составляющих формальной системы
Примеры алфавита
{а,б,в,г,д,…,э,ю,я}, {,,,,}, {1,2,3,4,5,6,7,8,9,0,(,),+,-,*,/}, Код ANSI
Пример синтаксиса
Используется
алфавит {1,2,3,4,5,6,7,8,9,0,(,),+,-,*,/}
‹Цифра› ::= 1|2|3|4|5|6|7|8|9|0
‹ПоложительноеЧисло› ::= ‹Цифра›|‹Цифра›‹ПоложительноеЧисло›
‹ОтрицательноеЧисло› ::= - ‹ПоложительноеЧисло›
‹Число› ::=
‹ПоложительноеЧисло›| ‹ОтрицательноеЧисло›
‹Оператор› ::= +|-|*|/
‹Выражение› ::= ‹Число›|(‹Выражение›)| ‹Выражение›‹Оператор›‹Выражение›
Примеры аксиом
‹Число›*1 = ‹Число›
‹Число›*0 = 0
‹Число›+0 = ‹Число›
Такими аксиомами можно дополнить теорию чисел (формальную арифметику)
‹Число›/0 = ‹Число›
Может ли теория чисел содержать такую аксиому?
Примеры продукционных правил
A→ B, (В → C) (A → C)
x ·z+y ·z (x+y)·z
Слайд 44Примеры формальных систем
Пример 1.
Алфавит: {а, b, #}
Синтаксис формул:
‹Формула› ::= а|b|#
‹Формула› ::= ‹Формула›‹Формула›
Аксиома: а#а
Продукционные правила: x#y
bx#yb
Некоторые теоремы: а#а, ba#аb, bba#аbb, bbba#аbbb, …
Слайд 45Примеры формальных систем
Пример 2: исчисление высказываний
Алфавит
A1 = {p, q, …,
z, pp, рq, … zz, ppp, …}
A2 = { ,
, (, )}
Синтаксис формул
‹Формула› ::= a | aA1
‹Формула› ::= (‹Формула›)
‹Формула› ::= ‹Формула›
‹Формула› ::= ‹Формула› ‹Формула›
Аксиомы
Продукционное правило (правило заключения)
Теоремы : (правило силлогизма)
(правило перестановки)
Слайд 46Формальные теории
Теоремой в теории формальных систем называется аксиома или результат
применения продукционного правила к теореме (или теоремам).
Доказательством называется граф-дерево, корневая
вершина которого соответствует некоторой формуле, дуги – продукционным правилам, терминальные вершины – аксиомам.
Формула является теоремой тогда и только тогда, когда для неё существует доказательство.
Теорией (формальной теорией) называется множество всех теорем формальной системы.
Теории могут содержать как конечное, так и бесконечное число теорем.
Слайд 50Автоматы и языки
Пример.
Пусть есть некоторая грамматика G с множеством
правил P = {C → aC | bB;
A → aA
| bC; B → bB | с | cA }. Требуется построить конечный автомат А , распознающий цепочки языка L (G ). Какая грамматика ? Праворекурсивная.
Методика решения задачи.
Каждому нетерминалу грамматики G поставим в соответствие одно состояние конечного автомата A. Добавим еще одно состояние - единственное конечное состояние. Состояние, соответствующее аксиоме, назовем начальным состоянием.
Каждому правилу A→aB поставим в соответствие команду Aa → B, а каждому
терминальному правилу A → a поставим в соответствие команду Aa → F.
Таким образом, выводу цепочки в грамматике
взаимно однозначно соответствует последовательность команд построенного автомата A:
Таким образом, язык L ( G ) = L ( A ).
Слайд 51Автоматы и языки
Граф автомата будет иметь четыре вершины. Три из
них помечены
нетерминальными символами C, A, B. Четвертая вершина, помеченная символом
F, является единственным заключительным состоянием. Начальное состояние -вершина, соответствующая аксиоме C (она помечена зеленым).
Таблица переходов
Состояния
Символы
алфавита
Слайд 52Каждому правилу грамматики поставим в соответствие команду конечного автомата:
Ca →
C - в начальном состоянии при поступлении на вход терминального
символа а автомат остается в том же состоянии C;
Cb → B - из начального состояния при поступлении на вход терминала b автомат
переходит в состояние B;
Bb → B - в состоянии В при поступлении на вход терминала b автомат остается в том же состоянии B;
Bc → F - из состояния В при поступлении на вход терминала c автомат переходит в
заключительное состояние F;
Bc → A - из состояния В при поступлении на вход терминала c автомат переходит в
состояние А;
Aa → A - в состоянии А при поступлении на вход терминала а автомат остается в этом же состоянии А;
Ab → C - из состояния A при поступлении на вход терминала b автомат переходит в
состояние C.
Полученный недетерминированный конечный автомат распознает цепочки языка,
порождаемые праворекурсивной грамматикой G.
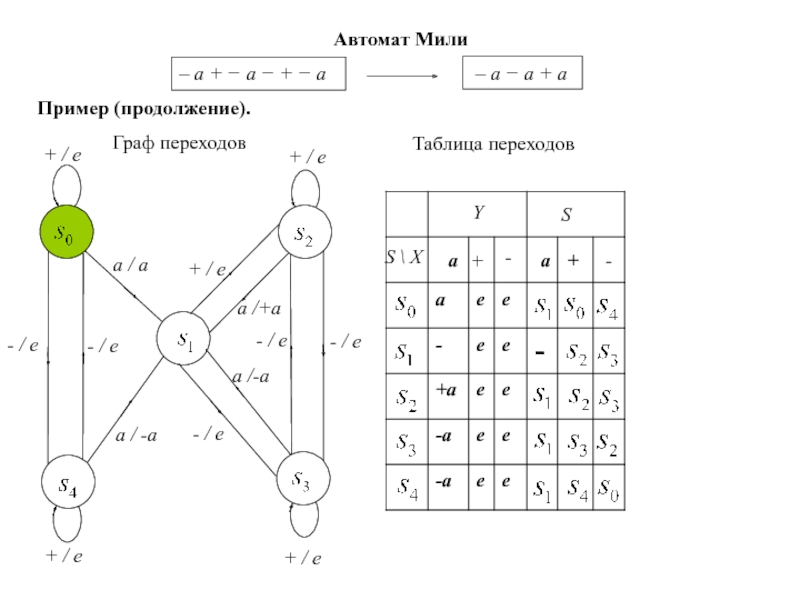
Слайд 57Автомат Мили
Пример (продолжение).
+ / e
+ / e
+ / e
+ /
e
a / a
+ / e
- / e
- / e
a /
-a
- / e
- / e
a /+a
- / e
a /-a
Y
S
S \ X
a
+
-
-
+
a
Граф переходов
Таблица переходов
– а − а + а
– a + − а − + − а
Слайд 58Преобразователь М начинает работу в состоянии и, чередуя
состояния и
на входном символе « − », определяет, четное или нечетное число знаков « − » предшествует первому символу а . Когда появляется а, преобразователь М переходит в состояние , допуская вход, и выдает а или − а в зависимости от того, четно или нечетно число появившихся минусов. Для следующих символов а он подсчитывает, четно или нечетно число предшествующих минусов, с помощью состояний и . Единственное различие между парами и состоит в том, что если символу а предшествует четное число минусов, то первая из них выдает +а , а не только а .
Автомат Мили
Слайд 59Автомат Мура
Автомат Мура - это «пятерка» вида:
U =
S, X, Y, f, h > ,
где S -
множество состояний автомата; X - входной алфавит; Y - выходной алфавит; f - функция переходов (отображение S X → S); h - функция выходов (отображение S X → Y).
При представлении автомата Мура графом дуги помечаются символами входного
алфавита, а каждая вершина графа - состоянием и символом выходного алфавита.
В автомате Мура реализована иная временная связь между переходами из одного
состояния в другое и выходом, по сравнению с автоматом Мили, у которого выход, соответствующий некоторому входу и определенному состоянию, порождается во время перехода автомата в следующее состояние. У автомата Мура сначала порождается выход, а потом - переход в следующее состояние, причем выход определяется только состоянием автомата.
Слайд 60Курт Гёдель, австрийский математик, доказал теорему и неполноте, основатель теории
алгоритмов
Стивен Клини, американский логик, математик, основоположник теории рекурсивных функций
Алонзо Черч,
профессор, американский математик и логик, основоположник теории алгоритмов, разработка лямбда-исчисления
Основоположники теории алгоритмов
Слайд 61Эмиль Пост,
польско-американский математик, основоположник теории алгоритмов, машина Поста, продукционные
систем ы Поста
Андрей Андреевич Марков,
член-корреспондент АН СССР, математик, существенный вклад
в теорию алгоритмов, нормальные алгоритмы Маркова
Алан Тьюринг, английский математик, криптограф, основоположник теории алгоритмов, машины Тьюринга
Основоположники теории алгоритмов
Слайд 62Теория алгоритмов — наука, изучающая общие свойства и закономерности алгоритмов и разнообразные
формальные модели их представления.
Задачи теории алгоритмов: формальное доказательство алгоритмической
неразрешимости задач, асимптотический анализ сложности алгоритмов, классификация алгоритмов в соответствии с классами сложности, разработка критериев сравнительной оценки качества алгоритмов и т. п.
Понятие теории алгоритмов
Слайд 63История возникновения теории алгоритмов
Развитие теории алгоритмов начинается с доказательства Куртом Гёделем теорем
о неполноте формальных систем, включающих арифметику, первая из которых была
доказана в 1931 г. В связи с этим было высказано предположение о невозможности алгоритмического решения многих математических задач и возникла потребность в стандартизации понятия алгоритм.
Первые стандартизованные варианты понятия алгоритм (модели алгоритмов) были разработаны в 30-х годах XX века в работах Алана Тьюринга, Алонзо Чёрча, Эмиля Поста. Основываясь на работах Гёделя, Стивен Клини ввел понятие рекурсивной функции.
Десятью годами позже Андрей Андреевич Марков ввел еще одну модель – нормальный алгоритм.
Значительный вклад в теорию алгоритмов внесли Алексей Андреевич Ляпунов, Дональд Кнут, Альфред Ахо, Джеффри Ульман.
Слайд 64Введение
Понятие алгоритма, являющееся одним из основных понятий математики, возникло задолго
до появления ЭВМ. На протяжении многих веков люди пользовались интуитивным
понятием алгоритма.
Арабский математик девятого века Мухаммед ибн Муса Аль Хорезми впервые выдвинул идею о том, что решение любой поставленной математической и философской задачи может быть оформлено в виде последовательности механически выполняемых правил, т.е. может быть алгоритмизировано
Этого же мнения придерживались Рене Декарт, Готфрид Лейбниц и, Давид Гильберт.
Рене Декарт,
французский математик, физик
Давид Гильберт,
выдающийся немецкий математик
Готфрид фон Лейбниц,
немецкий математик, философ
Слайд 65Определение понятия «алгоритм»
Алгоритм – это конечный набор четких, недвусмысленных инструкций,
следуя которым можно по входным данным определенного вида получать на
выходе некоторый результат.
Примеры.
Алгоритм сложения чисел в столбик. Если два натуральных числа в десятичной записи, то, следуя известному алгоритму, изучаемому в начальной школе, можно получить десятичную запись их суммы.
Алгоритмы построения циркулем и линейкой, изучаемые в средней школе. Например, алгоритм нахождения середины отрезка или алгоритм построения биссектрисы заданного угла.
Алгоритм решения квадратных уравнений. Подставляя в известную со школы формулу коэффициенты уравнения, можно вычислить количество его корней и сами корни (если они есть).
Слайд 66Математик и артиллерист
Артиллерист
Математик
Программист
Физик сказал мне, что полет тела в атмосфере
подчиняется таким-то и таким-то законам. Дайте мне формулу, я подставлю
в нее массу снаряда, начальную скорость, угол наклона ствола и определю куда попадет снаряд.
Вынужден тебя огорчить, формулы не существует. Вот тебе алгоритм, иди к программисту, он напишет программу. Будешь вводить исходные данные и она будет вычислять координаты падения снаряда с некоторой точностью.
Дело сделано. А зачем мне нужен был математик? Ах да. Он дал мне алгоритм !
Слайд 67На ранних этапах своего развития математика была ничем иным, как
набором алгоритмов «на все случаи жизни».
Сегодняшняя математика – это
скорее набор теорем, а не набор алгоритмов.
Для конечного потребителя «математического продукта» математика по- прежнему – набор алгоритмов. Алгоритмы – это «продукт» математики, как древней, так и современно, то, что она дает на выходе.
Алгоритмы и математика
Слайд 68Алгоритмы и математика
Математик сделал свое дело. Он сидел, погружаясь в
абстракции, строил гипотезы, доказал пару теорем, а в результате выдал
… алгоритм. Алгоритмы важны для математики. Они ее конечный продукт, оправдывающий присутствие этой науки во «внешнем мире».
Теоремы и леммы никому, кроме самих математиков , не нужны. Если бы еще и алгоритмы никого кроме математиков не интересовали, тот тогда математикой могли бы заниматься лишь обеспеченные люди, которые могут позволить себе эту роскошь.
Ситуация намеренно упрощена. Математика – это язык науки. Значит алгоритмы – это язык математика и его нужно знать.
Слайд 69Математик и артиллерист (продолжение)
Ничего не могу придумать. Задача очень сложная.
Буду думать еще.
Я тут провел исследования и доказал, что алгоритма
для решения Вашей задачи не существует.
Еще два варианта ответа математика артиллеристу.
Слайд 70Неразрешимые математические задачи
Известно множество примеров задач, для которых не существует
алгоритма их решения. Бывают ситуации, когда алгоритм, возможно, и есть,
но найти его экономически нецелесообразно (например, мало на это времени и средств).
В первом случае задачи называют «неразрешимые задачи».
Во втором случае задачи называют «слабоструктурированные, трудноформализуемые задачи».
Слайд 71Задача удвоения куба
К неразрешимым задачам математика относит задачи на построение
при помощи циркуля и линейки: удвоение куба, трисекция угла и
квадратура круга.
Задача удвоения куба. Это классическая задача древности о построении куба, имеющего объем вдвое больший, чем данный куб. Эту задачу называют еще и делийской (делосской), так как по преданию, для избавления от чумы на острове Делос в Эгейском море, оракул потребовал вдвое увеличить кубической формы жертвенник не меняя его формы. Задача сводится к построению отрезка, численно равного , что , как было доказано в 19 веке, не может быть выполнено при помощи циркуля и линейки. При построении подобного отрезка объем полученного куба будет превышать объем исходного ровно в два раза, так как
Слайд 72Задачи на квадратуру круга и трисекцию угла
Квадратура круга. Это задача
о разыскании квадрата, равновеликого данному кругу.
Трисекция угла. Это задача выделения
с помощью циркуля и линейки угла в три раза меньшего, чем исходный угол.
Справедливости ради отметим, что в своей книге к.ф-м. н., доцент Виталий Комиссаров: из г. Астрахани: «В.С. Комиссаров. Три задачи древности. Удвоение куба. Квадратура круга. Пентаграмма Стоунхенджа. Трисекция угла.- Астрахань: Изд-во «АЦТ», 2009.- 76 с.» дает алгоритмическое решение всех трех задач.
Слайд 73Свойства алгоритмов
Каждый алгоритм имеет дело с данными – входными, промежуточными
и выходными. Данные как объекты, с которыми могут работать алгоритмы,
должны быть четко определены и отличимы как друг от друга, так и от другой информации. Данные для своего размещения требуют памяти. Память считается однородной и дискретной. Единицы измерения объема данных и памяти согласованы. Память может быть бесконечной.
Если выполнение алгоритма заканчивается получением результатов, то говорят, что он применим к исходным данным. Применимый алгоритм имеет следующие свойства, раскрывающие его определение:
Дискретность. Алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Для выполнения каждого шага требуется конечный отрезок времени.
Определенность (детерминированность). Каждое правило алгоритма должно быть четким и однозначным. Отсюда выполнение6 алгоритма носит механический характер.
Результативность (конечность). Алгоритм должен приводить к решению задачи за конечное число шагов.
Массовость. Алгоритм решения задачи разрабатывается в общем виде и должен быть применим для некоторого класса задач, различающихся лишь исходными данными.

Слайд 74Задание алгоритма
Чтобы задать алгоритм необходимо выделить и описать следующие его
элементы:
Набор объектов, составляющих совокупность данных: исходных, промежуточных и конечных.
Правило начала.
Правила непосредственной переработки информации.
Правило окончания.
Правило извлечения результатов.
Алгоритм всегда рассчитан на конкретного исполнителя. Если исполнитель – компьютер, то алгоритм должен быть записан на языке программирования.
Слайд 75Математическое определение алгоритма
Алгоритм – конструктивно задаваемое соответствие между изображениями объектов
в абстрактных алфавитах.
Алгоритм – четкая конечная система правил для преобразования
слов из некоторого алфавита в слова из этого же или другого алфавита.
Четыре основных универсальных алгоритмических модели (системы) :
Рекурсивные функции. Исторически первая формализация понятия алгоритма. Она связывает понятие алгоритма с математическими объектами: вычислениями и числовыми функциями.
Машины Тьюринга. Алгоритм представляется как детерминированное устройство, способное выполнять в каждый отдельный момент некоторые примитивные операции или инструкции. Это автоматная модель алгоритмов.
Нормальные алгоритмы А.А. Маркова. Алгоритм представляется как преобразователь слов в произвольных алфавитах с использованием операции подстановки, т.е. замены части слова на другое слово.
Лямбда-исчисление. Это класс лямбда-определяемых функций, который в точности характеризует понятие эффективной вычислимости и тем самым формализует понятие алгоритма.
Слайд 76Нормальные алгоритмы Маркова
Понятие нормального алгоритма
Слайд 77Нормальные алгоритмы Маркова
Понятие нормального алгоритма
Для организации последовательного использования правил все
они должны быть индексированы
. Совокупность индексированных правил называется протоколом (схемой):
Слайд 78Нормальные алгоритмы Маркова
Понятие нормального алгоритма
В схеме есть простые правила, которые
обозначаются как
и
заключительные: .
Суть упорядоченного использования правил из схемы состоит в том, что каждое переработанное слово вновь поступает в начало алгоритма и вновь проверяется на возможность подстановки. Так будет до тех пор, пока ни одно из правил подстановки не может быть использовано, а заключительной подстановкой будет дано указание об окончании работы алгоритма.
Если окажется, что ни одно из правил не применимо, то это означает ситуацию «тупик».
Слайд 79Нормальные алгоритмы Маркова
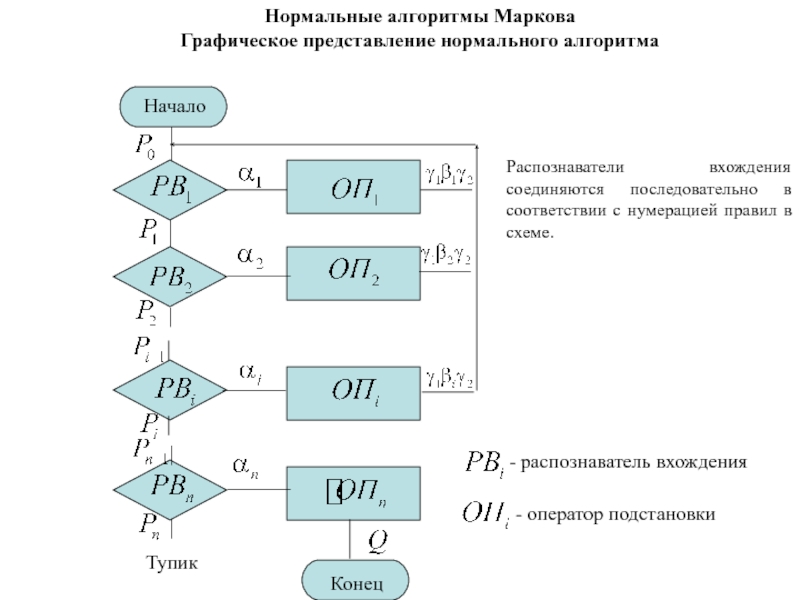
Графическое представление нормального алгоритма
Начало
Конец
Тупик
- распознаватель вхождения
- оператор подстановки
Распознаватели
вхождения соединяются последовательно в соответствии с нумерацией правил в схеме.
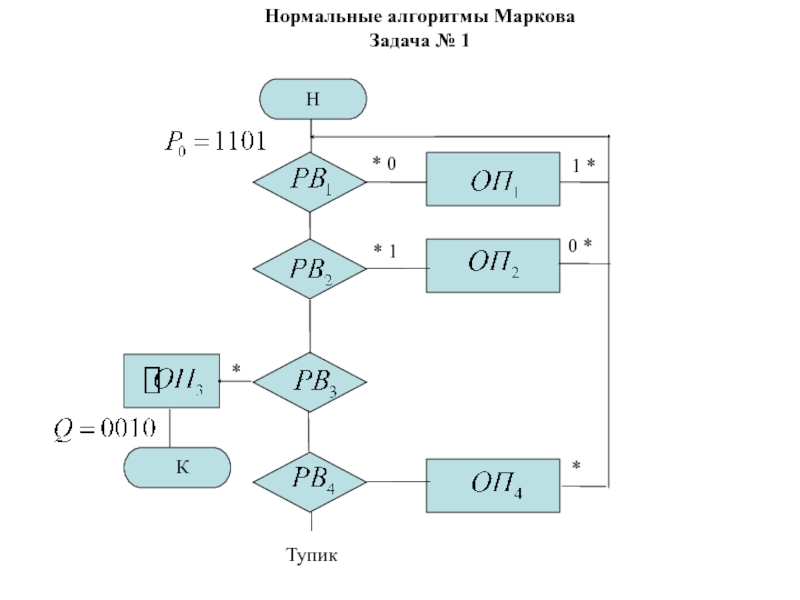
Слайд 80Задача 1 – «Инверсия цифр». Задана строка из нулей и
единиц. Получить на выходе строку, в которой единицы заменены нулями,
а нули – единицами.
Нормальные алгоритмы Маркова
Задача № 1.
Ниже приведена схема нормального алгоритма. При этом .
Схема:
* 0 → 1 *
* 1 → 0 *
* → .
→ *
Работник « * » двигается вдоль строки и выполняет работу меняя 0→1, 1→0
Уничтожение работника. Останов
Включение работника в строку (замена пустой строки на *)
Слайд 81Н
Тупик
К
* 1
* 0
1 *
0 *
*
Нормальные алгоритмы
Маркова
Задача № 1
*
Слайд 82Нормальные алгоритмы Маркова
Задача № 1
Схема:
1) * 0 → 1 *
2)
* 1 → 0 *
3) * → .
4)
→ *
Слайд 83Нормальные алгоритмы Маркова
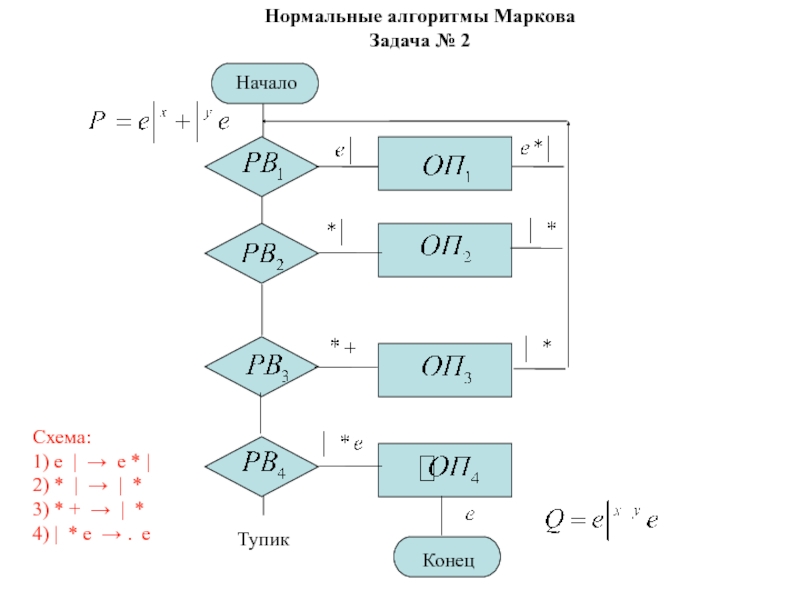
Задача № 2
Задача 2 – «Вычисление суммы двух
чисел в унарном коде». Даны два десятичных числа, представленные в
унарном коде. Найти их сумму в унарном коде.
Понятие унарного кода
Слайд 84Нормальные алгоритмы Маркова
Задача № 2
Пусть есть два числа x и
y.
В унарном коде (без нуля) они запишутся как
и .
Их сумма запишется как .
Тогда в задаче № 2 , а .
Алфавит .
Схема:
e | → e * |
* | → | *
* + → | *
| * e → . e
Слайд 85Нормальные алгоритмы Маркова
Задача № 2
Начало
Конец
Тупик
Схема:
1) e | → e *
|
2) * | → | *
3) * + → |
*
4) | * e → . e
Слайд 86Нормальные алгоритмы Маркова
Задача № 2
Пусть x = 2 и
y = 3 .Тогда имеем вычислительный процесс
преобразования исходного слова
в
заключительное :
Схема:
1) e | → e * |
2) * | → | *
3) * + → | *
4) | * e → . e
Слайд 87Нормальные алгоритмы Маркова
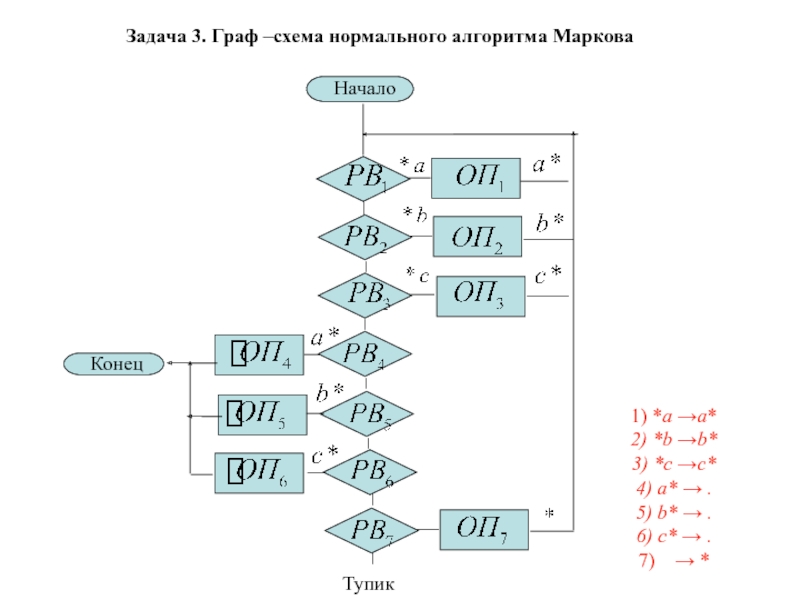
Задача № 3
Задача №3. Пусть А = {a,b,c}.
Удалить из непустого слова P его последний символ.
Протокол:
*a →a*
*b →b*
*c
→c*
a* → .
b* → .
c* → .
→ *
Слайд 89Пусть P=еaabcaе и Q=еaabcе .Тогда имеем вычислительный процесс
преобразования
исходного слова P в заключительное Q:
:
Нормальные алгоритмы Маркова
Задача № 3
1) *a →a*
2) *b →b*
3) *c →c*
4) a* → .
5) b* → .
6) c* → .
7) → *
Слайд 90Определение нормального алгоритма
Нормальными алгоритмами называются алгоритмы, составленные только из распознавателей
входных слов и операторов подстановки, граф-схемы которых удовлетворяют следующим условиям:
Все узлы-распознаватели упорядочиваются нумерацией от 1 до N.
Дуги, исходящие из узлов, соответствующих операторам подстановки, подсоединяются либо к узлу первого распознавателя, либо к выходному узлу. В первом случае подстановка называется обычной, во втором – заключительной.
Входной узел подсоединяется дугой к первому распознавателю.
Слайд 91Граф-схема нормального алгоритма Маркова
Вход
Выход
Слайд 92Универсальность нормальных алгоритмов
Универсальность нормальных алгоритмов формулируется в виде принципа нормализации:
«Для
любого алгоритма (конструктивно задаваемого алфавитного отображения) в произвольном конечном алфавите
А можно построить эквивалентный ему нормальный алгоритм над алфавитом А ».
Иногда не удается построить нормальный алгоритм, эквивалентный данному алгоритму в алфавите A . Однако можно построить требуемый нормальный алгоритм, добавив к алфавиту некоторое количество букв.
Если нормальный алгоритм задан в расширенном алфавите А, то говорят, что нормальный алгоритм задан над алфавитом.
Слайд 93Машины Тьюринга
Основные свойства алгоритма дискретности, детерминизма,
массовости и результативности позволяют представить процесс вычисления какой-либо числовой функции
с помощью математической машины. Эта машина за конечное число шагов из исходных числовых данных в соответствии с заданными правилами может получить искомый числовой результат.
Такая модель алгоритма была предложена английским математиком Тьюрингом в конце 30-х годов прошлого столетия, что почти на два десятилетия опередило появление электронных вычислительных машин и послужило их теоретическим прообразом.
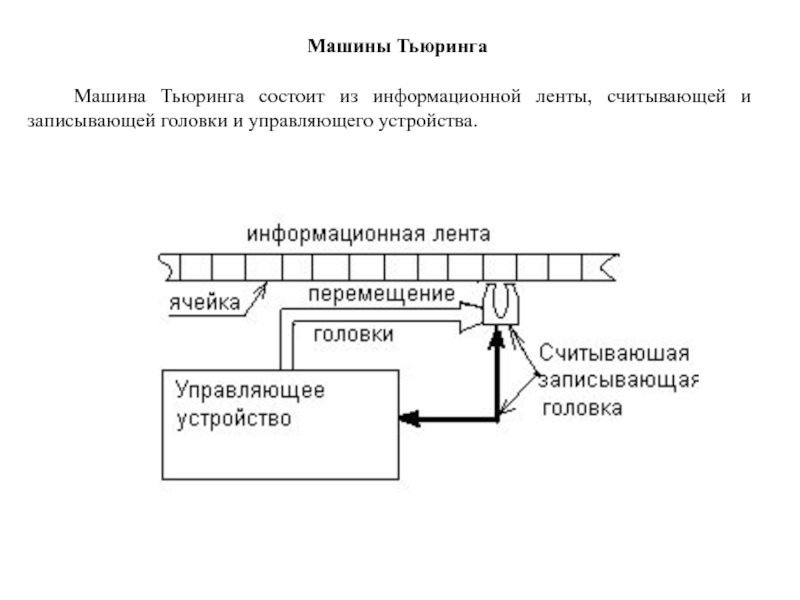
Слайд 94Машины Тьюринга
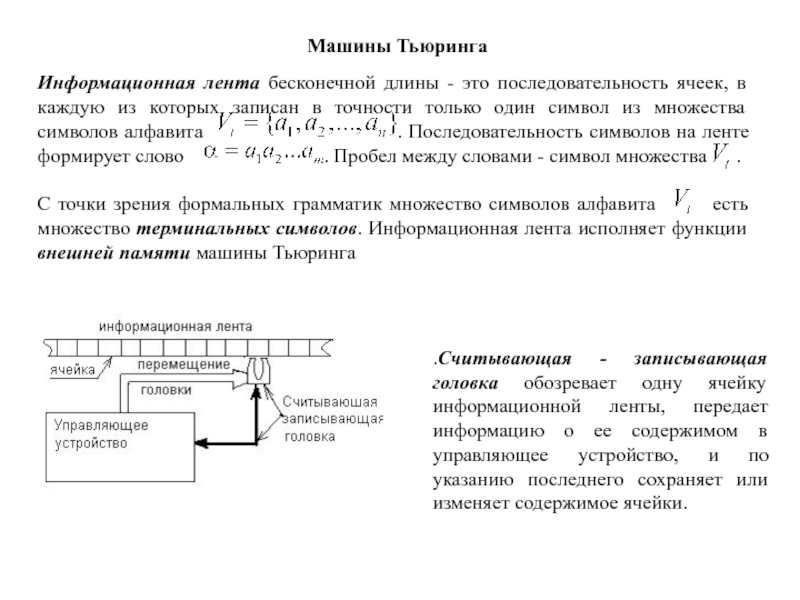
Машина Тьюринга состоит из информационной ленты, считывающей и записывающей
головки и управляющего устройства.
Слайд 95Машины Тьюринга
.Считывающая - записывающая головка обозревает одну ячейку информационной ленты,
передает информацию о ее содержимом в управляющее устройство, и по
указанию последнего сохраняет или изменяет содержимое ячейки.
Слайд 96Понятие "состояние" формирует "память машины Тьюринга. Поэтому множество состояний управляющего
устройства называют внутренней памятью машины Тьюринга.
Машины Тьюринга
Слайд 97Машина Тьюринга
Для формализации перемещений головки относительно информационной ленты введем дополнительный
алфавит D = {П, Л, С}, где П — означает
перемещение головки вправо на одну ячейку информационной ленты, Л — влево на одну ячейку и С — останов.
Работа машины Тьюринга состоит в многократном повторении следующего цикла элементарных действий:
действие первое: считывание символа , находящегося под считывающей головкой;
действие второе: поиск команды, отвечающей текущему состоянию управляющего устройства , и считанному символу , т.е.
действие третье: исполнение найденной команды, т.е. запись в обозреваемую ячейку символа , перевод управляющего устройства в состояние и перемещение головки на соседнюю ячейку информационной ленты D.
Эти три действия формируют элементарный шаг алгоритмического процесса.
Последовательность команд для реализации процесса вычисления формирует протокол машины Тьюринга или программу алгоритмического процесса.
Слайд 100Машина Тьюринга
Описание машины Тьюринга
Слайд 101Машина Тьюринга
Понятие полуленты
Для упорядочения составления протоколов информационную ленту ограничивают только
в одну сторону, т. е. существуют левые и правые полуленты.
В зависимости от используемой полуленты приняты различные схемы записи конфигураций машины Тьюринга.
Слайд 102Машина Тьюринга
Способы определения машины Тьюринга
Для определения работы машины Тьюринга применяют:
Протокольное
представление;
Табличное представление;
Графовое представление
При протокольной записи все команды должны быть
записаны упорядоченным списком. На заключительном шаге должно быть получено выходное слово. .
Например,
Протокольное представление
Слайд 103Машина Тьюринга
Способы определения машины Тьюринга
При табличном описании каждая строка имеет
имя текущего состояния машины, а столбец–имя символа внешней памяти. Тогда
элементами таблицы являются правые части команд .
Табличная форма описания машины более компактна и позволяет применить матричные методы анализа для оптимизации структуры алгоритма.
Слайд 104Машина Тьюринга
Способы определения машины Тьюринга
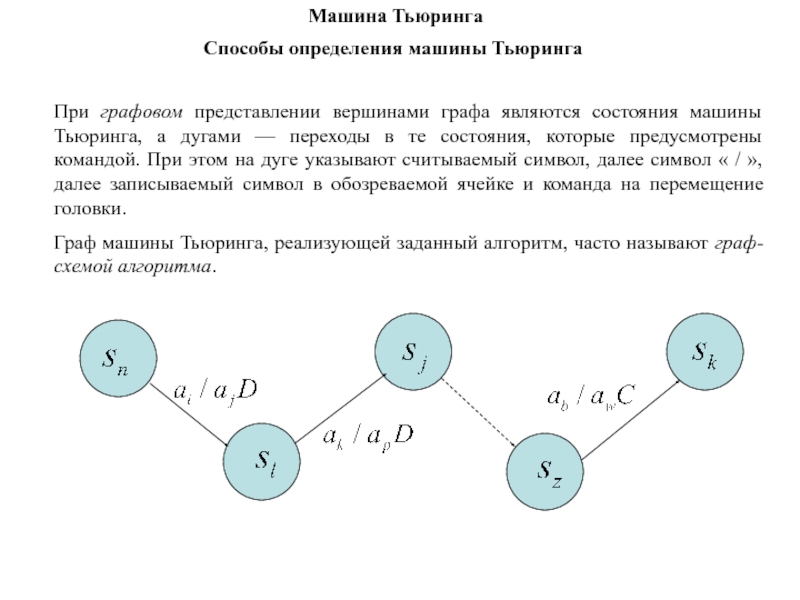
При графовом представлении вершинами графа являются
состояния машины Тьюринга, а дугами — переходы в те состояния,
которые предусмотрены командой. При этом на дуге указывают считываемый символ, далее символ « / », далее записываемый символ в обозреваемой ячейке и команда на перемещение головки.
Граф машины Тьюринга, реализующей заданный алгоритм, часто называют граф-схемой алгоритма.
Слайд 105Реализация на машине Тьюринга примитивно-рекурсивных функций
Задача 1. Разработать алгоритм, реализующий
вычисление значений функции следования V(x) = x + 1 на
правой полуленте:
Протокол.
Граф-схема
Таблица переходов
Слайд 106Пусть x = 3, т.е. V (3) = 4 и
имеем следующий вычислительный процесс:
Реализация на машине Тьюринга примитивно-рекурсивных функций
Протокол
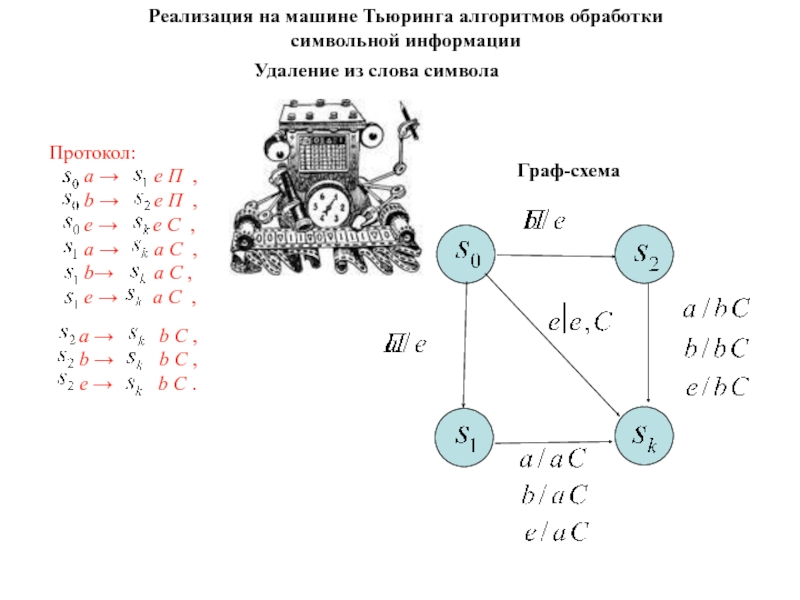
Слайд 107Реализация на машине Тьюринга алгоритмов обработки символьной информации
Задача 2 –
«Удаление из слова символа». А = {a,b}. Удалить из слова
Р его второй символ, если такой есть.
Решение. Казалось бы, эту задачу решить просто: надо переместить головку под клетку со вторым символом и затем очистить эту клетку:
е
Однако в выходном слове Q не должно быть пустых клеток. Поэтому после удаления 2-го символа надо «сжать» слово, перенеся первый символ на одну клетку вправо. Для этого головку нужно вернуть к первому символу, запомнить его и стереть, а затем, снова сдвинувшись вправо, записать его в клетку, где был 2-ой символ. Однако начальный «поход» вправо ко второму символу, чтобы его стереть, и последующий возврат к первому символу - лишние действия. Поэтому сразу запоминаем первый символ, стираем его и записываем вместо второго символа. Остановить перемещение головки при достижении конечного состояния.
Слайд 108Протокол (продолжение):
а →
b C ,
b →
b C ,
e → b C .
Реализация на машине Тьюринга алгоритмов обработки символьной информации
Удаление из слова символа
Слайд 109Граф-схема
Реализация на машине Тьюринга алгоритмов обработки символьной информации
Удаление из слова
символа
а →
b C ,
b → b C ,
e → b C .
Слайд 110Описание вычислительного процесса
Реализация на машине Тьюринга алгоритмов обработки символьной информации
P = eaabbae
e a a b b a e e e a b b a e e e a b b a e
Имеем следующий вычислительный процесс:
P = ebbe
e b b e e e b e e e b e
Слайд 111Реализация на машине Тьюринга алгоритмов обработки символьной информации
Задача 3 –
«Формирование слова на новом месте». А = {a,b,с}. Удалить из
Р все вхождения символа а .
Решение. В машине Тьюринга сложно реализуются вставки символов в слова и удаления символов из слов. Проще не раздвигать или сжимать входное слово, а формировать выходное слово в другом, свободном месте ленты. Для этого выполним следующие действия:
1.Выходное слово строим справа от входного. Чтобы разграничить эти слова, отделим их символом (пусть это будет « = » ) - действие 1 .
2.После этого возвращаемся к началу входного слова – действие 2.
3. Переносим в цикле все символы входного слова, кроме a , вправо за знак « = » в формируемое выходное слово. Для этого анализируем первый символ входного слова. Если это a , тогда стираем его и переходим к следующему символу. Если же первый символ – это b или c, тогда стираем его и «бежим» вправо до первой пустой клетки, куда и записываем этот символ – действия 3 - 5.
Слайд 112Снова возвращаемся налево к тому символу, который стал первым во
входном слове, и повторяем те же самые действия, но уже
по отношению к этому символу – действия 6 -9.
4. Этот цикл завершается, когда при возврате налево увидим в качестве первого символа знак « = ». Это признак полного просмотра входного слова и переноса всех его символов, отличных от a , в выходное слово. Надо этот знак стереть, сдвинуться вправо под выходное слово и остановиться – действие 10.
Реализация на машине Тьюринга алгоритмов обработки символьной информации
Слайд 113Реализация на машине Тьюринга алгоритмов обработки символьной информации
Таблица для задачи
Слайд 114Представление информации. Системы счисления
Системой счисления называется совокупность приемов наименования и
записи чисел. В любой системе счисления для представления чисел выбираются
некоторые символы (их называют цифрами), а остальные числа получаются в результате каких-либо операций над цифрами данной системы счисления.
Система называется позиционной, если значение каждой цифры (ее вес) изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.
Число единиц какого-либо разряда, объединяемых в единицу более старшего разряда, называют основанием позиционной системы счисления. Если количество таких цифр равно P, то система счисления называется P-ичной. Основание системы счисления совпадает с количеством цифр, используемых для записи чисел в этой системе счисления.
Запись произвольного числа x в P-ичной позиционной системе счисления основывается на представлении этого числа в виде многочлена
Слайд 115Системы счисления
Запись произвольного числа m в P-ичной позиционной системе счисления
основывается на представлении этого числа в виде многочлена:
Слайд 116Системы счисления
Таблица двоичных чисел до семи
Переводы из одной системы счисления
в другую
Выполнение арифметических действий в системах счисления
Слайд 117Двоичная система счисления
Двоичная система счисления – компьютерный соперник десятичной. С
теоретической точки зрения двоичная система счисления выделяется тем, что ее
основание 2 - наименьшее возможное. В этой системе только две цифры -1 и 0.
Двоичная система счисления была придумана математиками и философами ещё до появления компьютеров (XVII — XIX вв.). Выдающийся математик Лейбниц говорил: "Вычисление с помощью двоек... является для науки основным и порождает новые открытия... При сведении чисел к простейшим началам, каковы 0 и 1, везде появляется чудесный порядок". Позже двоичная система была забыта, и только в 1936 — 1938 годах американский инженер и математик Клод Шеннон нашёл замечательные применения двоичной системы при конструировании электронных схем.
Слайд 118
Каждая цифра, буква, символ в памяти компьютера кодируется двоичным числом.
Один
разряд двоичного числа называется бит (англ. «маленький»)
Для обозначения какого-нибудь
символа (цифры, буквы, запятой, точки...) в компьютере используется определенное количество бит. Компьютер "распознает" 256 (от 0 до 255) различных символов по их коду. Этого достаточно, чтобы вместить все цифры (0 - 9), буквы латинского алфавита (a - z, A - Z), русского (а - я, А - Я), а также другие символы.
Для представления символа с максимально возможным кодом (255) нужно 8 бит. Эти 8 бит называются байтом.
Т.о. один любой символ - это всегда 1 байт.
Хранение данных в памяти компьютера
Слайд 119
ANSI (англ. American National Standards Institute) –8-битной кодировкой, которая может
представлять только 256 уникальных символов.
UNICODE - 16-разрядная кодировка, что
обеспечивает 65 536 уникальных символов - более чем достаточно для представления всех языков мира. Он поддерживает даже архаические языки, такие как санскрит и египетские иероглифы, и включает знаки препинания, математические и графические символы.
Родной кодировкой для Windows XP является Unicode, но она поддерживает и ANSI.
Стандарты кодировки
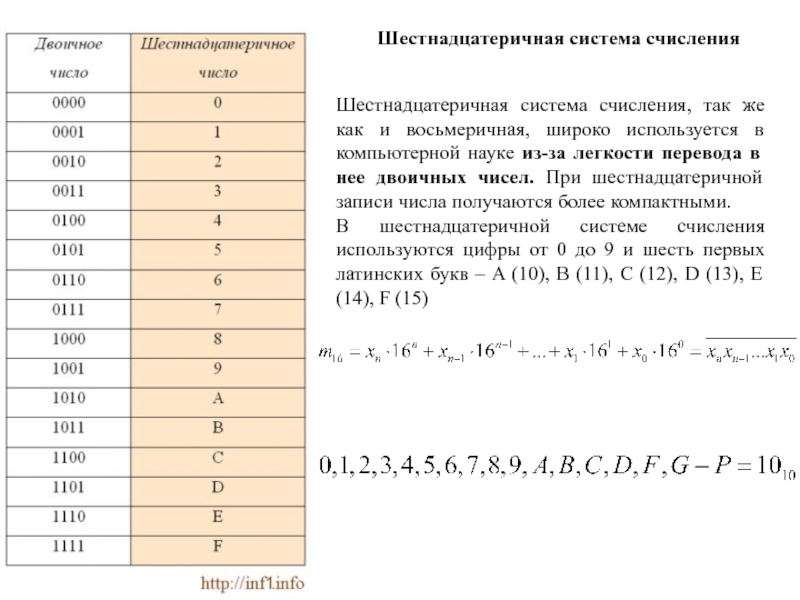
Слайд 120Шестнадцатеричная система счисления, так же как и восьмеричная, широко используется
в компьютерной науке из-за легкости перевода в нее двоичных чисел.
При шестнадцатеричной записи числа получаются более компактными.
В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв – A (10), B (11), C (12), D (13), E (14), F (15)
Шестнадцатеричная система счисления
Слайд 121Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи
- это FF:
FF = 15 * 161 + 15 * 160 = 240 + 15 = 255
255 – это максимальное значение одного байта, равного 8 битам: 1111 1111 = FF.
Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов.
При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди. Каждой четверке соответствует цифра шестнадцатеричной системе счисления:
Например:
10001100101 = 0100 1100 0101 = 4 C 5 = 4C5
Если потребуется, то число 4C5 можно перевести в десятичную систему счисления следующим образом (C следует заменить на соответствующее данному символу число в десятичной системе счисления – это 12):
4C5 = 4 * 162 + 12 * 161 + 5 * 160 = 4 * 256 + 192 + 5 = 1221
Шестнадцатеричная система счисления
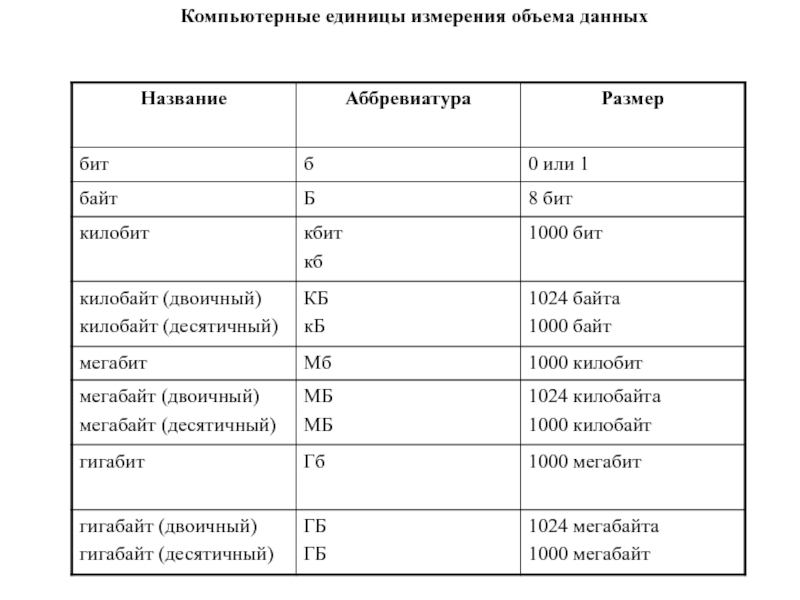
Слайд 123Компьютерные единицы измерения объема данных
Слайд 124Переводы из одной системы счисления в другую
1. Для перевода двоичного
числа в десятичное необходимо его записать в виде многочлена, состоящего
из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
:
Слайд 1252. Для перевода восьмеричного числа в десятичное необходимо его записать
в виде многочлена, состоящего из произведений цифр числа и соответствующей
степени числа 8, и вычислить по правилам десятичной арифметики
Переводы из одной системы счисления в другую
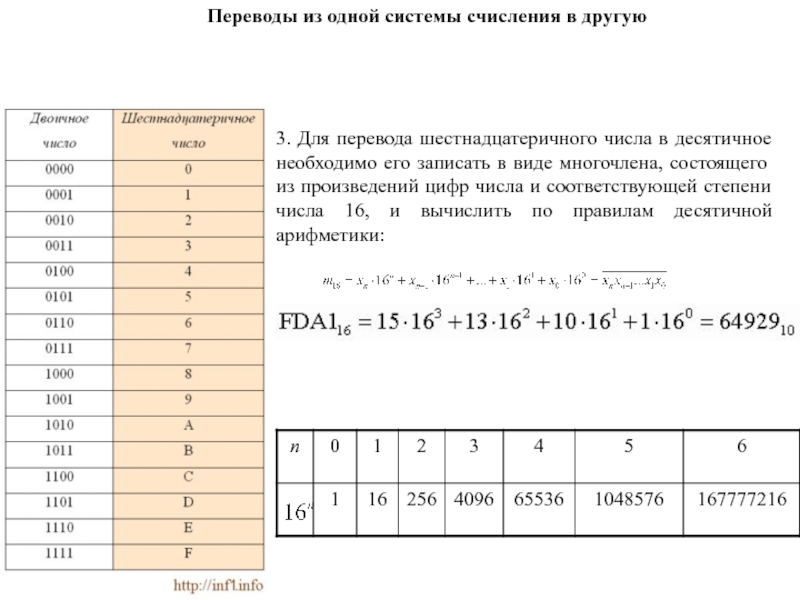
Слайд 1263. Для перевода шестнадцатеричного числа в десятичное необходимо его записать
в виде многочлена, состоящего из произведений цифр числа и соответствующей
степени числа 16, и вычислить по правилам десятичной арифметики:
Переводы из одной системы счисления в другую
Слайд 1274. Для перевода десятичного числа в двоичную систему его необходимо
последовательно делить на 2 до тех пор, пока не останется
остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Переводы из одной системы счисления в другую
Слайд 1285. Для перевода десятичного числа в восьмеричную систему его необходимо
последовательно делить на 8 до тех пор, пока не останется
остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Переводы из одной системы счисления в другую
Слайд 1296. Для перевода десятичного числа в шестнадцатеричную систему его необходимо
последовательно делить на 16 до тех пор, пока не останется
остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Переводы из одной системы счисления в другую
Слайд 1307. Чтобы перевести число из двоичной системы в восьмеричную, его
нужно разбить на триады (тройки цифр), начиная с младшего разряда,
в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой.
Переводы из одной системы счисления в другую
Слайд 1318.Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно
разбить на тетрады (четверки цифр), начиная с младшего разряда, в
случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой
9.Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.
10.Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.
11. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Переводы из одной системы счисления в другую
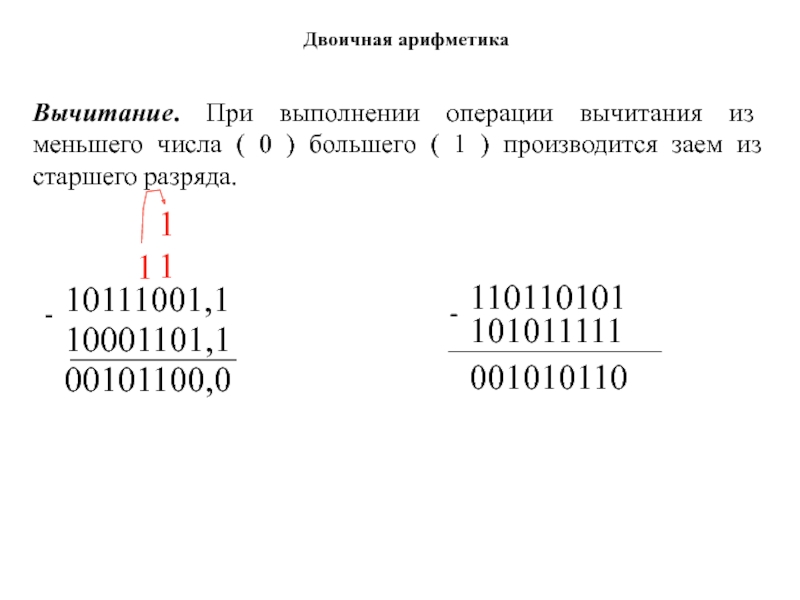
Слайд 132Сложение. Таблица двоичного сложения проста. Только в одном случае, когда
производится сложение 1+1, происходит перенос в старший разряд. В старший
разряд всегда переходит 1.
Слайд 136Восьмеричная арифметика
Таблица восьмеричного сложения
Таблица восьмеричного умножения
Слайд 138Основы кодирования информации
Кодирование - отображение сообщения по известным правилам.
Кодирование источников. Примеры: кодирование связанного текста кодом Морзе, оцифровка аудио
сигнала при записи на компакт диски. При кодировании источников избыточность сообщений снижается и такое кодирование часто называют сжатием данных.
Кодирование каналов увеличивает избыточность сообщений. Внесение дополнительных проверочных символов позволяет обнаруживать и исправлять ошибки, возникающие при передаче информации но каналу. Кодирование канала называется помехоустойчивым кодированием.
Без помехоустойчивого кодирования было бы невозможным создание накопителей огромной емкости, таких, как CD-ROM, DVD или жестких дисков. Дополнительные затраты на помехоустойчивое кодирование, обеспечивающее приемлемые вероятности ошибок записи/чтения, становятся пренебрежимо малыми по сравнению с выигрышем от достигаемой при этом плотности записи.
Слайд 139Основы кодирования информации
В 1948 г., опубликовав работу «Математическая теория связи»,
К. Шеннон дал определение понятий современной теории информации и заложил
основы техники связи.
Шеннон, в качестве примера, привел широко распространенные в то время перфокарты.
Слайд 140Перфока́рта (лат. perforo — пробиваю и лат.. charta — лист из папируса; бумага) —носитель информации, предназначенный для использования
в системах автоматической обработки данных. Сделана из тонкого картона, перфокарта представляет
информацию наличием или отсутствием отверстий в определённых позициях карты.
Перфокарты впервые начали применяться в ткацких станках Жаккарда (1808) для управления узорами на тканях. Существовало много разных форматов перфокарт; наиболее распространённым был «формат IBM», введённый в 1928 г.
Компьютеры первого, второго и частично третьего поколений, использовали перфокарты в качестве основного носителя при хранении и обработке данных.
Перфокарта – носитель информации
Слайд 141Перфоле́нта (перфорированная лента) — носитель информации в виде бумажной ленты с отверстиями. Первые перфоленты
использовались с середины X1X века в телеграфии, отверстия в них располагались
в 5 рядов, для передачи данных использовался код Бодо.
В середине ленты идёт дорожка с более мелкой перфорацией, так называемая «синхро дорожка». Она служит для перемещения ленты с помощью зубчатого колеса.
Благодаря простоте устройств ввода/вывода, перфолента получила распространение в компьютерной технике. Поздние компьютерные перфоленты имели ширину 7 или 8 рядов и использовали для записи кодировку ASC11. Были вытеснены магнитными носителями информации.
Перфолента – носитель информации
ASCII (англ. American Standard Code for Information Interchange) —американский стандартный код для обмена информацией
Слайд 142Основы кодирования информации
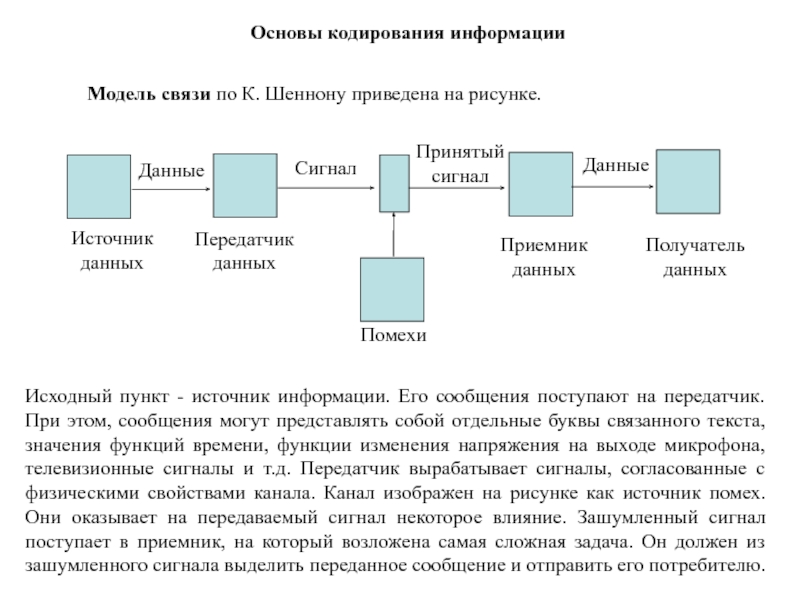
Модель связи по К. Шеннону приведена на рисунке.
Источник
данных
Передатчик данных
Приемник данных
Получатель данных
Помехи
Данные
Сигнал
Принятый сигнал
Данные
Исходный пункт - источник информации. Его
сообщения поступают на передатчик. При этом, сообщения могут представлять собой отдельные буквы связанного текста, значения функций времени, функции изменения напряжения на выходе микрофона, телевизионные сигналы и т.д. Передатчик вырабатывает сигналы, согласованные с физическими свойствами канала. Канал изображен на рисунке как источник помех. Они оказывает на передаваемый сигнал некоторое влияние. Зашумленный сигнал поступает в приемник, на который возложена самая сложная задача. Он должен из зашумленного сигнала выделить переданное сообщение и отправить его потребителю.
Слайд 143Основы кодирования информации
Информация одного события
Обмен информацией, несмотря на свою нематериальную
природу - неотъемлемая частью нашей жизни. Норберт Виннер, один из
основателей современной теории информации, охарактеризовал информацию следующим образом:
«Информация есть информация, а не материя или энергия».
Мы говорим: «Эта информация для меня важна», имея в виду конкретную ситуацию. Такое субъективное восприятие не подходит для технического представления информации. Как строго научное понятие, информация введена в технику в качестве измеряемой величины (аналогично длине в метрах, напряжению в вольтах и т.д.).
Повседневный опыт говорит о том, что, принимая информацию к сведению, мы постоянно устраняем некоторую неопределенность. Это очень напоминает эксперименты со случайными событиями. Проводя такие эксперименты, мы наблюдаем случайные события и это снижает неопределенность системы.
Формула Хартли
Формула Шеннона
Слайд 144Понятие энтропии
В термодинамике известна мера хаоса, беспорядка в системе
где
H - энтропия системы, k - коэффициент Больцмана, известный в
физике как k = 1.38×10-16 эрг/град.
Сравнивая выражения I и H
видим, что I можно понимать как информационную энтропию (энтропию из-за нехватки информации о/в системе). Л. Больцман дал статистическое определение энтропии в 1877 г. и заметил, что энтропия характеризует недостающую информацию. Спустя 70 лет, К. Шеннон сформулировал постулаты теории информации, а затем было замечено, что формула Больцмана инвариантна информационной энтропии, и была выявлена их системная связь, системность этих фундаментальных понятий.
Слайд 145Понятие энтропии
Нулевой энтропии соответствует максимальная информация. Основное соотношение между энтропией
и информацией:
или в дифференциальной форме
При переходе системы из состояния
с информацией к состоянию с информацией возможны случаи:
- уничтожение (уменьшение) старой информации в системе;
2. - сохранение информации в системе;
3 - рождение новой (увеличение) информации в системе.
Слайд 146Кодирование информации
Разложение процесса выбора символов
Шеннон показал, что любое событие, содержащееся
в источнике, может быть разложе-
но на последовательности двоичных решений с
исходами «да» или «нет» без потери информации.
Рассмотрим три события a, b и с. которые происходят с вероятностями 1/2,1/3 и 1/6, соответственно.
1/2
1/3
1/6
a
b
c
1/2
b
1/2
a
1/6
1/3
Преобразование в двоичное дерево
Для того, чтобы выбрать одно из этих трех, мы можем ставить два независимых вопроса.
Да (1)
Нет (0)
Да (1)
Нет (0)
Слайд 147Кодирование информации
Каждому событию, содержащемуся в алфавите, может быть приписана некоторая
последовательность двоичных символов «0» или «1» . Такую последовательность будем
называть кодовым словом события. При этом не происходит потери информации, так как каждое событие может быть непосредственно восстановлено по соответствующему кодовому слову. Такой процесс называется кодированием источника, а совокупность кодовых слов всех событий - кодом источника.
Слайд 148Учитывая статистические свойства источника сообщения, можно минимизировать среднее число двоичных
символов, требующихся для выражения одной буквы сообщения, что при отсутствии
шума позволяет уменьшить время передачи или объем запоминающего устройства. Такое эффективное кодирование базируется на основной теореме Шеннона
для каналов без шума. Шеннон доказал, что сообщения, составленные из букв некоторого алфавита, можно закодировать так, что среднее число двоичных символов на букву будет сколь угодно близко к энтропии источника этих сообщений, но не меньше этой величины.
где H(x) - энтропия источника; - средняя длина кодового слова; D – «ичность» кода (для двоичного кода D=2, для троичного кода D=3, для восьмеричного кода D=8, для шестнадцатеричного кода D=16).
Кодирование информации
Слайд 149При отсутствии статистической взаимосвязи между буквами конструктивные методы построения эффективных
кодов были даны впервые Шенноном и Фэно.
Алгоритм Шеннона-Фэно: буквы
алфавита сообщений выписываются в таблицу в порядке убывания вероятностей. Затем они разделяются на две группы так, чтобы суммы вероятностей в каждой из групп были по возможности одинаковы. Всем буквам верхней половины в качестве первого символа приписывается 1, а всем нижним 0. Каждая из полученных групп в свою очередь разбивается на две подгруппы с одинаковыми суммарными вероятностями и т. д. Процесс повторяется до тех пор, пока в каждой подгруппе останется по одной букве.
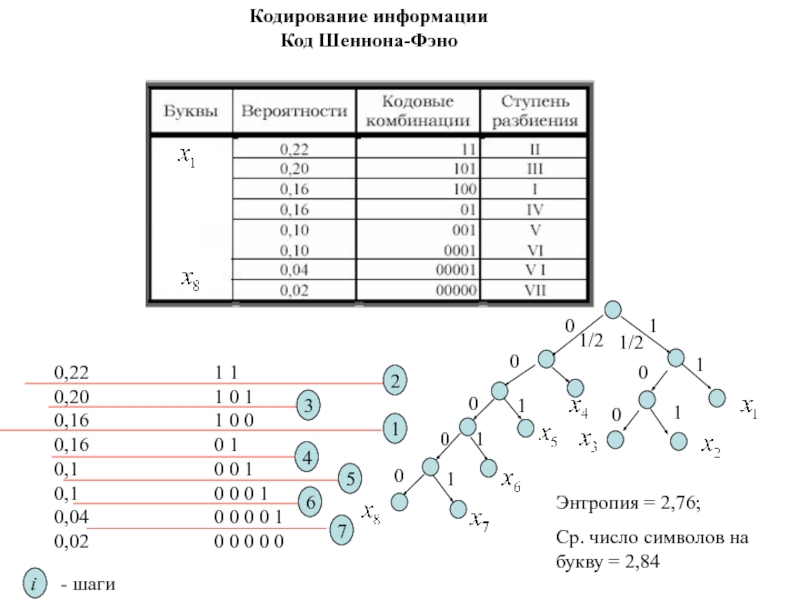
Рассмотрим алфавит из восьми букв. Ясно, что при обычном (без учета статистических характеристик) кодировании для представления каждой буквы требуется три символа. Наибольший эффект сжатия получается в случае, когда вероятности букв - целочисленные отрицательные степени двойки. Среднее число символов на букву в этом случае точно равно энтропии. Убедимся в этом, вычислив энтропию
Кодирование информации Код Шеннона-Фэно
и среднее число символов на букву
где - число символов в кодовой комбинации, соответствующей букве .

Слайд 1501/2
1
1/2
0
1
0
1
0
0
0
0
0
1
1
1
1
Кодирование информации Код Шеннона-Фэно
Слайд 1511/2
1
1/2
0
1
0
0
0,22
0,20
0,16
0,16
0,1
0,1
0,04
0,02
1
1
1
0
0
1
0
0
1 1
1 0 1
1 0 0
0 1
0 0 1
0 0
0 1
0 0 0 0 1
0 0 0 0 0
Энтропия
= 2,76;
Ср. число символов на букву = 2,84
Кодирование информации Код Шеннона-Фэно
1
i
3
4
2
5
6
7
- шаги
Слайд 152Кодирование информации
Код Хаффмана
Методика Шеннона – Фэно не всегда приводит к
однозначному построению кода. Ведь при разбиении на подгруппы можно сделать
большей по вероятности как верхнюю, так и нижнюю подгруппу. От указанного недостатка свободен алгоритм Хаффмана. Она гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву.
Алгоритм Хаффмана для двоичного кода. Буквы алфавита сообщений выписываются в основной столбец в порядке убывания вероятностей. Две последние буквы объединяются в одну вспомогательную букву, которой приписывается суммарная вероятность. Вероятности букв, не участвовавших в объединении, и полученная суммарная вероятность снова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние объединяются. В случае, когда несколько знаков имеют одинаковые вероятности, объединяются те два из них, которые до этого имели наименьшее число объединений. Процесс продолжается до тех пор, пока не получим единственную вспомогательную букву с вероятностью, равной единице.
Коды Хаффмана принадлежат к семейству кодов с переменной длиной кодовых слов. Самый известный код переменной длины – азбука Морзе. Основная идея азбуки Морзе - передавать часто встречающиеся буквы кодовыми словами короткой длины и, наоборот, редко встречающиеся буквы длинными кодовыми словами. Такой способ кодирования называют так же кодированием с минимальной избыточностью.

Слайд 1530,58
1
1
0
1
1
1
0
0
1
0
0
0,42
0,32
0,26
0,16
0,10
0,10
0,06
0,02
0,04
0,16
0,16
0
1
0
0,06
0,10
0,16
0,20
0,32
0,26
Для составления кодовой комбинации, соответствующей данному сообщению, необходимо проследить путь
перехода сообщения по строкам и столбцам таблицы.
Для наглядности строится кодовое
дерево. Из точки, соответствующей вероятности 1, направляются две ветви, причем ветви с большей вероятностью присваивается символ 1, а с меньшей 0. Такое последовательное ветвление продолжаем до тех пор, пока не дойдем до каждой буквы.
Кодирование информации
Код Хаффмана
0,22
0,20
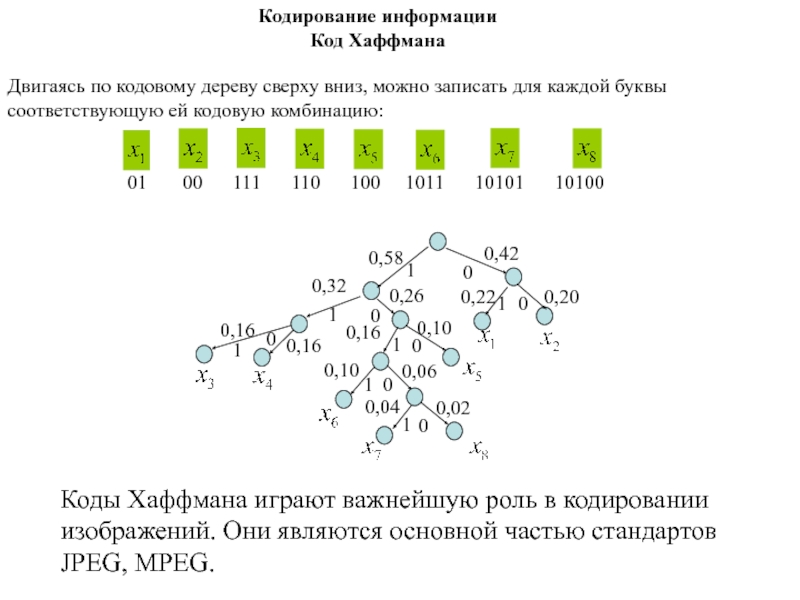
Слайд 154Двигаясь по кодовому дереву сверху вниз, можно записать для каждой
буквы соответствующую ей кодовую комбинацию:
01 00 111 110 100 1011 10101 10100
Кодирование информации
Код Хаффмана
Коды Хаффмана играют важнейшую роль в кодировании изображений. Они являются основной частью стандартов JPEG, MPEG.
0,58
1
1
0
1
1
1
0
0
1
0
0
0,42
0,32
0,26
0,16
0,10
0,10
0,06
0,02
0,04
0,16
0,16
0
1
0
0,22
0,20
Слайд 155Основы теории графов
Теория графов – раздел математики, изучающий графы и
те их обобщения (транспортные сети, гиперграфы и др.), на которые
распространяются некоторые из основных понятий и методов, относящихся к графам.
Одной из первых работ по теории графов была работа Л. Эйлера (1736 г.). Основоположник теории графов – венгерский математик Д. Кёниг, автор первой монографии (1936 г.), в которой графы рассмотрены как абстрактные математические объекты. Значительный вклад в теорию графов внесли советские математики Л.М. Лихтенбаум, А.А. Зыков и В.Г. Визинг.
Слайд 156Основы теории графов
Основные понятия и определения
Совокупность объектов произвольной природы и
отношений между каждой парой этих объектов может быть изображена на
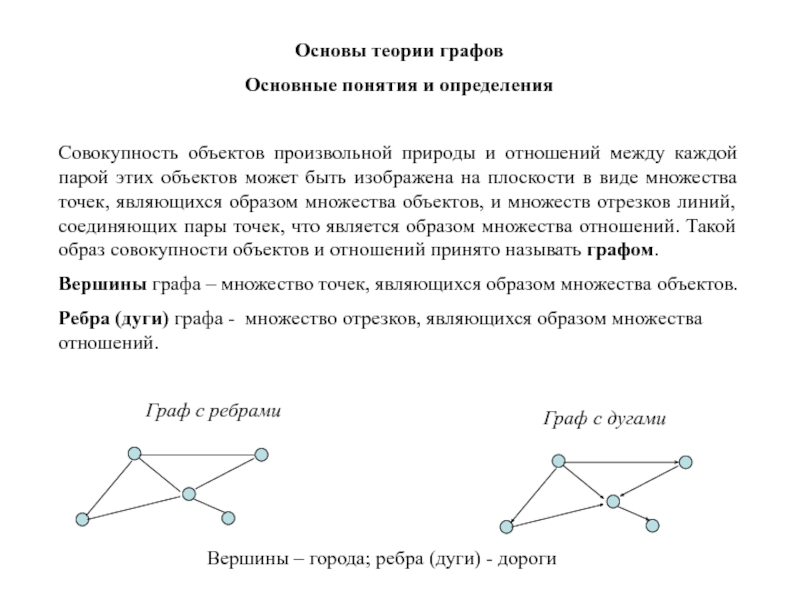
плоскости в виде множества точек, являющихся образом множества объектов, и множеств отрезков линий, соединяющих пары точек, что является образом множества отношений. Такой образ совокупности объектов и отношений принято называть графом.
Вершины графа – множество точек, являющихся образом множества объектов.
Ребра (дуги) графа - множество отрезков, являющихся образом множества отношений.
Граф с ребрами
Граф с дугами
Вершины – города; ребра (дуги) - дороги
Слайд 157Основы теории графов
Основные понятия и определения
Граф может быть задан в
различных формах. Ниже приведена одна из них:
где X –
множество вершин графа G, ; E – множество ребер графа G,
Граф называют неориентированным, если , в этом случае отрезок линии называют ребром.
Граф называют ориентированным, если , в этом случае отрезок линии называют дугой.
Неориентированный граф
Ориентированный граф
Слайд 158Основы теории графов
Основные понятия и определения
Слайд 159Основы теории графов
Основные понятия и определения
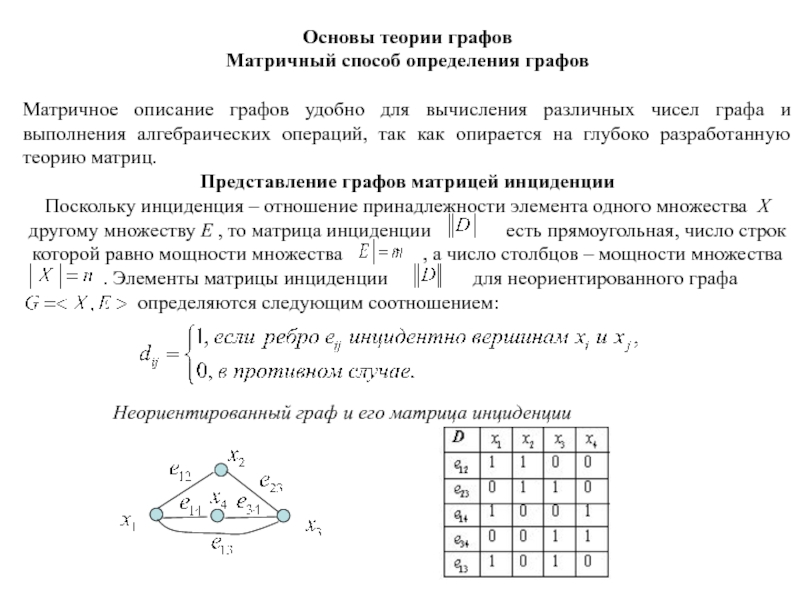
Понятие «инциденции»
Для определения отношения принадлежности
вершин графа ребру или дуге и, наоборот, ребер или дуг
– вершине вводится понятие «инциденции».
Вершина инцидентна ребру или дуге , если она является концевой вершиной данного отрезка линии, а ребро или дуга инцидентна вершине
, если отрезок линии ограничен концевой вершиной .
Следует обратить внимание, что отношение принадлежности, определяющее понятие «инциденции», устанавливает связь между элементами двух разных множеств X и E .
Вершина инцидентна ребрам
Ребро инцидентно вершинам
и т.д.
Слайд 160Основы теории графов
Основные понятия и определения
Понятие валентности
Число вершин, инцидентных ребру
или дуге, всегда равно двум, так как они являются концевыми
вершинами отрезка линии.
Число ребер или дуг, инцидентных вершине , может быть произвольным. Его называют степенью или валентностью вершины и обозначают или
Число дуг для ориентированного графа , исходящих из вершины , называют полустепенью вершины графа и обозначают . Вершину
инцидентную исходящей дуге , называют вершиной-истоком.
Число дуг для ориентированного графа , заходящих в вершину , называют полустепенью вершины графа и обозначают . Вершину
инцидентную заходящей дуге , называют вершиной-стоком.
Слайд 161Основы теории графов
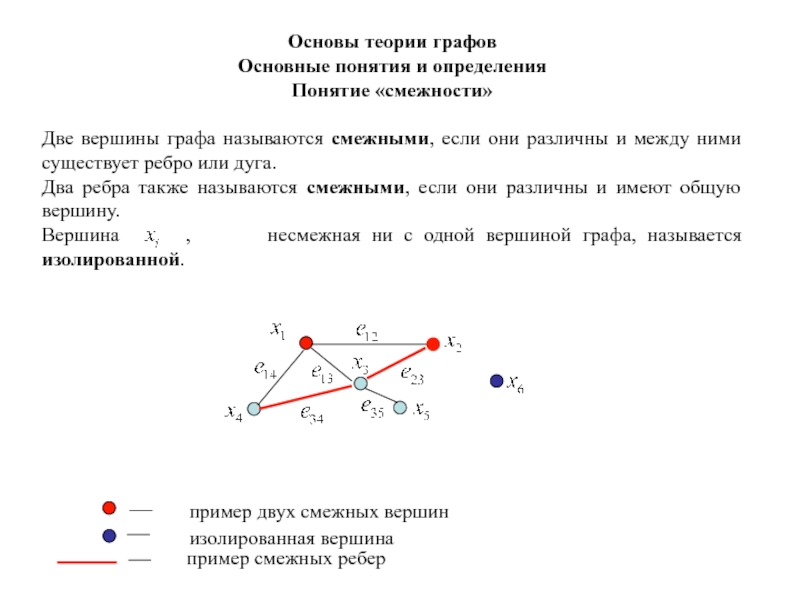
Основные понятия и определения
Понятие «смежности»
Две вершины графа называются
смежными, если они различны и между ними существует ребро или
дуга.
Два ребра также называются смежными, если они различны и имеют общую вершину.
Вершина , несмежная ни с одной вершиной графа, называется изолированной.
пример двух смежных вершин
изолированная вершина
пример смежных ребер
Слайд 162Основы теории графов
Основные понятия и определения
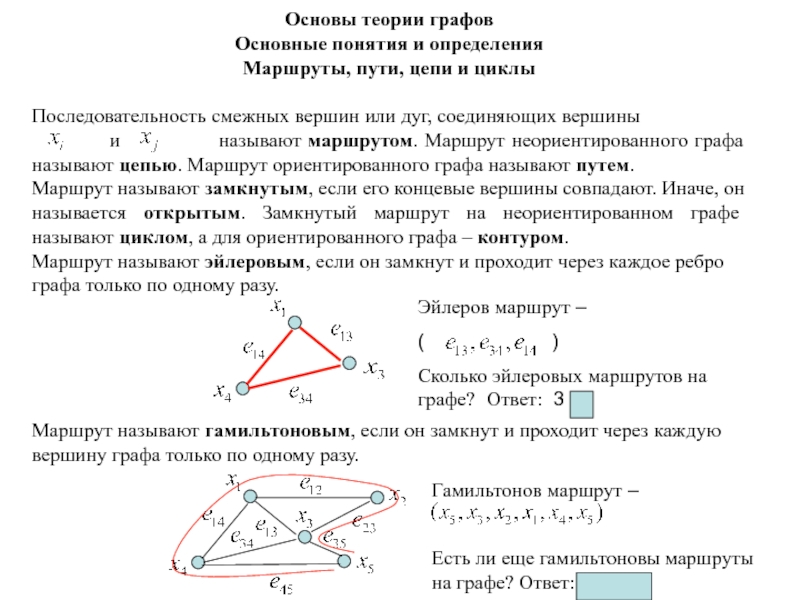
Маршруты, пути, цепи и циклы
Последовательность
смежных вершин или дуг, соединяющих вершины
и называют маршрутом. Маршрут неориентированного графа называют цепью. Маршрут ориентированного графа называют путем.
Маршрут называют замкнутым, если его концевые вершины совпадают. Иначе, он называется открытым. Замкнутый маршрут на неориентированном графе называют циклом, а для ориентированного графа – контуром.
Маршрут называют эйлеровым, если он замкнут и проходит через каждое ребро графа только по одному разу.
Маршрут называют гамильтоновым, если он замкнут и проходит через каждую вершину графа только по одному разу.
Эйлеров маршрут –
( )
Сколько эйлеровых маршрутов на графе? Ответ: 3 .
Гамильтонов маршрут –
Есть ли еще гамильтоновы маршруты на графе? Ответ: да, есть.
Слайд 163Задача о кенигсбергских мостах
Задача о кенигсбергских мостах была сформулирована и
решена Эйлером в 1736 году. План расположения мостов в Кенигсберге
в XV111 веке приведен на рисунке ниже. Задача заключается в том, чтобы пройти каждый мост по одному разу и вернуться в исходную точку. Существует ли такой обход мостов? Решить задачу графически, для чего построить полный граф задачи, в котором каждая часть города — вершина, а каждый мост — ребро, инцидентное вершинам, относящимся к соединяемым им частям суши.
Построим граф G, соответствующий условию задачи. Вершины графа обозначают участки суши, а ребра — городские мосты. Граф G — связный, конечный, неориентированный. Имеет место теорема Эйлера: конечный, неориентированный граф — эйлеров граф, тогда и только тогда, когда он связан и степени всех его вершин — четные. По условию задачи все вершины имеют нечетные степени. Следовательно, в соответствии с теоремой Эйлера обхода мостов не существует.
План расположения мостов в Кенигсберге в ХV111 веке
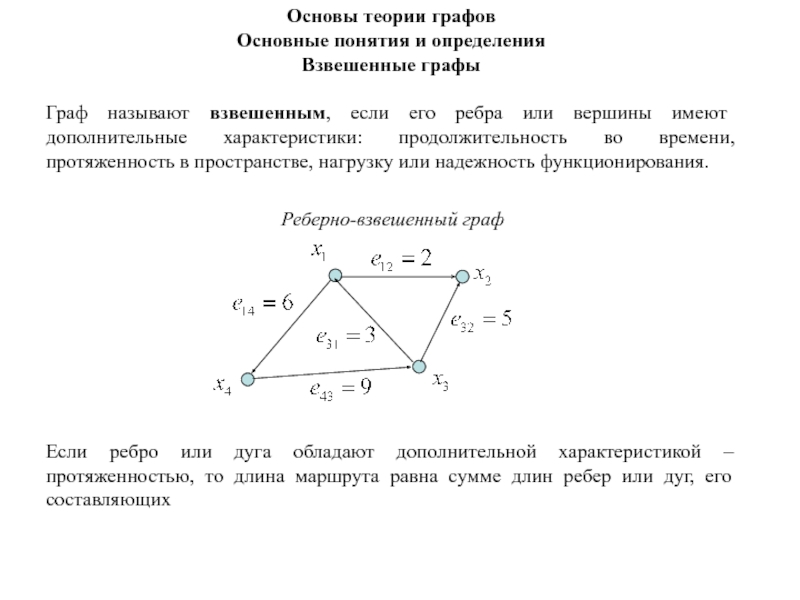
Слайд 164Основы теории графов
Основные понятия и определения
Длина маршрута равна числу смежных
ребер, соединяющих вершины
и
.
Замкнутый маршрут, который содержит только одно ребро или дугу (длина маршрута равна единице), называют петлей.
Граф называют связным, если любые две его вершины можно соединить цепью.
Длина гамильтонова маршрута
равна пяти.
Слайд 165Основы теории графов
Основные понятия и определения
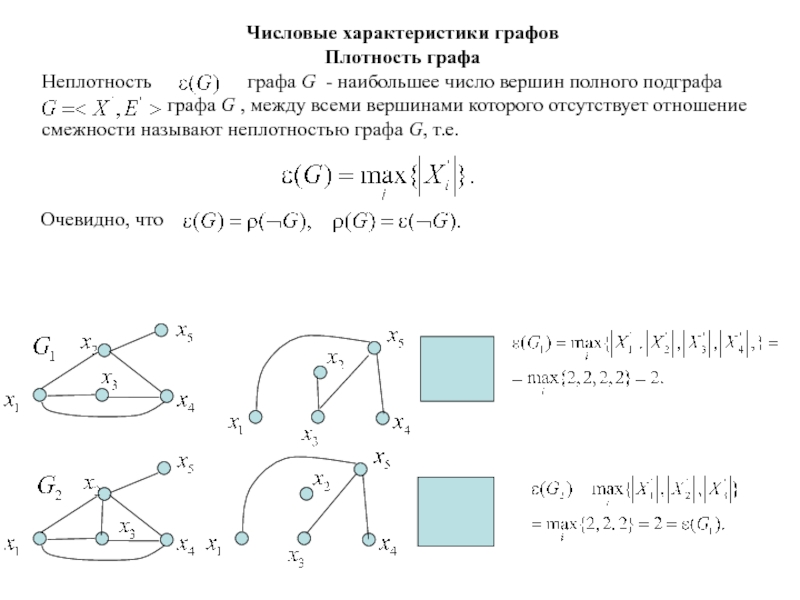
Граф
называют полным, если любые
две его вершины смежны между собой.
Слайд 166Основы теории графов
Основные понятия и определения
Граф
называют пустым,
если любые две его вершины не смежны между собой.
Граф называют дополнительным для графа , если граф имеет те же вершины, что и граф G и содержит только те ребра, которые нужно добавить к графу G , чтобы получить полный граф.
Пустой граф
Полный граф
Слайд 167Основы теории графов
Основные понятия и определения
Дерево, лес
Дерево
Лес
- корень,
- листья.
- ветвь
вершины .
Слайд 168Основы теории графов
Основные понятия и определения
Части, суграфы, подграфы, остовы
Граф
называют частью для графа , т.е.
, если множества его вершин и ребер содержатся в множествах
и соответственно, т.е. и .
Часть графа называют суграфом, если
Подграфом графа с множеством вершин
называется часть, в которой удалены некоторые вершины, причем все ребра, инцидентные этим вершинам, также удалены.
Суграф-дерево связного графа называют его остовом.
Слайд 169Основы теории графов
Основные понятия и определения
Взвешенные графы
Граф называют взвешенным, если
его ребра или вершины имеют дополнительные характеристики: продолжительность во времени,
протяженность в пространстве, нагрузку или надежность функционирования.
Если ребро или дуга обладают дополнительной характеристикой –протяженностью, то длина маршрута равна сумме длин ребер или дуг, его составляющих
Реберно-взвешенный граф
Слайд 170Основы теории графов
Задача коммивояжера
Задача коммивояжера относится к задачам комбинаторного типа
и сводится к поиску в неориентированном графе с весовыми значениями
ребер такого маршрута (простого цикла, включающего все вершины, гамильтонова цикла), у которого сумма весов составляющих его ребер будет минимальной.
В отличие от поиска эйлеровых циклов, проходящих через каждое ребро графа по одному разу, где еще Л. Эйлером получено необходимое и достаточное условие существования цикла, для гамильтоновых циклов такого условия не найдено. Существуют, однако, достаточные условия существования гамильтоновых циклов.
Теорема Дирака. Граф гамильтонов, если степень любой его вершины v удовлетворяет неравенству .
Теорема О.Оре. Граф гамильтонов, если степени любых двух его смежных вершин v и u удовлетворяют неравенству .
В 1859 г. Уильям Гамильтон предложил математическую игру-головоломку с обходом вершин додекаэдра, положив начало одного из самых известных направлений теории графов.
Додекаэдр с n=20
Игрушка с додекаэдром
Додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра.

Слайд 171Одной из самых ранних постановок и решения была задача обхода
доски шахматным конем (Леонард Эйлер, 1757). Найти последовательности ходов, которые
позволяют коню обойти все поля шахматной доски, попадая на каждое поле лишь один раз, и вернуться, в конце концов, на исходное поле. В этом случае роль вершин графа выполняют поля шахматной доски. Предполагается также, что ребра между двумя полями, которые являются «составными частями» хода коня, имеют нулевой вес; все остальные ребра имеют вес равный бесконечности. Оптимальный маршрут имеет нулевой вес и должен быть маршрутом коня.
Основы теории графов
Задача коммивояжера
Слайд 172Задача: определение оптимального обхода 33 городов на карте США
Задача: определение
оптимального обхода одной тысячи случайным образом сгенерированных точек на плоскости.
Основы
теории графов
Задача коммивояжера
Слайд 173Задача: вычертить одной сплошной черной линией без пересечений черно-белое изображение
в ограниченных пределах.
Использовано цифровое изображение (10000 точек). Вершины графа
размещены в соответствии с плотностью изображения (для темных участков плотность городов выше). Точнее – на изображение наложена сетка, клетки которой случайным образом (равномерный закон распределения) заполнены точками-вершинами графа. При этом количество точек соответствует плотности на участке изображения. Строится диаграмма Вороного (диаграмма Вороного (мозаика Вороного, разбиение Вороного, разбиение Дирихле) для конечного множества точек S на плоскости представляет такое разбиение плоскости, при котором каждая область этого разбиения образует множество точек, более близких к одному из элементов множества S, чем к любому другому элементу множества. Названа в честь русского учёного Георгия Феодосьевича Вороного (1868—1908). При этом регион на диаграмме Вороного будет меньше (вершин в нем больше), чем темнее изображение. Решается задача коммивояжера в геометрической постановке, когда для нахождения кратчайшего маршрута на точках одной клетки используются веса ребер графа, как евклидово расстояние между двумя точками. При этом нужно найти точку внутри области (центр области) наиболее близкую ко всем другим точкам области. На второй итерации решается задача построения диаграммы Вороного для множества точек – центров областей.
Основы теории графов
Задача коммивояжера

Слайд 174Основы теории графов
Задача коммивояжера
Сложность и алгоритмы решения
В задачах комбинаторной оптимизации
требуется найти наилучшее из конечного, но очень большого числа возможных
вариантов решений. Если задача характеризуется характерным числом элементов (размерностью задачи), то типичное число решений для выбора растет экспоненциально - или еще скорее - . Согласно формуле Стирлинга для достаточно больших n. Поэтому прямой перебор для поиска решения – неэффективен, время затрачиваемое на поиск растет полиномиально от размерности задачи. Задачи, которые гарантированно допускают нахождение оптимума целевой функции за полиномиальное время относят к классу – Р. Однако есть трудные задачи, для которых оптимальное решение не может быть найдено за полиномиальное время. Для них ограничиваются приближенными (субоптимальными, не сильно отличающихся от экстремальных) решениями. Такие задачи называются NP-полными. Задача коммивояжера – NP-полная задача.
Простейшие методы решения задачи коммивояжера: полный лексический перебор, «жадные алгоритмы» (например, метод ближайшего соседа), метод минимального остовного дерева. На практике используются приближенные (эвристические методы): метод ветвей и границ, экспертные системы, генетические алгоритмы, искусственные нейронные сети и муравьиные алгоритмы.

Слайд 175Основы теории графов
Матричный способ определения графов
Матричное описание графов удобно для
вычисления различных чисел графа и выполнения алгебраических операций, так как
опирается на глубоко разработанную теорию матриц.
Представление графов матрицей инциденции
Поскольку инциденция – отношение принадлежности элемента одного множества X другому множеству E , то матрица инциденции есть прямоугольная, число строк которой равно мощности множества , а число столбцов – мощности множества
. Элементы матрицы инциденции для неориентированного графа
определяются следующим соотношением:
Неориентированный граф и его матрица инциденции
Слайд 176Основы теории графов
Матричный способ определения графов
Элементы матрицы инциденции
для ориентированного графа
определяются следующим соотношением:
Ориентированный граф и его матрица инциденции
Слайд 177Основы теории графов
Матричный способ определения графов
Представление графов матрицей смежности
Поскольку смежность
– это бинарное отношение принадлежности элемента одного множества X другому
множеству E , то матрица смежности есть квадратная матрица, число строки столбцов которой равно мощности множества . Элементы матрицы смежности определяются следующим соотношением:
Неориентированный граф
и его матрица смежности
Ориентированный граф
и его матрица смежности
Слайд 178Основы теории графов
Матричный способ определения графов
Представление графов матрицей весов
Элементы матрицы
весов реберно-взвешенного
графа G определяются соотношением:
Неориентированный, реберно-взвешенный граф и его матрица смежности
Слайд 179Представление графов отображениями
Рассмотрим еще один способ определения графов:
где
- множество вершин графа;
- множество «окрестностей» для каждой из вершин графа.
Пример.
Красным показана окрестность вершины
Слайд 180Матричный способ определения графов
Представление графов матрицей достижимости
Построение и анализ матрицы
достижимости связаны с представлением графа
с помощью множества вершин смежных с вершиной , т.е. «окрестностью» вершины графа.
Вершины из окрестности достижимы их вершины за «один шаг». Поскольку любая вершина связного графа должна быть достижима за , где n – число вершин графа, то справедливо соотношение:
где - множество вершин, достижимых из вершины за p шагов;
множество вершин, достижимых из вершины
за 2,…,p шагов;
Тогда для построения матрицы достижимости удобно воспользоваться матрицей смежности :
где - единичная матрица с единицами на главной диагонали.
Слайд 181Матричный способ определения графов
Представление графов матрицей достижимости
Слайд 182Числовые характеристики графов
Функции, заданные на множестве графов
и принимающие значения на множестве целых чисел, называют характеристиками графа или просто числами графа.
Число компонент связности графа
Если множество Х вершин графа G можно разбить на попарно непересекающиеся непустые множества так, чтобы никакие две вершины из разных подмножеств не были смежны, то связные подграфы называются компонентами графа , а их число - числом компонент связности графа G , которое обозначают .
Двухкомпонентный граф
Слайд 183Числовые характеристики графов
Цикломатическое число
Наименьшее число ребер , удаление которых приводит
к графу без циклов и петель, называют цикломатическим числом и
обозначают .
Цикломатическое число можно определить по формуле:
m - число ребер, n - число вершин, - число компонент связности.
Граф без циклов и петель
Слайд 184Числовые характеристики графов
Хроматическое число графа
Раскраской вершин графа в
цветов называют разбиение множества вершин графа на попарно непересекающиеся
непустые подмножества, состоящие из попарно несмежных вершин, т.е.
Хроматическое число графа G – наименьшее число , при котором никакие две смежные вершины графа не могут быть окрашены в один цвет.
Нахождение хроматического числа трудоемкая задача, имеющая сложный алгоритм и требующая большого объема вычислений.
Оценку можно дать, используя два эвристических правила.
Правило 1 определяет : хроматическое число полного n- вершинного графа равно n ; пустого графа – 1; графа с циклом четной длины – 2; графа с циклом нечетной длины – 3; графа типа дерево – 2.
Правило 2 определяет :
Слайд 185Числовые характеристики графов
Плотность графа
Плотность
графа G - наибольшее число вершин полного
подграфа
графа G , между всеми вершинами которого задано отношение смежности называют плотностью графа G, т.е.
В инфраструктуре современного информационно-индустриального общества сетевые информационные системы занимают одно из ключевых мест.
Плотные графы являются менее «уязвимыми».
Слайд 186Числовые характеристики графов
Плотность графа
Неплотность
графа G - наибольшее число вершин полного
подграфа
графа G , между всеми вершинами которого отсутствует отношение смежности называют неплотностью графа G, т.е.
Очевидно, что
Слайд 187Числовые характеристики графов
Число внутренней устойчивости
Задача о восьми ферзях: требуется так
расставить на шахматной доске наибольшее число ферзей, чтобы они не
атаковали друг друга. Таких ферзей, очевидно, может быть не более восьми.
Обозначим шахматную клетку вершиной графа, а ребром – смежные клетки. Подмножество вершин Х графа G называется независимым (внутренне устойчивым), если никакие две вершины из этого множества не смежны.
Наибольшее по мощности независимое множество называется наибольшим.
К отысканию наибольшего независимого множества вершин графа сводится, например, задача о восьми ферзях
Военные операции, политика
Слайд 188Числовые характеристики графов
Число внутренней устойчивости
Число внутренней устойчивости
графа G – число вершин в наибольшем
независимом множестве графа G
Существует теорема, что для любого графа G верно неравенство
Слайд 189Числовые характеристики графов
Число внешней устойчивости
Задача о пяти ферзях: требуется расставить
на шахматной доске наименьшее число ферзей так, чтобы каждая клетка
доски была под боем.
Очевидно, что вариантов такой расстановки может быть много.
Подмножество вершин графа называется внешне устойчивым, если каждая вершина смежна с некоторой вершиной из .
Внешне устойчивое множество ,
имеющее наименьшую мощность независимое множество называется наименьшим.
К отысканию наименьшего внешне устойчивого множества вершин графа сводится задача о пяти ферзях.
Размещение магазинов на сети населенных пунктов
Слайд 190Числовые характеристики графов
Число внешней устойчивости
Число внешней устойчивости
графа G – наименьшее число вершин смежных
со всеми остальными