Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
СХЕМЫ
Содержание
- 1. СХЕМЫ
- 2. Ключевые словаСхемаГрафСетьДерево
- 3. Схема - это представление объекта в общих, главных чертах с помощью условных обозначений.Схема радиоприёмникаМногообразие схем
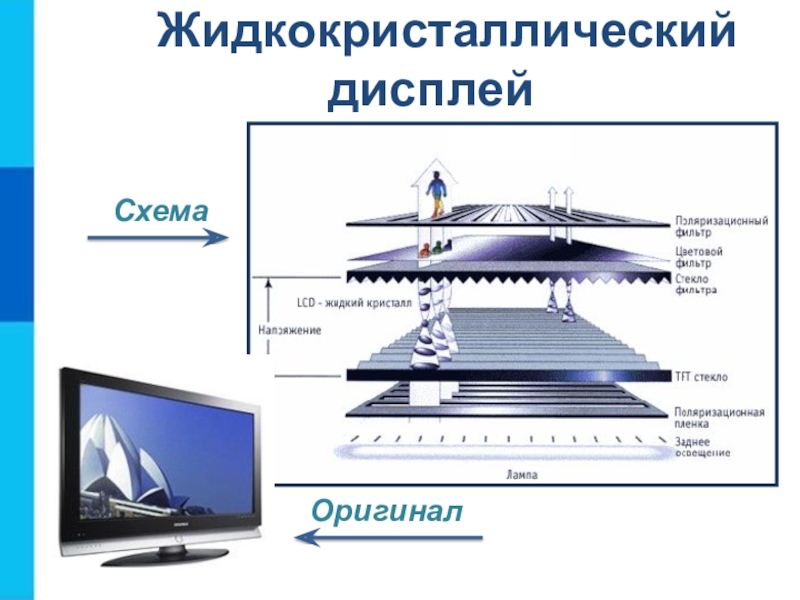
- 4. Жидкокристаллический дисплейСхемаОригинал
- 5. Схема зала театра им. Вахтангова
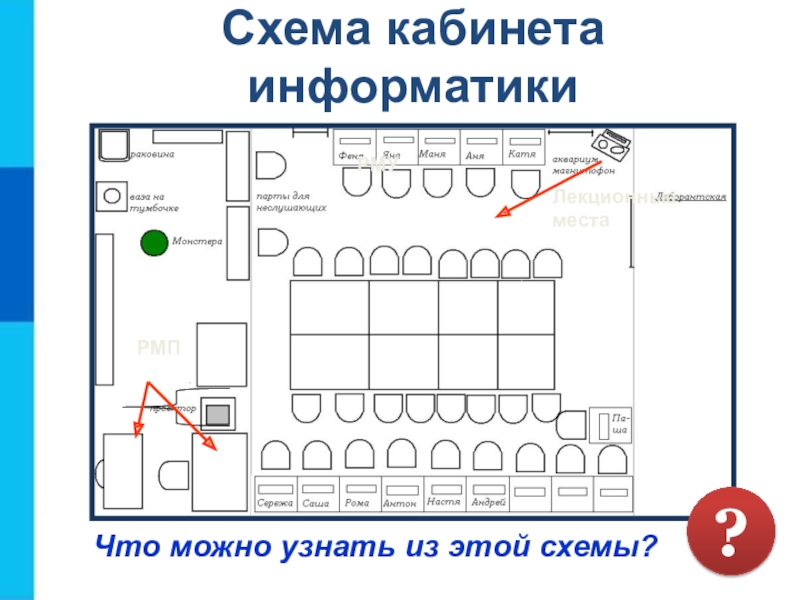
- 6. Схема кабинета информатикиЧто можно узнать из этой схемы?Лекционные местаРМУРМП?
- 7. Схема типовой квартирыВХОДСколько комнат в квартире?Какова площадь
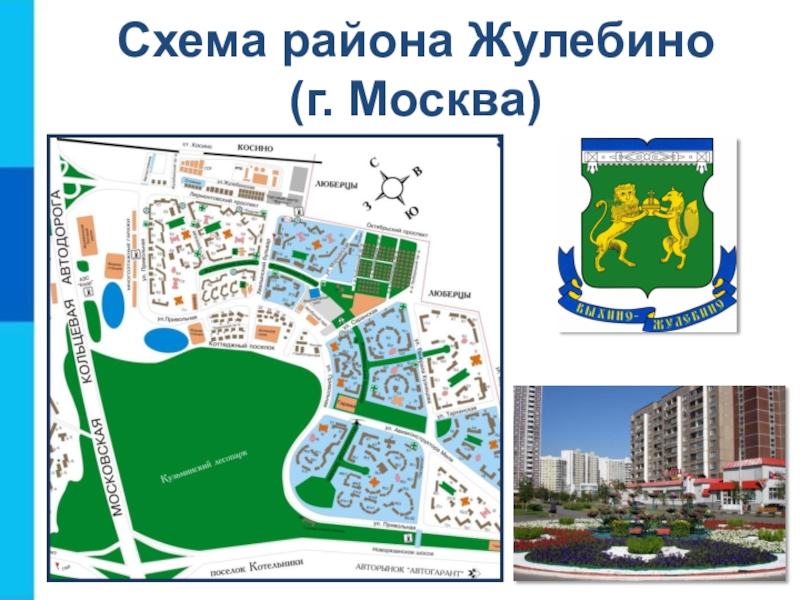
- 8. Схема района Жулебино (г. Москва)
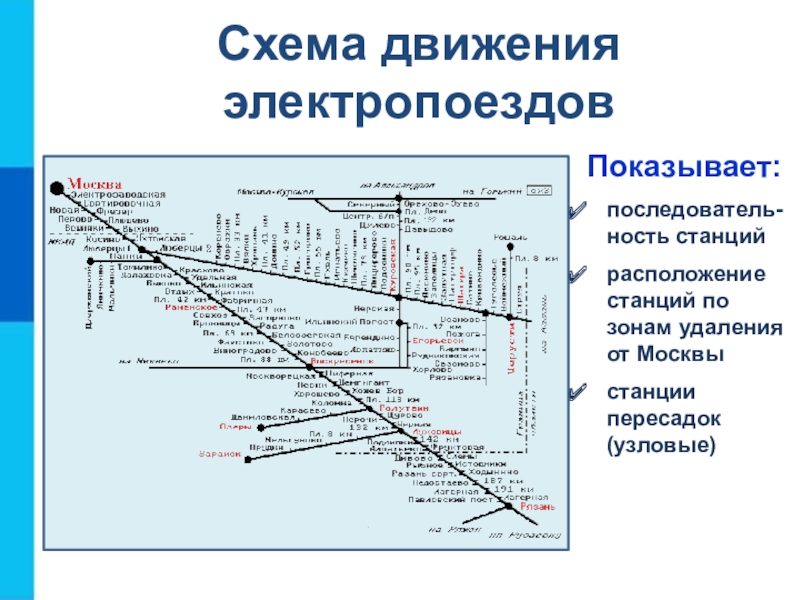
- 9. Схема движения электропоездовПоказывает:последователь-ность станцийрасположение станций по зонам удаления от Москвыстанции пересадок (узловые)
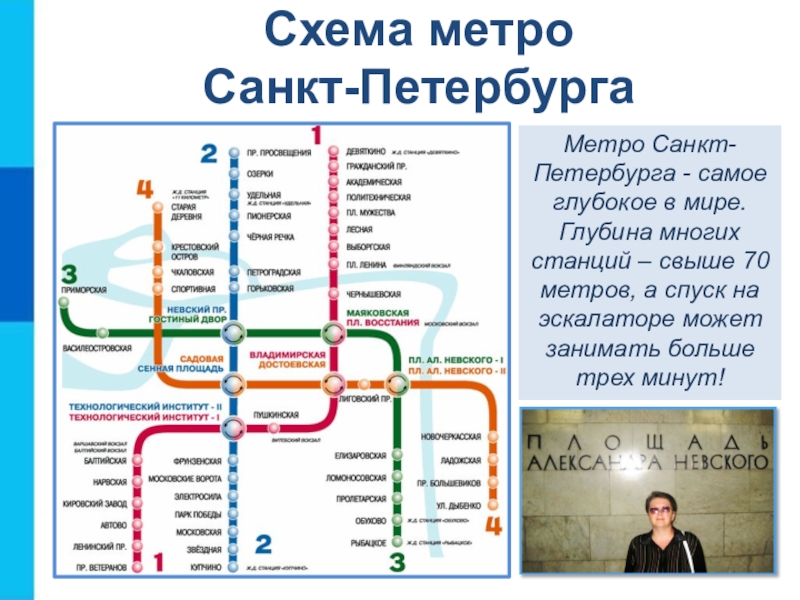
- 10. Схема метро Санкт-ПетербургаМетро Санкт-Петербурга - самое
- 11. Карта центра Санкт-ПетербургаПокажите досто- примечательности, представленные на карте.?
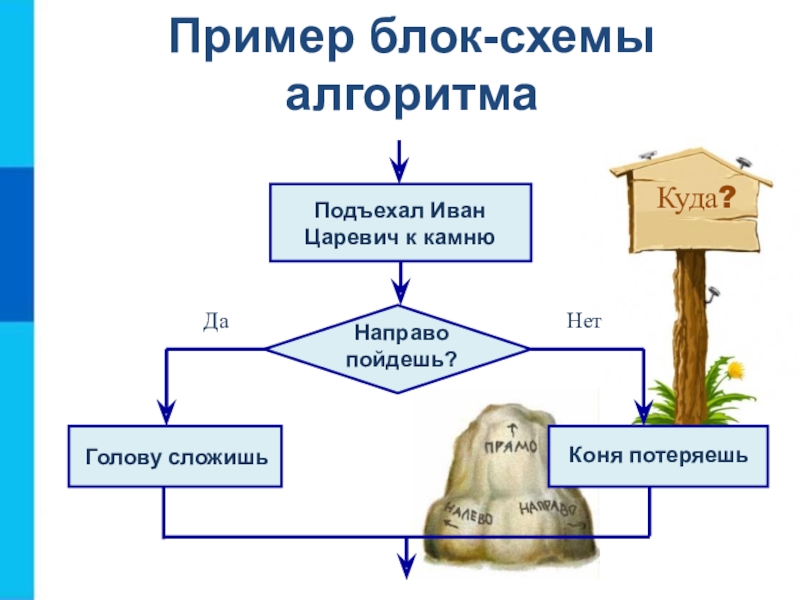
- 12. Пример блок-схемы алгоритма
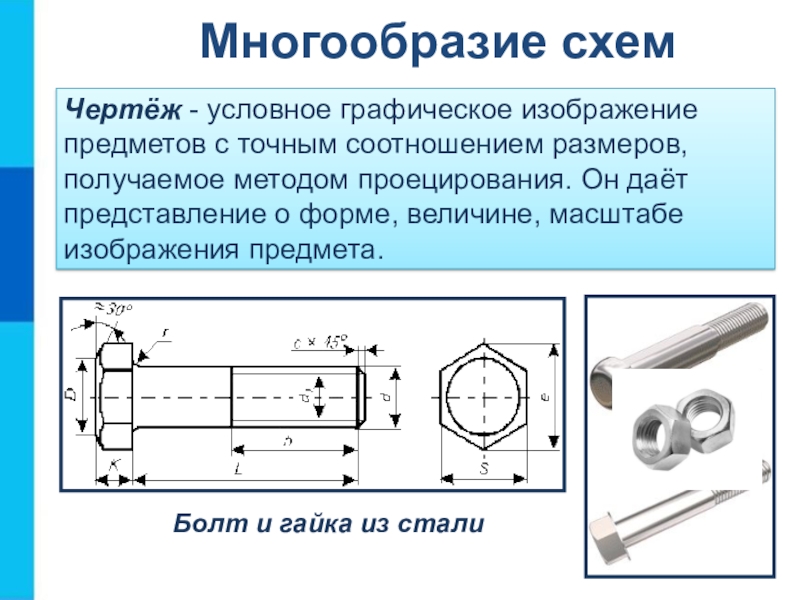
- 13. Чертёж - условное графическое изображение предметов с
- 14. Информационные модели на графахГраф состоит из
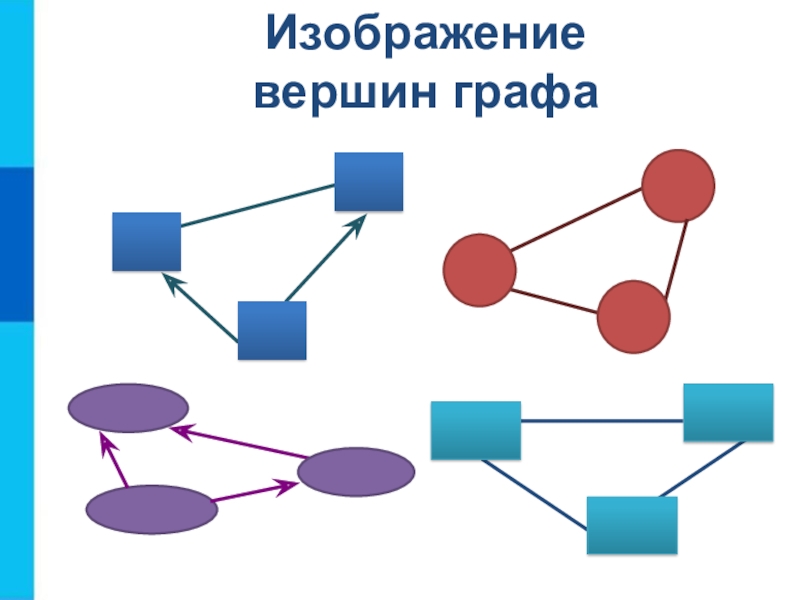
- 15. Изображение вершин графа
- 16. Неориентированный граф С помощью таких графов могут
- 17. Граф отношения «переписываются» Цепь – путь по
- 18. Ориентированный граф Ориентированный граф - граф,
- 19. Взвешенный граф - граф, у которого вершины
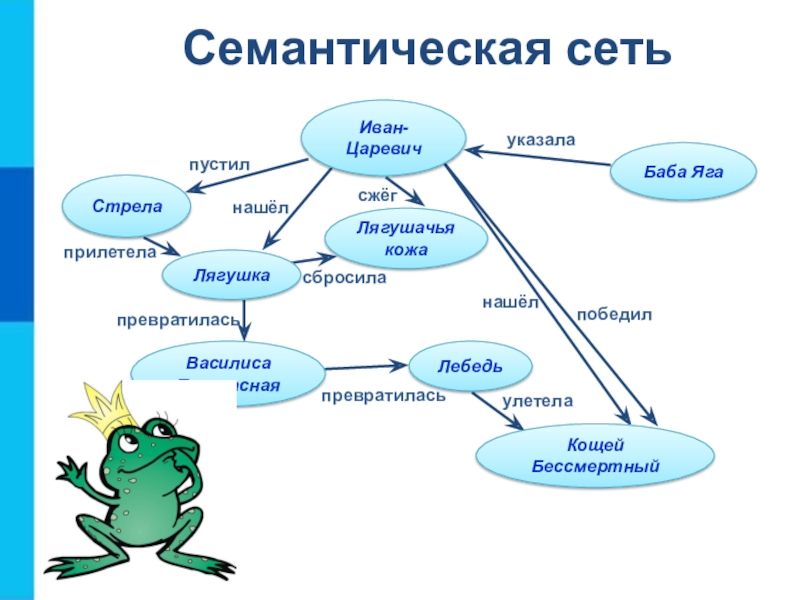
- 20. Семантическая сеть
- 21. Информационные модели на графахИерархия - это расположение
- 22. Классификация компьютеровДерево – граф иерархической структуры.
- 23. ЧемпионФиналистыУчастники ½ финалаУчастники ¼ финалаПервоначальные игрокиУкажите перечисленные
- 24. Файловая структураУкажите корневую вершину, объекты 1-го, 2-го и 3-го уровней.?
- 25. Графы при решении задачСколькими способами можно рассадить
- 26. Решение в виде дереваОНа первый стул посадим
- 27. Самое главноеСхема - это представление объекта в
- 28. Скачать презентанцию
Слайды и текст этой презентации
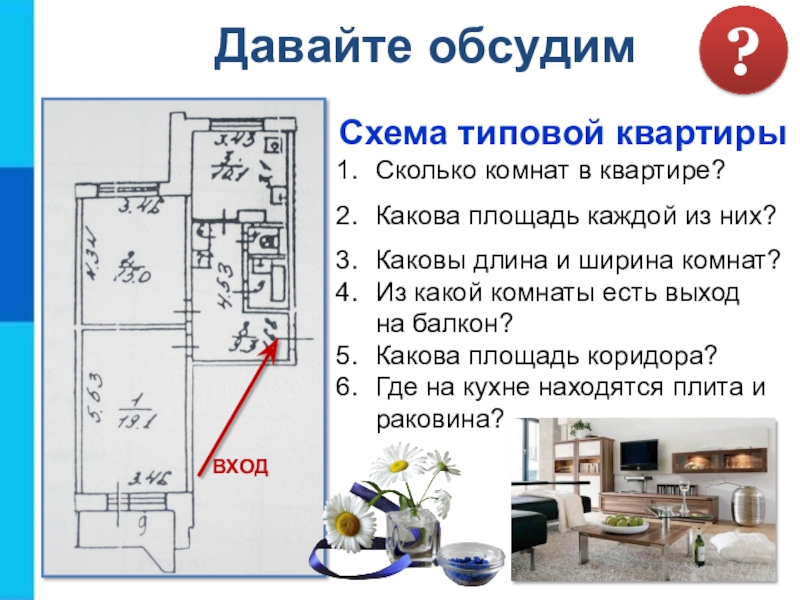
Слайд 7Схема типовой квартиры
ВХОД
Сколько комнат в квартире?
Какова площадь каждой из них?
Каковы
длина и ширина комнат?
Из какой комнаты есть выход
на балкон?
Какова
площадь коридора?Где на кухне находятся плита и раковина?
Давайте обсудим
?
Слайд 9Схема движения электропоездов
Показывает:
последователь-ность станций
расположение станций по зонам удаления
от Москвы
станции
пересадок (узловые)
Слайд 10Схема метро
Санкт-Петербурга
Метро Санкт-Петербурга - самое глубокое в мире. Глубина
многих станций – свыше 70 метров, а спуск на эскалаторе
может занимать больше трех минут!Слайд 13Чертёж - условное графическое изображение предметов с точным соотношением размеров,
получаемое методом проецирования. Он даёт представление о форме, величине, масштабе
изображения предмета.Болт и гайка из стали
Многообразие схем
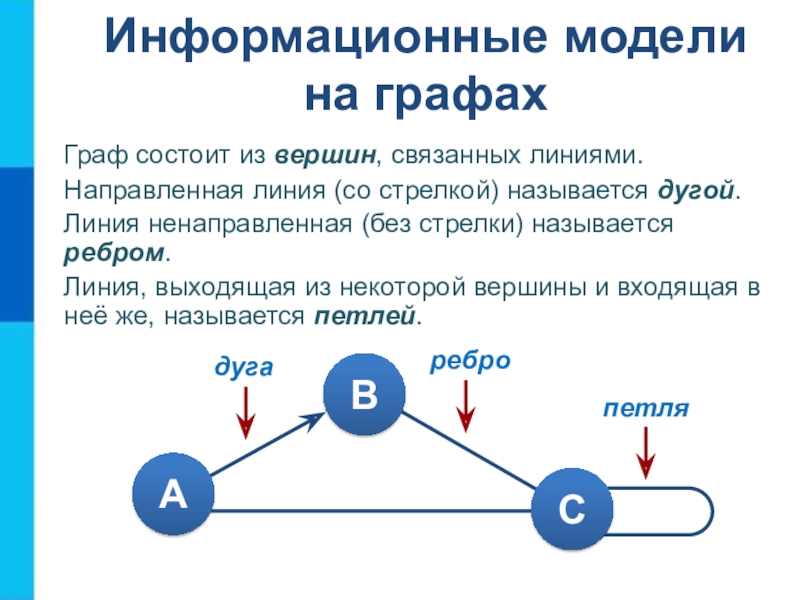
Слайд 14Информационные модели
на графах
Граф состоит из вершин, связанных линиями.
Направленная линия
(со стрелкой) называется дугой.
Линия ненаправленная (без стрелки) называется ребром.
Линия, выходящая
из некоторой вершины и входящая в неё же, называется петлей. петля
ребро
дуга
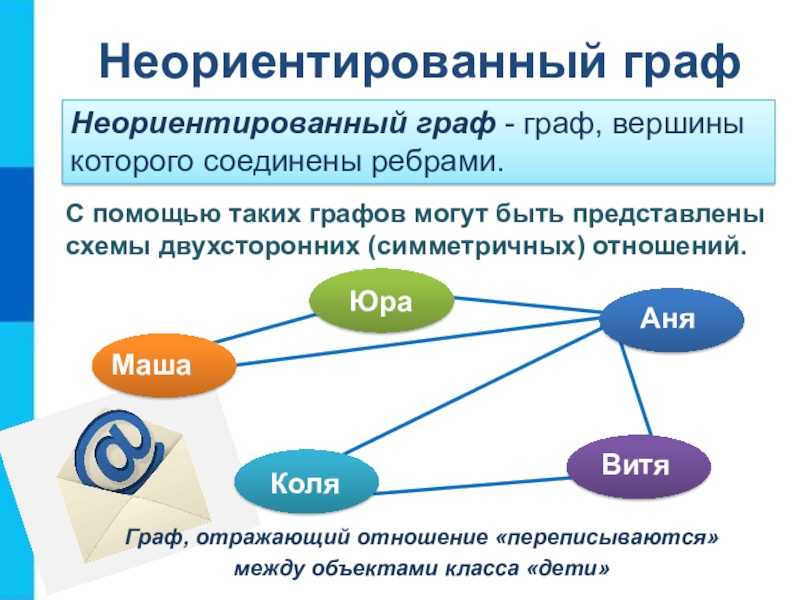
Слайд 16Неориентированный граф
С помощью таких графов могут быть представлены схемы
двухсторонних (симметричных) отношений.
Граф, отражающий отношение «переписываются» между объектами класса «дети»
Неориентированный граф - граф, вершины которого соединены ребрами.
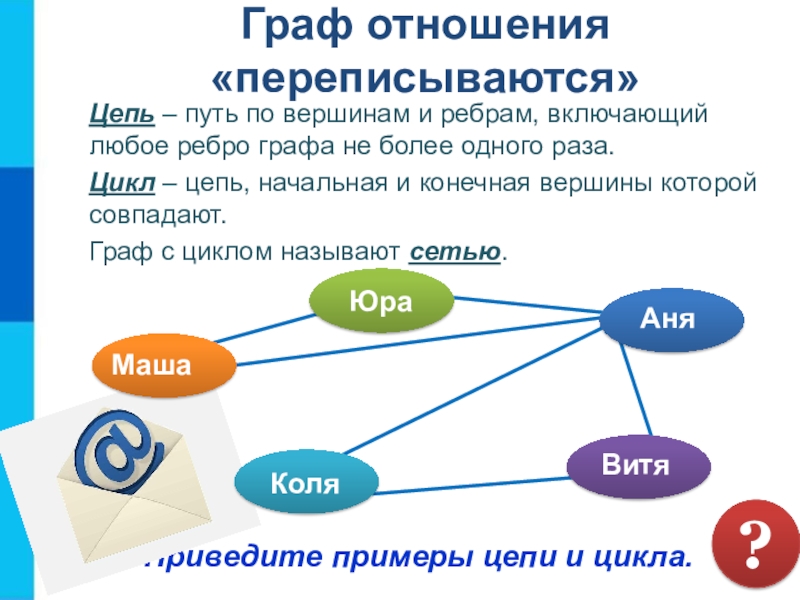
Слайд 17Граф отношения «переписываются»
Цепь – путь по вершинам и ребрам,
включающий любое ребро графа не более одного раза.
Цикл – цепь,
начальная и конечная вершины которой совпадают. Граф с циклом называют сетью.
Приведите примеры цепи и цикла.
?
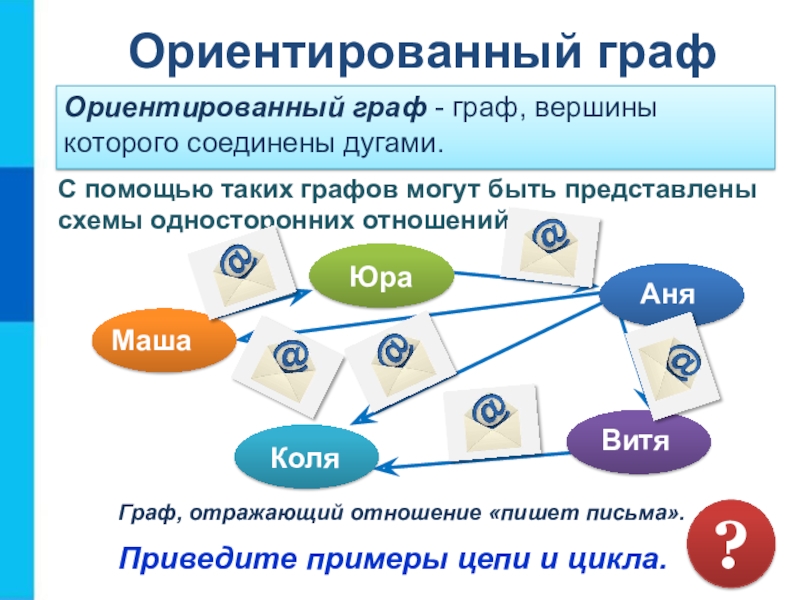
Слайд 18 Ориентированный граф
Ориентированный граф - граф, вершины которого соединены
дугами.
Граф, отражающий отношение «пишет письма».
Приведите примеры цепи и цикла.
?
С помощью таких графов могут быть представлены схемы односторонних отношений.
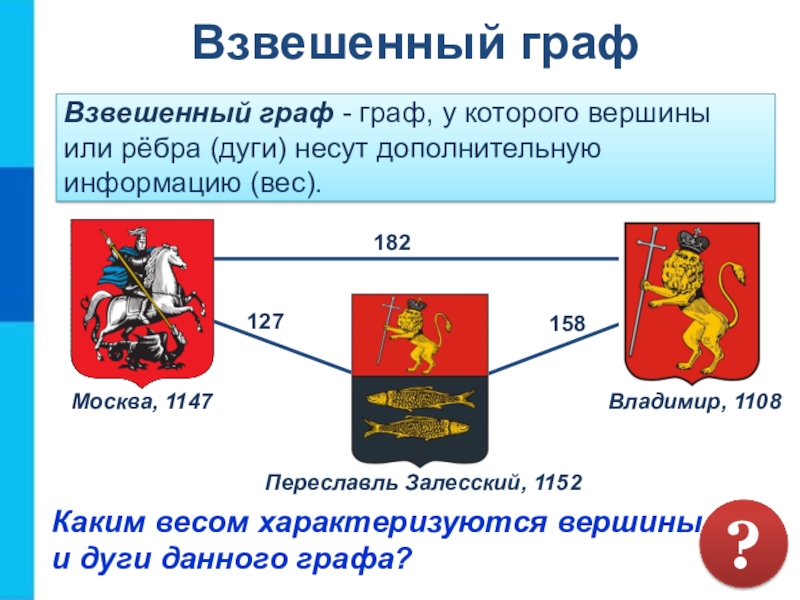
Слайд 19Взвешенный граф - граф, у которого вершины или рёбра (дуги)
несут дополнительную информацию (вес).
Каким весом характеризуются вершины
и дуги данного графа?
?
Взвешенный
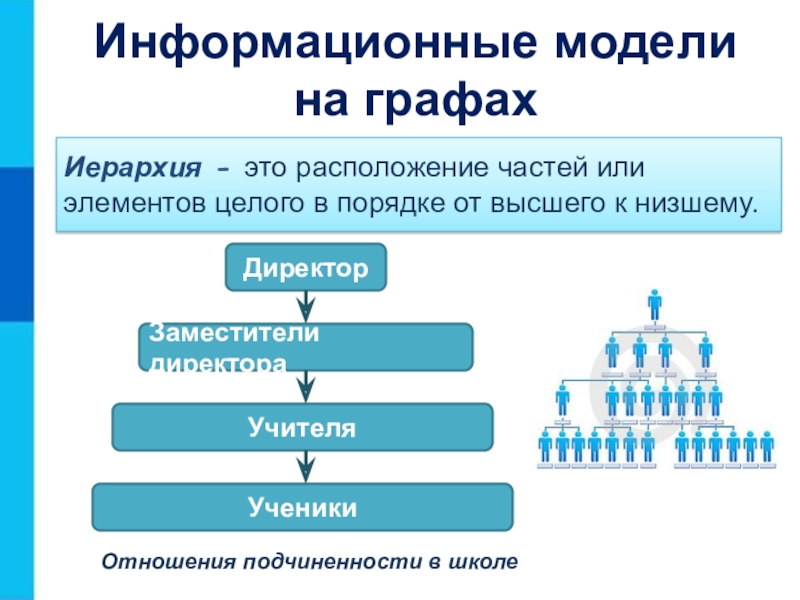
граф Слайд 21Информационные модели на графах
Иерархия - это расположение частей или элементов
целого в порядке от высшего к низшему.
Отношения подчиненности в школе
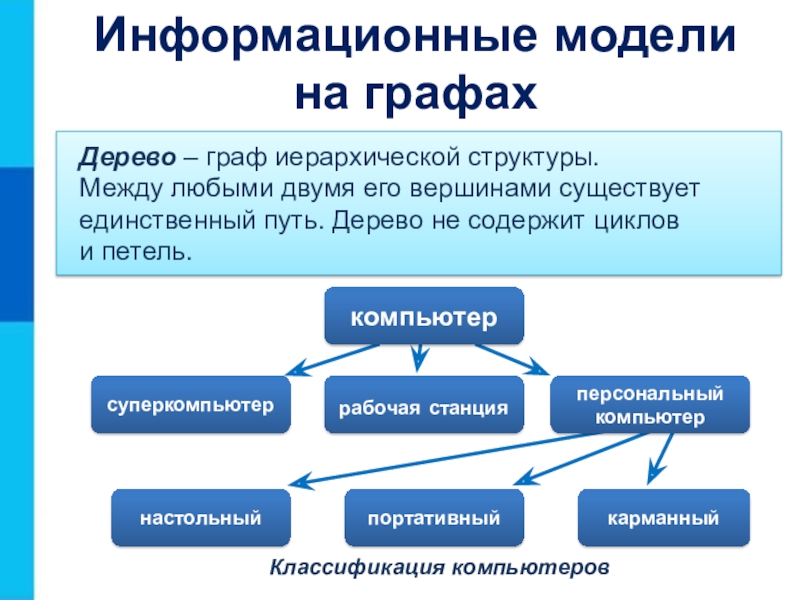
Слайд 22Классификация компьютеров
Дерево – граф иерархической структуры.
Между любыми двумя его
вершинами существует единственный путь. Дерево не содержит циклов
и петель.
Информационные
модели на графахСлайд 23Чемпион
Финалисты
Участники ½ финала
Участники ¼ финала
Первоначальные игроки
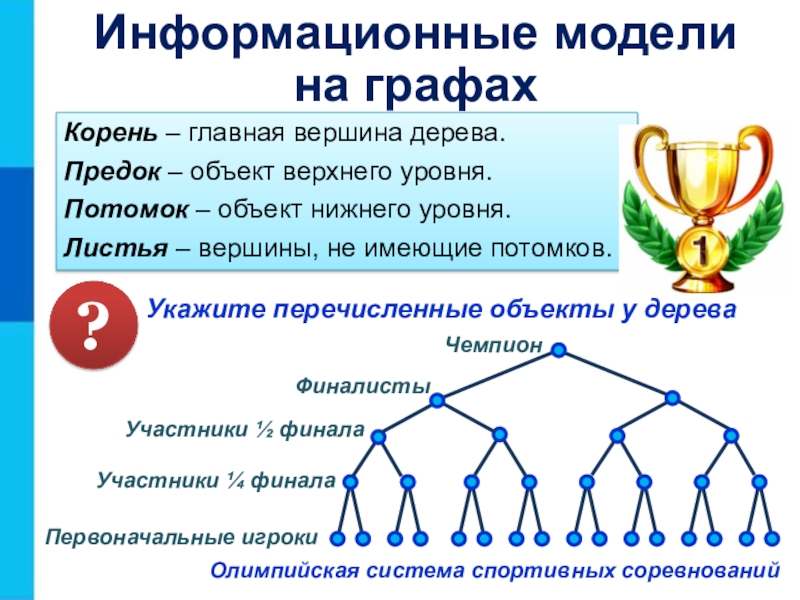
Укажите перечисленные объекты у дерева
Корень
– главная вершина дерева.
Предок – объект верхнего уровня.
Потомок –
объект нижнего уровня.Листья – вершины, не имеющие потомков.
Олимпийская система спортивных соревнований
?
Информационные модели на графах
Слайд 25Графы при решении задач
Сколькими способами можно рассадить
в ряд на
три стула трёх учеников?
Выписать все возможные случаи.
Чтобы выписать все
случаи,
решение можно представить в виде дерева.?
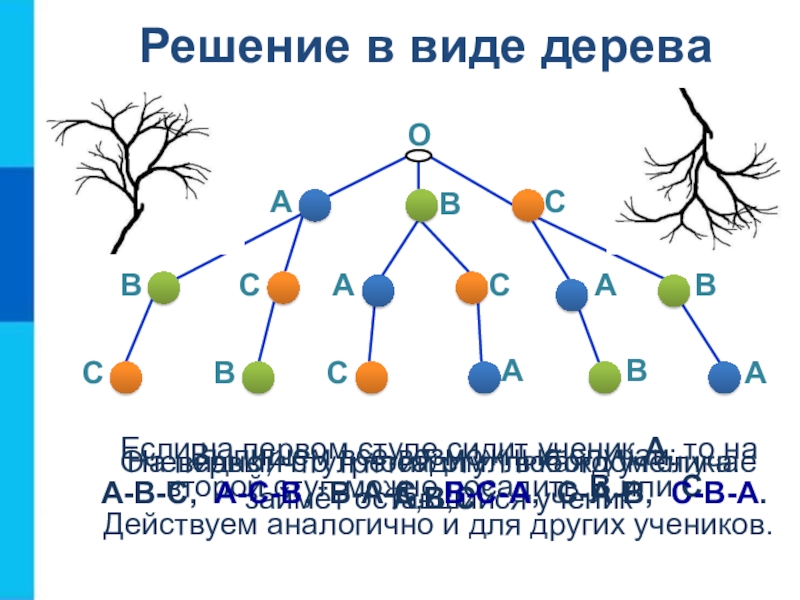
Слайд 26Решение в виде дерева
О
На первый стул посадим любого ученика: А,В,С
Если
на первом стуле сидит ученик А, то на второй стул
можно посадить В или С. Действуем аналогично и для других учеников.Очевидно, что третий стул в каждом случае займёт оставшийся ученик
А
В
С
В
С
А
С
А
В
С
В
С
А
А
В
Выпишем все возможные случаи:
А-В-С, А-С-В, В-А-С, В-С-А, С-А-В, С-В-А.
Слайд 27Самое главное
Схема - это представление объекта в общих, главных чертах
с помощью условных обозначений.
Граф - наглядное средство представления состава
и
структуры системы. Граф состоит из вершин, связанных линиями. Направленная линия называется дугой, ненаправленная – ребром.Иерархия - расположение частей (элементов) целого в порядке от высшего к низшему. Системы, элементы которых находятся в отношениях подчиненности, называются иерархическими системами.
Дерево - граф иерархической системы. Между любыми двумя вершинами дерева существует единственный путь.